壁面切应力是研究水流条件与物质输运、沉积、冲刷以及河道演变相互作用的重要参数，在理论研究和工程实践中都受到了极大的关注。研究表明，泥沙输运率随壁面切应力的增大呈快速非线性增长^[1]。因此，壁面切应力的准确计算对深入了解泥沙输运及河道演变过程非常重要。壁面切应力大小不仅与壁面几何形状和粗糙程度有关，而且受水流流速分布及流态的直接影响^[2]。现有计算方法包括以下3类：解析法、经验公式法、数值模拟法。其中，解析法计算准确，精度高，但实际应用中数据处理复杂，计算量大。据此，有学者提出了简化方法。Kean等^[3]提出Ray-Isovel模型用于顺直河道的壁面切应力计算，之后对该模型不断加以修正，使其适应各种复杂的断面形式以及不同的床面类型。Yang等^[4]利用简化的雷诺方程直接求解顺直光滑矩形河道的壁面切应力。Jin等^[5]利用简化的顺流向涡量方程计算顺直河道壁面切应力的横向分布。Abdorreza等^[6]利用保角映射法求解流体运动方程，从而得到顺直梯形河道内河床和岸坡的平均壁面切应力，计算中还考虑了二次流的影响。以上简化计算方法依然较为繁琐，适用条件也有很大的局限性，能否推广应用于自然河流还有待研究验证。与之相比，经验公式法在实际应用中简单方便，主要有以下8种：阻力平衡法、壁面法、Preston管法、雷诺应力法、雷诺应力外推法、湍动能法、边界层参数法以及水力半径分割法。8种方法适用范围各不相同。阻力平衡法仅适用于均匀流的平均壁面切应力计算。Wilcock^[7]利用壁面法计算简单河道的壁面切应力。Preston管法^[8]是在量纲分析法的基础上建立压强与壁面切应力的经验关系式，沿用至今已有半个世纪之久。McLelland等^[9]利用近壁面的雷诺应力近似得到均匀流的壁面切应力。张小峰等^[10]利用非近壁面雷诺应力外推得到2维明渠非均匀流的床面摩阻流速。Pope等^[11]利用湍动能法计算自然河道的壁面切应力，避免了由测点高度的不准确性带来的误差。Afalimehr等^[12]采用边界层参数法计算砾石河道的壁面切应力，不仅考虑了流动的非均匀性，还剔除了由个别测点的测量误差而带来的计算偏差。杨树清^[13]采用水力半径分割法求解梯形断面的壁面切应力分布，计算中假设水流所含机械能主要通过剪切力场向最近的边界传递，而边界的耗散总是影响邻近水体的运动特征。上述经验公式法虽应用广泛，但其理论欠完善，经验参数的适用条件有待研究确定。数值模拟法是以计算机为载体，通过添加湍流模型实现流体运动方程的封闭求解，适用于各种复杂的3维流体^[14-15]，具有假设限制少、应用方便、适用范围广等特点。此外，数值模拟的“探测”并不干扰流动，流场更贴近真实情况。上述计算方法多局限于顺直和微弯河道壁面切应力的研究，而对于急弯河道，水流流态复杂，水流受重力和离心力的双重作用，水面横比降大，并伴随横向环流^[16]，选择合理的二次流系数才能更好地模拟壁面切应力的分布^[17]，尤其是针对窄深式明渠，受侧壁影响大，存在较强二次流时，简单的对数公式已不能反映紊流流速分布^[18]。此外，主流偏移冲击凹岸，凹岸附近出现明显的沉降流，其壁面切应力不仅与重力 (能坡) 有关，而且受动量重分布 (纵向流速重分布) 以及湍流的影响^[19]，各种计算方法的适用性有待进一步研究。

本文选取180°急弯宽浅式水槽，研究急弯条件下缓流的典型特征，对比分析现有经验公式和数值模拟方法，得到适合急弯河道壁面切应力计算的有效方法；并进一步分析急弯河道内河床及岸坡壁面切应力的分布及变化规律。

试验在如图 1所示的180°弯道水槽中展开。水槽底坡降为0.1%，上、下游顺直段分别长16 m、10 m。水槽断面形状为梯形，几何尺寸如图 1所示。弯道段平均弯曲半径R=2.186 m，平均宽度B=0.773 m，R/B < 3，属急弯河道^[20]。水槽进口设有流量调节阀门，出口设置尾门控制水位。试验控制断面水深H=0.14 m，B/H=5.5>5，为宽浅式水槽。过流量设定为50 L/s，断面平均流速为0.465 m/s，Fr=0.40，属缓流。

图1(Fig. 1)

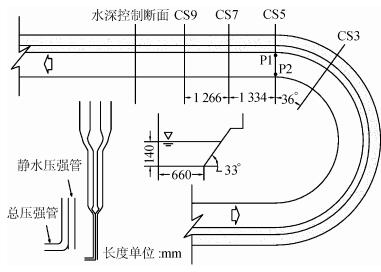图1 180°急弯河道概化模型及Preston管示意图 Fig. 1 Generalized model of 180°sharply-curved channel and Preston tube

ADV流速仪和Preston管监测弯道水流的3维流速和压强。ADV流速仪主要由测量探头、信号调理、信号处理这3部分组成。测量时，将探头完全淹没于水中，由探头发射超声波，遇到控制体后反射信号，之后被接收探头接收，运用声学多普勒原理对信号加以处理得到控制体的3维流速。其中，控制体距离发射探头约为5 cm，这样基本可以消除探头对流场的干扰，同时也使得水面以下5 cm范围内的水流流速无法测量。ADV流速仪在边壁及底壁测量中均能获得理想的数据，得到了广泛的应用。

自制Preston管主要由两部分组成:一根用于总压强测量的弯管与一根用于静水压强测量的直管，如图 1所示。测量时，将Preston管沿铅垂方向伸入水中，使弯管的弯段部分紧贴壁面，保持弯管出口方向与水流方向平行，待两管水头稳定后，利用比压计读取水头差ΔH。自制Preston管在使用之前，需对其进行流速率定，在水槽顺直段内采用ADV流速仪与Preston管进行对比测量，结果如图 2所示，拟合得到的流速线性关系如式 (1) 所示。

图2(Fig. 2)

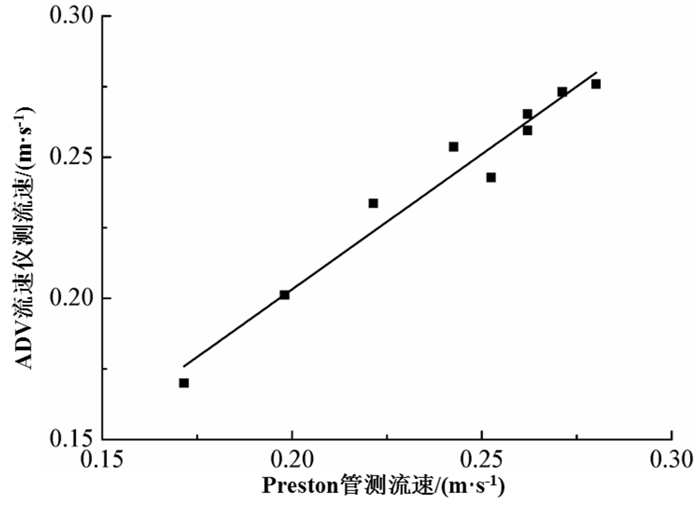图2 ADV和Preston管流速量测对比图 Fig. 2 Comparison of velocity measured between ADV and Preston tube

其中，U_ADV是ADV流速仪测得的流速，U_P是Preston管测得的流速。

试验共设置4个测量断面 (CS3、CS5、CS7、CS9)，其位置如图 1所示。每个断面河床上横向布置7条垂直测线，每条测线布置15个测点，测点间距1 cm，并在近壁面适当加密，间距为0.1~0.2 cm。岸坡上布置3条垂直测线，每条测线根据水深确定测点个数，测点间距为1 cm。

ADV流速仪监测3维瞬时流速，采样频率为200 Hz，采样时间为40 s。u_i、v_i、w_i分别为水流纵向、横向、垂向瞬时流速。以纵向流速为例，时均流速$u=\frac{1}{200\times 40}\sum{{{u}_{i}}}$，脉动流速u′=u_i-u。水流流经弯道做曲线运动，水面形态和水流结构都会出现调整和变化，呈现出典型的弯道水流特征，主要表现为纵向流速重新分布和出现横向环流。横断面纵向流速分布如图 3所示，水流流经弯道时，在离心力作用下，主流位置发生变化，从凸岸向凹岸转移。此外，在凹岸岸坡处，主流位置在垂向上被抬升，这是由于在岸坡作用下水深减小，而主流中心位置与水深的变化趋势相反。水流从CS3流向CS5时，主流流速有所下降，这是由于出口处弯道对水流的约束作用有所减缓。水流进入下游顺直段后，水流流态不断调整，断面流速分布逐渐均匀。这与前人的研究成果^[21]一致。

图3(Fig. 3)

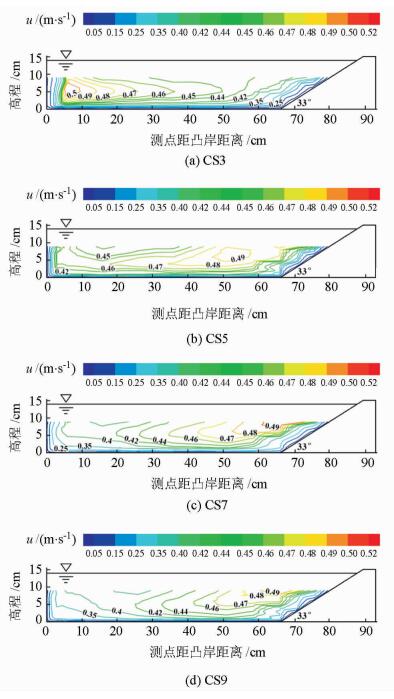图3 横断面纵向流速等值线 Fig. 3 Contour of longitudinal velocity in cross sections

横断面流线及横向流速如图 4所示，水流出现横向环流现象，表层水流由凸岸流向凹岸，底层水流由凹岸流向凸岸。这是由于水流流经弯道时，在离心力作用下，形成水面横比降，弯道断面出现横向压力差，这种沿垂线均匀分布的压力差和非均匀分布的离心力，使横断面内形成螺旋流。水流由CS3流向CS7时，螺旋流中心位置逐渐向水面偏移，这可能是受到主流偏移的影响。水流由弯段进入下游顺直段的过程中，水流的横向流速不断减小，流线的曲率降低，环流作用逐渐减弱。

图4(Fig. 4)

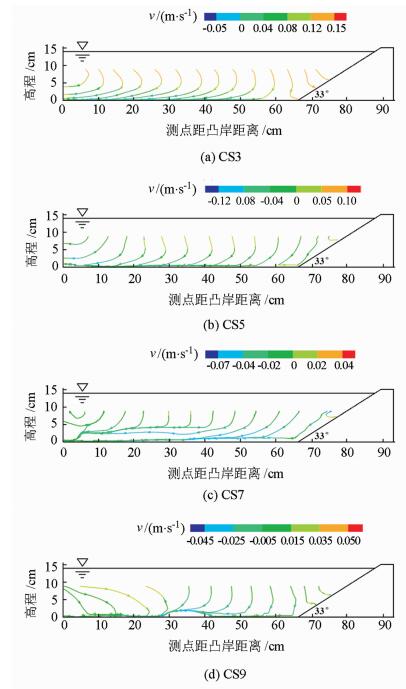图4 横断面流线及横向流速分布 Fig. 4 Streamline and contour of transverse velocity in cross sections

湍动能比$\frac{{{K}^{'}}}{\left( {{U}^{2}}/2 \right)}$分布如图 5所示，其中，${{K}^{'}}=\left[\overline{{{u}^{'}}{{\left( t \right)}^{2}}}+\overline{{{v}^{'}}{{\left( t \right)}^{2}}}+\overline{{{w}^{'}}{{\left( t \right)}^{2}}} \right]/2$为湍动能，U为断面平均流速。受梯形断面形态的影响，最大湍动能均位于凹岸坡脚附近。水流进入弯道出口断面CS5，断面最大湍动能值达到最大，进入顺直段后，断面最大湍动能逐渐减小，这与环流作用变化相似。

图5(Fig. 5)

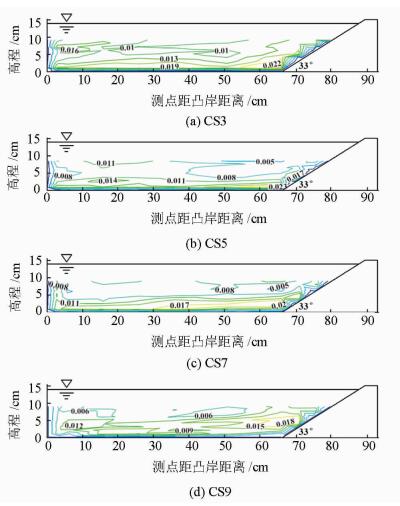图5 横断面湍动能比等值线 Fig. 5 Contour of normalized turbulence kinetic energy in cross sections

Preston管测量得到的水头差分布如图 6所示，与弯道内水流的流速分布相似，水头差的分布也具有明显的非均匀性。断面内水头差的横向分布各不相同，弯道内CS3表现为凸岸附近大于凹岸岸坡附近；弯道出口CS5表现为河床中部大于两岸附近；下游顺直段CS7、CS9都表现为凸岸附近远小于凹岸岸坡附近。最大水头差的位置由凸岸逐渐转移至凹岸。

图6(Fig. 6)

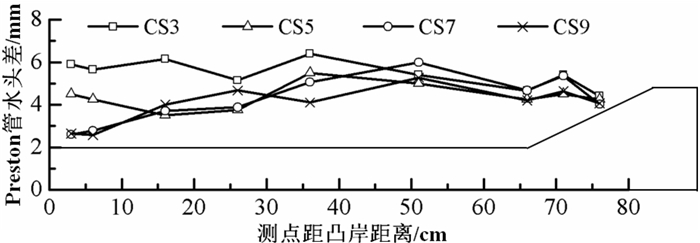图6 Preston管水头差分布 Fig. 6 Distribution of water head difference measured by Preston tube

针对上述水流观测结果，选用以下4种经验公式法计算水槽壁面切应力，对比分析经验公式法与3维数学模型计算结果，寻求合适的急弯河道壁面切应力计算方法。

1954年Preston^[8]以壁面率为基础，应用量纲分析法建立压强与摩阻流速的相互关系如式 (2) 所示，利用自制Preston管测量的压强差ΔP(=ρgΔH) 推求壁面切应力τ₀，不仅适用于光滑壁面，对粗糙壁面也同样适用^[22]。

采用Patel的三方程率定曲线进行计算，如式 (3) 所示。

其中，${{X}^{*}}=\lg \left( \frac{\Delta P{{d}^{2}}}{4\rho {{\nu }^{2}}} \right), {{Y}^{*}}=\lg \left( \frac{{{\tau }_{0}}{{d}^{2}}}{4\rho {{\nu }^{2}}} \right), d$为Preston管的外径，ν为水的运动黏度。

1987年Schlicting首次将壁面法应用于壁面切应力的计算中，计算公式如式 (4) 所示：

其中：z为测点距壁面的铅垂高度；u(z) 为该测点的纵向时均流速；κ为卡门常数，一般情况下κ取0.40；z₀为特征粗糙度，目前还无法准确估计^[7]。该方法利用一系列测量的 (u, z) 值进行对数拟合得到壁面摩阻流速u_*及相应的z₀，有效地排除了个别流速点的测量误差。仅需进行时均流速的测量，计算方便快捷，适用于边界层充分发展的流动。应用于非均匀流时，需确保其非均匀性产生的压力梯度对近壁区域无明显影响。此外，对于壁面相对糙率较大的流动，壁面法也是无法适用的^[23]。

1983年Soulsby提出通过近壁面总动能计算壁面切应力，计算公式如式 (5) 所示，适用于各种流动条件，并广泛应用于海洋学。

其中，u′、v′、w′分别为测点纵向、横向、垂向三方向上的脉动流速，c为经验系数。应用于自然河道时，测点常位于z=0.1h处, c取0.19^[11]。

1975年Hinze提出通过边界层参数计算壁面切应力，计算公式如式 (6) 所示，将流体的非均匀性影响纳入壁面切应力的计算中，以更好地适应各种复杂的水流条件^[12]。此外，边界层各参数之间的关系以及经验系数的适用条件还有待进一步研究。

其中:边界层位移${{\delta }_{*}}=\int\limits_{0}^{h}{\left( 1-\frac{u}{{{u}_{\max }}} \right)\text{d}y}$，表示边界层作用下外部流线的垂向位移；动量厚度$\theta =\int\limits_{0}^{h}{\frac{u}{{{u}_{\max }}}\left( 1-\frac{u}{{{u}_{\max }}} \right)\text{d}y}$，表示边界层作用下的动量损失；u为纵向时均流速; u_max为垂线上最大纵向时均流速值; C为经验参数，取为4.4^[12]。

Fluent采用有限体积法对3维流体运动方程进行离散求解，从而得到壁面切应力。针对流体流动特点, Fluent提供了丰富的湍流模型，主要有Spalart-Allmaras模型、k-ε模型、k-ω模型以及雷诺压力模型。各种湍流模型适用条件不同，对计算机资源的要求也差别较大。

k-ε模型应用最为广泛，其计算收敛性和精确性都能很好地满足计算要求。选择更加适用于复杂剪切流动、螺旋流、二次流以及分离流的RNG k-ε模型进行计算，基本方程如下：

其中：k为湍动能；ε为湍动能耗散率；μ_eff为有效黏性系数，考虑了雷诺数及漩涡尺度对湍流的影响，使之不仅适用于高雷诺数流动，对低雷诺数流动以及近壁面流动也同样适用；α_k和α_ε分别为湍动能及其耗散率的Prandtl倒数，RNG理论为湍流Prandtl数提供了解析公式；G_k为时均流速梯度产生的湍动能；G_b为浮力产生的湍动能。

高雷诺数的湍流方程无法直接求解近壁面区域，通常可改进湍流模型直接求解或采用壁面函数法模拟壁面对湍流的影响。近壁面区域可分为3层：黏性底层、完全湍流层 (对数层) 以及位于两者之间的过渡层。其中，过渡层在明渠中占有的部分很少，没有明确的流速分布公式。壁面函数法即采用半经验公式来求解过渡层。对于大多数高雷诺数流动，采用壁面法可减少计算量并具有一定的精度，因此得到了广泛的应用。Thorsten等^[15]曾分别采用细网格的大涡模拟法和基于壁面函数法求解的k-ε湍流模型对180°弯道的壁面切应力进行计算，结果表明两种方法的计算值吻合良好。因此，采用包含压力梯度的非平衡壁面函数法对近壁面区域进行求解。

计算采用VOF模型模拟自由液面。该模型通过计算每一个网格内目标流体体积与网格体积的比值，从而实现对运动界面的追踪，广泛应用于自由面流动、液体中气泡流动、溃坝水流等气液两相流问题。

计算范围包括弯道段和上、下游顺直段2.5 m、4 m，共14.5 m。计算段进出口边界条件同试验条件；水槽边界为无滑移边界。采用结构化网格进行划分，并在近壁面适当加密。近壁面区域采用壁面函数法求解，第1层网格应设置在对数层，即11.25 < y⁺ < 300，其中，y⁺=yu_*ν^-1，取y⁺=15，划分后的总网格数为90×50×800=3.6×10⁶，网格大小5 mm×5 mm×10 mm，边壁附近网格大小0.4 mm×0.4 mm×10 mm。急弯河道概化模型网格分布如图 7所示。初始时，水槽内水深为0.14 m。

图7(Fig. 7)

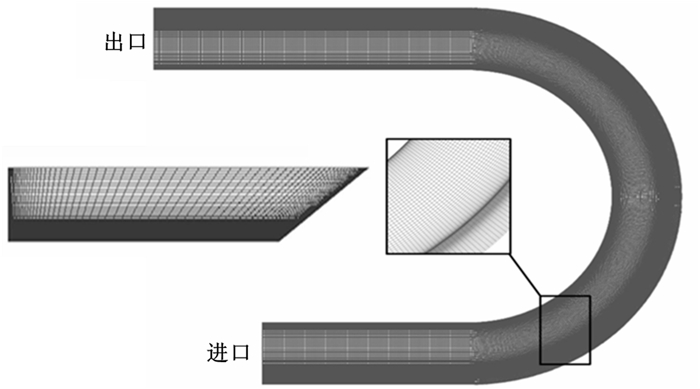图7 急弯河道概化模型网格分布 Fig. 7 Grid distribution of the generalized model

为确保壁面切应力计算的准确性，需对RNGk-ε模型进行验证。选取弯道出口CS5的纵向及横向流速模型计算值与测量值进行对比，如图 8所示。

图8(Fig. 8)

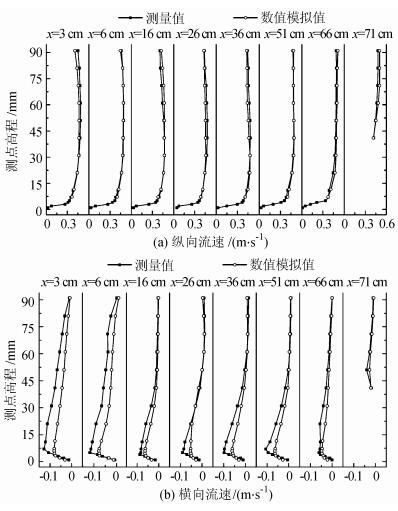图8 横断面CS5纵向及横向流速对比验证 Fig. 8 Verification of longitudinal and transverse velocity calculated by numerical simulation in CS5

其中，x为该测线距凸岸边壁的距离。由图 8可以看出：测点纵向流速值吻合良好；横向流速在各测线上分布规律一致，除壁面附近，数值也基本吻合。壁面附近的横向流速偏差主要由于横向流速相较于纵向流速数值小，致使相对误差值增大；壁面附近，水流波动大，测量精度受到影响。基于以上分析，该模型可用于模拟急弯河道的水流结构，为后续壁面切应力的准确计算提供了保证。

将2.1节经验公式与数值模拟值计算得到的急弯河道壁面切应力结果进行对比，如图 9所示。

图9(Fig. 9)

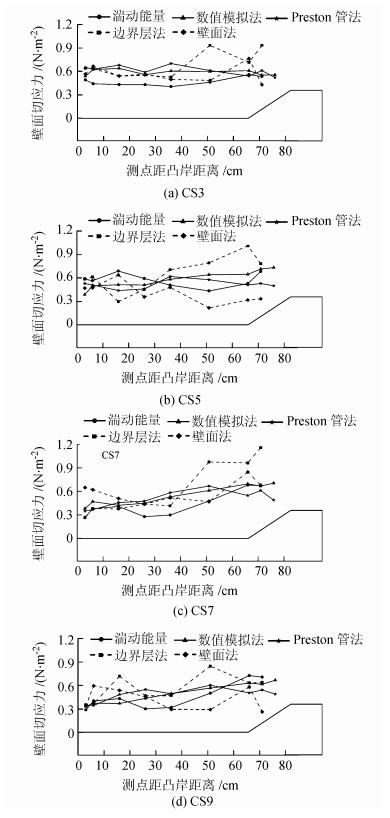图9 河床及岸坡壁面切应力计算结果对比图 Fig. 9 Calculation of boundary shear stress between different empirical methods

从图 9可以看出：壁面切应力沿底壁分布较均匀，而在坡脚附近波动剧烈。这是由于宽深比越大，底壁切应力分布越均匀^[1]，而坡脚附近受岸坡影响，水流条件复杂，3维性强，环流作用大。以上5种计算方法中，边界层参数法的计算值在断面横向分布上波动最为剧烈，壁面法次之，且这两种计算方法的壁面切应力分布规律也与其他3种方法不同。边界层参数法计算结果偏差是由于计算仅考虑了流体的纵向流速在单条测线上的非均匀分布，而忽略了流体的横向流动及脉动特性，在岸坡附近，环流作用及脉动强，相应的计算值偏离越明显。这表明边界层参数法应用于急弯水流时，常系数C无法适用，还有待进一步研究确定。此外，受ADV流速仪测量范围的限制，无法获取全水深的流速分布。壁面法是在对数律的基础上采用壁面附近的流速梯度计算壁面切应力，而在坡脚附近，流速的对数拟合度R²=0.5~0.75，这是由于该水槽虽为宽浅式，但水流宽深比相对较小，同时受弯道弯曲作用影响，各垂线最大流速位于自由面以下，此时的流速分布已偏离或部分偏离对数律^[18]，壁面法无法适用。此外，测点高度的准确性对计算结果影响也较大。相比之下，Preston管法、湍动能法以及数值模拟法的计算结果不仅在分布规律上，而且在数值大小上都吻合较好，具有一定的可靠性。另外，Preston管法和湍动能法在实际应用中简单易行，只需分别获取单点的流速和压强，测量工作量小，计算方法简单。因此，本文推荐使用Preston管法、湍动能法以及数值模拟法用于急弯河道壁面切应力的计算。

水槽内控制断面水深H=0.14 m保持不变，过水流量分别取50和30 L/s时，数值模拟得到的壁面切应力如图 10所示。

图10(Fig. 10)

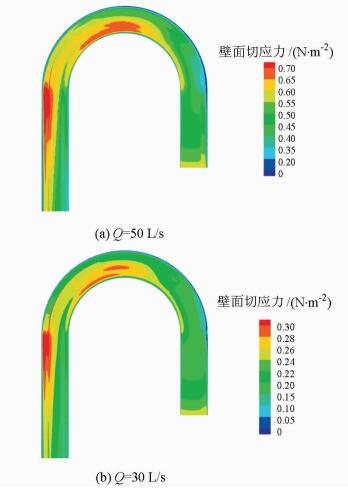图10 急弯河道河床及岸坡壁面切应力分布 Fig. 10 Distribution of boundary shear stress in bed and bank slope

从图 10可以看出：壁面切应力在进口顺直段内分布均匀，其值相对较小。进入弯道后，壁面切应力逐渐增大，分布也更不均匀。在弯道作用下，横断面最大壁面切应力位置发生偏移，在弯道中部，凸岸附近的壁面切应力较大，随着弯道内水流的不断调整，最大壁面切应力点逐渐偏移至凹岸，与主流的变化规律基本一致，这也说明水流流态及流速分布对壁面切应力有直接影响。水流进入出口顺直段后，岸坡附近的壁面切应力值达到最大，易于被冲刷。而后水流在下游顺直段内不断调整，流速分布趋于均匀，壁面切应力也相应降低。

当急弯河道出口水深保持不变，过水流量变化时，壁面切应力的总体变化规律基本相似，最大壁面切应力均位于弯道内110°断面的凸岸附近以及弯道出口下游0.5m断面的凹岸附近。壁面切应力随主流偏移过程中还体现出“大水趋直，小水坐弯”的特点。

对180°急弯河道内河床及岸坡的壁面切应力进行研究，得到以下成果：

1) Preston管法、湍动能法以及数值模拟法在急弯河道壁面切应力计算中吻合较好，计算结果具有一定的可靠性。

2) 在弯道作用下，弯曲水流最大壁面切应力位置在横向上发生偏移，从凸岸逐渐偏移至凹岸，与主流的变化规律基本一致。壁面切应力在岸坡附近，水流条件复杂，变化较为剧烈。

3) 急弯河道内最大壁面切应力位于弯道出口下游0.5 m断面的凹岸附近以及弯道内110°断面的凸岸附近。保持河道出口水深不变，仅过水流量变化时，河道内壁面切应力总体分布规律相似，并体现出“大水趋直，小水坐弯”的特点。