网络的开放性、互联性和共享性等特点使其遭受网络入侵的风险日益增加,攻击手段的智能化、复杂化和多样化对传统的防护方法提出了严峻的挑战[1]。在网络中,针对某一特定目标,仅实施攻击事件所包含的单一或部分攻击行为不一定能构成威胁,攻击者为提高攻击成功率,其攻击事件往往由多个独立攻击行为所组成。例如, 初期通过脆弱性扫描获得网络安全漏洞,实际上并不构成威胁,但如果通过掌握的安全漏洞展开进一步攻击,则其可能威胁网络安全。因此,分析网络面临的组合攻击形态,构建基于攻防行为的安全态势分析模型,对每一个独立及组合攻击行为进行威胁分析十分必要。
传统的攻击树模型[2-3]基于攻击行为进行建模,没有考虑防御因素影响。防御树模型[4-6]从防御的角度构建防御模型,但只能在叶节点添加防御措施,缺乏较好的可扩展性。故障树方法[7-8]通过分析目标事件发生的原因及彼此间的关系构建逻辑图,分析目标事件发生的原因和概率,但该方法适用于对系统内部产生的故障,难以对外部攻击进行分析。
针对以上问题,作者将攻击树和防御树进行整合进而构建网络攻防行为树,利用攻防树的特性描述具体的攻防行为场景,给出网络攻防树威胁算法,寻找可能存在的各种攻击行为组合,分析网络安全态势,对于发现网络关键脆弱性或链路, 有效配置网络资源, 优化网络系统等,具有重要理论意义。
1 网络攻防行为树模型网络安全态势可从目标攻击成功率和攻击成功后对网络系统损害效果两个角度分析。不同攻防行为相关概率差异给网络安全造成了不同影响,本文从攻防行为及检测概率的角度对网络安全态势进行分析。首先, 给出基于网络攻防行为树的安全态势分析架构,如图 1所示。
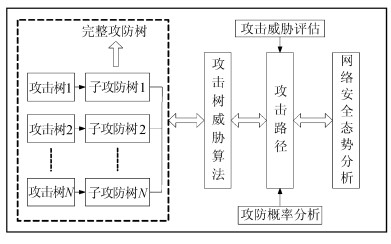 |
| 图1 基于攻防行为树的网络安全分析架构 Fig. 1 Architecture for the network security analysis based on attack-defense tree |
将攻防行为树定义为一个三元组ADT={N, E, ψ},其中:
1) 节点集为:
N={∀k, nk:nk=n0‖nk∈Aa‖nk∈Ad‖nk∈D}。
其中, n0表示根节点,代表攻击目标;D表示入侵检测节点,代表入侵检测设备;Aa和Ad分别表示攻击节点和防御节点,代表攻防双方可能采取的攻防行为。攻防行为树中的节点按照攻防性质可分为根结点 (目标节点)、入侵检测节点、攻击节点以及防御节点3类。按照层次结构,可以分为根结点、中间节点和叶节点:最上层的根结点即为攻击目标 (目标节点),要达到攻击目标的原子攻击行为和防御行为用叶节点表示,中间节点表示攻击的子目标。
2) 边集为:
E={∀k, ek:ek∈(ni, ψj)‖ek∈(ψi, ψj)}。
ADT的边存在两种情况:一种表示节点和逻辑门间的连接关系ek∈(ni, ψj);一种表示两逻辑门间的连接关系ek∈(ψi, ψj)。
3) 逻辑门集为:
ψ={∀nk∈N, ψ(nk):ψ(nk)∈{AND, OR}}。
其中,ψ(nk) 反映了节点nk与其子节点之间的逻辑关系。AND逻辑门表示目标节点的所有子节点所对应的子目标均满足时才能达到该目标;OR逻辑门表示满足任意节点即可。
攻防树模型利用树状结构描述网络可能遭受的攻击,一个简单的树形结构如图 2所示。
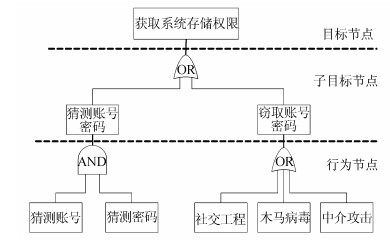 |
| 图2 攻击树范例 Fig. 2 Basic attack-defense action tree |
其中,最上层的根结点 (获取系统存储权限) 为目标节点,叶节点表示要获取系统存储权限所使用的方法。中间节点表示攻击子目标,按照逻辑关系而定,例如,窃取账号密码子目标的逻辑门为OR,因此,只要社交工程、木马病毒或中介攻击任意一个原子攻击行为完成即可;猜测账号密码子目标的逻辑门为AND,猜账号和猜密码两个原子攻击行为必须同时满足才能获得系统存储权限,任缺其一则无法达到目标,可见独立或部分的攻击行为并不一定构成威胁。
2 目标攻击成功率算法 2.1 目标攻击成功率目标攻击成功率从攻击与防御的角度出发,考虑存在的防御措施,从可被检测及防御两个方面来分析攻击事件的成功率,pgoal=f(attack, defense, prodection)。目标攻击成功率可以分为两部分;一是,攻击行为未被检测发现;二是,攻击行为被检测设备检测到但是未被防御措施成功阻止。网络攻防行为树的基本图形如图 3所示,即只存在一种攻击行为、一种防御行为和一个检测设备。攻击者发起攻击行为Aa的概率为pAa,防御者通过入侵检测D获知攻击信息并采用防御措施Ad,则攻击目标成功率pgoal=pAa(1-pDa+pDa(1-pda)),其中Pgoal表示攻击目标成功率,pDa为检测设备D成功检测到攻击行为Aa的概率,pda为防御措施Ad针对攻击行为Aa的防御有效率。
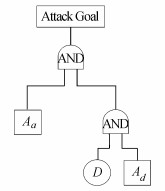 |
| 图3 基本攻防行为树 Fig. 3 Basic attack-defense action tree |
在基本攻防行为树的基础上从网络攻防行为、网络检测设备以及网络防御措施3方面对其进行扩展,如图 4所示。
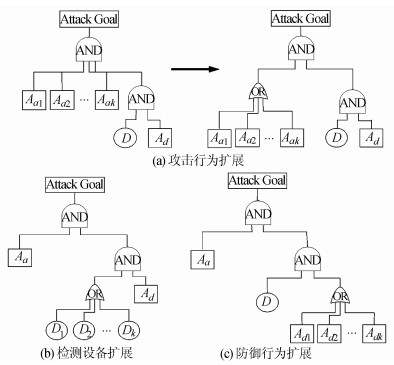 |
| 图4 基本攻防行为树扩展 Fig. 4 Extend of basic attack-defense action tree |
1) 攻击行为扩展。攻击者发起攻击行为Aa1, Aa2, …, Aak,攻击行为发生率为pAa1, pAa2, …, pAak,检测设备D对Aa1, Aa2, …, Aak的检测率分别为pD1, pD2, …, pDk,防御措施Ad针对攻击行为Aa1, Aa2, …, Aak的防御有效率分别为pda1, pda2, …, pdak,在此情形下,要求所有攻击行为均完成才能实现攻击目标。攻击行为Aai的攻击成功率为paisuc=pAai(1-pDi+pDi(1-pdai)),总目标攻击成功率:
| $ {p_{\rm{goal}}} = \prod\nolimits_{i = 1}^k {p_{ai}^{\rm{suc}}} = \prod\nolimits_{i = 1}^k {{p_{{A_{ai}}}}} (1-p_D^i + p_D^i(1-p_d^{ai})). $ |
如果逻辑节点为OR,则只要有一种攻击完成即可实现攻击目标。因此,则目标攻击成功率:
| $ {p_{\rm{goal}}} = \mathop {{\rm{max}}}\limits_{1 \le i \le k} {\rm{ }}p_{ai}^{\rm{suc}} = \mathop {{\rm{max}}}\limits_{1 \le i \le k} {\rm{ }}{p_{{A_{ai}}}}(1-p_D^i + p_D^i(1-p_d^{ai}))。$ |
2) 检测设备扩展。攻击者发起攻击行为Aa,网络中配置了检测设备D1, D2, …, Dk,检测设备对攻击行为的检测率分别为pD1a, pD2a, …, pDka,防御措施Ad针对攻击行为Aa的防御有效率为pda,则攻击行为未被检测到的概率
| $ \begin{array}{l} {p_{\rm{goal}}} = {p_{{A_a}}} \times (\prod\limits_{i = 1}^k {(1-p_{{D_i}}^a)} + \\ \;\;\;\;\;\;\;(1-\prod\limits_{i = 1}^k {(1-p_{{D_i}}^a)} )(1 - p_d^a)) = \\ \;\;\;\;\;\;\;{\rm{ }}{p_{{A_a}}} \times (1 - (1 - \prod\limits_{i = 1}^k {(1 - p_{{D_i}}^a)} ) \times p_d^a)。\end{array} $ |
3) 防御措施扩展。攻击者发起攻击行为Aa,检测设备D成功检测到攻击行为Aa的概率为pDa,防御措施为Ad1,Ad2,…, Adk,防御措施对攻击Aa的防御有效率分别为pd1a, pd2a, …, pdka,攻击行为未被检测到的概率为pAa(1-pDa),攻击行为被检测到但未有效实施防御概率为
| $ \begin{array}{l} {p_{\rm{goal}}} = {p_{{A_a}}}((1-p_D^a) + p_D^a\prod\limits_{i = 1}^k {(1-p_{di}^a))} = \\ \;\;\;{\rm{ }}{p_{{A_a}}}(1-p_D^a \times (1 - \prod\limits_{i = 1}^k {(1 - p_{di}^a))} )。\end{array} $ |
对图 4(b)和(c)进行整合,即同时对网络检测设备和防御措施进行扩展,如图 5所示。
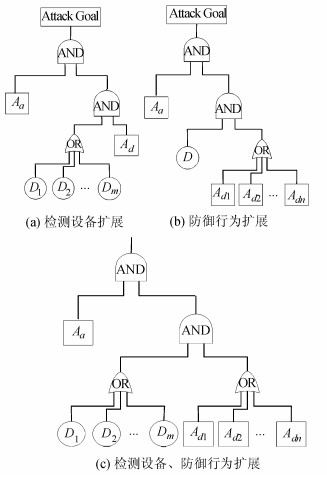 |
| 图5 攻防行为树扩展 Fig. 5 Extend of attack-defense action tree |
攻击者发起攻击行为Aa,检测设备D1, D2, …, Dm成功检测到攻击行为Aa的概率为pD1a, pD2a, …, pDma,防御措施为Ad1,Ad2,…, Adn,防御措施对攻击Aa的防御有效率分别为pd1a, pd2a, …, pdna,攻击行为未被检测到的概率为
| $ \begin{array}{l} {p_{\rm{goal}}} = {p_{{A_a}}}(1-(1-\prod\limits_{i = 1}^m {(1-p_{Dj}^a)} \times {\rm{ }}\\ \;\;\;\;\;\;\;\;\;\;(1 - \prod\limits_{j = 1}^n {(1 - p_{di}^a)} )))。\end{array} $ |
对于特定攻击目标常存在多条攻击路径,而不同的攻击路径达到目标的概率不同。通常情况下,理性攻击者会选择成功率最大的攻击路径,本文将攻击路径的最大成功率作为攻击目标成功率,即:
Pgoal=max (P(PATHS1), P(PATHS2), …,P(PATHSn))
给出如下攻击目标攻击成功率算法:
Algorithm: Computer_Attack_PATH (Tr) and Pgoal
Input:An attack-defense tree T with r being the root,
Pgoal=0
Output:attack-strategy,Pgoal
1. If r is the only node of the tree T then
2. return path (r)=1
3. else
4. let v1, v2, …, vk be the k children nodes of r
5. for i=1 to k do
6. Computer_Attack_PATHs (Tvi) and Pgoal
7. end for i
8. do case
9. case 1:r is OR node
10.
11. case 2:r is AND node
12.
13. end case
14. end If
3 网络安全态势分析依据风险定义,攻击事件的风险值Rgoal等于攻击事件的成功概率Pgoal乘以其对目标造成的损害Ugoal,即R(Aa)goal=UgoalAa×PgoalAa。网络系统根据其用途及防护目标不同,相应的安全属性指标也不相同。攻击行为对网络安全性造成的影响可以用网络系统安全度量指标的下降程度来描述,本文主要考虑机密性、完整性和可用性3个网络系统安全属性指标,应用多属性效用理论来度量目标节点的安全量化值:Ugoal=λCU(C)+λIU(I)+λAU(A),其中:Ugoal为攻击目标达成对网络系统造成的损害,λC、λI、λA表示各安全指标的权重,反映各安全属性对网络影响程度,U(C)、U(I)、U(A) 为各安全指标的效用性。
对于特定的攻击目标,最大的目标攻击成功概率与攻击对目标造成损害的乘积即是该目标的风险值,用Rgoal表示:RgoalwithoutAd=Ugoal×max PgoalwithoutAd,RgoalwithAd=Ugoal×max PgoalwithAd。RgoalwithoutAd、RgoalwithAd分别为系统不采取防御措施和采取防御措施时的网络风险值,PgoalwithoutAd、PgoalwithAd分别为未采取防御策略和采取防御措施时攻击目标达成概率。防御措施的防御效果EAd可用损害的差值表示,亦可反映网络的安全性:
| $ \begin{array}{l} {E_{{A_d}}} = \Delta Ris{k_{{\rm{goal}}}} = Risk_{{\rm{goal}}}^{{\rm{without}}{A_d}}-Risk_{{\rm{goal}}}^{{\rm{with}}{A_d}} = \\ \;\;\;\;\;\;\;\;\;{U_{{\rm{goal}}}} \times {\rm{max}}P_{{\rm{without}}{A_d}}^{{\rm{goal}}}-{U_{{\rm{goal}}}} \times {\rm{max}}P_{{\rm{with}}{A_d}}^{{\rm{goal}}}。\end{array} $ |
为验证网络攻防行为树模型的可行性和有效性,在文献[9]中BGP (border gateway protocol) 攻击树的基础上构建攻防行为树模型,如图 6所示。攻防行为信息如表 1和2所示, 检测信息如表 3所示,对抗信息如表 4所示。
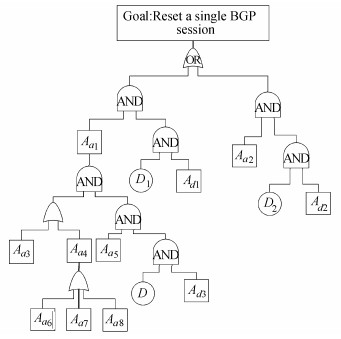 |
| 图6 BGP攻防行为树 Fig. 6 Attack-defense tree of BGP |
| 表1 攻击行为信息 Tab. 1 Information of network attack action |
 |
| 表2 防御行为信息 Tab. 2 Information of network defense action |
 |
| 表3 检测信息 Tab. 3 Information of network detection |
 |
| 表4 攻防对抗信息 Tab. 4 Information of attack-defense action |
 |
为达成目标Reset a single BGP session,攻击者存在5条攻击路径可供选择,由攻击目标攻击成功率算法可计算每条攻击路径的成功概率:
| $ \begin{array}{*{35}{l}} PATH1:{{A}_{a2}}({{D}_{2}},{{A}_{d2}})\to Goal; \\ \ \ \ \ \ \ \ \ \ \ \ P_{\text{goal}}^{\text{with}{{A}_{d}}}\left( PATH1 \right)=0.26。\\ PATH2:{{A}_{a3}}\times {{A}_{a5}}({{D}_{3}},{{A}_{d3}})\to {{A}_{a1}}({{D}_{1}},{{A}_{d1}})\to Goal; \\ \ \ \ \ \ \ \ \ \ \ \ P_{\text{goal}}^{\text{with}{{A}_{d}}}\left( PATH2 \right)=0.09。\\ PATH3:{{A}_{a6}}\to {{A}_{a4}}\times {{A}_{a5}}({{D}_{3}},{{A}_{d3}})\to {{A}_{a1}}({{D}_{1}},{{A}_{d1}})\to Goal; \\ \ \ \ \ \ \ \ \ \ \ \ P_{\text{goal}}^{\text{with}{{A}_{d}}}\left( PATH3 \right)=0.03。\\ PATH4:{{A}_{a7}}\to {{A}_{a4}}\times {{A}_{a5}}({{D}_{3}},{{A}_{d3}})\to {{A}_{a1}}({{D}_{1}},{{A}_{d1}})\to Goal; \\ \ \ \ \ \ \ \ \ \ \ \ P_{\text{goal}}^{\text{with}{{A}_{d}}}\left( PATH4 \right)=0.04。\\ PATH5:{{A}_{a8}}\to {{A}_{a4}}\times {{A}_{a5}}({{D}_{3}},{{A}_{d3}})\to {{A}_{a1}}({{D}_{1}},{{A}_{d1}})\to Goal; \\ \ \ \ \ \ \ \ \ \ \ \ \ P_{\text{goal}}^{\text{with}{{A}_{d}}}\left( PATH5 \right)=0.06。\\ \end{array} $ |
由此可见,攻击路径PATH1概率最大,因为其攻击手段最为直接,且面临的检测和防御措施较少。当系统没有布置防御措施时,通过目标攻击成功率算法计算上述5条攻击路径的成功概率如下:
| $ \begin{array}{*{35}{l}} PATH1:{{A}_{a2}}({{D}_{2}})\to Goal, \\ \ \ \ \ \ \ \ \ \ \ \ \ \ P_{\text{goal}}^{\text{without}{{A}_{d}}}\left( PATH1 \right)=0.4。\\ PATH2:{{A}_{a3}}\times {{A}_{a5}}({{D}_{3}})\to {{A}_{a1}}({{D}_{1}})\to Goal, \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ P_{\text{goal}}^{\text{without}{{A}_{d}}}\left( PATH2 \right)=0.21。\\ PATH3:{{A}_{a6}}\to {{A}_{a4}}\times {{A}_{a5}}({{D}_{3}})\to {{A}_{a1}}({{D}_{1}})\to Goal, \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ P_{\text{goal}}^{\text{without}{{A}_{d}}}\left( PATH3 \right)=0.07。\\ PATH4:{{A}_{a7}}\to {{A}_{a4}}\times {{A}_{a5}}({{D}_{3}})\to {{A}_{a1}}({{D}_{1}})\to Goal, \\ \ \ \ \ \ \ \ \ \ \ \ \ \ P_{\text{goal}}^{\text{without}{{A}_{d}}}\left( PATH4 \right)=0.105。\\ PATH5:{{A}_{a8}}\to {{A}_{a4}}\times {{A}_{a5}}({{D}_{3}})\to {{A}_{a1}}({{D}_{1}})\to Goal, \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ P_{\text{goal}}^{\text{without}{{A}_{d}}}\left( PATH5 \right)=0.14。\\ \end{array} $ |
在没有防御措施的情况下,5条攻击路径的攻击成功率均得到增大,且PATH2至PATH5概率增大倍数显著高于PATH1,因为后4条路径采取的多攻击行为组合,在没有防御措施的情况下,其成功概率会高于单攻击行为的成功概率,与实际情况相符。
假设攻击目标的网络安全属性向量为 (200,150,300),其影响权重向量为 (0.35,0.25,0.4),各防御措施的防御效果:
| $ \begin{array}{l} \Delta Ris{k_{{\rm{goal}}}}\left( {PATH1} \right) = 31.85, \\ \Delta Ris{k_{{\rm{goal}}}}\left( {PATH2} \right) = 27.3, \\ \Delta Ris{k_{{\rm{goal}}}}\left( {PATH3} \right) = 9.1, \\ \Delta Ris{k_{{\rm{goal}}}}\left( {PATH4} \right) = 14.8, \\ \Delta Ris{k_{{\rm{goal}}}}\left( {PATH5} \right) = 18.2。\end{array} $ |
随着信息化的全面推进与网络的广泛应用,网络安全形势日益严峻,网络安全问题的研究成为热点。论文将原有攻击树模型进行扩展,构建了网络攻防行为树模型,利用博弈论和攻防树的特性描述具体的攻防事件场景,分析了不同层面攻击行为的逻辑关系,通过整合各种不同层次攻击事件对应的攻防树以获得完整网络攻防行为树,给出了的网络目标攻击成功率算法,从攻防行为概率的角度分析了网络安全态势。该方法能够在任意节点添加和删除攻防行为,具有较强的可扩展性,可为网络管理者与运营者提供科学的决策依据。
| [1] |
Chen Yongqiang, Fu Yu, Wu Xiaoping. Security analysis of complex network based on system brittleness map[J]. Journal of Naval University of Engineering, 2013, 25(3): 30-33. [陈永强, 付钰, 吴晓平. 基于系统脆性图的复杂网络安全性分析[J]. 海军工程大学学报, 2013, 25(3): 30-33.] |
| [2] |
Zhang Kailun, Jiang Quanyuan. Evaluating the weakness of WAMS communication system based on attack tree-model[J]. Protection and Control of Electronic System, 2013, 41(7): 116-122. [张凯伦, 江全元. 基于攻击树模型的WAMS通信系统脆弱性评估[J]. 电力系统保护与控制, 2013, 41(7): 116-122.] |
| [3] |
Niu Binru, Liu Peiyu, Duan Linshan. A improved attack tree-based trojan analysis and detection[J]. Computer Application and Software, 2014, 31(3): 277-280. [牛冰茹, 刘培玉, 段林珊. 一种改进的基于攻击树的木马分析与检测[J]. 计算机应用与软件, 2014, 31(3): 277-280.] |
| [4] |
Bistarelli S, Dall'Aglio M D, Peretti P. Strategic games on defense trees[M]. Heidelberg: Springer, 2007, 1-15.
|
| [5] |
Bistarelli S, Fioravanti F, Peretti P.Defence trees for economic evaluation of security Investments[C]//Proceedings of the First International Conference on Availabibty Reliability and Security, 2006(ARES'06).Vienna:IEEE, 2006:416-423.
|
| [6] |
Zhang Dehong. The research of attack-defense strategy and active defense in network security[J]. Natural Sciences Journal of Harbin Normal University, 2012, 28(2): 49-53. [张德洪. 网络安全中攻防策略与主动防御研究[J]. 哈尔滨师范大学 (自然科学学报), 2012, 28(2): 49-53.] |
| [7] |
Zhang Honglin, Zhang Chunyuan, Liu Dong, et al. A method of disjoint quantitative analysis for dynamic fault tree[J]. Journal of Computer Research and Development, 2012, 49(5): 983-995. [张红林, 张春元, 刘东, 等. 动态故障树的不交化定量分析方法[J]. 计算机研究与发展, 2012, 49(5): 983-995.] |
| [8] |
Xu Binfeng, Huang Zhiqiu, Hu Jun, et al. A method for quantitative analysis of state/event fault tree[J]. Acta Electronica sinica, 2013, 41(8): 1480-1486. [徐丙凤, 黄志球, 胡军, 等. 一种状态事件故障树的定量分析方法[J]. 电子学报, 2013, 41(8): 1480-1486.] |
| [9] |
Convery S, Cook D, Franz M.An attack tree for the border gateway protocol[R].Washington DC:IETF, 2004.
|
 2017, Vol. 49
2017, Vol. 49

