2. 南昌航空大学 软件学院, 江西 南昌 330063;
3. 南昌航空大学 信息工程学院, 江西 南昌 330063
2. School of Software, Nanchang Hangkong Univ., Nanchang 330063, China;
3. School of Info. Eng., Nanchang Hangkong Univ., Nanchang 330063, China
无线传感器网络 (wireless sensor networks,WSNs) 中,节点的绝大部分能量消耗于无线通信模块的数据传输[1]。若能预测链路质量,可为MAC协议、路由协议和拓扑控制提供参考,选择高质量的链路进行通信,不仅可以提高数据传输的可靠性,还能降低节点的能耗,延长网络寿命。因此,值得研究WSNs的链路质量预测方法。国内外学者在WSNs链路质量预测方法上进行了探索与实践,主要分为基于链路特性、基于概率估计以及基于智能学习的3类方法。基于智能学习的链路质量预测采用机器学习、模式匹配等方法进行建模,具有较高的准确率,是目前WSNs链路质量预测方法的主流。
文献[2]提出基于模式匹配的链路质量预测机制XCoPred,采用信噪比 (signal to noise ratio,SNR) 度量链路质量,在802.11室内网上验证了方法的有效性,但是单一链路指标不能全面反映链路质量;文献[3]采用监督式学习算法构建了链路质量预测模型,综合考虑接收信号强度指示 (received signal strength indicator,RSSI)、链路质量指示 (link quality indicator,LQI)、缓存区大小等因素,实验证明机器学习方法在链路质量预测上具有明显的优势,但是物理层参数对硬件依赖性较强,当RSSI值接近芯片接收阈值时,较易出现“长尾现象”,造成欠学习情况;文献[4]提出4C链路质量预测模型,将包接收率 (packet reception rate,PRR) 和物理层参数RSSI、LQI、SNR作为输入,采用Logisitc回归算法预测PRR;文献[5]提出综合性评估的链路质量分类预测机制,从可靠性、波动性和丢包突发性3方面,采用模糊规则定义模糊逻辑链路质量指标 (fuzzy-logic based link quality index,FLI),利用朴素贝叶斯网络建立预测模型,获得了较好预测准确率,但是划分的链路等级过少,无法灵敏反映链路状态变化;文献[6]提出基于模糊支持向量回归机的链路质量预测模型,采用混沌粒子群优化算法对模型参数进行优化,实验结果表明具有较好的预测性能。
贝叶斯网络[7](Bayesian networks, BN) 是一种采用有向无环图表达概率关系的理论,被广泛应用于不确定性和概率性事物的表达,凭借其强大的知识表达和推理能力,具有良好的分类性能,在处理不确定性问题方面具有独特的优势[8],成为人工智能学科中处理不确定问题方面的热门建模与分析工具之一。在贝叶斯网络基础上发展而来的动态贝叶斯网络[9](dynamic Bayesian networks,DBNs) 是贝叶斯理论在时间序列上的拓展,能实现动态时序数据的分析与预测。链路质量受环境噪声、信号干扰和多径效应等不确定因素的影响,链路质量预测的实质为链路质量的时序预测。本文从信道质量、链路稳定性和非对称性3方面对链路质量进行综合评价,提出基于动态贝叶斯网络的WSNs链路质量预测方法。
1 基于DBN的链路质量预测模型 1.1 链路质量参数的选取基于硬件的链路质量参数RSSI、LQI、SNR能够快速感知链路的变化,但不能很好体现链路的稳定性;基于软件的链路质量参数PRR能够较准确地反映链路的稳定性,但不能很好体现链路的灵敏性。文献[5, 10]通过PRR的奇异系数刻画链路质量的稳定性CV=σ(PRR)/μ(PRR),文献[10]通过上下行PRR值定义链路质量的非对称水平 (asymmetry level,ASL),即ASL=|PRRup-PRRdown|,但PRR的获取需要发送大量的探测包,因此采用PRR来计算ASL和CV将带来过多的能量消耗。
本文综合考虑链路质量参数的灵敏性和稳定性,分析RSSI、LQI、SNR及PRR的相关性,进而对链路质量参数进行选取。LQI与PRR具有较强的相关性[11],由LQI可以估计PRR值;通过RSSI间接得到SNR,因此RSSI与SNR间具有强相关性。本文改进稳定性CV和非对称水平ASL的定义,如式 (1)、(2) 所示:
| $ CV = \frac{{\sigma \left( {LQI} \right)}}{{\mu \left( {LQI} \right)}} $ | (1) |
| $ ASL = \left| {LQ{I_{{\rm{up}}}}-LQ{I_{{\rm{down}}}}} \right| $ | (2) |
选取SNR、CV、ASL为链路质量参数。
1.2 基于K-means聚类的参数离散化连续变量离散化是BN参数学习中面临的一个重要问题,它的好坏直接影响着贝叶斯网络中参数学习和推理的效果[12]。因此,在对BN模型的参数学习之前,需要将特征变量进行离散化处理,获得各链路质量参数的阈值区间,构建BN中各个特征变量的状态属性。K-means算法是聚类分析中使用较多的可靠方法之一,具有快速、简单的特点,适用于大规模数据集挖掘。本文选择K-means聚类算法对链路质量参数进行离散化处理。
K-means算法描述如下:
1) 从n个数据样本中,随机选择k个样本作为聚类的中心;
2) 计算各样本到聚类中心的距离,根据最小距离原则将样本划归到相应的聚类;
3) 根据聚类结果,采用平均值重新计算该k个聚类的中心;
4) 重复步骤2) 和步骤3),直到聚类结果不再变化。
K-means聚类算法的时间复杂度为O(nkt),其中,n为数据集样本个数,t为迭代运算次数,k为聚类数目。
1.3 链路质量等级的划分本文采用熵值法确定链路质量参数指标权重,借助贴近度分析法[13]在解决多属性决策问题上的优势,划分链路质量等级。
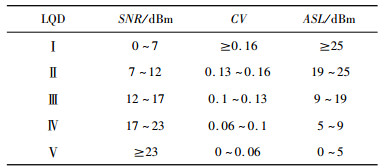
1.3.1 链路质量的等级综合SNR、CV和ASL这3个链路质量参数,采用链路质量等级描述链路质量状态,将链路质量划分成5个等级 (link quality degree,LQD),即等级Ⅰ~等级Ⅴ,其中,等级Ⅴ最佳,等级Ⅳ次之,等级Ⅰ最差。设V={vk|vk=k, k∈[1, 5]}为等级的判定集,链路质量等级及含义如表 1所示。
| 表1 链路质量等级及含义 Tab. 1 Link quality degrees and meaning |
 |
1.3.2 链路质量参数的权重
一般采用主成分分析法[14]、层次分析法[15]、或熵值法[16]确定参数的权重。本文采用熵值法计算链路质量参数的权重,根据各指标参数所含信息有序程度来确定权重,能够有效消除参数权重计算的主观因素干扰,使评价结果更加客观和贴近实际。
计算步骤如下:
1) 选择m个指标参数和n个样本对象,则xij为第i个样本对象的第j个指标参数值 (i=1, 2, …, n; j=1, 2, …, m)。
2) 根据式 (3) 进行归一化,将指标参数的绝对值转化为相对值x′ij。
| $ x_{ij}^{'}=\left\{ \begin{array}{*{35}{l}} \frac{{{x}_{ij}}-\text{min}\{{{x}_{ij}},L,{{x}_{nj}}\}}{\text{max}\{{{x}_{ij}},L,{{x}_{nj}}\}-\text{min}\{{{x}_{ij}},L,{{x}_{nj}}\}},正向指标; \\ \frac{\text{max}\{{{x}_{ij}},L,{{x}_{nj}}\}-{{x}_{ij}}}{\text{max}\{{{x}_{ij}},L,{{x}_{nj}}\}-\text{min}\{{{x}_{ij}},L,{{x}_{nj}}\}},负向指标 \\ \end{array} \right. $ | (3) |
3) 计算第j个指标参数的熵值ej为:
| $ {e_j} =-\frac{1}{{{\rm{ln}}m}}\sum\limits_{i = 1}^m {{p_{ij}}{\rm{ln}}({p_{ij}})}, \left( {i = 1, 2, \cdots, n;j = 1, 2, \cdots, m} \right) $ | (4) |
满足ej≥0,其中,pij为第j个指标参数下第i个样本对象的比重,如式 (5) 所示:
| $ {{p}_{ij}}=\frac{x_{ij}^{'}}{\sum\limits_{i=1}^{n}{x_{ij}^{'}}} $ | (5) |
4) 得到信息效用值dj,如式 (6) 所示:
| $ {d_j} = 1-{e_j} $ | (6) |
5) 计算指标权重向量W={w1, wj, …, wm},其中,wj如式 (7) 所示:
| $ {w_j} = \frac{{{d_j}}}{{\sum\limits_{j = 1}^m {{d_j}} }} $ | (7) |
贴近度描述2个模糊子集间的贴近程度,分为对称贴近度和非对称贴近度[13]。其中,非对称贴近度分析法能有效避免最大隶属原则的缺陷,在等级划分中更具有效性[17]。本文选用非对称贴近度评价链路质量,评价过程如下:
1) 确定样本的隶属度模糊矩阵R。
定义样本的特征向量L=[α1, αi,…, αm],其中,i=1, 2, …, m,m为链路质量参数个数。依据隶属度函数,计算各特征值αi对应的隶属度rij,得到隶属度模糊矩阵如式 (8) 所示:
| $ \boldsymbol{R} = \left[{\begin{array}{*{20}{c}} {{r_{11}}}&{{r_{12}}}& \cdots &{{r_{1t}}}\\ {{r_{21}}}&{{r_{22}}}& \cdots &{{r_{2t}}}\\ \cdots & \cdots &{}& \cdots \\ {{r_{m1}}}&{{r_{m2}}}& \cdots &{{r_{mt}}} \end{array}} \right] = {({r_{ij}})_{m \times t}}, \left( {i = 1, 2, \cdots, m;j = 1, 2, \cdots, t} \right) $ | (8) |
式中,rij为链路质量参数i的等级j隶属度值,t为代表各链路质量参数的等级级数,这里m=3,t=5。
2) 确定链路质量模糊评价子集C:
| $ \boldsymbol{C} = \boldsymbol{W} \times \boldsymbol{R} = {({c_j})_{1 \times t}} $ | (9) |
式中,W为链路质量参数权重向量,W=(ω1, ω2, …, ωm)。
3) 确定链路质量的评价等级。
① 非对称贴近度[17]
计算方法为:
| $ N\left( {\boldsymbol{A}, \boldsymbol{B}} \right) = 1-\frac{2}{{n\left( {n + 1} \right)}}\sum\limits_{k = 1}^n {\left| {{\mu _A}({v_k})-{\mu _B}({v_k})} \right|\cdot k} $ | (10) |
式中,μA(vk) 是A所对应的对象隶属于等级vk的隶属度。
② 对模糊子集C标准化
标准化的原则为:对任意给定的j∈Jn(Jn=[1, t]),按下标i和j的距离|i-j|,对C中的元素进行重新排序。将cj置于第1位,对任何的i1, i2∈Jn,若|i1-j| < |i2-j|,则排序中ci1在ci2前面;若|i1-j|=|i2-j|且i1 < i2,则ci1排在ci2前面。C标准化后的序列为cj, cj-1, cj+1, cj-2, cj+2, …,记为C(j),如式 (11) 所示:
| $ {C^{(j)}} = ({c_j}, {c_{j-1}}, {c_{j + 1}}, {c_{j-2}}, {c_{j + 2}}, \cdots ) $ | (11) |
相应地,目标模糊子集D的最理想情况是Dj=(0, …, 1, …, 0)(其中,1是第j个分量),对其标准化后得到D1=(1, …, 0, …, 0)。
③ 计算非对称贴近度N(C, D),确定链路质量等级。按式 (10) 计算标准化后的模糊子集C与D间的贴近度,如式 (12) 所示:
| $ N\left( {\boldsymbol{C}, \boldsymbol{D}} \right) = N({\boldsymbol{C}^{(j)}}, {\boldsymbol{D}_1}) = 1-\frac{1}{n}\sum\limits_{j = 1}^n {\left| {({c_j}-{d_j})} \right|\cdot j} $ | (12) |
则有N(C, D)=max{N(C(j), D1)},该样本对象的链路质量等级结果为vj=j, j∈[1, t],即为最大贴近度中C(j)所对应的j的值。
1.4 构建基于DBN的链路质量预测模型 1.4.1 DBN结构的确定DBN模型中包含观测节点和隐含节点。本文中,观测节点为所选链路质量参数,隐含节点为根据观测节点的状态推理得到的未知节点,即待预测的链路质量等级。基于DBN的链路质量预测模型的可定义为 (B0, B→),其中, B0表示初始的DBN模型结构,如图 1所示,B→为DBN转移网络,如图 2所示。
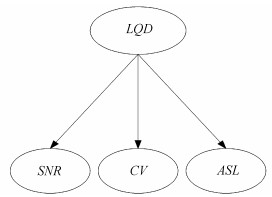 |
| 图1 DBN初始网络B0 Fig. 1 DBN initial network B0 |
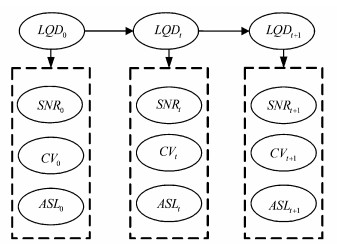 |
| 图2 DBN转移网络B→ Fig. 2 DBN transfer network B→ |
SNR、CV、ASL为观测变量,LQD为隐藏变量。
考虑到WSNs节点的存储及计算能力有限,如果时间片过大,不仅占据过多的存储空间,而且DBN转移网络在时间序列上的展开推理过程计算复杂度将直线增加;若时间片过小,链路质量的预测准确率又无法得到保障。本文设置DBN的时间片数量为3,通过前2个时间片的观测数据,预测第3个时间片的链路质量等级。
1.4.2 DBN模型的参数学习采用EM[18]算法进行DBN模型的参数学习,对初始化概率分布进行修正。EM算法通过期望的统计来替代实际的统计值P(x1:T|y1:T),是一个依次计算期望的统计值和模型参数λ的迭代过程,描述如下:
1) Expectation过程。初始化模型参数λ并迭代,第k次迭代过程如式 (13) 所示。
| $ \begin{array}{l} E[N\left( {i, j} \right)|{\lambda ^k}\left] { = E} \right[\sum\limits_{t = 2}^T {I({x_{t-1}} = i, {x_t} = j)} |{y_{1:T}}] = {\rm{ }}\\ \;\;\;\sum\limits_{t = 2}^T {P({x_{t -1}} = i, {x_t} = j|{y_{1:T}})} = \sum\limits_{t = 2}^T {{\xi _{t -1, t|T}}\left( {i, j} \right)} \end{array} $ | (13) |
式中,E[N(i, j)|λk]为期望足够统计值 (expectation sufficeient statistic,ESS)。
2) Maximization过程:目的是保证给定数据下,模型的log似然值最大,即
| $ Q(\lambda \left| {{\lambda ^k}} \right.) = {E_{x(1:T)}}[P({y_{1:T}}, {x_{1:T}})\left| {\lambda )} \right.{\lambda ^k}] $ | (14) |
根据当前链路质量测试数据,更新模型中观测节点的状态,利用节点间的概率传播网络推理计算出链路质量等级的状态分布。具体步骤如下:
1) 观测证据的更新。将链路探测得到的链路质量测试参数,对收集的数据进行离散化处理后得到各特征变量的当前状态,并对模型中对应的状态值进行更新。
2) 推理计算下一刻链路质量等级概率。根据最新的链路质量证据信息,在条件概率的作用下,触发网络推理,完成网络参数的信息更新。DBN推理过程实质为在给定贝叶斯网络结构上的概率计算。链路质量的时序预测问题,可表示为已知X1:t的观测值,预测t+1时刻的无线链路质量等级Ct+1,即:
| $ P({C_{t + 1}}|{X_{1:t}}) = \sum P({C_{t + 1}}|{X_{t + 1}})P({X_{t + 1}}|{X_{1:t}}) $ | (15) |
| $ P({c_i}|{X_{1:t}}) = {\rm{max}}\{ P({C_{t + 1}}|{X_{1:t}})\} $ | (16) |
选取概率最大值所对应的等级ci,即为下一时刻的链路质量等级。
2 实验设计与分析本文进行了多个场景下的实验。选用CrossBow公司的TelosB节点收集数据,在自主研发的无线传感器网络链路质量测试平台 (wireless sensor networks link quality testbed,WSNs-LQT) 上进行分析,实验过程中还用到仿真工具MatlabR2012a、分析工具SPSS、BN图形仿真工具GeNIe2.0、BN的Matlab工具箱FullBNT-1.0.7等。
2.1 实验场景选择校园树林,交通主干道和室内走廊3个场景进行链路质量测试实验,如图 3~5所示,在各实验场景下均部署了一个小型星形WSNs网络,包括10个感知节点和1个Sink节点。
 |
| 图3 校园树林 Fig. 3 Woods |
 |
| 图4 交通主干道 Fig. 4 Road |
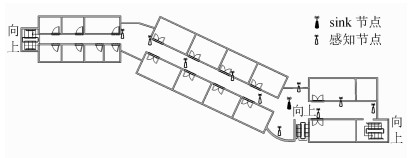 |
| 图5 室内走廊 Fig. 5 Indoor |
2.2 实验参数
实验参数如表 2所示。
| 表2 链路质量测试参数设置情况 Tab. 2 Link quality test parameter settings |
 |
2.3 实验分析 2.3.1 链路质量参数的相关性
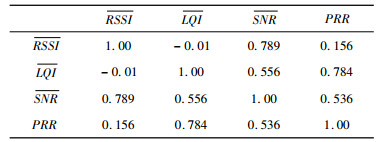
采用SPSS统计分析工具对采集的数据进行相关性分析,得到3个场景下的RSSI、LQI、SNR及PRR之间相关性,分别如表 3~5所示。
| 表3 校园树林场景下的相关性 Tab. 3 Correlation of parameters in woods scenario |
 |
| 表4 交通主干道场景下的相关性 Tab. 4 Correlation of parameters in road scenario |
 |
| 表5 室内走廊场景下的相关性 Tab. 5 Correlation of parameters in indoor scenario |
 |
校园树林场景中,由于树木等障碍物的遮挡,节点间多为非视距下的链路通信。与SNR相比,LQI与PRR具有较强相关性,RSSI与SNR相关性明显高于RSSI与LQI。
在交通主干道旁,车辆,行人较多,环境变化较为频繁,链路的干扰因素也存在多样化,实验中链路质量测试值波动较为明显。表 4可以看出,与PRR相关性最强的是LQI,其次是SNR。此时RSSI与SNR之间相关性较弱。
室内走廊场景中,主要有无线wifi信号,移动信号,人员走动等干扰因素对链路质量产生影响。在室内走廊内场景下,与RSSI和SNR相比,LQI与PRR,SNR均表现出较强的相关性。
综上所述,3种实验场景下,与PRR相关性最强的是LQI,其次是SNR,最弱的是RSSI。SNR具有环境敏感性,此结果与文献[19]结论一致,而LQI值能够很好的反映链路质量的状态。另外,RSSI、LQI、SNR三者之间,SNR与RSSI的相关性较强。因此,本文在稳定性参数CV及非对称水平参数ASL的定义中,可用LQI替代PRR值,从而避免发送大量探测包带来的能量开销。
2.3.2 链路质量等级划分的验证本文从链路质量的信号质量,稳定性和非对称性等多维度对链路质量进行综合性评价,构建了综合性链路质量等级。
采用K-means对样本数据的各个参数进行离散化处理,得到各参数的离散区间如表 6所示。
| 表6 链路质量参数的离散区间 Tab. 6 Discrete interval of link quality parameters |
 |
在获得链路质量参数间的区间后,本文采用熵值法确定各参数的权值,并通过贴近度分析法计算确定链路质量样本的等级LQD。PRR值是链路质量参数中一个较为稳定的链路质量参数,是链路质量好坏的一个宏观体现,而LQD综合了链路信号质量,波动性及非对称性等特征,从多维度对链路质量进行描述。为了验证链路质量等级划分的有效性,本文链路质量参数SNR、CV、ASL及链路质量等级LQD与PRR进行对比分析。
图 6为校园树林场景下6号节点与Sink之间的100组链路样本等级时序图。从图 6中可以看出,SNR变化较为平缓,波动范围在15~25 dBm之间,属于Ⅲ~Ⅴ等级;稳定性参数CV变化较为剧烈在0~0.12波动,分别在Ⅲ~Ⅴ等级的范围内波动;非对称性参数ASL较为良好,波动范围Ⅳ~Ⅴ。此时链路的PRR在50%~95%之间波动,尤其在第10~第20个时间序列时,PRR波动较为明显。将链路质量等级Ⅰ~等级Ⅴ记作:vi∈[1, 5],归一化后,链路质量等级LQD的时序图如图 7所示。
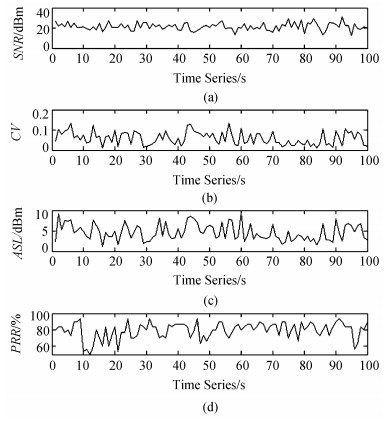 |
| 图6 SNR、CV、ASL及PRR的时序图 Fig. 6 Time series of SNR, CV, ASL and PRR |
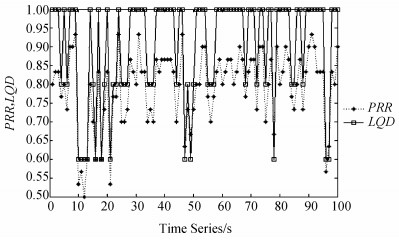 |
| 图7 链路质量等级时序图 Fig. 7 Time series of link quality degree |
从图 7中可以看出,开始时刻链路质量等级为Ⅴ,链路情况较好,当第10~第20个时间序列时,PRR波动较大,链路的稳定性出现下滑,链路质量等级相应在等级Ⅴ及等级Ⅲ间波动,而当第60~第80个时间序列时,PRR在0.85左右的小范围内波动,链路质量等级维持在等级Ⅴ,链路质量比较好。综上所述,综合性链路质量等级从信号质量,稳定性和非对称性等多维度对链路质量进行描述,能较好地反映链路质量的变化。
2.3.3 DBN预测模型的验证与对比为验证基于DBN链路质量预测模型的预测推理能力,本文选取某条链路的一段时间内的时间序列测试样本,将时间序列上前2个时间片上的链路质量参数SNR、CV、ASL作为观测数据输入,第3个时间片上的链路质量等级为输出,验证模型预测推理的合理性。
由于DBN模型推理计算过程是对上一时刻学习经验和知识的保存和积累,因此随着时间的展开,收集到的链路质量证据和确定性信息越来越多,推理预测的结果精确性不断提高,能有效克服了链路质量推理的不确定性。
推理过程中,根据预测推理所得的后验概率P(Ct+1|X1:t),确定下一时间片上的链路质量等级。图 8为各等级的概率。根据各等级的概率最大值,可以得到预测结果如图 9所示。
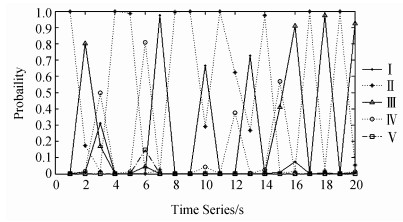 |
| 图8 DBN模型预测的等级概率 Fig. 8 Level probability predicted by DBN model |
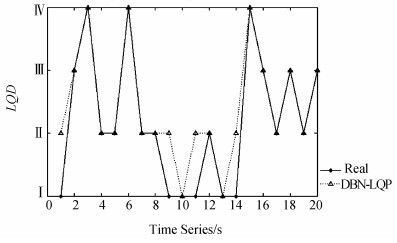 |
| 图9 DBN模型预测的结果 Fig. 9 Prediction result of DBN model |
为了进一步验证DBN预测模型的预测性能,本文选用4C[4]、FLI[5]模型分别在校园树林、交通主干道和室内走廊实验场景下进行对比分析,采用均方误差 (mean squared error, MSE) 来衡量预测模型准确率,从准确率、预测目标和等级3个方面进行对比,如表 7所示。其中,Target为预测目标。
| 表7 准确率、预测目标及等级对比 Tab. 7 Comparison of accuracy, target and level |
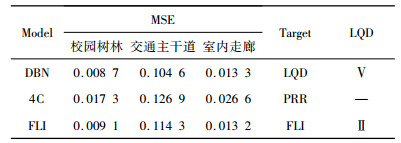 |
从表 7可以看出,本文提出的DBN链路质量预测模型及FLI模型,均采用链路质量等级作为预测目标,从链路质量参数的多维度对链路质量进行评价,与FLI仅将链路质量划分为2个等级相比,DBN模型能更为精细灵敏的反应链路质量状态。以上3个实验场景下,DBN链路质量预测模型均具有较高的准确率,其中在校园树林和室内走廊场景下,DBN与FLI链路质量预测模型准确率上区分并不显著,而在交通主干道应用场景下,环境的变化频繁,DBN链路质量预测模型仍然保持较高的准确率,比4C和FLI模型具有更好的稳定性,能够较好反映下一刻链路的变化趋势。
3 结论本文在分析现有链路质量预测方法的基础上,从链路信号质量,稳定性及非对称性等多维度对链路质量进行评价,采用贴近度分析法对链路质量等级进行了划分,能够较为全面地反应链路质量的状态,弥补了单一链路质量参数评价的不足。基于DBN理论构建了一种新的链路质量的时间序列预测方法,通过多场景下的训练和测试,实验验证了DBN链路质量预测模型的合理性。与4C和FLI预测模型相比,本文提出的DBN链路质量预测模型获得了更好的预测准确率且具有较好的环境适用性。
下一步拟从优化参数学习性能上提升模型预测的准确率,同时引入在线学习策略,进一步增强模型的环境适用性。
| [1] |
Yang Kai, Yang Xiaoyuan, Ma Jianfeng. A novel detection scheme based on D-S evidence theory in wireless sensor networks[J]. Journal of Sichuan University (Engineering Science Edition), 2016, 48(2): 118-124. [杨凯, 杨晓元, 马建峰. 无线传感器网络中一种基于D-S证据理论的监测机制[J]. 四川大学学报 (工程科学版), 2016, 48(2): 118-124.] |
| [2] |
Farkas K, Hossmann T, Legendre F, et al. Link quality prediction in mesh networks[J]. Computer Communications, 2008, 31(8): 1497-1512. DOI:10.1016/j.comcom.2008.01.047 |
| [3] |
Wang Yong, Martonosi M, Peh L S. Predicting link quality using supervised learning in wireless sensor networks[J]. ACM SIGMOBILE Mobile Computing and Communications Review, 2007, 11(3): 71-83. DOI:10.1145/1317425 |
| [4] |
Liu Tao, Cerpa A E.Foresee (4C):Wireless link prediction using link features[C]//Proceeding of the 10th International Conference on Information Processing in Sensor Networks (IPSN).Chicago:IEEE, 2011:294-305.
|
| [5] |
Guo Zhiqiang, Wang Qin, Wan Yadong, et al. A classification prediction mechanism based on comprehensive asessment for wireless link quality[J]. Journal of Computer Research and Development, 2013, 50(6): 1227-1238. [郭志强, 王沁, 万亚东, 等. 基于综合性评估的无线链路质量分类预测机制[J]. 计算机研究与发展, 2013, 50(6): 1227-1238.] |
| [6] |
Shu Jian, Tang Jin, Liu Linlan, et al. Fuzzy support vector regression-based link quality prediction model for wireless sensor networks[J]. Journal of Computer Research and Development, 2015, 52(8): 1842-1851. [舒坚, 汤津, 刘琳岚, 等. 基于模糊支持向量回归机的WSNs链路质量预测[J]. 计算机研究与发展, 2015, 52(8): 1842-1851.] |
| [7] |
Darwiche A. Bayesian networks[J]. Communications of the ACM, 2010, 53(12): 80-90. DOI:10.1145/1859204 |
| [8] |
Wu Qiwu, Liu Qingzi. Trusted model of secure routing for VANET based on Bayesian theory[J]. Journal of Sichuan University (Engineering Science Edition), 2015, 47(2): 129-135. [吴启武, 刘青子. 基于贝叶斯理论的VANET安全路由信任模型[J]. 四川大学学报 (工程科学版), 2015, 47(2): 129-135.] |
| [9] |
Murphy Kevin P. Dynamic bayesian networks[J]. Probabilistic Graphical Models, 2002, 42(2): 27-56. |
| [10] |
Baccour N, Koubâa A, Youssef H, et al.F-LQE:A fuzzy link quality estimator for wireless sensor networks[C]//Proceeding of the 7th European Conference on Wireless Sensor Networks (EWSN).Coimbra:Springer, 2010:240-255.
|
| [11] |
Baccour N, Puccinelli D, Voigt T, et al. Overview of link quality estimation[M]. Berlin: Springer, 2013, 65-86.
|
| [12] |
Zhou Xuan, Wang Lei, Zhu Yanguang, et al. A discretization method of continuous variable in Bayesian network parameter learning[J]. Couputer Simulation, 2009, 26(9): 136-139. [周旋, 王磊, 朱延广, 等. 贝叶斯网参数学习中连续变量离散化方法研究[J]. 计算机仿真, 2009, 26(9): 136-139.] |
| [13] |
Zhao Zhimiao, Sun Lina, Chen Su, et al. Application of the approaching degree method in riparian zone health assessment in Tieling section of Liao River[J]. Chinese Journal of Ecology, 2014, 33(3): 735-740. [赵志淼, 孙丽娜, 陈苏, 等. 贴近度分析法在辽河干流铁岭段河岸带健康评价中的应用[J]. 生态学杂志, 2014, 33(3): 735-740.] |
| [14] |
Jianhua Jin.The 3G network comprehensive performance evaluation based on PCA method[D].Dalian:Dalian Unversity of technology, 2013. 金建华. 基于主成分分析法的3G网络综合性能评价[D]. 大连: 大连理工大学, 2013. |
| [15] |
Guo Jinyu, Zhang Zhongbin, Sun Qingyun. Study and applications of analytic hierarchy process[J]. China Safety Science Journal, 2008, 18(5): 148-153. [郭金玉, 张忠彬, 孙庆云. 层次分析法的研究与应用[J]. 中国安全科学学报, 2008, 18(5): 148-153.] |
| [16] |
Zhu Fangxia, Chen Huayou. A method of entropy for obtaining the attribute weights of interval numbers decision-making matrix[J]. Journal of Anhui University (Natural Science Edition), 2006, 30(5): 4-6. [朱方霞, 陈华友. 确定区间数决策矩阵属性权重的方法——熵值法[J]. 安徽大学学报 (自然科学版), 2006, 30(5): 4-6.] |
| [17] |
Hua Zhongsheng, Liang Liang. Multi-objective classification algorithm based on fuzzy closeness degree[J]. Operations Research and Management Science, 1994, 3/4(supp1): 19-24. [华中生, 梁梁. 基于模糊贴近度的多目标分类算法[J]. 运筹与管理, 1994, 3/4(增刊1): 19-24.] |
| [18] |
Mclachlan G J, Krishnan T. The EM algorithm and extensions[J]. Biometrics, 1998, 382(1): 154-156. |
| [19] |
Son D, Krishnamachari B, Heidemann J.Experimental analysis of concurrent packet transmissions in wireless sensor networks[C]//Proceeding of the 4th ACM SenSys Conference.Colorado:ACM, 2006:237-249.
|
 2017, Vol. 49
2017, Vol. 49


