可计算RFID (computational radio frequency identification,CRFID) 是一种捕获射频能量[1]工作的无源传感节点。它们沿袭了RFID的后向散射通信模式,即从阅读器发出的射频信号中获取能量,将编码数据调制在接收的信号中反射回阅读器。典型的CRFID系统有Intel和华盛顿大学联合开发的WISP (Wireless Identification and Sensing Platform)[2]和密歇根大学在WISP基础上开发的UMASS Moo[3]等。本文考虑的场景是CRFID用于移动感知,当运动到阅读器附近时,将缓存的数据通过后向散射通信传输给阅读器。CRFID在移动过程中其能量捕获条件和信道质量都处于动态变化中。当能量捕获条件较差时,CRFID需要经历较长的充电时间才能达到工作电压;当信道质量较差时,容易发生比特误码,导致数据帧被丢弃,CRFID需要再次充电重传。目前,后向散射通信普遍使用的EPC Gen2协议是为读取大量标签的少量数据 (标识符) 设计的,但在本文考虑的少量CRFID节点需要传输大量缓存数据的场景下效率较低,不能应对能量捕获条件和信道质量的变化。
针对EPC Gen2协议在移动感知场景下传输大量缓存数据时效率不高的问题,已有文献提出了改进方案。文献[4]提出链路层协议Blink,设计了信道监测算法,通过对丢包率和信号强度的估计自适应调整数据传输速率和选择信道,从而优化吞吐量。文献[5]提出Flit协议,采用突发传输提高信道利用率,采用协调算法降低CRFID间的冲突,相比EPC Gen2协议提高了吞吐量和能量效率。实际上,Blink和Flit这2个协议可以与本文提出方案的配合使用,进一步提高吞吐量。文献[6]与本文的研究动机相似,他们设计了一种特殊的通信协议,将数据帧切割成非常小的数据单元,以适应能量极弱的环境。然而该项工作并没有考虑信道质量较差而发生比特误码及重传的情况,当他们在通过改变帧长最大化吞吐量时,没有考虑包括帧首、帧尾和ACK等控制帧在内的通信开销,而实际上这些通信开销在选择的帧长较短时是不可忽略的。
动态调整帧长和纠删码技术被以往很多文献证明可以在恶劣信道条件下有效增强传输可靠性,提高系统吞吐量。IEEE 802.11标准中采用固定长度的分片阈值,当上层交付的数据超过该阈值则进行分片,该方案显然不能适应动态变化的信道。文献[7]提出根据信道质量动态改变分片阈值,吞吐量得到提高。文献[8]提出一种适用于传感器网络的动态帧长度控制策略,可以降低通信开销,提高能量利用率。文献[9]提出基于纠删码的数据包传输策略SolarCode,通过调整纠删码的编码冗余度来充分利用捕获的过剩能量,从而优化能量利用率和提高数据传输可靠性。文献[10]提出基于Reed-Solomon码的数据收集策略。通过优化传感数据个数、编码冗余度和数据链路层重传次数这几个参数,使得在事先给定的数据收集率和时延约束条件下收集数据的能耗达到最低。上述研究工作表明,动态改变帧长度和编码冗余度能有效适应变化的环境。受此启发,本文在优化EPC Gen2协议传输流程的基础上,提出通过调整帧长、编码冗余度和充电时间提高吞吐量的思想。本文引入突发传输和纠删码对EPC Gen2协议原有流程进行了优化;推导了特定能量捕获条件和信道条件下的有效吞吐量表达式,归纳出有效吞吐量最大化问题,得到帧长、编码冗余度和充电时间理论最优值;提出一种动态帧和充电时间在线调整策略,在运行时根据阅读器端的吞吐量测量反馈调整帧长及编码冗余度;通过仿真得到本文所提方法在不同能量捕获条件和信道条件下采用的帧长、编码冗余度、达到的有效吞吐量和消耗的能量,与EPC Gen2协议固定帧长方案和通过数值分析得到的理论最优值进行了比较。
1 吞吐量优化问题描述 1.1 对EPC Gen2协议流程的改进EPC Gen2协议从读取数据需要经历多个通信周期,传输时延较大,吞吐量较低。本文借鉴了Flit协议针对EPC Gen2通信流程的优化方案,其核心思想是让某个标签在有数据要传输时占用所有的通信时隙进行突发传输。此外,为了应对数据帧的误码情况,本文引入纠删码来减少ACK时延。主要思想是将N个源数据帧编码为成N+M个帧,其中,M为冗余帧个数,每个帧只发送一次,阅读器成功接收任意N个帧就可以解码还原出原始数据,无需对每个帧进行确认;如果数据帧发生误码的次数超过M+1次,则表示数据还原失败。改进后的工作流程如图 1所示。其中,Query、QueryRep命令用于初始化数据请求,设置相关参数。RN16数据帧包含CRFID标签产生的16位随机数,发送给阅读器后阅读器将其作为ACK的一个字段返回给标签,同意标签的数据发送请求。然后标签在每个工作周期根据当前能量捕获条件选择最佳充电时间和连续发送数据帧个数,进行相应的睡眠充电和突发传输,重复上述工作周期操作,直至标签将本轮数据全部发完或等到阅读器返回QueryRep帧,进行下一轮发送请求。
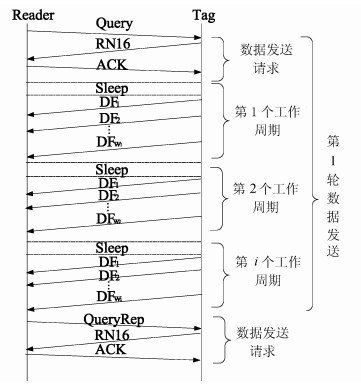 |
| 图1 协议工作流程 Fig. 1 Operating procedure |
1.2 吞吐量分析和优化
CRFID节点的工作周期是一系列充放电过程,如图 2所示,节点休眠一段时间捕获阅读器射频能量,电压上升,电容充电;然后醒来发送数据,电容放电,电压下降。以WISP为例,其CPU工作电压是1.8 V,但是唤醒无线电工作的电压是1.9 V。因此,WISP节点需要充电一段时间,当电压上升至1.9 V,才能唤醒无线电发送数据,当电压降至1.8 V,无线电则会进入休眠状态。充电t时间后的电压U(t) 为:
 |
| 图2 能量捕获过程 Fig. 2 Energy harvesting process |
| $ \begin{array}{l} U\left( t \right) = U\left( 0 \right) + ({U_{{\rm{max}}}}-U\left( 0 \right))(1-{{\rm{e}}^{-t/\tau }}) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ }}U\left( 0 \right){{\rm{e}}^{ - t/\tau }} + {U_{{\rm{max}}}}(1 - {{\rm{e}}^{ - t/\tau }}) \end{array} $ | (1) |
式中,U(0) 表示初始电压值,τ为RC电路时间常数,Umax表示当前能量捕获条件下电容可达到的最大电压。当捕获条件改变时,Umax和τ的值都随之改变。图 3显示了不同能量捕获条件下,随着充电时间增大的电压变化情况。当能量捕获条件较差时,Umax减小,τ增大,使得CRFID节点需要更长的充电时间才能达到无线电工作电压。为了适应不同的能量捕获条件,本文提出让CRFID节点动态选择帧长和充电时间。动态选择帧长的另一个优势是可以适应变化的信道质量。通过联合优化帧长、编码冗余度和充电时间,提高后向散射通信的吞吐量。
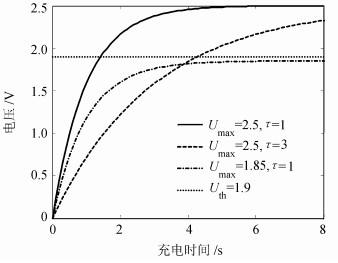 |
| 图3 不同捕获条件下电压随充电时间的变化 Fig. 3 Voltage versus charging time under different harvesting conditions |
首先,推导特定能量捕获条件和信道条件下的有效吞吐量表达式。充电时间为t时,CRFID节点捕获射频能量E(t) 为:
| $ E\left( t \right) = \frac{1}{2}C({U^2}\left( t \right)U_{{\rm{dd}}}^2) $ | (2) |
其中,C是电容大小,Udd为CRFID节点最小工作电压。假设节点发送或接收单位比特数据平均消耗的能量为ebit,用lp和lh分别表示数据帧载荷部分和头部 (包括尾部FCS校验位) 的长度,那么发送一个帧所需的能量为:
| $ {E_{{\rm{frame}}}} = {e_{{\rm{bit}}}} \times ({l_{\rm{p}}} + {l_{\rm{h}}}) $ | (3) |
用wk表示第k个工作周期内突发传输的数据帧个数,由于捕获能量不能小于发送帧所需的能量,有以下不等式成立:
| $ E({t_k}) \ge {w_k}{E_{{\rm{frame}}}} $ | (4) |
根据式 (4) 得到第k个工作周期内突发传输数据帧个数满足以下不等式:
| $ {w_k} \le {\rm{min}}\left\{ {\left\lfloor {\frac{{E({t_k})}}{{{E_{{\rm{frame}}}}}}, N + M-\sum\limits_{i = 1}^{k-1} {{w_i}} } \right\rfloor } \right\} $ | (5) |
式中,
| $ {t_k} \ge-\tau {\rm{ln}}\frac{{\sqrt {2{w_k}{e_{{\rm{bit}}}}({l_{\rm{p}}} + {l_{\rm{h}}})/C + U_{{\rm{dd}}}^2}-{U_{{\rm{max}}}}}}{{{U_{{\rm{dd}}}}-{U_{{\rm{max}}}}}} $ | (6) |
根据式 (6) 可得第k个工作周期内每个帧的平均充电时间为:
| $ {\bar t_k} = \frac{{{t_k}}}{{{w_k}}} $ | (7) |
用pe表示比特误码率,可得一个数据帧的成功传输概率为:
| $ p = {(1{p_e})^{{l_{\rm{p}}} + {l_{\rm{h}}}}} $ | (8) |
按照本文提出的编码策略,N个数据帧发送成功和失败的情况下,期望发送帧个数分别由式 (9) 和式 (10) 表示:
| $ {\psi _{\rm{S}}} = \sum\limits_{i = N-1}^{N + M-1} {\left( {i + 1} \right)} C_i^{N-1}{p^N}{\left( {1 - p} \right)^{i - N + 1}} $ | (9) |
| $ {\rm{ }}{\psi _{\rm{F}}} = \sum\limits_{i = M}^{N + M-1} {\left( {i + 1} \right)} \times C_i^M \times {p^{i-M}} \times {\left( {1-p} \right)^{M + 1}} $ | (10) |
式中,N个数据帧发送成功,实际发帧个数的概率分布满足:
| $ \begin{array}{l} Pr\left\{ {X = z} \right\} = C_{z-1}^{N-1}{\left( {1-p} \right)^{z - N}} \times {p^N}, {\rm{ }}\\ z = N, N + 1, \cdots, N + M \end{array} $ | (11) |
根据式 (11) 的概率分布,可以得到编码后成功收包概率为:
| $ {P_{\rm{s}}} = \sum\limits_{i = N}^{N + M} {C_{i-1}^{N-1}} {\left( {1-p} \right)^{i - N}}{p^N} $ | (12) |
联合式 (5) 和 (7) 可得第k个工作周期的平均时延为:
| $ {D_k} = {w_k}({\bar t_k} + {t_{\rm{f}}}) $ | (13) |
式中,tf为一个帧的传输时延。由此可得有效吞吐量的表达式为:
| $ G = N{l_{\rm{p}}}{P_{\rm{s}}}/\sum\limits_{k = 1}^K {{D_k}} $ | (14) |
式中,K为一轮数据传输经历的周期总数。最后,归纳如下优化问题:
| $ \begin{array}{l} {\rm{max}}G = N{l_{\rm{p}}}{P_{\rm{s}}}/\sum\limits_{k = 1}^K {{D_k}}, \\ {\rm{w}}{\rm{.r}}{\rm{.t}}{\rm{. }}\;\;\;\;\;{l_{\rm{p}}}, M\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\left\{ \begin{array}{l} {t_k} \ge-\tau {\rm{ln}}\frac{{\sqrt {\frac{{2{w_k}{e_{{\rm{bit}}}}({l_{\rm{p}}} + {l_{\rm{h}}})}}{C} + U_{{\rm{dd}}}^2}-{U_{{\rm{max}}}}}}{{{U_{{\rm{dd}}}}-{U_{{\rm{max}}}}}}, \\ \sum\limits_{k = 1}^K {{w_k}} = {\psi _{\rm{F}}} + {\psi _{\rm{S}}} \end{array} \right. \end{array} $ | (15) |
上述优化问题有2个约束条件,第1个约束条件由式 (6) 决定,第2个约束条件表示本轮传输的帧个数与期望传输帧个数相等。数据帧载荷长度lp和编码冗余帧个数M是待优化的变量,这2个变量都有取值范围,其中,数据帧载荷长度lp在EPC Gen2协议中规定取值范围为16~496 bit,并且为16 bit的整数倍,目前设备仅支持96 bit。考虑到传输效率,冗余帧个数也有上限,因此该优化问题的可行解空间为L×Mmax,其中,L为载荷长度的选择空间,Mmax为冗余帧个数的选择空间,理论上可以通过穷举法得到使得吞吐量最大的lp和M的组合。然而在实际中,与能量捕获条件和信道质量相关的参数Umax、τ和pe是动态变化的,需要通过在线估计得到。其中,Umax和τ可以通过跟踪电容的电压得到,而获取pe需要频繁监测信道,会带来额外通信开销,这对于能量匮乏的CRFID系统来说是一个较大的负担。为了减少通信开销,本文提出运行时动态帧和充电时间调整策略DFCTA。
2 动态帧和充电时间调整策略DFCTA 2.1 DFCTA设计思路DFCTA的主要思想是在运行时根据阅读器端的吞吐量测量反馈调整帧长及编码冗余度,控制充电时间,从而提高吞吐量。具体思路如下:CRFID节点周期性跟踪电容的电压,估算Umax和τ值。当CRFID节点移动到阅读器附近且缓存中有数据要发时,从缓存中提取N个长度为lp的源数据帧,编码成N+M个帧,初始帧长设置为16 bit,按照图 1的通信流程与阅读器进行数据传输。阅读器监听接收到的帧,当完成一轮数据传输时,阅读器记录所用时间,得到这段时间内的有效吞吐量,将本轮吞吐量和上一轮进行比较。如果本轮吞吐量相较于上一轮吞吐量提高,则返回ACK告知CRFID节点增加发送帧长度;反之则减少发送帧长度,且每次增加或减少帧长度的单位为8 bit。为了避免频繁更改帧长度,引入调节参数θ(0≤θ≤0.1),如果吞吐量提高或降低的比例不超过θ,则不改变帧长度。同时,CRFID节点在接收到阅读器指定的帧长度后,根据当前能量捕获条件,选择当前工作周期内突发传输的帧个数,发送完毕后进入休眠充电状态,等待下一个工作周期发送数据,直到本轮数据帧全部发完或等到阅读器发送QueryRep帧。在一轮发送结束后,阅读器统计本轮发送成功情况下实际发送冗余帧个数,若发送失败时发送冗余帧个数为M,按照式 (16) 对下一轮冗余帧个数进行更新。
| $ \begin{array}{l} {M_{{\rm{next}}}} = \left\lceil {\left( {1-\alpha } \right) \times {M_{{\rm{avg}}}} + \alpha \times {M_{{\rm{cur}}}} + {M_{{\rm{min}}}}} \right\rceil, \\ \alpha \in \left( {0, 1} \right), {M_{{\rm{next}}}} \in ({M_{{\rm{min}}}}, {M_{{\rm{max}}}}) \end{array} $ | (16) |
式中,Mavg表示历史平均发送冗余帧个数,Mcur表示本轮发送冗余帧个数,Mmin和Mmax分别表示冗余帧个数可取的最小值和最大值,α是权重系数,
具体地,CRFID节点的工作流程如下:
第1步:如果缓存不为空且接收到阅读器的Query或QueryRep帧,返回RN16帧。
第2步:如果接收到阅读器的ACK帧,且ACK中包含与RN16帧相同的16位随机数,则从缓存区提取N个lp长度的源数据,编码成N+M个帧,其中,M和lp的值从阅读器的ACK帧中携带的信息获得。
第3步:工作周期k的初始时刻,跟踪电容电压,估计Umax和τ值。
第4步:根据式 (5) 计算第k个工作周期的最大突发传输帧个数Wk,分别根据式 (7) 和 (6) 计算当前工作周期的最优突发传输帧个数
第5步:充电tkopt时间后,连续发送wkopt个数据帧。如果当前工作周期收到阅读器的QueryRep帧,立即放弃传输,执行第一步;否则,执行第3步,直至将所有N+M个数据帧发送完毕。
阅读器端的工作流程如下:
第1步:发送Query帧,请求CRFID节点数据,如果接收到CRFID节点的RN16帧,返回ACK帧,ACK帧中包含与RN16帧中相同的随机数和CRFID节点接下来传输采用的帧长lp及冗余帧个数M等信息,lp的初始值为16 bit,M的初始值为Mmin。
第2步:缓存数据个数V、正确接收帧个数R和误码帧个数F均置零。
第3步:如果接收到CRFID节点的数据帧,令V=V+lp,如果数据帧正确,令R=R+1;否则,令F=F+1;进一步判断如果R=N,则解码恢复出N个源数据,执行第4步;如果F=M+1,本轮传输失败,执行第4步;否则,继续执行第3步。
第4步:计算本轮有效吞吐量G=V/Δt,其中,Δt为本轮传输时间,由阅读器测量得到,并进行以下操作:如果G>G′(1+θ) 且lp < lpmax,令lp=lp+8;如果G < G′(1-θ) 且lp>lpmin,令lp=lp-8;否则不改变数据帧帧长,其中G′是上一轮有效吞吐量。根据式 (16) 计算下一轮传输的冗余帧个数。
第5步:发送QueryRep帧,请求CRFID节点数据,如果接收到CRFID节点的RN16帧,返回ACK帧,ACK帧中包含与RN16帧中相同的随机数和第4步中计算得到的CRFID节点接下来传输采用的帧长及冗余帧个数等信息,执行第2步。
2.2 帧格式采用的数据帧格式与EPC Gen2协议的数据帧格式相似,如图 4所示。EPC Gen2协议中数据载荷长度是由协议控制 (PC) 字段中的EPC长度字段定义,取值范围为16~496 bit,并且为16 bit的整数倍,因此该字段每位表示16 bit。而由于本文中每次增加或减少帧长度的单位为8 bit,因此修改该字段使得每位表示8 bit,考虑到目前设备仅支持96 bit,取该字段最大值为96 bit,即01100;EPC Gen2协议规定的ACK帧格式由2 bit命令位和16 bit随机数位2个部分组成。然而在本文的算法中,帧长度和冗余帧个数需要根据信道条件和捕获条件来调整,该信息由阅读器通过ACK帧反馈给CRFID节点。因此,额外添加了2个5 bit命令位在ACK中,分别表示下一轮的帧长和冗余帧个数,ACK帧格式如图 5所示。
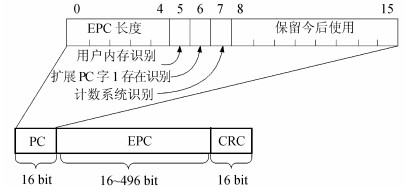 |
| 图4 数据帧格式 Fig. 4 Format of the data frame |
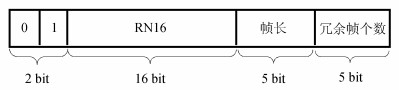 |
| 图5 ACK帧格式 Fig. 5 Format of the ACK frame |
3 性能评价 3.1 信道模型和参数设置
误码率主要取决于接收端的调制方案和信噪比。EPC Gen2协议采用FM0码或Miller码调制技术。图 6显示了Miller码调制的误码率与Eb/N0的函数关系曲线图。其中,Miller码调制的误码率pe可表示为[11]:
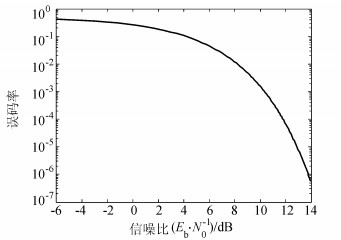 |
| 图6 误码率与Eb/N0的关系 Fig. 6 Bit error rate as a function of Eb/N0 |
| $ {p_{\rm{e}}} = 2Q\left( {\sqrt {\frac{{{E_{\rm{b}}}}}{{{N_0}}}} } \right)[1-Q\left( {\sqrt {\frac{{{E_{\rm{b}}}}}{{{N_0}}}} } \right)] $ | (17) |
式中,
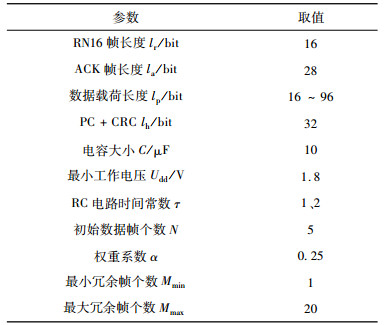
采用的其他仿真设置如表 1所示。
| 表1 仿真参数设置 Tab. 1 Simulation parameters |
 |
3.2 数值分析和仿真实验
假设CRFID节点有6 400 bit缓存数据需要发送给阅读器。对DFCTA策略进行仿真实验,得到吞吐量性能和相应的帧长和冗余帧个数,与用穷举法求解式 (15) 得到的理论最优解及EPC Gen2采用的固定96 bit帧长度策略进行比较。
图 7显示了在Umax=5 V,τ=1的能量捕获条件下,3种方案的吞吐量随信噪比增大的变化情况。随着信噪比增大,吞吐量逐渐升高,最后趋于平稳。图 7中通过穷举法得到的吞吐量理论值大于DFCTA方案和固定帧长方案,但理论值依赖精确的信道质量和充电条件估计,在实际中估计信道质量需要额外的通信开销。本文提出的DFCTA策略无需估计信道质量,通过阅读器对吞吐量的测量值反馈给节点帧长和冗余帧长度,其吞吐量性能接近理论最优值,远高于EPC Gen2协议固定96 bit帧长度的策略。
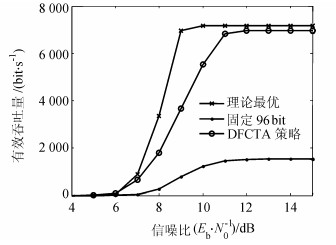 |
| 图7 Umax=5 V、τ=1的能量捕获条件下,3种方案的吞吐量随信噪比增大的变化情况 Fig. 7 Throughput performance of the three schemes under the condition Umax=5 V, τ=1 |
图 8和9分别显示了在与图 7相对应的信噪比条件下,理论方法和DFCTA策略采用的载荷长度和冗余帧个数。
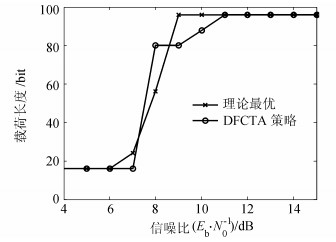 |
| 图8 Umax=5 V、τ=1的能量捕获条件下,载荷长度随信噪比增大的变化情况 Fig. 8 Adopted payload length under the condition Umax=5 V, τ=1 |
 |
| 图9 Umax=5 V、τ=1的能量捕获条件下,冗余帧个数随信噪比增大的变化情况 Fig. 9 Number of redundant frames with increase of Eb/N0 under the condition Umax=5 V, τ=1 |
由图 8、9可以看出,当信噪比较小时,信道质量较差,因此采用的载荷长度较小、冗余帧个数较多;反之当信噪比较大时,采用的载荷长度较大、冗余帧个数较少。提出的DFCTA方案与理论值较为接近,但由于DFCTA方案采用的在线测量吞吐量反馈给节点改变相应的载荷长度和冗余帧个数,曲线存在一定的波动。
图 10~12显示了在Umax=4 V、τ=2的能量捕获条件下,3种方案的吞吐量、载荷长度以及冗余帧个数变化情况。与图 7~9相比,将CRFID节点最大可充电电压下降为4 V,RC电路时间常数τ设置为2,使能量捕获条件降低。总体上,图 10与7相比吞吐量变化情况趋势相同,但是由于能量捕获条件变差,使得总体吞吐量比图 7小。根据图 10和11可以看出,增加帧长并不能无限提高吞吐量。这是因为在信道条件较好,能量捕获条件较差的情况下,充电时间成为了主要影响吞吐量的主要因素。因此,在该条件下,用更长的充电时间的代价来获取更大的发送帧长,可能反而会导致吞吐量下降。
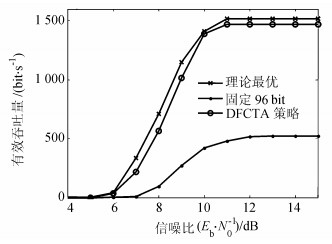 |
| 图10 Umax=4 V、τ=2的能量捕获条件下,3种方案的吞吐量随信噪比增大的变化情况 Fig. 10 Throughput performance of the three schemes with increase of Eb/N0 under the condition Umax=4 V, τ=2 |
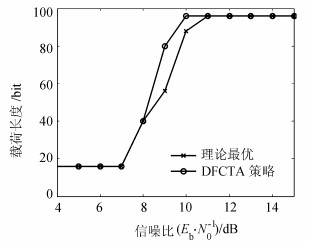 |
| 图11 Umax=4 V、τ=2的能量捕获条件下,载荷长度随信噪比增大的变化情况 Fig. 11 Adopted payload length with increase of Eb/N0 under the ondition Umax=4 V, τ=2 |
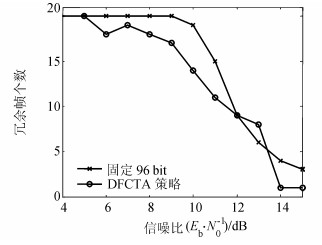 |
| 图12 Umax=4 V、τ=2的能量捕获条件下,冗余帧个数随信噪比增大的变化情况 Fig. 12 Number of redundant frames with increase of Eb/N0 under the condition Umax=4 V, τ=2 |
图 13为DFCTA策略和固定帧长策略在Umax=4 V,τ=2条件下的通信能耗。由图 13可以看出,在信噪比较差的情况下,DFCTA策略比固定帧长策略能耗高,而在信噪比较高的情况下,DFCTA策略能耗较低。这是因为在信噪比较差时,DFCTA策略通过增加冗余包个数保证成功收包率,使得传输量增大;而在信噪比较好时,冗余包个数降低,并且突发传输机制无需每帧返回确认,节省了相应的能耗。值得一提的是本文没有考虑计算能耗,这是因为与通信能耗相比,计算能耗的数量级较小;并且,本文采用的DFCTA策略的核心算法在阅读器端运行,CRFID端计算量较小。总的来说,CRFID节点的能量都是从阅读器捕获,所以能耗指标并非本文关注的重点。
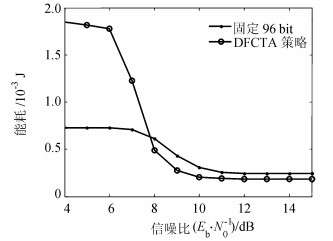 |
| 图13 Umax=4 V、τ=2的能量捕获条件下,通信能耗随信噪比增大的变化情况 Fig. 13 Communication energy consumption under with increase of Eb/N0 the condition Umax=4 V, τ=2 |
图 14给出了不同能量捕获条件下,提出的DFCTA策略的吞吐量性能随信噪比增大的变化。通过改变Umax的值来表征不同的能量捕获条件。从图 14中可以看出在相同信道条件下,随着能量捕获条件提高,吞吐量也随之提高。这是由于当能量捕获条件较好时,充电时间减少,且CRFID节点在一个工作周期能够捕获更多能量来发送更多的数据帧,最终提高吞吐量。
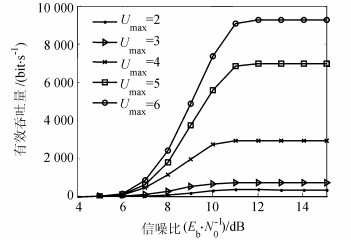 |
| 图14 不同能量捕获条件下吞吐量变化曲线 Fig. 14 Throughput performance under different energy harvesting conditions |
4 结论
提出了一种动态帧和充电时间调整策略DFCTA,根据阅读器端的吞吐量测量反馈调整帧长及编码冗余度,控制充电时间,从而提高吞吐量。仿真结果验证了提出的DFCTA策略相对EPC Gen2协议固定帧长的方案在吞吐量性能上更加优越,且接近理论最优值。本文的研究工作可以使得以后向散射通信方式工作的无源感知网络适应动态变化的能量捕获和信道环境,促进其在移动感知计算领域的应用。
未来的研究工作将考虑进一步考虑多个CRFID节点与阅读器通信的场景下,如何保证数据传输优先级和提高系统吞吐量的问题。
| [1] |
Kim S, Vyas R, Bito J, et al. Ambient RF energy-harvesting technologies for self-sustainable standalone wireless sensor platforms[J]. Proceedings of the IEEE, 2014, 102: 1649-1666. DOI:10.1109/JPROC.2014.2357031 |
| [2] |
Sample A P, Yeager D J, Powledge P S, et al. Design of an RFID-based battery-free programmable sensing platform[J]. IEEE Transactions on Instrumentation and Measurement, 2008, 57(11): 2608-2615. DOI:10.1109/TIM.2008.925019 |
| [3] |
Fu K.UMass Moo:A programmable RFID-scale sensor device[EB/OL].(2015-04-13)[2016-12-24]:https://spqr.eecs.umich.edu/moo/.
|
| [4] |
Zhang P, Gummeson J, Ganesan D.BLINK:A high goodput link layer for backscatter communication[C]//Proceedings of the 10th International Conference on Mobile Systems, Applications, and Services.New York:ACM, 2012:99-112.
|
| [5] |
Gummeson J, Zhang P, Ganesan D.Flit:A bulk transmission protocol for RFID-scale sensors[C]//Proceedings of the 10th International Conference on Mobile Systems, Applications, and Services.New York:ACM, 2012:71-84.
|
| [6] |
Zhang P, Ganesan D.Enabling bit-by-bit backscatter communication in severe energy harvesting environments[C]//Proceedings of the 11th USENIX Conference on Networked Systems Design and Implementation.Seattle:USENIX Association, 2014:345-357.
|
| [7] |
Kim B S, Fang Y, Wong T F, et al. Goodput enhancement through dynamic fragmentation in wireless LANs[J]. IEEE Transactions on Vehicular Technology, 2005, 54(4): 1415-1425. DOI:10.1109/TVT.2005.851361 |
| [8] |
Dong W, Liu X, Chen C, et al. Dynamic packet length control in wireless sensor networks[J]. IEEE Transactions on Wireless Communications, 2014, 13(3): 1172-1181. DOI:10.1109/TWC.2014.012414.121106 |
| [9] |
Yang Y, Su L, Gao Y, et al.SolarCode:Utilizing erasure codes for reliable data delivery in solar-powered wireless sensor networks[C]//Proceedings of the 29th Conference on Information Communications.Piscataway:IEEE, 2010:1-5.
|
| [10] |
Zhu Yihua, Xu Ji, Tian Xianzhong, et al. Energy-efficient low-delay reliable data gathering scheme applying simple Reed-Solomom code for wireless sensor network[J]. Chinese Journal of Computer, 2015, 38(10): 2106-2124. [朱艺华, 徐骥, 田贤忠, 等. 无线传感器网络应用简单Reed-Solomon编码的低能耗和低时延可靠数据收集方案[J]. 计算机学报, 2015, 38(10): 2106-2124.] |
| [11] |
Simon M, Divsalar D. Some interesting observations for certain line codes with application to RFID[J]. IEEE Transactions on Communications, 2006, 54(4): 583-586. DOI:10.1109/TCOMM.2006.873063 |
 2017, Vol. 49
2017, Vol. 49

