2. 北京工商大学 中国化妆品研究中心,北京 100048
2. China Cosmetic Research Centre, Beijing Technol. and Business Univ., Beijing 100048, China
复杂系统运行过程中由于内、外部影响因素众多,属性间的一些非线性关联关系呈现不够显著,阻碍了对系统演化规律及属性间因果关系的认识、理解与利用。对系统的隐性关联性进行识别,有利于及时发现系统的内在本质属性与外在特征属性的关联影响及发展态势,能准确掌握系统运行状况,为合理确定决策措施提供重要依据[1–2]。
在识别复杂系统的关联性过程中,案例及数据的累积具有关键作用。近年来,基于统计数据的分类问题,已卓有成效地应用于多个领域[3–5]。经典的分类方法主要包括:决策树、神经网络、贝叶斯、K近邻算法、判别分析和支持向量机等,概括起来可分为两大类:用于探究指标与类别间分类规则的描述性建模方法;用于预测未知样本类标号的预测性建模方法[6–11]。
决策树作为最典型的描述性建模方法之一,以不断的归纳推理方式将数据分类到不同的分枝,所划分的种类不太多时,可以在总结规则的同时达到较高的分类准确率;但当数据较复杂、划分种类较多时容易出现过拟合导致准确率下降[12]。相反地,当样本量较大、数据较复杂时基于概率统计进行分类的预测性建模方法——贝叶斯算法[13]却可以达到较高的分类准确率。其中应用广泛的朴素贝叶斯算法,在各指标间相互独立的前提下分类效果最好,但不足之处是没有分类规则的输出。
实际应用中由于不同分类算法在分类精度、泛化能力上的差异,为了综合适用条件和关注角度的差异,常采用适当的方法将两种以上的分类算法进行融合以实现优势互补的目的。其中,Chen等[14]在高光谱遥感图像分类领域,提出了一种将遗传算法(GA)与支持向量机(SVM)结合的新颖的子空间优化机制,通过选择不同的子空间来改善RSSE单个支持向量机的精度,从而更好的提高了模型的分类性能。欧阳纯萍等[15]针对中文微博用户的情绪分析问题,提出一种综合朴素贝叶斯、SVM和KNN的分类模型对微博进行细粒度情绪分析,仿真结果表明此种多策略集成方法要好于单一分类方法。徐鹏等[16]为了提高网络入侵检测效果,提出一种基于粒子群和KNN融合方法进行网络入侵检测研究,提高了分类算法的网络入侵检测速度和检测率。
以北京中医药大学王琦教授提出的“肤–体相关论”为依据,期望利用已有的健康医疗案例及数据进一步佐证中医体质对皮肤状态具有决定性作用[17]。已有相关学者进行了研究。其中李建民[18]、王雪[19]等针对体质与单一的皮肤水分、酸碱度以及黑色素、血红素的指标关系进行研究,获得了一些趋势性结论。张慧妍等[20]则利用多属性的皮肤数据,对面部皮肤指标与人体内在的中医体质类型间的隐形关联关系进行了初步探索。
由于人体系统的复杂性,皮肤状态受气候、年龄、睡眠、脏腑等内外因素影响较大,中医体质与皮肤状态关系的定量研究难度较大。近年来随着健康与数据产业的发展,为建立具有良好可解释性与准确性的皮肤–体质分类模型提供了可能。作者基于实测数据,首先在决策树和模糊朴素贝叶斯方法的基础上,通过引入信息融合思路,采用DS证据理论对上述两种模型的分类结果进行融合,充分发挥了小样本条件下决策树良好的归纳特性和大样本条件下贝叶斯分类准确率高的优势。这样,伴随实验数据从少到多的这一动态累积过程,模型参数动态调整以达到最优分类的目的,为智能医疗生态系统构建夯实基础。实证结果表明提出的算法具有很高的分类识别精度与可解释性,可为确定人体外在皮肤指标和内在中医体质类型间的关联性提供科学依据,有利于辅助探索皮肤疾病的发病机制和研发新的治疗方法。
1 决策树和模糊朴素贝叶斯算法描述 1.1 决策树算法描述决策树是一种以实例为基础的归纳学习算法,它着眼于从一组无次序、无规则的事例中推理出决策树表示形式的分类规则[21]。为了快速准确地识别出皮肤与体质间简洁清晰的分类规则,作者在每一个节点上都采用二分分割的CART决策树模型,可将当前样本集分割为两个子样本集,使得生成的决策树总是结构简洁的二叉树。
建立CART决策树模型,首先确定用于分类的指标集和类变量作为训练样本,然后逐一检查每个指标所有可能的划分值,而后将划分按照它们能减少的杂质量来进行排序,求得杂质减少量最大的划分即为最终的划分方式。通常CART决策树中杂质的减少量定义为划分前的Gini指标与划分后的Gini指标之差。对样本集T,其划分前的Gini指标为:
| $Gini(T) = 1 - \sum\limits_{k = 1}^m {p_k^2} $ | (1) |
其中,pk为T中包含类k的概率, m为类别总数。将T划分为2个子集T1和T2,假设样本划分到2个子集的概率分别为
| $Gini{(T)'} = {p_1}' \cdot Gini({T_1}) + {p_2}' \cdot Gini({T_2})$ | (2) |
为了避免CART决策树出现过拟合现象,导致提取出的分类规则冗长而难以理解,进而应用时对未知含噪数据的分类准确度降低,并且出于对运行效率和时间成本的考虑,需要在保证精度的同时对决策树的复杂程度加以控制。因此,定义了一种综合考虑分类能力和决策树规模的改进后剪枝算法,原理如下:
1)分类能力度量
设N为决策树的训练样本总数,n(t)为训练样本中进入到决策树节点t的实例个数,e(t)为训练样本中到达节点t并且属于节点t所对应的类别的实例总数,定义决策树的分类精度为:
| $a(M) = \sum\limits_{t = 1}^M {\frac{{e(t)}}{{n(t)}} \times \frac{{n(t)}}{N}} $ | (3) |
其中,M为决策树中所有叶结点的个数,a(M)的值越大,分类效果越明显,决策树的分类性能就越好。
2)决策树规模度量
根据经验,决策树叶结点数保持在5~10个时分类效果最理想,小于2个或大于25个时,实际应用效果较差[22]。因此若决策树的叶结点个数为M,则定义决策树的规模系数为:
| $d(M) = \left\{ \begin{array}{l}0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;M < 2{\text{或}}M > 25;\\(M - 2)/(5 - 2),\;\;\;\;\;\;\;\;2 \le M < 5;\\1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;5 \le M \le 10;\\(25 - M)/(25 - 10),\;\;\;\;10 < M \le 25\end{array} \right.$ | (4) |
可见,d(M)的值越大,决策树的复杂程度越小,抽取出来的规则也越容易理解和应用。
3)改进后剪枝算法
为了综合考虑决策树模型的分类能力和树的规模,本文定义了基于决策树分类精度a(M)和规模系数d(M)的最优树评价指标I(M),计算公式为:
| $I(M) = {k_1} \cdot a(M) + {k_2} \cdot d(M)$ | (5) |
其中,k1、k2分别为分类精度和规模系数的权重,满足k1+k2=1,k1>0,k2>0。对从原始决策树中裁剪出的一系列候选子树,分别比较各个树的最优树评价指标I(M),I(M)值最大的一棵即为最终的最优决策树。
1.2 模糊朴素贝叶斯算法描述朴素贝叶斯为基于贝叶斯定理将直观的知识表示形式与概率理论有机结合的分类学习方法,是模式分类中进行不确定性推理建模的有效工具[23]。其中,指标集X属于类别Yk的概率为:
| $\begin{aligned}[b]P({Y_k}|X) = & \frac{\displaystyle{P({X_1},{X_2}, \cdots ,{X_n}|{Y_k}) \cdot P({Y_k})}}{\displaystyle {P({X_1},{X_2}, \cdots ,{X_n})}} = \\[5pt]& \frac{\displaystyle {P({Y_k}) \cdot \prod\limits_{j = 1}^n {P({X_j}|{Y_k})} }}{\displaystyle {P({X_1},{X_2}, \cdots ,{X_n})}}\end{aligned}$ | (6) |
由于联合概率
建立朴素贝叶斯模型,首先应通过统计分析确定类别Yk的先验概率P(Yk),然后计算各个类别下指标Xj的模糊条件概率
| $\widetilde P({X_j}|{Y_k}) = \sum\limits_{i = 1}^q {{\mu _i}} /{m_k},i = 1,2, \cdots ,q$ | (7) |
其中,mk为属于类别Yk的样本总数,μi为Yk类别下指标Xj落在某一区间内的各个样本对区间的模糊隶属度,q为落在该区间的样本总数。
 |
| 图1 指标对区间的模糊隶属度函数 Fig. 1 Fuzzy membership function of index to interval |
按照上述原理逐一计算各类体质下指标的模糊条件概率,步骤如下:
1)所有皮肤指标数据归一化,确保各指标的区间范围为[0, 1];
2)将区间[0,1]等距划分为5个边界有重叠的子区间,构建指标对区间的模糊隶属度函数;
3)计算体质为Yk的样本中各指标下的每个样本值分别对5个子区间的模糊隶属度;
4)计算Yk体质下各指标对5个子区间的模糊条件概率,并列出模糊条件概率表;
5)重复步骤3)和4),逐一计算出各类体质下样本的模糊条件概率,同样列出相应的模糊条件概率表。
这样,得出各体质确定条件下皮肤指标的模糊条件概率后,将其与此前计算出的先验概率相乘,求得的最大后验概率对应的体质类型即为模糊朴素贝叶斯模型的输出结果。
2 中医体质分类信息融合模型目前信息融合方法很多,例如加权平均法、多贝叶斯估计法、证据推理方法和模糊逻辑等。其中,DS证据理论是信息融合最经典的算法之一[24]。采用DS证据理论将决策树和模糊朴素贝叶斯模型的分类结果进行融合,以在保留两者各自优势的同时得到更好的分类准确率。具体建模步骤如下:
首先分别建立基于后剪枝CART决策树和模糊朴素贝叶斯的中医体质分类模型,依据两模型得到的体质类型分类结果定义融合识别框架为
| $P{({Y_k}|X)_{\rm CART}} = \left\{ \begin{array}{l}{b_k},\begin{array}{*{20}{c}}{} & {k = t;}\end{array}\\1 - {b_k}/(m - 1),k \ne t\end{array} \right.$ | (8) |
其中,
于是可得决策树模型对各体质的分类概率
| $\begin{array}{l}m(C) = \frac{\displaystyle{\sum\limits_{{F_i} \cap {F_j} = C} {{m_1}({F_i}) \cdot {m_2}({F_j})} }}{\displaystyle{1 - \sum\limits_{{F_i} \cap {F_j} = \Phi } {{m_1}({F_i}) \cdot {m_2}({F_j})} }}\end{array}$ | (9) |
式中:
根据皮肤领域背景知识,结合中医理论,从紧实度、白皙度、水润度、平滑度等角度确定下能够充分全面衡量人体面部皮肤状态的17个皮肤指标,构建综合性较强的多维人体面部皮肤指标体系如图2所示。并于2014年11月在北京工商大学化妆品协同中心实验室采用专业的皮肤测试仪器对多名志愿者的上述皮肤指标进行测试,每名志愿者分别测试额头、左眼角、左脸颊和下巴4个部位。此次测试对象主要为京津冀地区年龄属于18~35岁之间的女性,体质分类结果由中医专家根据中医体质问卷调查表确定。
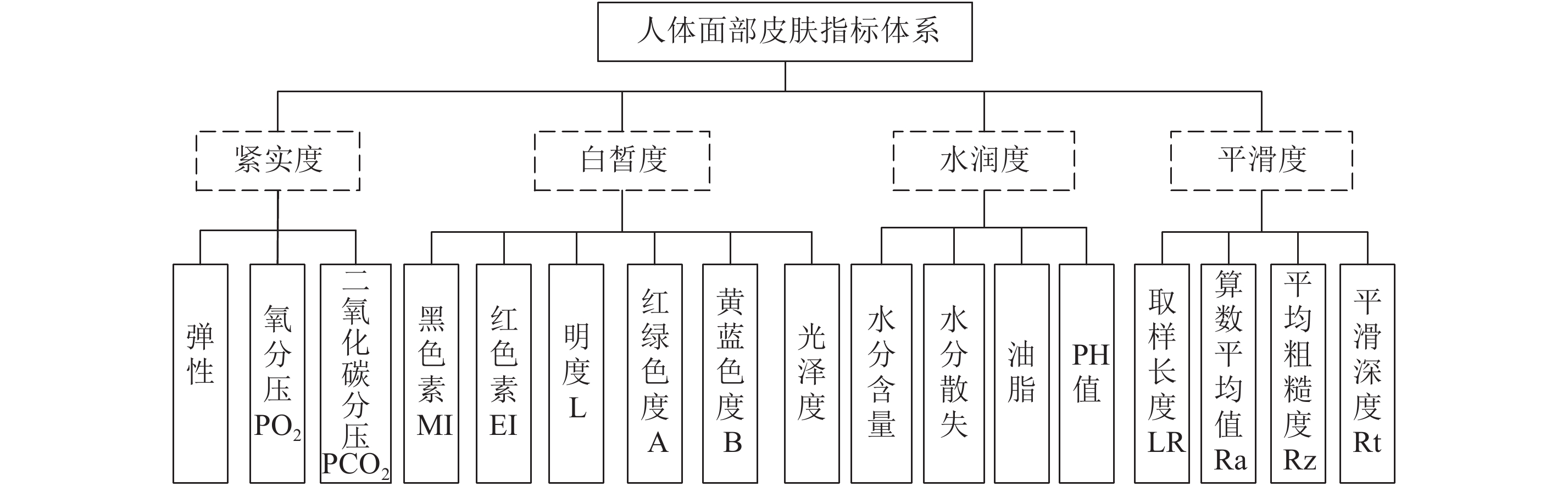 |
| 图2 人体面部皮肤指标体系 Fig. 2 Index system of human facial skin |
根据专家意见采用层次分析法分别计算测试部位的权重,结果见表1。
| 表1 层次分析法赋权结果 Tab. 1 Results of AHP weighting |
 |
为避免皮肤指标体系包含冗余属性影响建模精度,在构建中医体质分类模型前首先采用主成分分析法进行降维,转化为8个综合指标[25]。而后为了测试本文模型的有效性,先随机选取151组样本数据作为建模用训练样本,余下30组为测试样本;对照组的小规模建模数据则从151组样本中采用轮盘赌的方式抽取了80组,测试的30组样本不变。
3.2 实验仿真与结果依据中医理论,人体有平和质、气虚质、阳虚质、阴虚质等九大体质,不同的体质在皮肤上的表征各有不同。平和质的人群属于健康人群,而其他八种属于偏颇体质的人群均存在某些方面的健康问题,或多或少的会在面部皮肤指标上有所体现。统计数据表明,阳虚质是当前社会所有偏颇体质中最常见的体质之一,多产生于不良的生活习惯如:熬夜、贪凉、过度控制饮食以及长期大量服用抗生素等。通过中医治疗并配合适当的锻炼、健康的饮食,阳虚质人群可以逐渐调理达到和平和质人群一样的健康状态。因此考虑到阳虚质的广泛性且易于改善的特点,本文将其单独提出来作为一个研究的大类,依据皮肤指标对平和质、阳虚质和其它偏颇质进行分类研究。
针对151名测试者的分类模型构建是先基于样本数据构建出分类精度为84%,叶节点个数为23的CART决策树模型。为了降低决策树的复杂度、提高泛化能力,防止出现过拟合现象,从原始的决策树中裁剪出了3颗候选子树,参照式(3)~(5)分别计算这3颗候选子树的最优树评价指标I(M)。由于研究初期没有特殊的倾向性考虑,默认式(5)中k1=k2=0.5。保留计算出的I(M)值最大的一棵作为最终的最优决策树,此时决策树的分类精度为75%,包含10个叶结点。
然后建立模糊朴素贝叶斯分类模型,设3种体质类型分别为贝叶斯模型的3个类变量,
| 表2 平和体质模糊条件概率 Tab. 2 Fuzzy conditional probability of yin-yang harmony constitution |
 |
训练样本的统计分析表明,151组样本中,包含平和体质47组,阳虚体质42组,其他偏颇体质62组。除以总样本数可以求出3类体质的先验概率分别为31.1%,27.8%和41.1%。将上述计算结果带入式(6),逐一计算出151个训练样本的分类输出,将分类结果与专家诊断结果相对比,分类正确率达到72%。
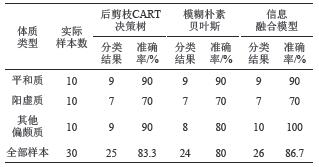
可见,单独使用CART决策树模型和模糊朴素贝叶斯模型对训练样本分类,准确率分别为75%和72%,其中决策树模型对3类体质分别的训练准确率b1,b2,b3为76.6%、61%和81.1%。将上述结果带入式(8)~(9),建立融合的分类模型,对现存的30组测试样本进行测试,可发现通过DS证据理论融合后的算法分类准确度达到86.7%,明显高于单独使用CART决策树模型的83.3%和模糊朴素贝叶斯模型的80%,其中分类模型的详细输出见表3。
| 表3 分类模型测试输出结果 Tab. 3 Results of classification model test output |
 |
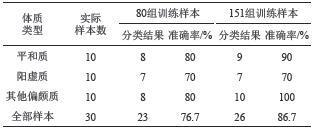
针对80名测试者进行的小规模对照组分类建模实验,采用类似的流程,将决策树和朴素贝叶斯的后验概率带入到DS证据融合公式求取最大联合信任度,随着训练样本量的变化,改进后剪枝决策树算法及模糊朴素贝叶斯算法的分类精度分别为73.3%和70%,且对应的D-S证据理论中两模型的信任函数动态变化,导致联合证据信任度变化,最终测试分类准确率输出结果见表4。
| 表4 分类模型动态测试输出结果 Tab. 4 Results of classification model dynamic test output |
 |
可见,本文提出的基于关联性识别的动态分类模型,应用在皮肤与中医体质分类判别研究中,可通过案例数据的应用,实证皮肤状态与中医体质间具有较强的关联关系,且具有较好的依据实测数据动态调整模型参数的功能。研究结果不仅与中医理论相吻合,且随着数据获取量的增大分类精度与专家评定结果吻合度会逐步提高,为后续基于大数据的皮肤–体质健康领域研究工作的开展提供了可借鉴的思路。
此外,通过分析剪枝后的决策树模型,可以发现气血(氧分压)、色泽、弹性、水分含量等指标对体质类别的影响较大,这些指标所表征的皮肤状态的提高直接导致内在体质状态的改善;相反的,当这些指标低于某个临界值时则表明体质状态不良,甚至会出现由平和体质向偏颇体质转化的可能,表明模型具有良好的可解释性与关联知识发现的能力。
4 结 论基于复杂系统多个属性间的关联关系识别构建分类模型,对于探究系统运行机制,间接检测及预测、决策研究具有重要意义。
针对需要兼顾可解释性与准确性的分类要求,提出一种基于DS证据理论融合后剪枝CART决策树与模糊朴素贝叶斯模型的中医体质优化分类方法,不仅充分发挥了小样本条件下决策树对指标与类关系的良好归纳特性与大样本条件下模糊朴素贝叶斯分类准确率较高的优势;而且针对案例或数据的不断积累,可以通过调整模型权重实现动态优化分类模型的目的。
实验结果表明,对同一的测试样本组进行测试,本文提出的融合模型的分类准确率较两个单独使用的模型更高,且具有较好的可解释性与知识发现能力。
| [1] |
Li Tingyu, Gan Fangji, Wan Zhengjun. Method for defect classification based on SVM and current drag effect[J]. Journal of Sichuan University(Engineering Science Edition), 2015, 47(6): 172-178. [李宇庭, 甘芳吉, 万正军. 基于SVM及电流牵扯效应的金属缺陷分类识别方法[J]. 四川大学学报(工程科学版), 2015, 47(6): 172-178.] |
| [2] |
Krishnan B, Vlachos I, Faith A. A novel spatiotemporal analysis of peri-ictal spiking to probe the relation of spikes and seizures in epilepsy[J]. Annals of Biomedical Engineering, 2014, 42(8): 1606-1617. DOI:10.1007/s10439-014-1004-x |
| [3] |
Gomathi S,Narayani V.Monitoring of lupus disease using decision tree induction classification algorithm[C]//International Conference on Advanced Computing and Communication Systems. Coimbatore, INDIA: IEEE,2015.
|
| [4] |
Pal R, Kupka K, Aneja A P. Business health characterization: A hybrid regression and support vector machine analysis[J]. Expert Systems with Applications, 2016, 49: 410-418. |
| [5] |
数据挖掘导论[M].范明,范宏建,译.2版.北京:人民邮电出版社,2011:89–92.
|
| [6] |
Zhao Shu, Chen Rui, Zhang Yanping. MICkNN:Multi-Instance Covering KNN Algorithm[J]. Tsinghua Science & Technology, 2013, 18(4): 360-368. |
| [7] |
Priya T, Prasad S, Wu Hao. Superpixels for spatially reinforced bayesian classification of hyperspectral images[J]. Geoscience & Remote Sensing Letters IEEE, 2015, 12(5): 1071-1075. |
| [8] |
Petersen J, Austin D, Sack R. Actigraphy-based scratch detection using logistic regression[J]. IEEE Journal of Biomedical & Health Informatics, 2013, 17(2): 277-283. |
| [9] |
Zhang Weifeng, Chen Xingshu, Yin Xueyuan. A novel data cleaning approach for web usage mining[J]. Journal of Sichuan University(Engineering Science Edition), 2014, 46(增刊1): 160-165. [张峰伟, 陈兴蜀, 尹学渊. 一种Web使用挖掘数据清理方法[J]. 四川大学学报(工程科学版), 2014, 46(增刊1): 160-165.] |
| [10] |
Wu Jiansheng, Zhou Zhihua. Sequence-based prediction of microRNA-Binding residues in proteins using cost-sensitive laplacian support vector machines[J]. IEEE/ACM Transactions on Computational Biology & Bioinformatics, 2013, 10(3): 752-759. |
| [11] |
Zhang Fuzhi, Zhou Quanqiang. Ensemble detection model for profile injection attacks in collaborative recommender systems based on BP neural network[J]. Information Security Iet, 2015, 9(1): 24-31. DOI:10.1049/iet-ifs.2013.0145 |
| [12] |
Xu Peng, Zhang Yanjiang, Su Sen. Research on resource scheduling of PaaS[J]. Journal of Huazhong University of Science and Techuology(Natural Science Edition), 2013, 41(S2): 52-56. [徐鹏, 张岩江, 苏森. PaaS云资源调度技术研究[J]. 华中科技大学学报(自然科学版), 2013, 41(S2): 52-56.] |
| [13] |
Ji Junzhong, Zhang Lingling, Wu Chensheng. Semantic weight-based naïve bayesian algorithm for text sentiment classfication[J]. Journal of Beijing University of Technology, 2014, 40(12): 1884-1890. [冀俊忠, 张玲玲, 吴晨生. 基于知识语义权重特征的朴素贝叶斯情感分类算法[J]. 北京工业大学学报, 2014, 40(12): 1884-1890.] |
| [14] |
Chen Y, Zhao X, Lin Z. Optimizing subspace SVM ensemble for hyperspectral imagery classification[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2014, 7(4): 1295-1305. |
| [15] |
Ouyang Chunping, Yang Xiaohua, Lei Longyan. Multi-strategy approach for fine-grained sentiment analysis of chinese microblog[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2014, 50(1): 67-72. [欧阳纯萍, 阳小华, 雷龙艳. 多策略中文微博细粒度情绪分析研究[J]. 北京大学学报(自然科学版), 2014, 50(1): 67-72.] |
| [16] |
Xu Peng, Jiang Fengru. Network intrusion detection model based on particle swarm optimization and k-nearest neighbor[J]. Computer Engineering and Applications, 2014, 50(11): 95-98. [徐鹏, 姜凤茹. 粒子群算法和K近邻相融合的网络入侵检测[J]. 计算机工程与应用, 2014, 50(11): 95-98. DOI:10.3778/j.issn.1002-8331.1206-0445] |
| [17] |
Wang Ji, Zhang Huimin, Li Lingru. Theory of skin relating to constitution put forward by Professor Wang Qi and its application in detmatology[J]. Journal of Beijing University of Traditional Chinese Medicine, 2013, 36(7): 476-477. [王济, 张惠敏, 李玲孺. 王琦教授肤-体相关论的提出及其在皮肤病诊疗中的应用[J]. 北京中医药大学学报, 2013, 36(7): 476-477.] |
| [18] |
Li Jianmin, Wang Xue, Qi Yonghua. Study on the relationship between traditional Chinese medicine con-stitution and skin’s water, pH value[J]. Acta Chinese Medicine and Pharmacology, 2012, 40(4): 81-82. [李建民, 王雪, 祁永华. 中医体质与皮肤水分及pH值的关系研究[J]. 中医药学报, 2012, 40(4): 81-82.] |
| [19] |
Wang Xue, Xu Yanming, Zhang Nin. Study on the relationship between traditional Chinese medicine con-stitution and skin's melanin, protoheme[J]. Chinese Journal of Aesthetic Medicine, 2012, 21(5): 764-766. [王雪, 徐艳明, 张宁. 中医体质与皮肤黑色素和血红素的关系研究[J]. 中国美容医学, 2012, 21(5): 764-766.] |
| [20] |
Li Shuang, Zhang Huiyan, Wang Li. Fuzzy optimization classification in TCM constitution based on multi-attrinute skin indexes[J]. Journal of Frontiers of Computer Science and Technology, 2016, 10(7): 995-1002. [李爽, 张慧妍, 王立. 多属性皮肤指标的中医体质模糊优化分类模型[J]. 计算机科学与探索, 2016, 10(7): 995-1002.] |
| [21] |
Breiman L,Friedman J,Olshen R A,et al.Classfication and regression trees[M].Belmont:Wadsworth,1984,1-358.
|
| [22] |
Dumitrescu S, Wu Xiaolin. A new framework of LSB steganalysis of digital media[J]. IEEE Transactions On Signal Processing, 2005, 53(10): 3936-3947. DOI:10.1109/TSP.2005.855078 |
| [23] |
Zhang Jun, Chen Chao, Xiang Yang. Internet traffic classification by aggregating correlated naive bayes predictions[J]. IEEE Transactions on Information Forensics & Security, 2013, 8(1): 5-15. |
| [24] |
Dong Gangfang, Kuang Gangyao. Target recognition via information aggregation through dempster-shafer’s evidence theory[J]. IEEE Geoscience & Remote Sensing Letters, 2015, 12(6): 1247-1251. |
| [25] |
Chen Chao.Intelligent modelling based on analysis and process of redundant problems and its application[D].Shanghai:East China University of Science and Technology,2015. [陈超.智能建模中冗余问题的分析与处理及其应用[D].上海:华东理工大学,2015]
|
 2017, Vol. 49
2017, Vol. 49

