波达方向(direction of arrival, DOA)估计是阵列信号处理领域研究的重要内容之一,在雷达、通信、电子对抗等领域都有着广泛的应用。随着现代电磁环境的日益复杂,欠定DOA估计(信号数多于阵元数)问题越来越常见,如何利用有限的阵元实现对尽可能多的信号进行DOA估计成为目前研究的热点问题。
最近,互质阵列[1]的提出为解决欠定DOA估计问题提供了一个新的思路。由于其具有易于构造、阵列扩展性好、物理阵列和虚拟阵元具有解析表达式等优点受到国内外研究者的广泛关注[2–11]。现有成果可分为两大类:一是,子空间类方法[1–2],该方法的不足在于仅能够利用差联合阵列中连续的虚拟阵元部分而舍弃了非连续部分的虚拟阵元,导致阵列的虚拟孔径存在一定的损失同时估计精度会受到扫描网格的影响。二是,基于稀疏重构的方法[4–8],该方法虽然克服了传统子空间方法的不足,但其假设所有的目标准确地位于预定的字典网格上,实际环境中并不一定满足即存在基不匹配问题[10],此时估计性能会严重下降。虽然字典网格越密集,实际DOA与字典网格之间的误差会越小,但计算量也会随之增加同时过密集的网格会造成字典原子之间的相关性增强,从而影响重构的性能。文献[11]通过利用原始信号和网格失配的联合稀疏,在DOA估计中采用1阶泰勒级数展开来逼近网格误差,但仍然受高阶模型误差的影响。文献[12]利用阵列运动的方式获得与空缺项相对应的测量值,然而该方法对阵列的运动状态有着严格要求,在实际的应用中受限。文献[13]通过引入额外的工作频率来实现对空洞的填充,但额外频率的使用会增加系统的工作带宽同时会引入信号源特性起伏,从而在一定程度上增加了系统复杂度和DOA估计误差。文献[14]将基于稀疏重构的外推技术用于对差联合阵列中空洞部分的填充,但该方法的估计性能同样受到基不匹配的影响,在实际应用中效果不理想。
本文将矩阵填充理论[15–22]引入到互质阵列DOA估计当中,提出了一种基于不动点求根多重分类方法(fixed point continuous root multiple signal classification, FPC-root-MUSIC)。首先根据差联合阵列与波程差一一对应的特性,对阵列输出协方差矩阵进行扩展得到一个Toeplitz化的协方差矩阵,然后利用不定点延续算法将协方差矩阵的零元素进行填充恢复为完整的协方差矩阵,最后利用求根MUSIC方法进行DOA估计。与现有方法相比,该方法提高了可估计信号的数目同时能够有效避免稀疏重构算法中基不匹配的影响,具有较好的估计精度和分辨力。
1 互质阵列模型互质阵列结构如图1所示,由两个不同的均匀子阵组成。
图1中,子阵1包含有N个物理阵元,各阵元位置位于
 |
| 图1 互质阵列结构 Fig. 1 Structure of coprime array |
假设K个远场窄带信号分别以
| $\mathit{\boldsymbol{X}}(t) = \mathit{\boldsymbol{As}}(t) + \mathit{\boldsymbol{n}}(t)$ | (1) |
式中:
| $A(i,j) = {{\rm e} ^{{\rm{j}}2{{\text{π} }}{d_i}\sin {\theta _j}/\lambda }}$ | (2) |
式中,di为第i个物理阵元的位置。
假设各入射信号之间互不相关,噪声为高斯白噪声且与信号之间相互独立。则阵列接收数据的协方差矩阵可表示为:
| ${\mathit{\boldsymbol{R}}_{X}} = E[\mathit{\boldsymbol{X}}(t){\mathit{\boldsymbol{X}}^{\rm H}}(t)] = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{R}}_{s}}{\mathit{\boldsymbol{A}}^{\rm H}} + \mathit{\boldsymbol{n}}$ | (3) |
式中:
在实际应用中,由于快拍数L有限,
| ${\overline{R}_{X}} = (1/L)\sum\limits_{t = 1}^L {\mathit{\boldsymbol{X}}(t){\mathit{\boldsymbol{X}}^{\rm H}}(t)} $ | (4) |
首先,给出差联合阵列(difference coarray)的定义,定义如下集合:
| $D = \{ {d_i} - {d_j}\} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {d_i},{d_j} \in C$ | (5) |
式中,C为所有阵元位置集合,D为阵列中所有阵元位置差值构成的集合。由于集合D中存在冗余元素,定义集合D中所有不同元素组成的集合Du为差联合阵列。集合Du中的元素du在集合D中出现的次数为权值系数
图1所示的互质阵列相对应的差联合阵列如图2所示,虚拟阵元的位置具体可表示为:
| $\begin{aligned}& \quad\quad S = \{ \pm (nMd - mNd)\} ,\\& 0 \le n \le N - 1,0 \le m \le 2M - 1\end{aligned}$ | (6) |
根据图2所示虚拟阵元的分布可知,互质阵列的差联合阵列被划分为1个均匀阵列和2个非均匀阵列,均匀阵列中
 |
| 图2 差联合阵列结构 Fig. 2 Structure of difference coarray |
对于互质阵列而言,各集合包含元素的个数分别为:
| $\left\{\!\!\!\! \begin{array}{l}{\rm card}(C) = N + 2M - 1,\\{\rm card}({D_u}) = 3MN + M - N,\\{\rm card}(\varPsi) = 2MN + 2M - 1,\\{\rm card}(\varGamma) = 4MN - 2N + 1\end{array} \right.$ | (7) |
式中,
由于MUSIC方法需要进行空间平滑处理,其仅能利用连续的2MN+2M–1个虚拟阵元数,可估计的最大信号数由均匀自由度F决定,即
| $F = (\left| C \right| - 1)/2 = o(MN)$ | (8) |
而未得到有效利用的虚拟阵元数为
对于图1所示的互质阵列,阵列输出数据协方差矩阵
| $\begin{aligned}[b]{\mathit{\boldsymbol{R}}_{\mathit{\boldsymbol{X}}}} = & \left| {\begin{array}{*{20}{c}}{\displaystyle\sum\limits_{k = 1}^K {p_k^2} }&{\displaystyle\sum\limits_{k = 1}^K {p_k^2{{\rm e}^{\mathit{\boldsymbol{ - }}{\rm j}O}}} }& \cdots &{\displaystyle\sum\limits_{k = 1}^K {p_k^2{{\rm e}^{\mathit{\boldsymbol{ - }}{\rm j}P}}} }\\{\displaystyle\sum\limits_{k = 1}^K {p_k^2{{\rm e}^{{\rm j}O}}} }&{\displaystyle\sum\limits_{k = 1}^K {p_k^2} }& \cdots &{\displaystyle\sum\limits_{k = 1}^K {p_k^2{{\rm e}^{\mathit{\boldsymbol{ - }}{\rm j}Q}}} }\\ \vdots & \vdots &{}& \vdots \\{\displaystyle\sum\limits_{k = 1}^K {p_k^2{{\rm e}^{{\rm j}P}}} }&{\displaystyle\sum\limits_{k = 1}^K {p_k^2{{\rm e}^{{\rm j}Q}}} }& \cdots &{\displaystyle\sum\limits_{k = 1}^K {p_k^2} }\end{array}} \right| + \mathit{\boldsymbol{n}}{\kern 1pt} = \\& \left| {\begin{array}{*{20}{c}}{R(0)}&{R( - M)}& \cdots &{R( - (2M - 1)N)}\\{R(M)}&{R(0)}& \cdots &{R(M - (2M - 1)N)}\\ \vdots & \vdots &{}& \vdots \\{R((2M - 1)N)}&{R((2M - 1)N - M)}& \cdots &{R(0)}\end{array}} \right| + \mathit{\boldsymbol{n}}\end{aligned}$ | (9) |
式中:
| ${D_u} = \{ - (2M - 1)N, \cdots ,0, \cdots ,(2M - 1)N\} $ | (10) |
由此可见,差联合阵列与阵列所能得到的波程差是一一对应的。
在实际应用中,由于受到信噪比和快拍数有限的影响,式(9)协方差矩阵中同一波程差对应的元素并不完全相等,因此,为了充分利用样本信息,对相同波程差的元素进行求平均运算作为该波程差对应的输出值,即
| $\hat{R}({d_u}) = \frac{1}{{w({d_u})}}\sum\limits_{i = 1}^{w({d_u})} {{R_i}({d_u})} $ | (11) |
式中,
进一步根据波程差与差联合阵列一一对应的特性,对协方差矩阵
| ${R_{\rm T}}(i,j) = \left\{ \!\!\!\! \begin{array}{l}\hat R({d_u}), {\kern 1pt} i - j = {\kern 1pt} {d_u};\\[10pt]0,{\kern 1pt} {\kern 1pt} {\kern 1pt} \text{其他}\end{array} \right.$ | (12) |
例如,对于阵元数为6的互质阵列,其中,M=2,N=3,
| ${\mathit{\boldsymbol{R}}_{\mathit{\boldsymbol{X}}}} = \left[ {\begin{array}{*{20}{c}}{R(0)}&{R( - 2)}&{R( - 3)}&{R( - 4)}&{R( - 6)}&{R( - 9)}\\[3pt]{R(2)}&{R(0)}&{R( - 1)}&{R( - 2)}&{R( - 4)}&{R( - 7)}\\[3pt]{R(3)}&{R(1)}&{R(0)}&{R( - 1)}&{R( - 3)}&{R( - 6)}\\[3pt]{R(4)}&{R(2)}&{R(1)}&{R(0)}&{R( - 2)}&{R( - 5)}\\[3pt]{R(6)}&{R(4)}&{R(3)}&{R(2)}&{R(0)}&{R( - 3)}\\[3pt]{R(9)}&{R(7)}&{R(6)}&{R(5)}&{R(3)}&{R(0)}\end{array}} \right]$ | (13) |
| ${\mathit{\boldsymbol{R}}_{\rm T}} = \left[ {\begin{array}{*{20}{c}}{R(0)}&{R( - 1)}&{R( - 2)}&{R( - 3)}&{R( - 4)}&{R( - 5)}&{R( - 6)}&{R( - 7)}&0&{R( - 9)}\\[3pt]{R(1)}&{R(0)}&{R( - 1)}&{R( - 2)}&{R( - 3)}&{R( - 4)}&{R( - 5)}&{R( - 6)}&{R( - 7)}&0\\[3pt]{R(2)}&{R(1)}&{R(0)}&{R( - 1)}&{R( - 2)}&{R( - 3)}&{R( - 4)}&{R( - 5)}&{R( - 6)}&{R( - 7)}\\[3pt]{R(3)}&{R(2)}&{R(1)}&{R(0)}&{R( - 1)}&{R( - 2)}&{R( - 3)}&{R( - 4)}&{R( - 5)}&{R( - 6)}\\[3pt]{R(4)}&{R(3)}&{R(2)}&{R(1)}&{R(0)}&{R( - 1)}&{R( - 2)}&{R( - 3)}&{R( - 4)}&{R( - 5)}\\[3pt]{R(5)}&{R(4)}&{R(3)}&{R(2)}&{R(1)}&{R(0)}&{R( - 1)}&{R( - 2)}&{R( - 3)}&{R( - 4)}\\[3pt]{R(6)}&{R(5)}&{R(4)}&{R(3)}&{R(2)}&{R(1)}&{R(0)}&{R( - 1)}&{R( - 2)}&{R( - 3)}\\[3pt]{R(7)}&{R(6)}&{R(5)}&{R(4)}&{R(3)}&{R(2)}&{R(1)}&{R(0)}&{R( - 1)}&{R( - 2)}\\[2pt]0&{R(7)}&{R(6)}&{R(5)}&{R(4)}&{R(3)}&{R(2)}&{R(1)}&{R(0)}&{R( - 1)}\\[3pt]{R(9)}&0&{R(7)}&{R(6)}&{R(5)}&{R(4)}&{R(3)}&{R(2)}&{R(1)}&{R(0)}\end{array}} \right]$ | (14) |
由式(14)可知,
| $\begin{aligned}& \min \ {\rm rank}({\mathit{\boldsymbol{R}}_{\rm c}})\\& {\rm s.t}. \ {P_\varOmega }{\kern 1pt} ({\mathit{\boldsymbol{R}}_{\rm c}}) = {P_\varOmega }({\mathit{\boldsymbol{R}}_{\rm T}})\end{aligned}$ | (15) |
式中,
| $\mathit{\boldsymbol{Null}}({P_\varOmega }) = \{ \varPhi \in {\mathit{\boldsymbol{R}}^{|\varGamma | \times |\varGamma |}}:{P_\varOmega }(\varPhi ) = \mathit{\boldsymbol{O}}\} $ | (16) |
式中,O为零向量。在零空间内的矩阵是难以恢复的,而矩阵Rc等同于一个扩展的均匀线阵协方差矩阵。其任意元素都是非零的,故采样算子的零空间为空集,无论采用何种采样算子,Rc都不在采样算子的零空间中满足NSP。因此,可采用矩阵填充算法将扩展的协方差矩阵恢复为完整的阵列输出协方差矩阵。
针对上述问题,作者提出了FPC-root-MUSIC方法。首先,通过矩阵填充算法对扩展的阵列输出协方差矩阵进行恢复;然后,利用root-MUSIC方法实现对入射信号DOA的估计。
由于直接求解秩最小化问题是一个NP难问题,这里通过凸松弛的方法,利用核范数最小化对秩最小化进行等效。因此,式(15)转化为如下形式:
| $\min\left(\mu {\left\| {{\mathit{\boldsymbol{R}}_{\rm c}}} \right\|_*} + \frac{1}{2}\left\| {{P_\varOmega }({\mathit{\boldsymbol{R}}_{\rm c}}) - {\mathit{\boldsymbol{R}}_{\rm T}}} \right\|_2^2\right)$ | (17) |
式中:μ为常数;Rc为目标矩阵;
| $\begin{aligned}\\[-10pt] {P_\varOmega }({R_{\rm c}}(i,j)) = \left\{ \begin{array}{l}\!\!\!\!\!{R_{\rm T}}(i,j), i - j = {d_u};\\\!\!\!\!\! 0, \text{其他}\end{array} \right.\end{aligned}$ | (18) |
对于式(17)利用不动点延续算法[17]进行求解得到最优解。不动点延续算法原理可表示为:
| $\left\{ \begin{array}{l}\!\!\!\!\! {\mathit{\boldsymbol{Y}}^k} = \mathit{\boldsymbol{R}}_{\rm c}^k - \tau g(\mathit{\boldsymbol{R}}_{\rm c}^k),\\[8pt]\!\!\!\!\! \mathit{\boldsymbol{R}}_{\rm c}^{k + 1} = {\varGamma _{\tau \mu }}({\mathit{\boldsymbol{Y}}^k})\end{array} \right.$ | (19) |
式中,Rc的初始值取
| ${\varGamma _{\tau \mu }}(\mathit{\boldsymbol{Y}}) = {\mathit{\boldsymbol{U}}_{Y}}{\rm{diag(}}{s_{\tau \mu }}(\sigma ))\mathit{\boldsymbol{V}}_{Y}^*$ | (20) |
式中,
| ${s_{\tau \mu }}(\sigma ) = \tilde \sigma ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\tilde \sigma _i} = \left\{ \begin{array}{l}\!\!\!\!\! {\sigma _i} - \tau \mu ,{\rm{ }}{\sigma _i} - \tau \mu > 0;\\[5pt]\!\!\!\!\! 0,{\sigma _i} - \tau \mu \le 0\end{array} \right.$ | (21) |
通过式(19)求得式(17)的最优解Rc,进一步对Rc进行特征分解,即
| ${\mathit{\boldsymbol{R}}_{\rm c}} = {\mathit{\boldsymbol{U}}_{s}}{{\varSigma} _{s}}\mathit{\boldsymbol{U}}_{s}^{\rm H} + {\mathit{\boldsymbol{U}}_n}{{\varSigma} _n}\mathit{\boldsymbol{U}}_n^{\rm H}$ | (22) |
式中,
为了避免角度搜索的复杂性,令
| $f({\textit z}) = {{\textit z}^{2MN - N}}{\mathit{\boldsymbol{P}}^{\rm T}}({{\textit z}^{ - 1}}){\mathit{\boldsymbol{U}}_n}\mathit{\boldsymbol{U}}_n^{\rm H}\mathit{\boldsymbol{P}}({\textit z})$ | (23) |
求出式(23)中K个接近单位圆上的根
| ${\hat \theta _i} = {\rm arcsin}({\rm arg}({\hat {\textit{z}}_i})/{{\text{π} }})$ | (24) |
式中,
综上所述,FPC-root-MUSIC算法流程如下:
步骤1:对阵列接收数据进行时间平均以求采样协方差矩阵
步骤2:根据差联合阵列与波程差一一对应的关系,将
步骤3:利用FPC算法对
步骤4:对
步骤5:构造式(23)的求根多项式实现对DOA的估计。
3 仿真实验通过仿真实验对本文所提方法的性能进行分析,并与MUSIC方法、CO-Lasso方法以及文献[13–14]方法共5种方法进行比较。其中,MUSIC方法的角度搜索间隔为0.1°,CO-Lasso方法和文献[14]方法的完备字典间隔为0.1°。选用M=2,N=3,阵元数为6的互质阵列作为接收阵列,以均方根误差(root mean square errors, RMSE)作为衡量算法优劣的指标,角度均方根误差定义为:
| $RMS\!\!E(\theta ) = \frac{1}{K}\sum\limits_{j = 1}^K {\sqrt {\frac{1}{J}\sum\limits_{l = 1}^J {{{({{\hat \theta }_i} - {\theta _i})}^2}} } } $ | (25) |
式中,K为入射信号数,J为蒙特卡罗实验次数,
1)可行性分析
为了验证本文方法的可行性,假设9个等功率远场窄带信号入射到互质阵列上,入射角度分别为–70.12°、–50.34°、–30.02°、–10.25°、10.65°、30.46°、50.12°、60.24°、70.76°,信噪比SNR=10 dB,快拍数L=2 048。由于MUSIC方法此时已完全失效,这里没有给出仿真结果,其他4种方法的实验结果如图3所示。
 |
| 图3 4种方法的可估计信号数比较 Fig. 3 Comparison of resolvable signals number of the four methods |
由图3可知:本文方法利用6个阵元准确实现了对9个信号的DOA估计,而CO-Lasso方法可利用的阵列自由度为8均小于信号数,因此都无法对所有信号的DOA进行准确估计;文献[13]方法个别信号的DOA估计存在误差;文献[14]方法由于在稀疏重构过程中受到基不匹配的影响,对其中部分信号的DOA估计效果不佳。
2)分辨率比较
假设2个相近的等功率远场窄带信号入射到互质阵列上,入射角度分别为30.13°、32.26°,信噪比SNR=5 dB,快拍数L=500。将本文所提方法、CO-Lasso方法以及文献[13–14]方法的分辨率性能进行比较,图4为4种方法具体的分辨率结果。
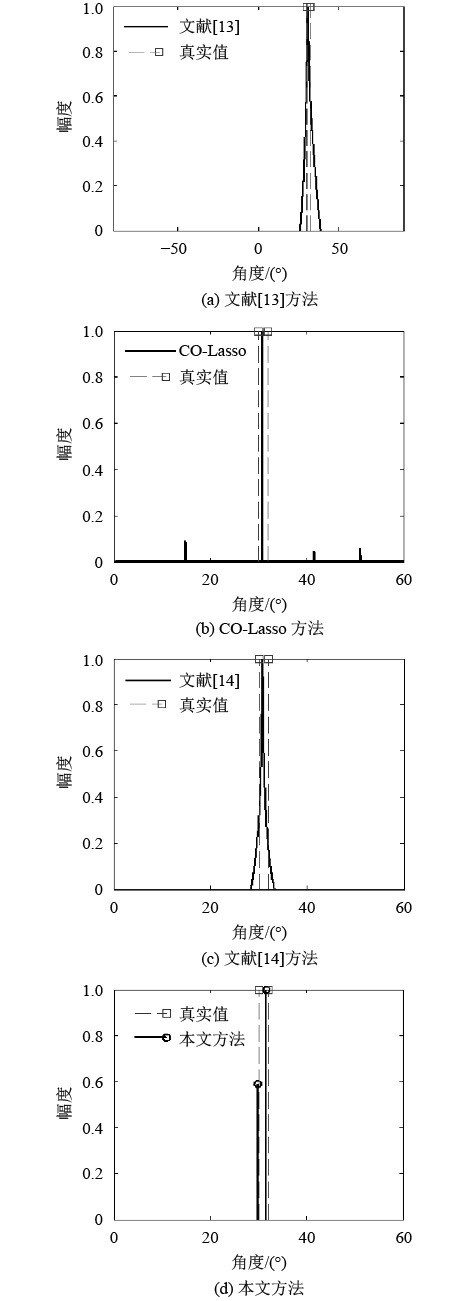 |
| 图4 4种方法的分辨率比较 Fig. 4 Comparison of the resolution of the four methods |
由图4可知,当两个信号的入射角度较近时,CO-Lasso方法和文献[13–14]方法均无法正确分辨,而本文方法依然具有良好的分辨率性能。因此,本文方法的分辨率性能要优于其他3种方法。
3)估计精度比较
假设2个等功率远场窄带信号入射到互质阵列上,入射角度分别为30.13°、60.25°,分析信噪比、快拍数对上述5种方法估计精度的影响,每个信噪比、快拍数下进行100次蒙特卡洛实验。图5为快拍数L=1 024,信噪比SNR从–5~15 dB,步长为5 dB时,角度均方根误差随信噪比变化关系;图6为信噪比SNR=10 dB,快拍数L为500~900,步长为100时,角度均方根误差随快拍数变化关系。
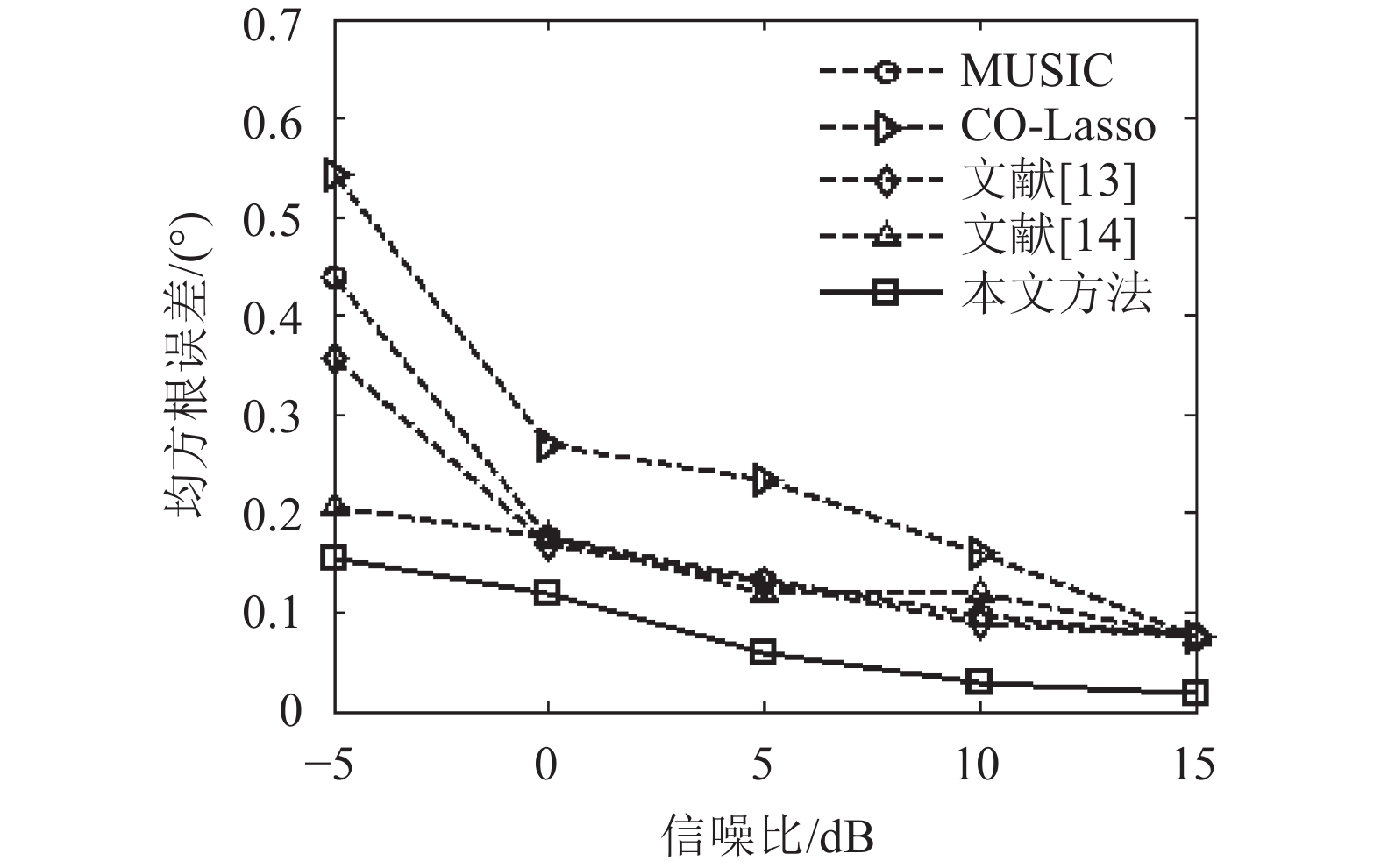 |
| 图5 角度均方根误差随信噪比变化 Fig. 5 RMSE with different SNR |
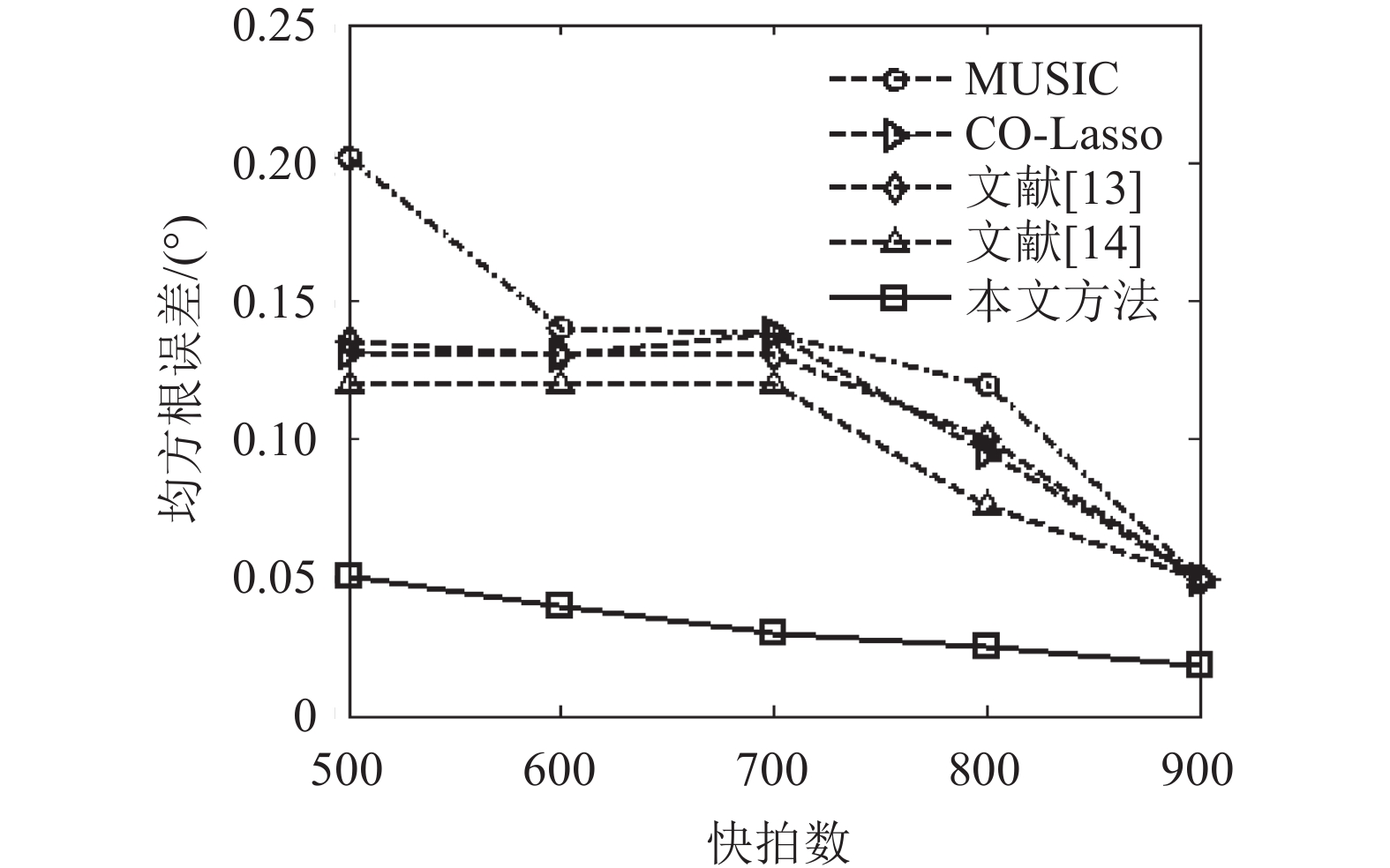 |
| 图6 角度均方根误差随快拍数变化 Fig. 6 RMSE with different snapshot number |
由图5、6的可知:在一定的信噪比、快拍数范围内,5种方法的角度均方根误差随着信噪比、快拍数的增加而减小。在相同的实验条件下,本文方法的估计精度要明显优于MUSIC方法、CO-Lasso方法以及文献[13–14]方法,尤其是在低信噪比、少快拍数情况下更明显。这是因为:一方面,本文方法对互质阵列的差联合阵列的空洞进行了有效填充,从而可利用的阵列自由度要高于其他4种方法。另一方面,MUSIC方法和文献[13]的估计精度受到角度搜索间隔的影响,CO-Lasso方法和文献[14]均在稀疏重构过程中受到基不匹配的影响,而本文方法有效避免这两种因素的影响。
4)分辨成功率比较
为了验证本文方法的分辨成功率与信噪比之间的关系,假设两个等功率远场窄带信号入射到互质阵列上,入射角度分别为30.13°、36.25°,实验所使用快拍数L=500。定义
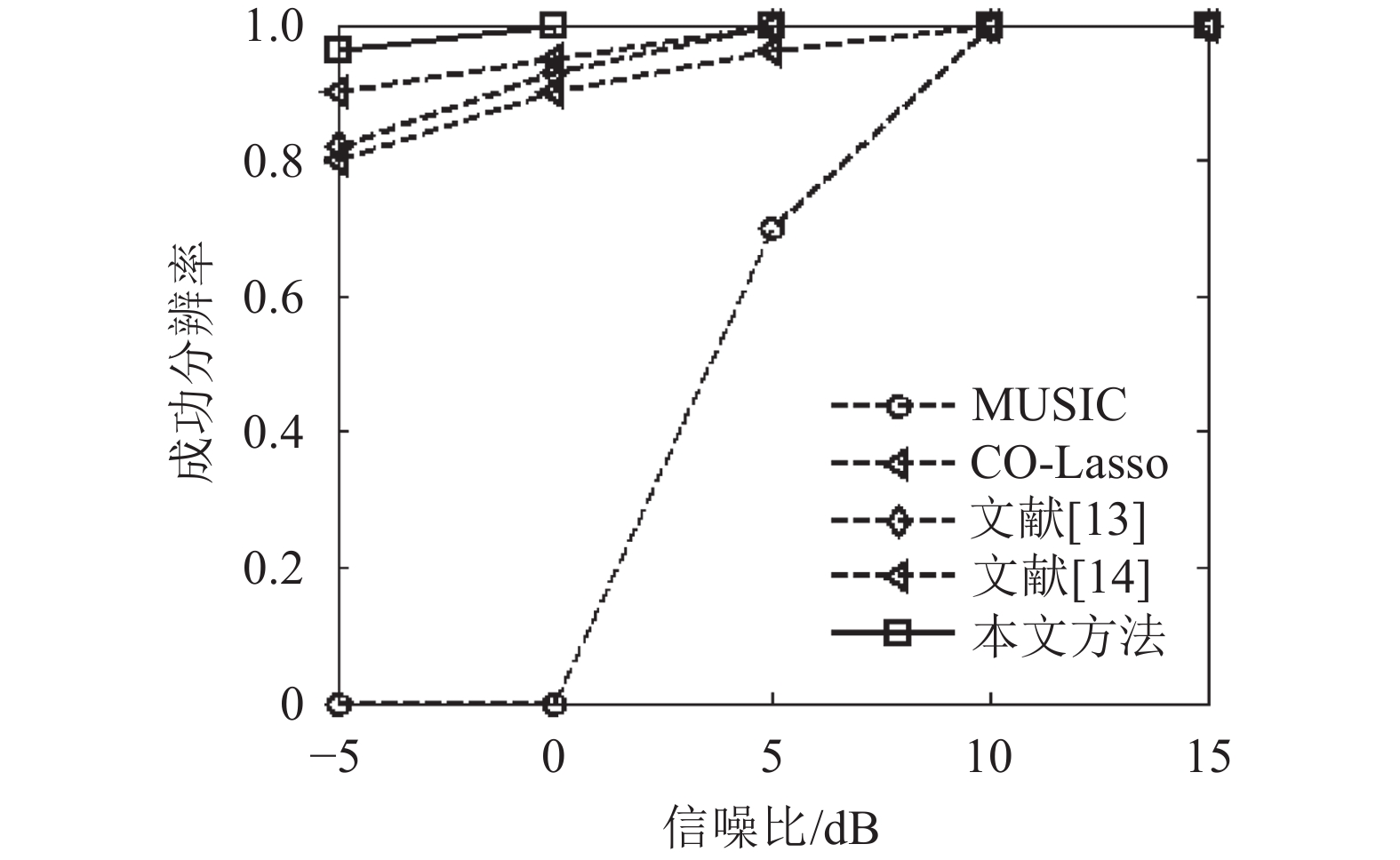 |
| 图7 4种方法的分辨成功率比较 Fig. 7 Success rates of resolution of four methods |
由图7可知:在一定的信噪比范围内,4种方法的成功分辨概率均随着信噪比的增加而增大。在–5~10 dB时,本文方法的分辨概率要明显高于MUSIC方法、CO-Lasso方法以及文献[13–14]方法。而当信噪比大于10 dB时,4种方法的分辨概率都达到100%。
5)时效性比较
实验条件与实验1)相同,将上述5种方法的运算时间进行比较。仿真环境为MATLAB 8.1平台,英特尔i7处理器,8 GB内存。分析信号数与运算时间之间的关系,具体实验结果如图8所示。
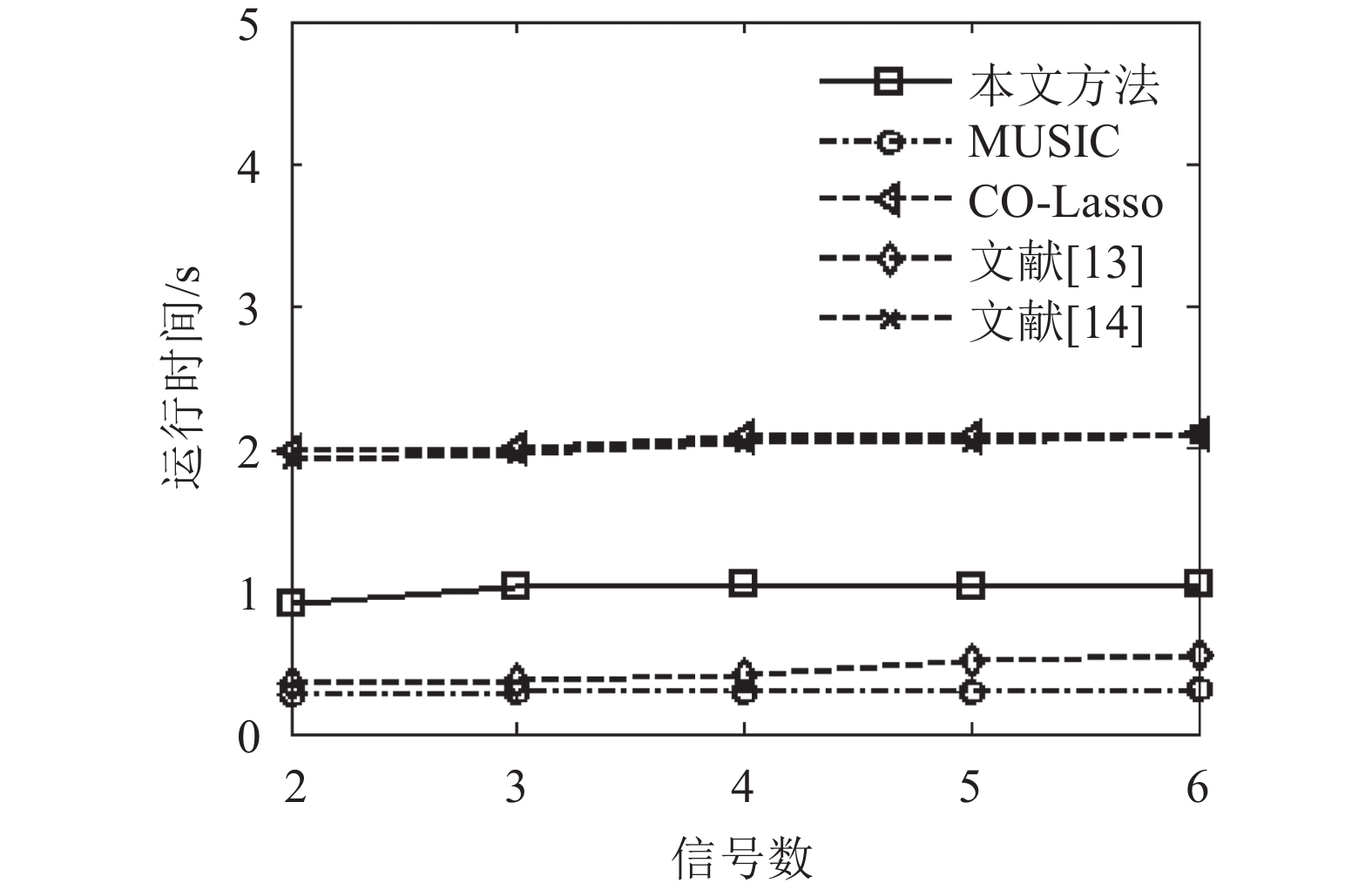 |
| 图8 运算时间随信号数变化 Fig. 8 Operation time variable with numbers of signal |
由图8可知,本文方法的计算时间明显少于CO-Lasso方法和文献[14]方法,但仍大于MUSIC方法和文献[13]方法,然而考虑到本文方法在估计精度和分辨率等方面的良好性能,这种运算性能的损失是可以接受的。
4 结 论研究了一种基于矩阵填充的互质阵列欠定DOA估计方法,该方法通过利用矩阵填充理论实现了对互质阵列的差联合阵列中空洞部分的有效填补,从而获得更高的阵列自由度。与现有方法相比,本文方法在提高可估计信号数的同时,能够有效避免传统稀疏重构算法中基不匹配对估计性能的影响,具有较高的估计精度和分辨率性能。下一步工作将针对如何矩阵填充理论应用于2维欠定DOA估计问题展开研究。
| [1] |
Vaidyanathan P P, Pal P. Sparse sensing with co-prime samplers and arrays[J]. IEEE Transaction on Signal Processing, 2011, 59(2): 573-586. DOI:10.1109/TSP.2010.2089682 |
| [2] |
Liu C L, Vaidyanathan P P. Remarks on the spatial smoothing step in coarray MUSIC[J]. IEEE Signal Processing Letters, 2015, 22(9): 1438-1442. DOI:10.1109/LSP.2015.2409153 |
| [3] |
Qin S, Zhang Y D, Amin M G. Generalized coprime array configurations for direction-of-arrival estimation[J]. IEEE Transaction on Signal Processing, 2015, 63(6): 1377-1390. DOI:10.1109/TSP.2015.2393838 |
| [4] |
Zhang Y D,Qin S,Amin M G.DOA estimation exploiting coprime arrays with sparse sensor spacing[C]//Acoustics,Speech and Signal Processing (ICASSP).Heidelberg:IEEE,2014:2267–2271.
|
| [5] |
Pal P, Vaidyanathan P P. Pushing the limits of sparse support recovery using correlation information[J]. IEEE Transaction on Signal Processing, 2015, 63(3): 711-726. DOI:10.1109/TSP.2014.2385033 |
| [6] |
Shen Q, Liu W, Cui W. Low-complexity direction-of-arrival estimation based on wideband co-prime arrays[J]. IEEE/ACM Transaction on Audio,Speech,and Language Processing, 2015, 23(9): 1445-1456. DOI:10.1109/TASLP.2015.2436214 |
| [7] |
Wanghan L V, Huali W, Feng L I U. Wideband DOA estimation based on co-prime arrays with sub-Nyquist sampling[J]. IEICE Transactions on Fundamentals of Electronics,Communications and Computer Sciences, 2016, 99(9): 1717-1720. |
| [8] |
Shen Q, Cui W, Liu W. Underdetermined wideband DOA estimation of off-grid sources employing the difference co-array concept[J]. Signal Processing, 2017, 130(3): 299-304. |
| [9] |
Shen Q, Liu W, Cui W. Extension of co-prime arrays based on the fourth-order difference co-array concept[J]. IEEE Signal Processing Letters, 2016, 23(5): 615-619. DOI:10.1109/LSP.2016.2539324 |
| [10] |
Chi Y, Scharf L L, Pezeshki A. Sensitivity to basis mismatch in compressed sensing[J]. IEEE Transaction on Signal Processing, 2011, 59(5): 2182-2195. DOI:10.1109/TSP.2011.2112650 |
| [11] |
Tan Z, Nehorai A. Sparse direction of arrival estimation using co-prime arrays with off-grid targets[J]. IEEE Signal Processing Letter, 2014, 21(1): 26-29. DOI:10.1109/LSP.2013.2289740 |
| [12] |
Ramirez J,Krolik J.Multiple source localization with moving co-prime arrays[C]//Proceedings of the 2015 IEEE International Conference on Acoustics,Speech and Signal Processing (ICASSP).Porland:IEEE,2015:2374–2378.
|
| [13] |
BouDaher E, Jia Y, Ahmad F. Multi-frequency co-prime arrays for high-resolution direction-of-arrival estimation[J]. IEEE Transaction on Signal Processing, 2015, 63(14): 3797-3808. DOI:10.1109/TSP.2015.2432734 |
| [14] |
BouDaher E,Ahmad F,Amin M G.Sparsity-based extrapolation for direction-of-arrival estimation using co-prime arrays[C]//SPIE Commercial Scientific Sensing and Imaging.International Society for Optics and Photonics.Colorado:IEEE,2016:98570L-98570L-6.
|
| [15] |
Candes E J, Recht B. Exact matrix completion via convex optimation[J]. Foundations of Computational Mathematics, 2009, 9(6): 717-772. DOI:10.1007/s10208-009-9045-5 |
| [16] |
Cai J F, Candes E J, Shen Z. A singular value thresholding algorithm for matrix completion[J]. SIAM Journal on Optimization, 2010, 20(4): 1956-1982. DOI:10.1137/080738970 |
| [17] |
Chen C, He B, Yuan X. Matrix completion via an alternating direction method[J]. IMA Journal of Numerical Analysis, 2012, 32(1): 227-245. DOI:10.1093/imanum/drq039 |
| [18] |
Kalogerias D S, Petropulu A P. Matrix completion in collocated MIMO radar:Recoverability,bounds & theoretical guarantees[J]. IEEE Transaction on Signal Processing, 2014, 62(2): 309-321. DOI:10.1109/TSP.2013.2287673 |
| [19] |
Li B,Petropulu A.Spectrum sharing between matrix completions based MIMO radars and a MIMO communication system[C]//Acoustics,Speech and Signal Processing (ICASSP).New Zealand:IEEE:2015:2444–2448.
|
| [20] |
Ma S, Goldfarb D, Chen L. Fixed point and Bregman iterative methods for matrix rank minimization[J]. Mathematical Programming, 2011, 128(1/2): 321-353. |
| [21] |
Hu Y, Zhang D, Ye J. Fast and accurate matrix completion via truncated nuclear norm regularization[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 2013, 35(9): 2117-2130. DOI:10.1109/TPAMI.2012.271 |
| [22] |
Recht B. A Simpler approach to matrix completion[J]. Journal of Machine Learning Research, 2011, 12(4): 3413-3430. |
 2017, Vol. 49
2017, Vol. 49

