2. 中国科学院 水利部 成都山地灾害与环境研究所,四川 成都 610041;
3. 中国科学院大学,北京 100049;
4. 中国科学院 青藏高原地球科学卓越创新中心,北京 100101
2. Inst. of Mountain Hazards and Environment,CAS,Chengdu 610041,China;
3. Univ. of Chinese Academy of Sciences,Beijing 100049,China;
4. CAS Center for Excellence in Tibetan Plateau Earth Sciences,Beijing 100101,China
倾倒破坏是反倾向层状岩体边坡常见的一种破坏模式,在自然和工程边坡中均有发生[1–2]。按破坏机制的不同,Goodman等[3]将倾倒破坏模式分为两类:弯曲倾倒和块体倾倒(块体–弯曲倾倒为两者的复合形式)。块体倾倒破坏机制简单,破坏面为确定的直线或者双折线,国内外学者在该方面的研究已取得显著成果,并建立较为完善的理论分析方法[4–7]:Aydan等[4]得出块体边坡在倾斜面上的倾倒破坏条件;Bobet[5]从连续介质的角度推导了块体间作用力的表达式;Liu等[6]提出岩质边坡块体倾倒破坏的传递系数法;Yagoda等[7]推导了斜面上单个块体在地震作用下的倾倒破坏条件。弯曲倾倒破坏相对较为复杂,由于反倾向边坡破坏面的位置、形状和破坏岩层的个数未知,使得学者难以从理论上定量分析岩层间的力学作用机制。从19世纪60年代到80年代,近20年时间,研究者往往只是通过物理现象描述弯曲倾倒破坏问题[8–9],并不能从根本上阐述弯曲倾倒破坏的力学机理,弯曲倾倒破坏的理论研究远远滞后于工程实际。
为确定反倾向层状边坡弯曲倾倒破坏面的位置和形状,专家学者开展了大量物理模型试验。1992年,Aydan等[10]通过基底摩擦试验最先研究了弯曲倾倒边坡,并得出破坏面是一条通过坡脚的直线(也称作破坏基准线),垂直于岩层层面;认为破坏基准线所延伸到的岩层都发生了破坏,并且岩层只发生弯曲拉裂破坏。随后,Adhikary等[11]通过离心机模型试验对Aydan等的研究理论进行完善,发现破坏面与岩层垂直面之间有一定的夹角,约为10°。2009年,Aydan等[12]基于模型试验考虑了地震作用下岩层的弯曲倾倒破坏特征,并得出破坏面与岩层法平面的夹角为0°~15°。
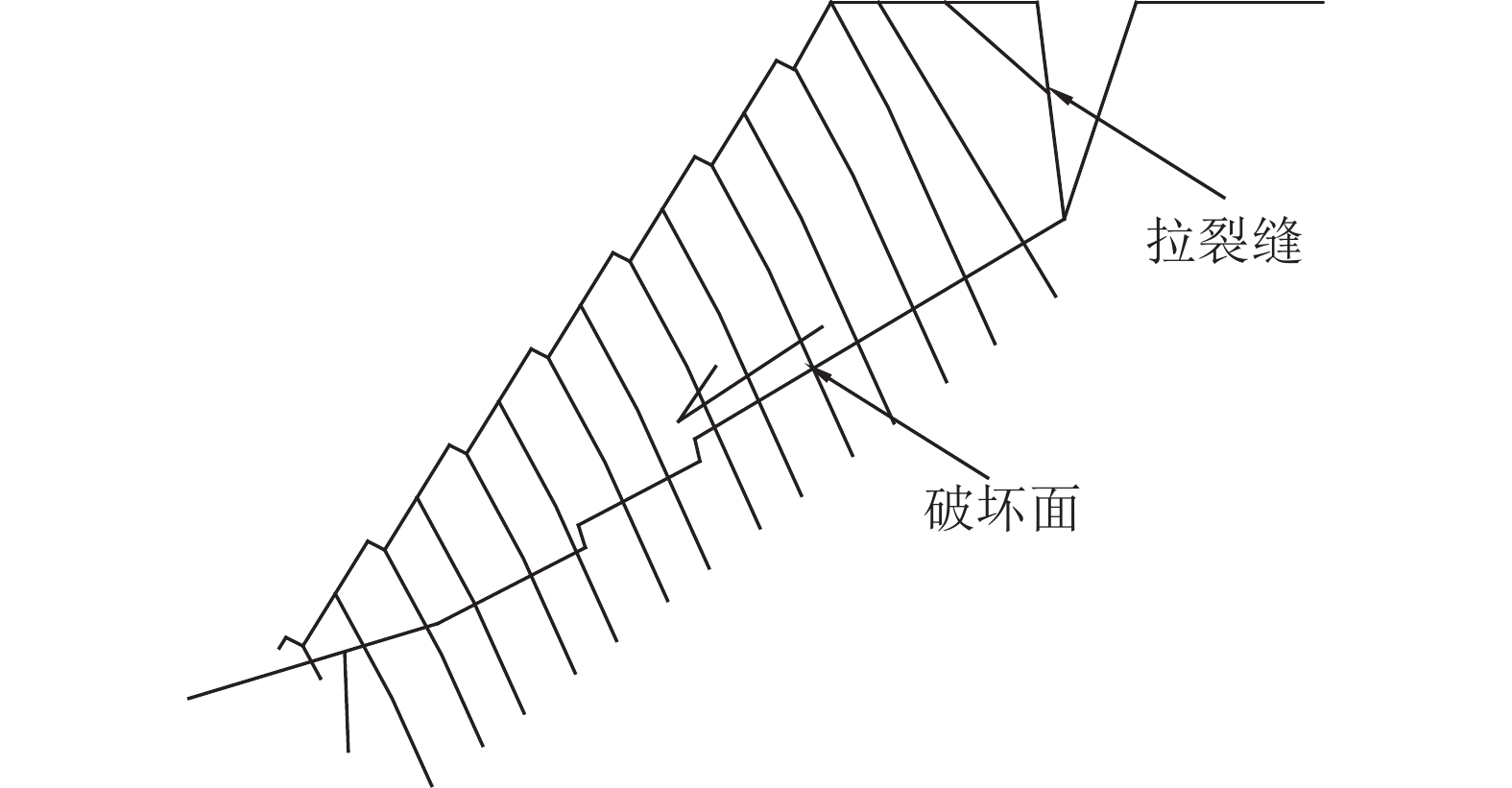
通过物理模型试验得出的破坏基准面,极大推动了弯曲倾倒破坏理论研究的发展,然而从野外观测和工程实际[13–14]来看,大量反倾向层状边坡弯曲倾倒破坏面并非直线型(图1),这种现象在板岩边坡中[14]尤为明显。此外,岩层的破坏也不只是弯曲拉裂所致,边坡坡脚附近常伴有剪出口[13]。于是,许多学者结合野外实际调查,进一步修正了反倾向层状边坡弯曲倾倒破坏面的形式、位置,完善了反倾向层状边坡的破坏模式。这些改进主要关注两方面内容:一方面是单个岩层的折断位置和判据,另一方面是岩层整体破坏位置和形式。
 |
| 图1 某反倾向层状边坡破坏面 Fig. 1 One countertendency layered toppling slope |
伍法权[15]以库仑强度理论为依据,对薄片状云母石英片岩斜坡弯曲倾倒变形做了若干分析,得出主应力与层间内摩擦角关系的判据;但这种关系判据只适用于不计自重与刚度的极薄片层状岩体。陈红旗等[16]基于最大拉应力准则,提出岩层弯曲折断的应力判据和挠度判据,并给出岩层极限高度的算法。蒋良潍等[17]建立等厚弹性悬臂板梁模型,推导出弹性屈曲临界条件和弯折临界条件。上述研究为单个岩层折断位置的确定提供了理论依据。
卢海峰等[18]结合边坡实际破坏过程,对Aydan和Kawamoto的悬臂梁模型进行了优化,认为破坏面为Adhikary断裂面和岩层自重断裂面组合而成;但卢海峰等得出的临界失稳长度只是在自重作用下的情形,并未考虑层间作用力的影响。蔡静森等[13]通过野外观测和力学分析,得出岩层的破坏是弯曲拉裂和压缩剪切共同作用的结果,运用新提出的基准面理论对岩层变形几何空间条件进行分区,然后讨论岩层分区破坏模式的力学机制,并确定每个岩层的断裂深度,最后确定整个反倾向层状边坡的破坏面。陈从新等[19]通过对模型试验结果的分析,阐明岩质反倾边坡弯曲倾倒的破坏过程和破坏机制,并认为破坏面为一折线,叠合倾倒区和悬臂倾倒区的分界点以下为直线,分界点以上为台阶型。
以上研究进一步完善了反倾向层状边坡弯曲倾倒破坏的理论基础,但上述研究至少存在以下问题中的一个:1)忽略了层间力的作用;2)缺乏严格的力学推导;3)忽略了节理裂隙对岩质边坡稳定性的影响;4)无法准确确定岩层破坏数目。为解决上述问题,本文提出一种搜索弯曲倾倒破坏基准面的计算方法。该方法采用悬臂梁模型,以潘家铮极值原理[20–21]和极限平衡理论为理论依据,结合严格的力学推导确定岩层的破坏模型和破坏数目,弥补了现有半理论半经验方法的不确定性,提高了弯曲倾倒理论分析的可靠性。
1 地质几何模型反倾向层状边坡如图2所示:H为边坡高度;β为边坡倾角;η为岩层倾角;θ0为自然坡角;α为岩层法向倾角;θ为岩层i破裂面倾角;θr为岩层i的破裂面倾角与其法向倾角的夹角;β0为边坡倾角与岩层法向倾角之差;b为岩层厚度;hi为岩层i与岩层i+1的接触长度;εi为岩层i底部不连通率,
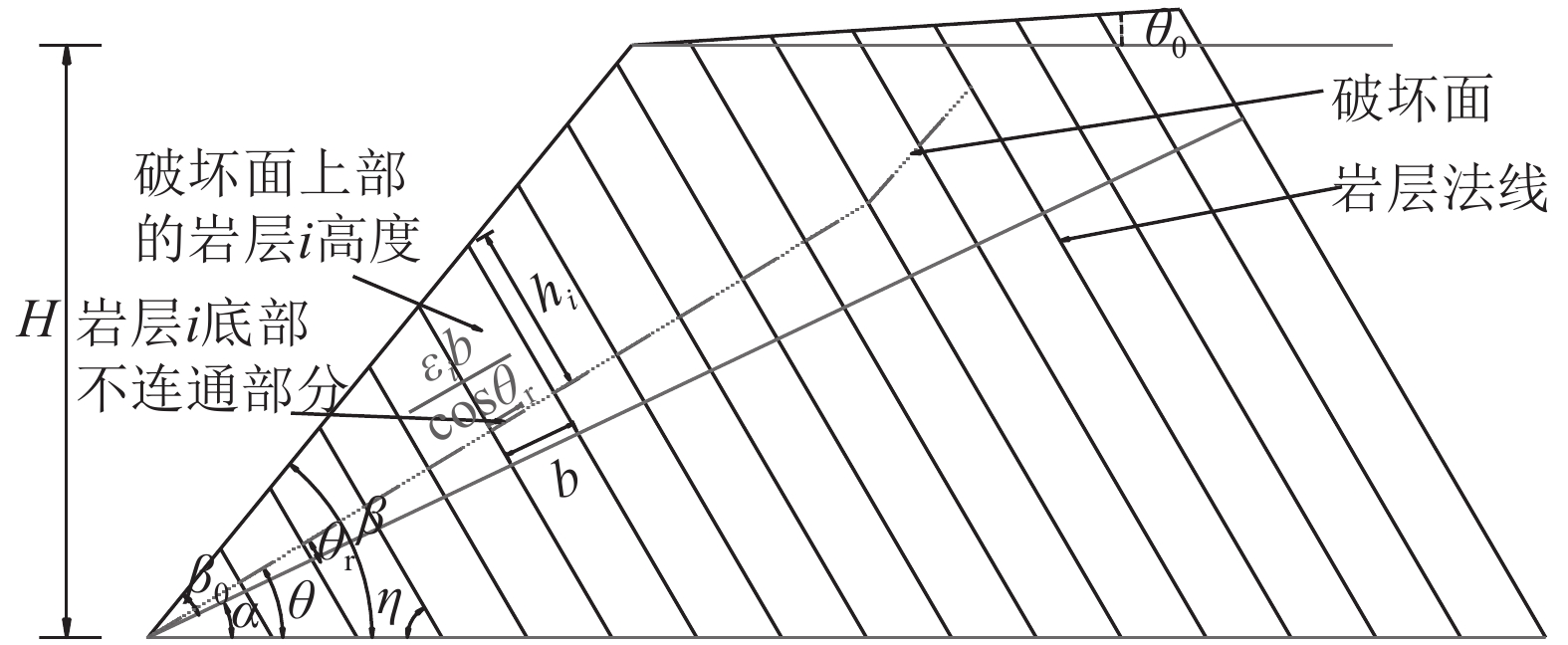 |
| 图2 反倾向层状边坡地质几何模型 Fig. 2 Geological geometric model of countertendency layered slope |
| $\left\{ \begin{aligned}& \alpha = \text{π} /2 - \eta, \\& {\beta _0} = \beta - \alpha, \\& \theta = \alpha + {\theta _{\rm r}}\end{aligned}\right.$ | (1) |
根据工程经验和文献资料[22–23]可知,岩质边坡的最终破坏大多是岩体节理贯通所致。由于岩体节理裂隙空间分布复杂,现有手段难以建立合适的物理模型,当前的弯曲倾倒理论研究中鲜有涉及到对节理裂隙的考虑。为解决这一难题,本文对含节理裂隙的边坡做一种等效弱化,假定每块岩层的潜在破坏面底部都存在节理裂隙,节理裂隙都集中在岩层底面右侧,左侧为未连通部分,节理裂隙方向始终与破坏面保持一致。基于已有弯曲倾倒破坏研究的分析结论,采用以下几条假设简化弯曲倾倒破坏的分析过程:
1)各个岩层的厚度相等;
2)在临界破坏状态,所有岩层沿边坡潜在破坏面处于极限平衡状态;
3)以岩层为基本单元,将岩层面上的力简化为集中力,作用点位于χhi处;
4)每个岩层的破坏面由岩层底部节理裂隙贯通形成。
3 搜索破坏面 3.1 基本思想根据潘家铮最大最小原理[20–21]可知:边坡发生整体破坏时必定沿着抵抗力最小的破坏面(如果存在)滑动(极小值原理),同时边坡会在此破坏面上自行调整应力状态,以发挥最大抗滑力(极大值原理)。因此可以推断:反倾向层状边坡的潜在最危险破坏面必定是抵抗力最小的破坏面,此时边坡发生整体破坏所需外力F达到最小值。若F大于0,则边坡处于稳定状态;若F等于0,则边坡处于极限状态;若F小于0,则边坡不稳定。
根据野外实际观测[13–14]、试验研究[24–25]和理论分析[22–23],假定发生弯曲拉裂破坏的所有岩层的破裂面是平行于岩层法向方向的一条直线,且岩层发生破裂的位置由岩层的应力状态决定;发生剪切破坏的各个岩层的破裂面是与岩层法向方向成一定角度的一条直线,角度的大小由剪切破坏区各个岩层的应力状态共同决定;将单个岩层折断面的中点相互连接,即为最终所求得的破坏基准面。于是,边坡的破坏面即为一个关于岩层折断高度hi和剪切破坏角θr的函数,其中边坡发生整体破坏所需外力最小的破坏面即为边坡最可能失稳的破坏面。那么,上述问题就变成了一个最优化问题,即
| $\left\{ \begin{aligned}& F = \min ({T_{nn}}({h_i},{\theta _{\rm r}})),\;\; 1 \le nn \le n; \\& {T_i}({h_i},{\theta _{\rm r}}) = \left\{\!\!\!\! \begin{array}{l}{P_i}({h_i},{\theta _{\rm r}}),\;\; 1 \le i \le nst;\\{T_i}({h_i},{\theta _{\rm r}}),\;\; nst < i \le nn;\end{array} \right.\\& 0 \le {\theta _{\rm r}} \le {\beta _0}\end{aligned}\right.$ | (2) |
其中,nst为最后一块发生剪切破坏的岩层编号,nn为可能破坏的岩层个数,n为岩层总数,β0为边坡倾角与岩层法向倾角的差值。搜索角的大小可以通过如下方式确定:
| ${\theta _{\rm r}} = j\Delta {\theta _{\rm r}},\ 0 \le j \le nm$ | (3) |
| $\Delta {\theta _{\rm r}} = {\beta _0}/nm$ | (4) |
式中:∆θr是搜索步长;nm为搜索次数,取为106。
3.2 确定岩层破坏模式对于反倾向层状边坡,弯曲倾倒破坏为主要破坏模式,其实质是岩层由于弯曲引起的拉应力超过了岩柱的最大抗拉强度,即发生弯曲拉裂破坏。但根据野外观测[13–14]和模型试验[24–25]可知,坡体内部某些岩层可能发生剪切破坏;且通过理论分析可知[22–23],这种情况是可能存在的:当岩层长细比很小时,岩层具有较强的抗倾倒能力,此时岩层发生弯曲倾倒破坏的机率较小,在自重和上部岩层的推力作用下,坡脚岩层发生剪切破坏的可能性较大。鉴于此,将边坡破坏区分为坡脚剪切破坏区和中上部弯曲拉裂破坏区,哪种破坏条件先满足,岩层便以该破坏模式发生破坏。
如图3所示,若岩层i发生剪切破坏,则必定满足摩尔–库仑准则,即
| $\tau = \sigma \tan\, {\textit φ} + c$ | (5) |
式中,τ为剪应力,σ为正应力,φ为内摩擦角,c为黏聚力。
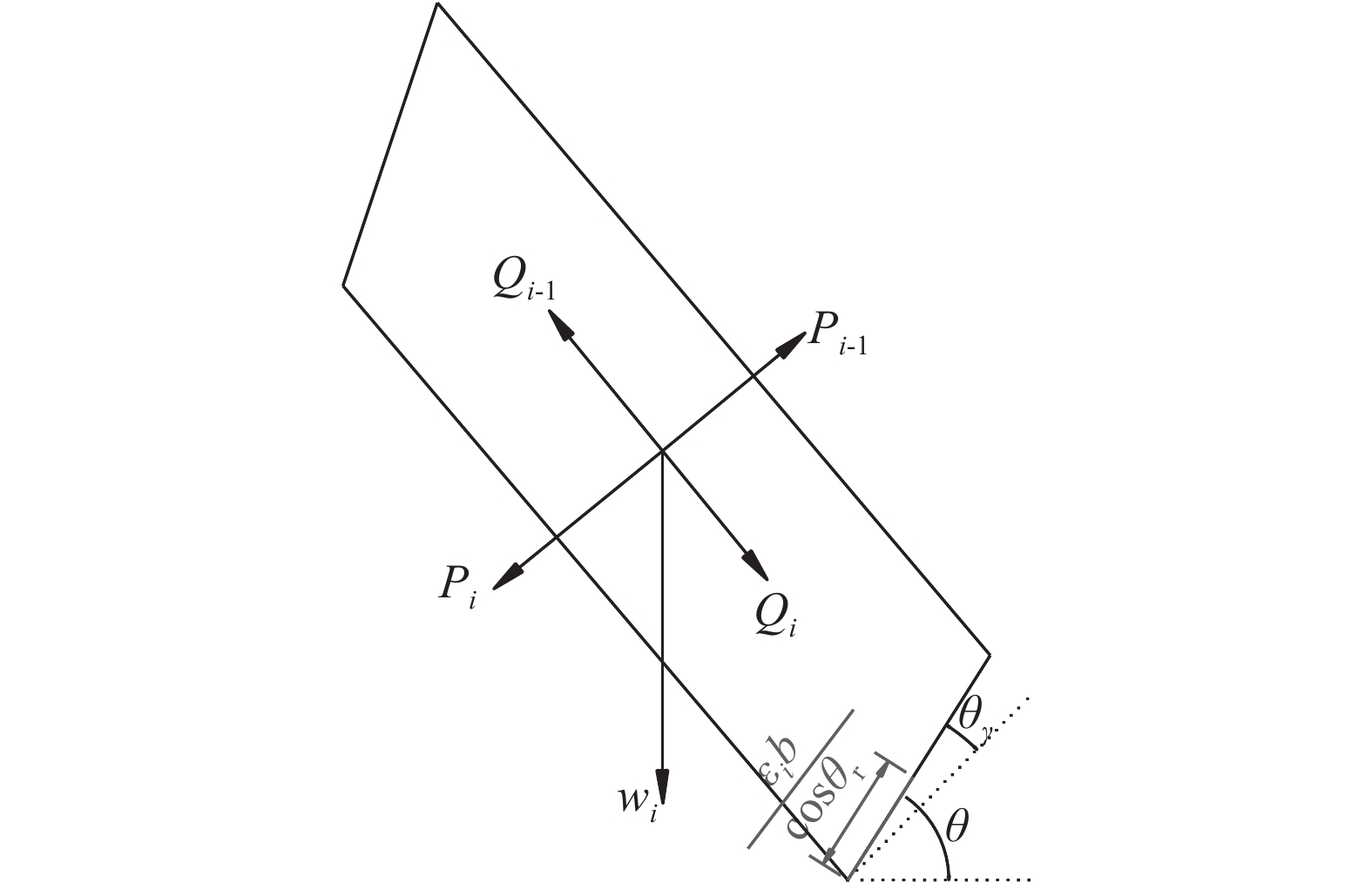 |
| 图3 岩层i发生剪切破坏的受力分析 Fig. 3 Force analysis chart of stratum i occurred shear failure |
将式(5)左右两端同时乘以岩层底面未贯通部分的长度
| ${\varepsilon _i}\tau b/\cos \ {\theta _{\rm{r}}} = {\varepsilon _i}b\sigma \tan \ {\textit φ} /\cos \ {\theta _{\rm{r}}} + {\varepsilon _i}cb/\cos \ {\theta _{\rm{r}}}$ | (6) |
即
| ${\varepsilon _i}{S_i} = {\varepsilon _i}{N_i}\tan \ {\textit φ} + {\varepsilon _i}cb/\cos \ {\theta _{\rm{r}}}$ | (7) |
其中,Si、Ni分别为岩层i底面的切向力和法向力。
对于岩层底面贯通的部分,岩层滑动时应满足库仑摩擦定律,即
| $\tau = \sigma \tan \ {\textit φ}$ | (8) |
将式(8)的左右两端同时乘以贯通部分的长度
| $(1 - {\varepsilon _i})b\tau /\cos \ {\theta _{\rm{r}}} = (1 - {\varepsilon _i})b\sigma \tan\ {\textit φ} /\cos\ {\theta _{\rm{r}}}$ | (9) |
即
| $(1 - {\varepsilon _i})S_i = (1 - {\varepsilon _i})N_i \tan \ {\textit φ}$ | (10) |
将式(7)与(10)相加即可得:
| ${S_i} = {N_i}\tan \ {\textit φ} + {\varepsilon _i}cb$ | (11) |
将岩层i所承受的力沿岩层底面切向和法向进行分解,则其底面的切向力和法向力分别为:
| $\begin{aligned}[b]{S_i} = & {w_i}\sin \ \theta + {Q_i}\sin \ {\theta _{\rm{r}}} + {P_i}\cos \ {\theta _{\rm{r}}} - {Q_{i - 1}}\sin \ {\theta _{\rm{r}}} - \\& {P_{i - 1}}\cos \ {\theta _{\rm{r}}}\end{aligned}$ | (12) |
| $\begin{aligned}[b]{N_i} = & {w_i}\cos \ \theta + {Q_i}\cos \ {\theta _{\rm{r}}} - {P_i}\sin \ {\theta _{\rm{r}}} - {Q_{i - 1}}\cos \ {\theta _{\rm{r}}} + \\& {P_{i - 1}}\sin \ {\theta _{\rm{r}}}\end{aligned}\!\!\!\!\!$ | (13) |
且满足:
| ${Q_i} = {P_i}\tan \ {{\textit φ} _i}$ | (14) |
| ${Q_{i - 1}} = {P_{i - 1}}\tan \ {{\textit φ} _i}$ | (15) |
| ${w_i} = {{ \overline h_i}} b\gamma $ | (16) |
式中,wi为岩层i位于破坏面上部的岩体重力,
联立式(5)~(16),可得:
| $\begin{aligned}[b]\!\!\!\!\! {P_i} \!=\! & {P_{i - 1}} \!+\! (\cos \ \theta (\tan \ {\textit φ} \!-\! \tan \ \theta ){w_i} \!+\! {\varepsilon _i}cb/\cos \ {\theta _{\rm{r}}})/(\cos \ {\theta _{\rm{r}}} \cdot \\& (1 + \tan \ {{\textit φ} _i}\tan \ {\theta _{\rm{r}}}) + \tan \ {\textit φ} \cos \ {\theta _{\rm{r}}}(\tan \ {\theta _{\rm{r}}} - \tan \ {{\textit φ} _i}))\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\end{aligned}$ | (17) |
若岩层i发生弯曲拉裂破坏,则必定满足最大拉应力理论,即
| ${\sigma _{\max }} = {\sigma _{\rm t}}$ | (18) |
| ${\sigma _{\max }} = \frac{{6{M_i}}}{{{\varepsilon ^2}{b^2}}} - \frac{{{N_i}}}{{\varepsilon b}}$ | (19) |
式中,Mi为岩层i底面未贯通部分中心的弯矩,Ni为岩层i的轴力。
如图4所示,岩层i底面未贯通部分中心的倾倒力矩和轴力分别为:
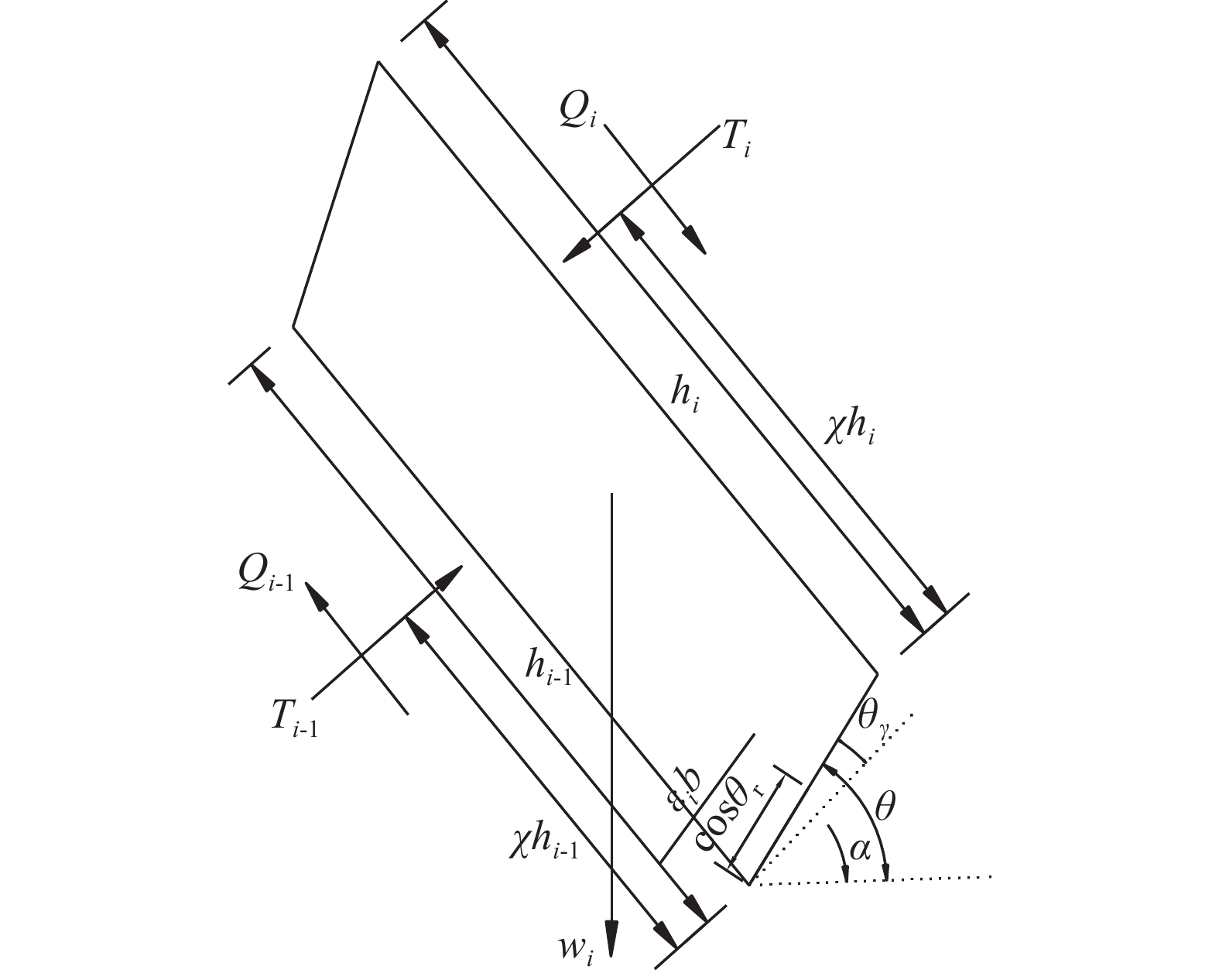 |
| 图4 岩层i发生弯曲拉裂破坏的受力分析 Fig. 4 Force analysis chart of stratum i occurred shear failure |
| $\begin{aligned}[b]& {M_i} = \frac{{ {{\overline h_i}} }}{2}{w_i}\sin \ \alpha + {T_i}\chi {h_i} - {Q_i}b(1 - \frac{\varepsilon }{2}) - {T_{i - 1}}\chi {h_{i - 1}}-\\ & \quad\quad {Q_{i - 1}}\frac{{b\varepsilon }}{2} - {w_i}\cos \ \alpha \frac{{b(1 - \varepsilon )}}{2}\end{aligned}\!\!\!\!\!\!\!\!$ | (20) |
| ${N_i} = {w_i}\cos \ \alpha $ | (21) |
且满足:
| ${Q_i} = {T_i}\tan \ {{\textit φ} _i}$ | (22) |
| ${Q_{i - 1}} = {T_{i - 1}}\tan \ {{\textit φ} _i}$ | (23) |
| $\chi \in [0,1]$ | (24) |
其中:Ti为岩层i受到上部岩层的法向推力;Ti–1为岩层i受到下部岩层的法向推力;hi–1为岩层i与岩层i–1的接触长度;χ为推力线高度,Adyan取0.5,Adhikary建议取0.6,本文取0.6。
联立式(18)~(24),可得:
| $\begin{aligned}[b]{T_i} = & \frac{1}{{\chi {h_i} - b(1 - \displaystyle\frac{\varepsilon }{2})\tan \ {{\textit φ} _i}}}[{T_{i - 1}}(\chi {h_{i - 1}} + \frac{1}{2}b\varepsilon \tan \ {{\textit φ} _i}) + \\& (\frac{{{\varepsilon ^2}{b^2}{\sigma _{\rm t}}}}{6} + \frac{{b{w_i}\cos \ \alpha (3 - 2\varepsilon )}}{6}) - \frac{{ {{\overline h_i}} }}{2}{w_i}\sin \ \alpha ]\end{aligned}\!\!\!\!\!\!\!\!\!\!\!\!\!\!$ | (25) |
对岩层i而言,若Pi≤Ti,即岩层i发生剪切破坏所需的推力小于发生弯曲拉裂破坏所需的推力,此时岩层i更容易发生剪切破坏;反之,若Ti<Pi,岩层i更容易发生弯曲拉裂破坏。那么,坡脚区发生剪切破坏的破坏区域判断准则为:
| $\left\{ \begin{aligned}& {P_i} \le {T_i},\\& {P_{i + 1}} > {T_{i + 1}} \end{aligned}\right.$ | (26) |
在破裂面的搜索过程中,发生破坏的岩层数目nn是未知的,这将给搜索带来极大困难。为使每步搜索更有目的性,必须确定当前搜索角θr下的最优岩层破坏个数,以往的观点认为基准线所延伸的岩层都发生了破坏[10–12],显然这种看法并不合理。借助最优化的思想,本文认为每个搜索角θr下边坡发生整体破坏所需外力最小的岩层组合,即为最危险的岩层组合。
如图5所示,岩层在自重作用下,发生弯曲折断破坏的极限高度为:
| ${h_0} = \frac{{{\varepsilon _i}(b\cos \ \alpha + \sqrt {{b^2}{{\cos }^2}\alpha + 12b{\sigma _{\rm{t}}}\sin \ \alpha /\gamma } )}}{{6\sin \ \alpha }}$ | (27) |
破坏面上部岩层i高度hi的表达式为:
| $ {h_i}=\left\{\begin{aligned}& ib(\tan \ {\beta _0} - \tan \ {\theta _{\rm r}}), \ 1 \le i < ntp; \\[5pt]& ib(\tan \ {\beta _0} - \tan \ {\theta _{\rm r}}) - (ib - (H/\sin \ \beta )\cos \ {\beta _0}) \cdot \\[5pt]& \quad\quad (\tan \ {\beta _0} + \cot \ {\beta _1}), \ i \ge ntp\end{aligned}\!\!\!\!\!\!\!\!\right. $ | (28) |
式中,
破坏面上部的岩层i等效高度
| $ {{\overline h_i}}= \left\{\begin{aligned}& (i + i - 1)b(\tan \ {\beta _0} - \tan \ {\theta _{\rm r}})/2, \; 1 \le i < ntp;\\& [(i + i - 1)b(\tan \ {\beta _0} - \tan \ {\theta _{\rm r}}) - (ib - (H/\sin \ \beta ) \cdot \\& \cos \ {\beta _0})(\tan \ {\beta _0} + \cot \ {\beta _1})]/2,\; i = ntp;\\& [(i + i - 1)b(\tan \ {\beta _0} - \tan \ {\theta _{\rm r}}) - ((i + i - 1)b-\\ & 2(H/\sin \ \beta )\cos \ {\beta _0}) (\tan \ {\beta _0} + \cot \ {\beta _1})]/2, \;\; i > ntp\end{aligned}\right.$ | (29) |
对最后一块破坏的岩层而言,由于不受到上部岩层的作用力,而下部岩层仅提供抵抗力,所以岩层发生弯曲折断破坏只可能是岩层重力所导致的(只考虑岩层自重力和层间相互作用力),那么其位于破坏面上部的等效高度
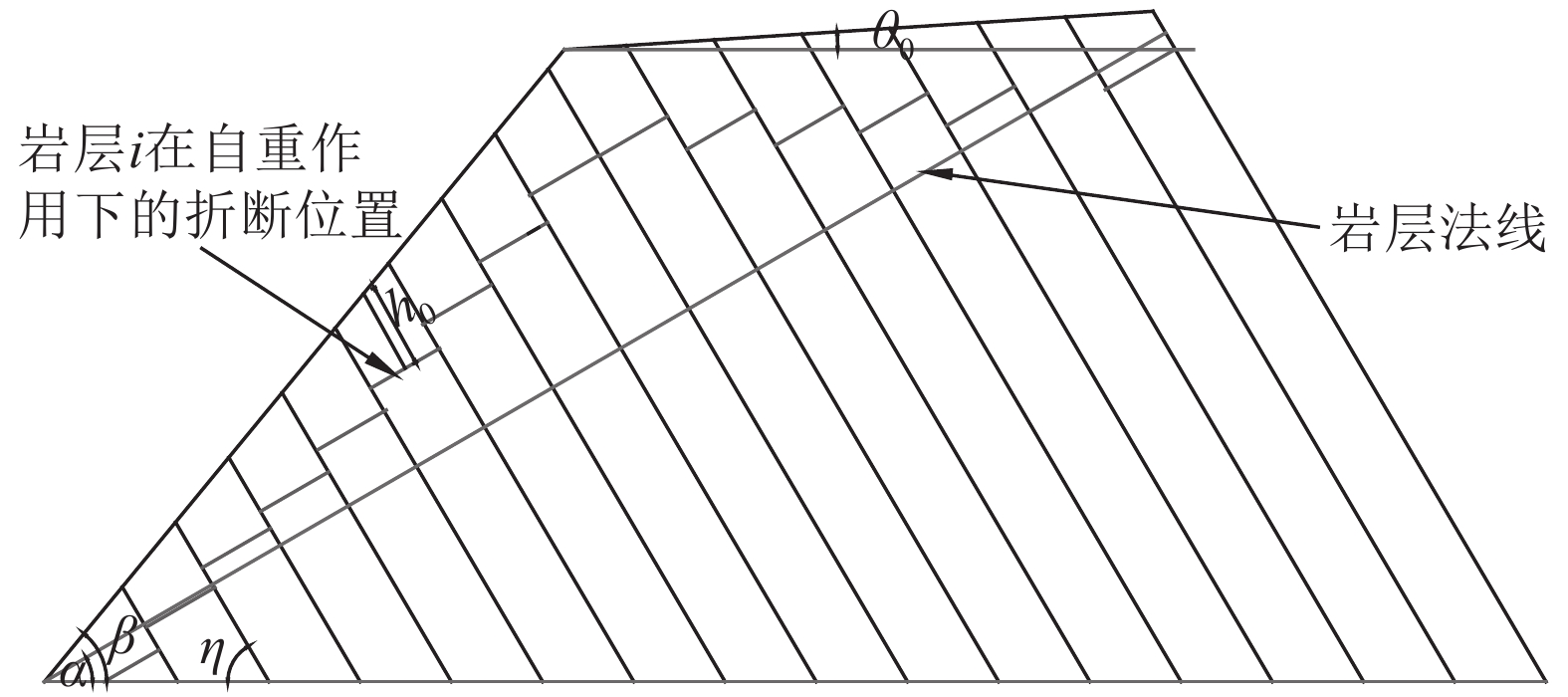 |
| 图5 各岩层在自重作用下的折断位置 Fig. 5 Breaking position of each rock stratum under the self-gravity |
根据式(28)可得到位于破坏面上部的岩层高度hi,再通过逐步迭代的方式计算岩层发生整体破坏所需外力F。不断变换岩层组合,会得到一系列外力F,其中的最小值作为边坡发生整体破坏所需最小外力,对应的岩层组合为最危险的岩层组合。
在搜索过程中,若出现Tnn<0(n_startd≤nn≤n_end),即岩层1~nn不需要外力就能破坏,记录此时的破坏面和Tnn。然后改变搜索角,重复上述步骤直到搜索终止。找到一系列Tnn中的最小值,并将此值当作边坡发生整体破坏所需的外力,记录对应的岩层破坏组合和破坏面。
如果Tnn<0(n_startd≤nn≤n_end),那么岩层nn+1受到下部岩层的抵抗力为0。由岩层1~nn组成的破坏面命名为Ωnn,如果岩层nn+1位于破坏面Ωnn上部的等效高度大于岩层在自重作用下的极限高度h0,岩层nn+1将自重作用下发生折断破坏,并且可能发生多次折断破坏。岩层nn+1发生折断破坏的次数可以通过式(30)确定:
| ${n_1} = \left\lfloor { {{\overline h_{nn + 1}}} /{h_0}} \right\rfloor $ | (30) |
同理,岩层nn+2~nt将自重作用下发生折断破坏,折断次数可以通过式(31)确定:
| ${n_{ii}} = \left\lfloor {( {{\overline h_{nn + ii}}} - ( {{\overline h_{nn + ii - 1}}} - {n_{ii - 1}}{h_0}))/{h_0}} \right\rfloor ,\;2 \le ii \le t$ | (31) |
式中,t为岩层在自重作用下发生折断破坏的个数,可以通过式(32)确定:
| $ {{\overline h_{nn + t + 1}}} - {{\overline h_{nn + t}}} + {n_t}{h_0} < {h_0}$ | (32) |
| $nt = nn + t$ | (33) |
式中,nt为破坏岩层总数。于是,边坡整体破坏面由3部分构成:岩层1~nst的剪切破坏面、岩层nst+1~nn的折断破坏面(自重和层间作用力)、岩层nn+1~nt的折断破坏面(仅受自重作用力)。
逐步折减岩体强度参数(黏聚力c、内摩擦角φ、层间内摩擦角φi、抗拉强度σt)使Tnn等于0,此时对应的折减系数FS即为边坡的稳定系数。
当Tnn=0,边坡处于极限平衡状态,稳定系数FS等于1。
如果Tn_end>0,即边坡需要外力才能发生破坏,此时边坡处于安全状态。这种情况下,最关心的是边坡稳定系数。逐步折减岩体强度参数(黏聚力c、内摩擦角φ、层间内摩擦角φi、抗拉强度σt),重复第3.2、3.3节步骤使Tnn=0,记录此时边坡整体破坏面、岩层破坏个数和折减系数FS。
4 算例分析 4.1 数值算例选取皖南反倾向板岩边坡[14]作为工程实例。根据文献[14],边坡参数如表1所示,皖南反倾向板岩边坡示意如图6所示。
 |
| 图6 皖南反倾向板岩边坡示意图 Fig. 6 Schematic profile of slate slope in South Anhui |
使用本文算法,最终求得的结果为:边坡发生倾倒破坏;岩层破坏总数为32,第1~12号岩层发生剪切破坏,其余岩层全部发生弯曲拉裂破坏,其中第27~32号岩层在自重作用下发生折断破坏;岩层发生整体破坏所需外部推力为–1.183 2×106 N,稳定系数为0.960 1,剪切破坏角为15.536 9°。使用Aydan法算出的稳定系数为0.934 2,边坡剩余下滑力为4.678 1×106 N,计算结果列入表2。本文得出的边坡破坏基准面由3部分组成:第1部分由1~12号岩层的剪切破坏面组成,剪切破坏面与岩层法线夹角为15.536 9°;第2部分由13~26号岩层的弯曲拉裂破坏面组成,弯曲倾倒破坏面与岩层法线平行;第3部分由27~32号岩层的弯曲折断面组成,此部分岩层的层间作用力为0,岩层在自重作用下发生折断破坏,最后形成边坡整体破坏面如图7所示。使用本文方法得到的破坏基准面与文献[14]模拟结果(图8)较为接近,证明了本文算法的有效性。Aydan和Adhikary认为反倾向边坡的倾倒破坏面是直线型的,分析时只关注弯曲拉裂破坏,忽略了坡脚剪切破坏,且不考虑节理裂隙,因此得出来的破坏面与实际情况并不相符,本文算法能很好地解决上述方法的缺陷。
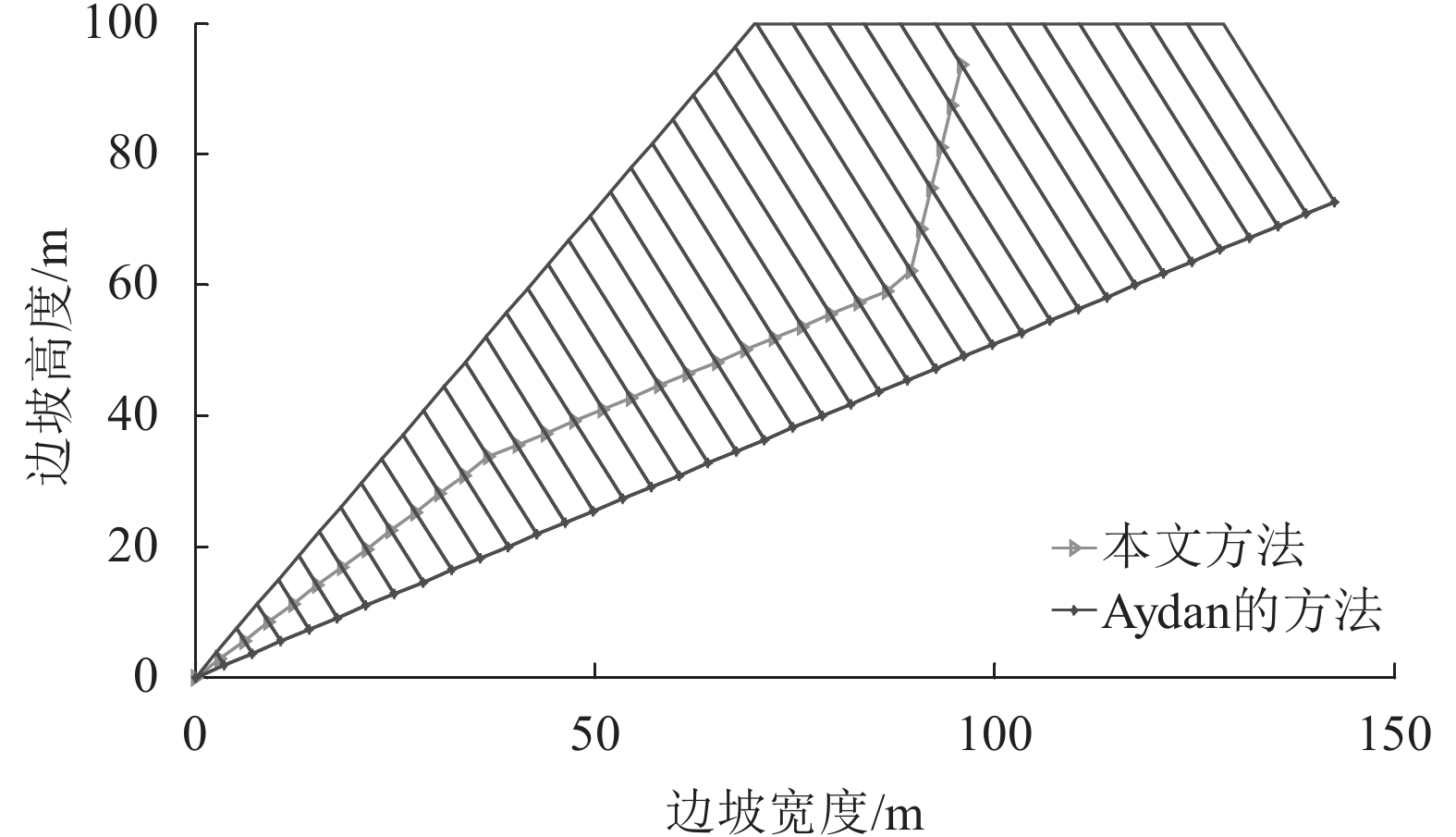 |
| 图7 皖南反倾向板岩边坡破坏面 Fig. 7 Slope failure surface of slate slope in South Anhui |
 |
| 图8 刘海军模拟结果 Fig. 8 Slope failure surface of Liu Haijun |
| 表1 皖南反倾板岩边坡计算参数 Tab. 1 Calculation parameters of slate slope in South Anhui |
 |
| 表2 皖南板岩边坡计算结果对比 Tab. 2 Results comparison of slate slope in south Anhui by different methods |
 |
4.2 节理裂隙对皖南反倾向板岩边坡稳定性的影响
以上述皖南反倾向板岩边坡为数值算例,研究岩层底面节理裂隙长度对边坡稳定性的影响,节理裂隙长度通过不连通率ε反映。不连通率ε的取值与对应计算结果列入表3(边坡其他参数保持不变,如表1所示)。皖南板岩边坡破坏面随不连通率的变化情况如图9所示。
| 表3 不连通率对边坡稳定性的影响 Tab. 3 Calculation results with the changes of non-connectivity rate |
 |
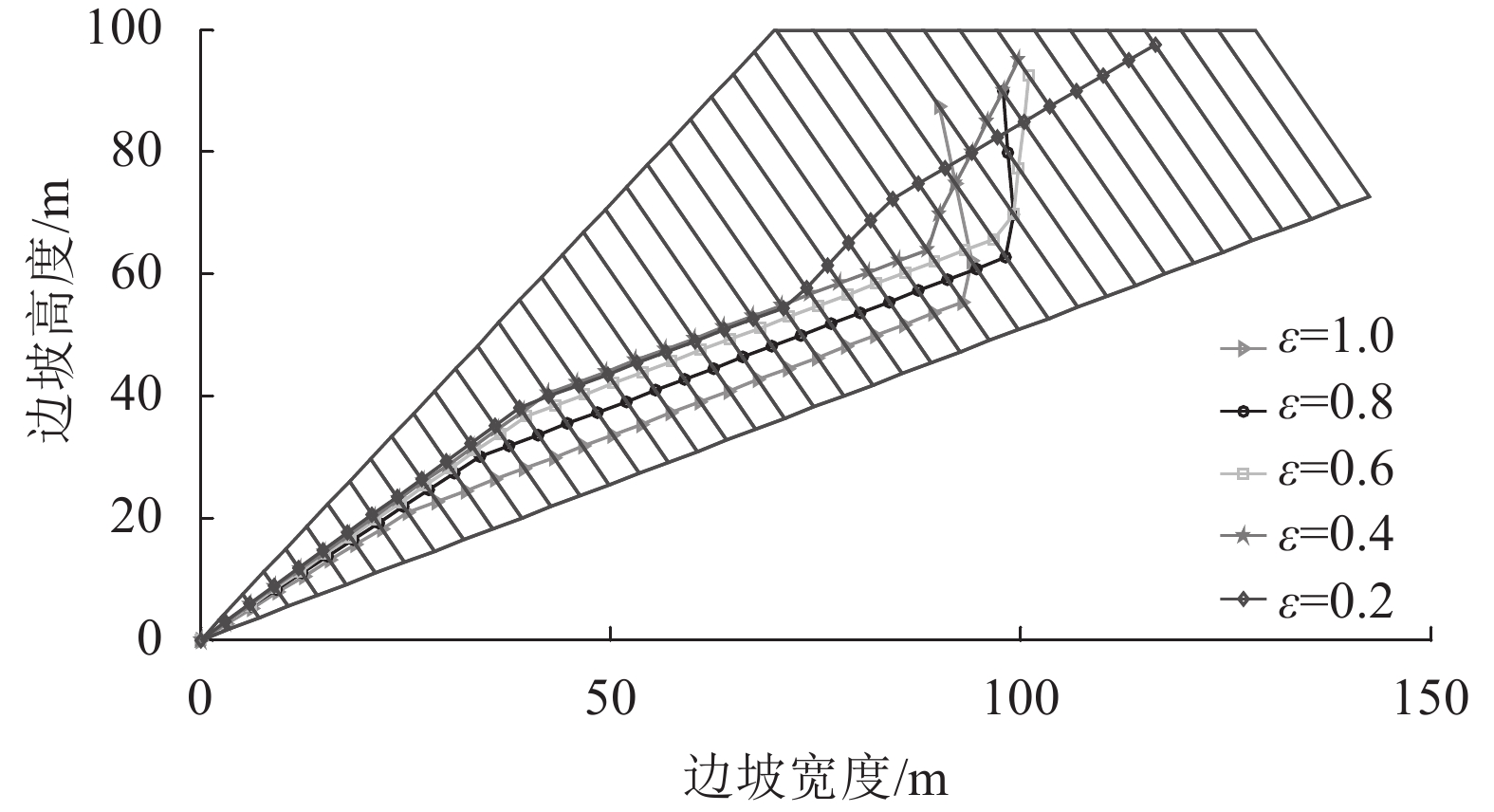 |
| 图9 皖南反倾向边坡破坏面随不连通率变化情况 Fig. 9 Failure surfaces of slate slope in South Anhui with the changes of non-connectivity rate |
从表3和图9可以得出:随着不连通率的减小,发生破坏的岩层总数增大,发生剪切破坏的岩层个数增大,在自重作用下发生折断破坏的岩层数目增多,剪切破坏角增大,边坡在坡体浅部就能发生破坏,边坡愈发不稳定。究其原因,不连通率减小,岩层所能承受的抗拉强度降低,岩层折断高度变小,边坡破坏范围扩大,即岩层破坏总数增大;折断高度减小导致边坡整体破坏位置上移,剪切破坏角增大,破坏岩层的长细比变小,发生剪切破坏的岩层数目增大;边坡愈发不稳定的直接结果使岩层整体破坏所需外力进一步减小,nn变小,岩层在自重作用下发生折断破坏的数目增大。
需要注意的是,用本文方法计算的边坡稳定系数和边坡发生破坏所需最小外力评价边坡稳定性只适用于相同工况的边坡。对于不同工况(不连通率不同)的边坡,如果判定该边坡为失稳边坡,由于不同工况下岩层破坏总数并不相同,仅仅以上述结果评价边坡稳定性是不合适的。此时,应结合边坡剪切破坏角和岩层破坏总数评价该边坡的稳定性。剪切破坏角越大,说明边坡发生破坏深度越浅,边坡孕育累计变形时间越短,边坡更容易发生破坏;岩层破坏总数越大,也即不稳定岩层数目越大,边坡更加不稳定。
5 结 论根据野外实际观测、试验研究和理论分析,本文提出一种搜索弯曲倾倒破坏基准面的计算方法,计算分析时,充分考虑节理裂隙对边坡稳定性的影响。最后结合工程实例证明了本文算法的有效性,并进行了参数分析。主要结论有:
1)对于皖南反倾板岩边坡而言,由于岩层中上部变形空间较小,岩层破坏是从坡脚开始的。岩层破坏方式主要有两种:弯曲拉裂和剪切滑移。其中剪切破坏区主要发生在坡脚区域,岩层中上部主要发生弯曲拉裂破坏。
2)对反倾向层状板岩边坡而言,其破坏基准面主要由多组折线段组成的破坏面。剪切破坏面与岩层法线之间有一定夹角,夹角越大,边坡越不稳定。
3)随着不连通率的减小,发生破坏的岩层总数增大,发生剪切破坏的岩层个数增大,在自重作用下发生折断破坏的岩层数目增多,剪切破坏角增大,边坡愈发不稳定。
| [1] |
Wyllie D C. Toppling rock slope failures examples of analysis and stabilization[J]. Rock Mechanics, 1980, 13(2): 89-98. DOI:10.1007/BF01238952 |
| [2] |
Wang Sijing. On the mechanism and process of slope deformation in an open pit mine[J]. Chinese Journal of Geotechnical Engineering, 1982, 4(1): 76-83. [王思敬. 金川露天矿边坡变形机制及过程[J]. 岩土工程学报, 1982, 4(1): 76-83.] |
| [3] |
Goodman R E,Bray J W.Toppling of rock slopes[C]//Proceedings of the Specialty Conference on Rock Engineering for Foundations and Slopes ASCE.Colorado:Boulder Geotechnical Engineering Division of ASCE,1976:201–243.
|
| [4] |
Aydan O, Shimizu Y, Ichikawa Y. The effective failure modes and stability of slopes in rock mass with two discontinuity sets[J]. Rock Mechanics & Rock Engineering, 1989, 22(3): 163-188. |
| [5] |
Bobet A. Analytical solutions for toppling failure[J]. International Journal of Rock Mechanics & Mining Sciences, 1999, 36(7): 971-980. |
| [6] |
Liu C H, Jaksa M B, Meyers A G. A transfer coefficient method for rock slope toppling[J]. Canadian Geotechnical Journal, 2009, 46(1): 1-9. DOI:10.1139/T08-094 |
| [7] |
Yagoda G B, Hatzor Y H. A new failure mode chart for toppling and sliding with consideration of earthquake inertia force[J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 64(6): 122-131. |
| [8] |
Caine N. Toppling failures from alpine cliffs on ben Lomond,Tasmania[J]. Earth Surface Processes & Landforms, 1982, 7(2): 133-152. |
| [9] |
Aydan O, Kawamoto T. Toppling failure of discontinuous rock slopes and their stabilization[J]. Nippon Kogyo Kaishi/Journal of the Mining & Metallurgical Institute of Japan, 1987, 103(1197): 763-770. |
| [10] |
Aydan O, Kawamoto T. Stability of slopes and underground openings against flexural toppling and their stabilization[J]. Rock Mechanics & Rock Engineering, 1992, 25(3): 143-165. |
| [11] |
Adhikary D P, Dyskin A V, Jewell R J. A study of the mechanism of flexural toppling failure of rock slopes[J]. Rock Mechanics & Rock Engineering, 1997, 30(2): 75-93. |
| [12] |
Aydan O, Amini M. An experimental study on rock slopes against flexural toppling failure under dynamic loading and some theoretical considerations for its stability assessment[J]. Journal of the College of Marine Science & Technology Tokai University, 2009, 7(2): 25-40. |
| [13] |
Cai Jingsen, Yan Echuan, Wang Zhangqiong. Study of cantilever beam limit equilibrium model of anti-dip layered rock slopes[J]. Rock and Soil Mechanics, 2014, 35(增刊1): 15-28. [蔡静森, 晏鄂川, 王章琼. 反倾层状岩质边坡悬臂梁极限平衡模型研究[J]. 岩土力学, 2014, 35(增刊1): 15-28.] |
| [14] |
Liu Haijun.Research on the toppling deformation mechanism of counter-tilt slate slope in the mountainous zone of southern anhui[D].Chengdu:Chengdu University of Technology,2012. [刘海军.皖南山区反倾板岩边坡倾倒变形机理研究[D].成都:成都理工大学,2012.]
|
| [15] |
Wu Faquan. Theoretical analysis of bending and toppling deformation in slopes of micaquartz schist[J]. Journal of Engineering Geology, 1997, 5(4): 306-311. [伍法权. 云母石英片岩斜坡弯曲倾倒变形的理论分析[J]. 工程地质学报, 1997, 5(4): 306-311.] |
| [16] |
Chen Hongqi, Huang Runqiu. Stress and flexibility criterion of bending and breaking in a countertendency layered slope[J]. Journal of Engineering Geology, 2004, 12(3): 243-246. [陈红旗, 黄润秋. 反倾层状边坡弯曲折断的应力及挠度判据[J]. 工程地质学报, 2004, 12(3): 243-246.] |
| [17] |
Jiang Liangwei, Huang Runqiu. Bending yielding and tensile cracking critera for failure of rock slope whose dip direction opposite to the dip direction of stratum[J]. Journal of Engineering Geology, 2006, 14(3): 289-294. [蒋良潍, 黄润秋. 反倾层状岩体斜坡弯曲-拉裂两种失稳破坏之判据探讨[J]. 工程地质学报, 2006, 14(3): 289-294.] |
| [18] |
Lu Haifeng, Liu Quansheng, Chen Congxin. Improvement of cantilever beam limit equilibrium model of counter-tilt rock slopes[J]. Rock and Soil Mechanics, 2012, 33(2): 577-584. [卢海峰, 刘泉声, 陈从新. 反倾岩质边坡悬臂梁极限平衡模型的改进[J]. 岩土力学, 2012, 33(2): 577-584.] |
| [19] |
Chen Congxin, Zheng Yun, Sun Chaoyi. An analytical approach on flexural toppling failure of counter-tilt slopes of layered rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(11): 2174-2187. [陈从新, 郑允, 孙朝燚. 岩质反倾边坡弯曲倾倒破坏分析方法研究[J]. 岩石力学与工程学报, 2016, 35(11): 2174-2187.] |
| [20] |
Chen Z Y. A generalized solution for tetrahedral rock wedge stability analysis[J]. International Journal of Rock Mechanics & Mining Sciences, 2004, 41(4): 613-628. |
| [21] |
潘家铮.建筑物的抗滑稳定和滑坡分析[M].北京:水利出版社,1980.
|
| [22] |
Sun Guangzhong, Zhang Wenbin. A commonly-sighted rock mass structure-slab-rent structure and its mechanical model[J]. Chinese Journal of Geology, 1985, 26(3): 275-282. [孙广忠, 张文彬. 一种常见的岩体结构-板裂结构及其力学模型[J]. 地质科学, 1985, 26(3): 275-282.] |
| [23] |
Hoek E,Bray G.Rock slope engineering[M].3rd Edition.London:Institute of Mining and Metallurgy,1981.
|
| [24] |
Zhang Z L, Wang T, Wu S R. Rock toppling failure mode influenced by local response to earthquakes[J]. Bulletin of Engineering Geology & the Environment, 2016, 75(4): 1361-1375. |
| [25] |
Alzo’ubi A K, Martin C D, Cruden D M. Influence of tensile strength on toppling failure in centrifuge tests[J]. International Journal of Rock Mechanics & Mining Sciences, 2010, 47(6): 974-982. |
 2017, Vol. 49
2017, Vol. 49


