2. 福州大学 数学与计算机科学学院,福建 福州 350108
2. College of Mathematics and Computer Sci., Fuzhou Univ.,Fuzhou 350108,China
短时冻土区(冻结时间在数小时至数日)广泛分布在中国长江以南,珠江流域以北地区,面积约1.9×106 km2[1]。2008年中国南方发生的百年一遇的极端冰雪灾害中,由于高强度降雪及冰雪融化引起的滑坡等地质灾害达3 106处[2]。2012年福建省S303线武夷山境内约40 km范围内35处花岗岩残积土边坡因冰雪融化出现浅层失稳,严重影响公路正常运营。由此可见,短时冻区内冰雪消融入渗是诱发边坡在降雨量较少的冬季出现大量失稳现象的主要因素之一。
目前,国内外学者已针对冰雪消融入渗及其对边坡稳定性的影响进行了大量研究,并取得了许多有价值的研究结论。如Swanger等将夏季土壤表面平均温度(MSSST)按照1维热扩散方程统计融化深度变化量,并用摩尔–库伦安全系数准则进行浅层稳定性分析[3]。Charles等以土坡比例模型试验为基础对正融滑坡进行研究[4]。殷坤龙等调研了北欧瑞士地区的冰雪融化入渗诱发滑坡失稳现象并分析了成因机理[5]。吴玮江研究认为中国季节性冻区的冰雪消融,能扩大土体软化范围,降低土体强度[6]。张永兴、张连勇等认为冰雪入渗边坡冻土后结冰对土壤产生冻胀作用,同时融雪沿边坡裂隙的渗流作用易使边坡原有平衡被破坏[7–8]。郑长安等采用数值模拟分析积雪入渗时诱发浅层滑坡机理[9]。缪海波等认为积雪长时间覆盖于植被发育的边坡,容易影响植物根系对于土壤的固定作用,减弱边坡土体的抗滑力[10]。
值得注意的是,以上成果分析大多集中于多年与季节冻土及基于非饱和渗流理论进行融雪入渗分析。事实上,相较于多年与季节冻土,南方短时冻区内的冰雪消融诱发残积土边坡失稳现象,具有以下鲜明特征:1)虽然冬季降雪量较小,冰雪厚度(通常小于10 cm)不大,但该区域内昼夜温差大,冰雪易在短时间(通常1~2 d)内消融,其融雪入渗强度较高。例如2014年福建武夷山地区融雪入渗强度大约为20~30 mm/d。2)花岗岩残积土具有孔隙率大的特点(如花岗岩残积土大孔隙比例达2.40%~48.72%[11]),加上短时冻区内反复冻融循环对土体的胀缩作用,导致土壤中大孔隙数目明显增多。土壤大孔隙中的水流可绕过周围大部分土壤基质而短时间内到达土壤深层,即产生非平衡流[12],此时的非均质流土壤水分的流速和流量远大于达西定律描述的运动特性。
研究表明,考虑非平衡流的土壤湿润锋下降速度比传统非饱和渗流快3~8倍,说明传统的Darcy定律并不能准确描述短时冻区内冰雪消融条件下边坡非平衡渗流机理。因此,近年来非平衡流方面研究已成为国内外学者的热点领域之一。虽然目前描述水分在含大孔隙土壤中运移的理论模型有多种,如两域模型、多域模型、2阶段模型等[8],但上述模型主要集中于水平面1维入渗,尚未进行斜坡入渗及考虑非平衡流的边坡稳定性研究,因而无法准确描述短时冻区冰雪消融在含大孔隙斜坡的渗流特性,进而无法从理论上为揭示斜坡浅层失稳机理提供支撑。
鉴于此,以福建省短时冻区融雪诱发某一边坡失稳为例,初步尝试基于水分非平衡流控制方程与极限平衡理论,采取数值模拟与室内试验相结合的方法,借助Hydrus 2D/3D软件的Dual-Permeability模块与SLOPE模块,实现冰雪消融条件下残积土平衡流模拟及边坡稳定性分析,从而为短时冻区冰雪消融诱发边坡失稳提供理论依据。
1 研究区边坡概化模型以福建省省道303线某残积土路堑边坡为工程地质原型,该边坡位于短时冻区,于2014年1月8日在融雪过程产生浅层滑塌,最大滑深约2 m。经现场勘察得边坡高6 m,坡度约为45°,边坡岩土体由上而下依次为砂质黏土、粉质黏土2层,未发现不良地质,具体地质剖面概化模型如图1所示。
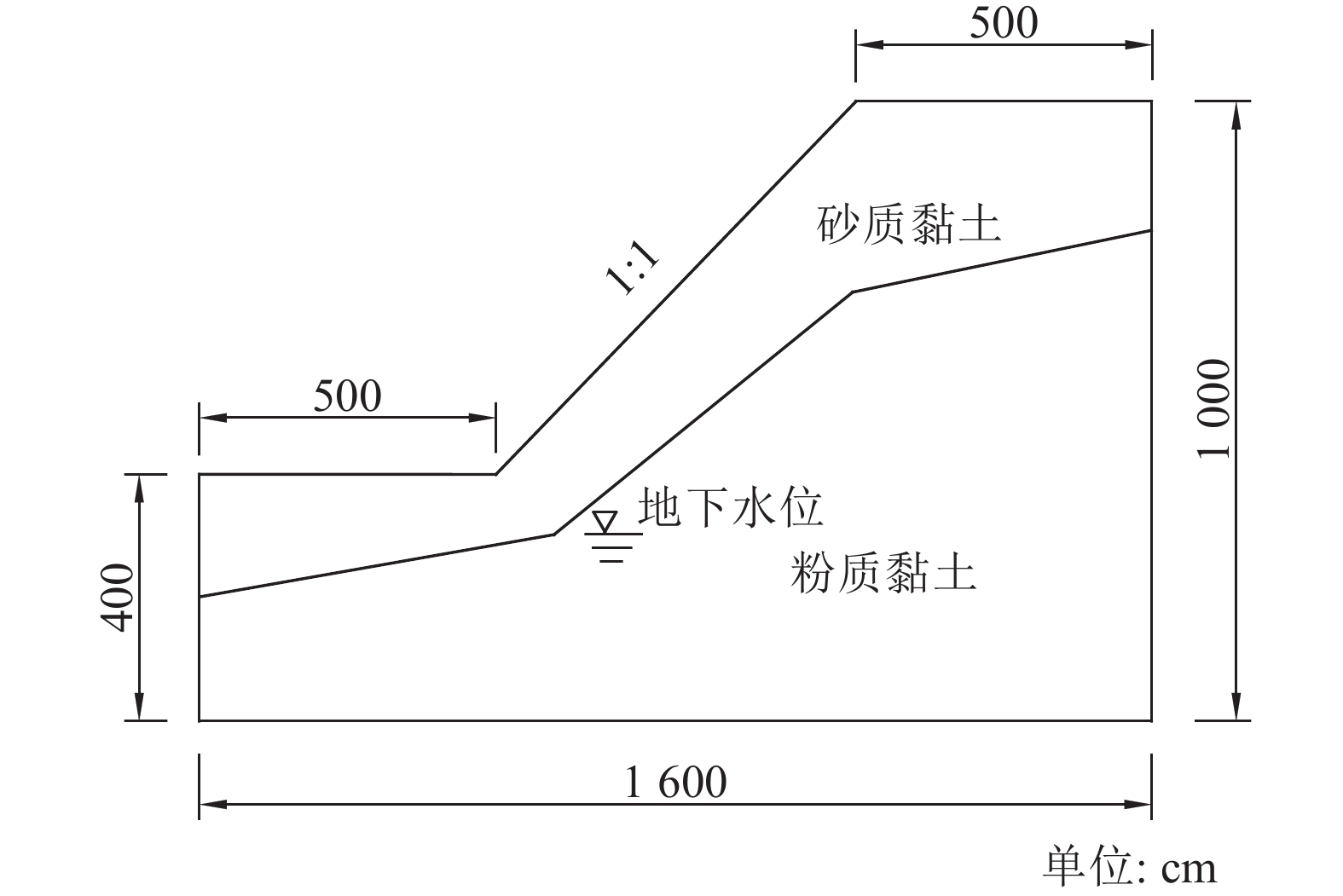 |
| 图1 边坡概化模型 Fig. 1 Geological model |
2 边坡非平衡流与稳定性分析模型 2.1 非平衡渗流方程
假定残积土不发生收缩与膨胀,密度保持一致,无滞留现象发生,忽略大气压、溶质浓度及温度对水分运移的影响,以水头为变量的大孔隙域与基质域的水流下渗方程如式(1)~(2)所示[13]。
| ${C_{\rm f}}\frac{{\partial h}}{{\partial t}} = \frac{\partial }{{\partial \textit{z}}}\left( {{K_{\rm f}}\frac{{\partial {h_{\rm f}}}}{{\partial {\textit{z}}}} + {K_{\rm f}}} \right) - \frac{{{\varGamma _{\rm w}}}}{{{\omega _{\rm f}}}}$ | (1) |
| ${C_{\rm m}}\frac{{\partial h}}{{\partial t}} = \frac{\partial }{{\partial \textit{z}}}\left( {{K_{\rm m}}\frac{{\partial {h_{\rm m}}}}{{\partial {\textit{z}}}} + {K_{\rm m}}} \right) + \frac{{{\varGamma _{\rm w}}}}{{1 - {\omega _{\rm f}}}}$ | (2) |
式中:t为时间,s;wf为大孔隙域与整个土体的体积比;h为压力水头,m;K为非饱和导水率,m/s;
根据冰雪消融条件下边坡渗流场的结果计算地下水位以上非饱和带岩土强度的定量变化,采用Fredlund岩土强度理论[14],具体为:
| ${\tau _{\rm f}} = {c'} + \left( {{u_{\rm a}} - {u_{\rm w}}} \right)\tan\; {\varphi ^{\rm b}} + \left( {\sigma - {u_{\rm a}}} \right)\tan\; {\varphi '}$ | (3) |
式中:τf为剪应力,单位为kPa;
计算初始条件的选取分为2种:1)验证室内非平衡流模型试验结果时,以含水率分布为初始条件,基于现场实测含水率,将边坡初始含水率统一为19.5%。2)分析融雪入渗下边坡稳定性时,为模拟更真实边坡水分场,以压力水头为初始条件,地下水位选取如图2所示。其中,0 cm地下水位线以下为饱和土体,因而其压力水头随深度的增加呈正增长;0 cm地下水位线以上为非饱和土体,根据非饱和土力学理论,非饱和区域其孔隙水压力为负值;因此,0 cm地下水位线以上为负值,且数值逐渐减小。
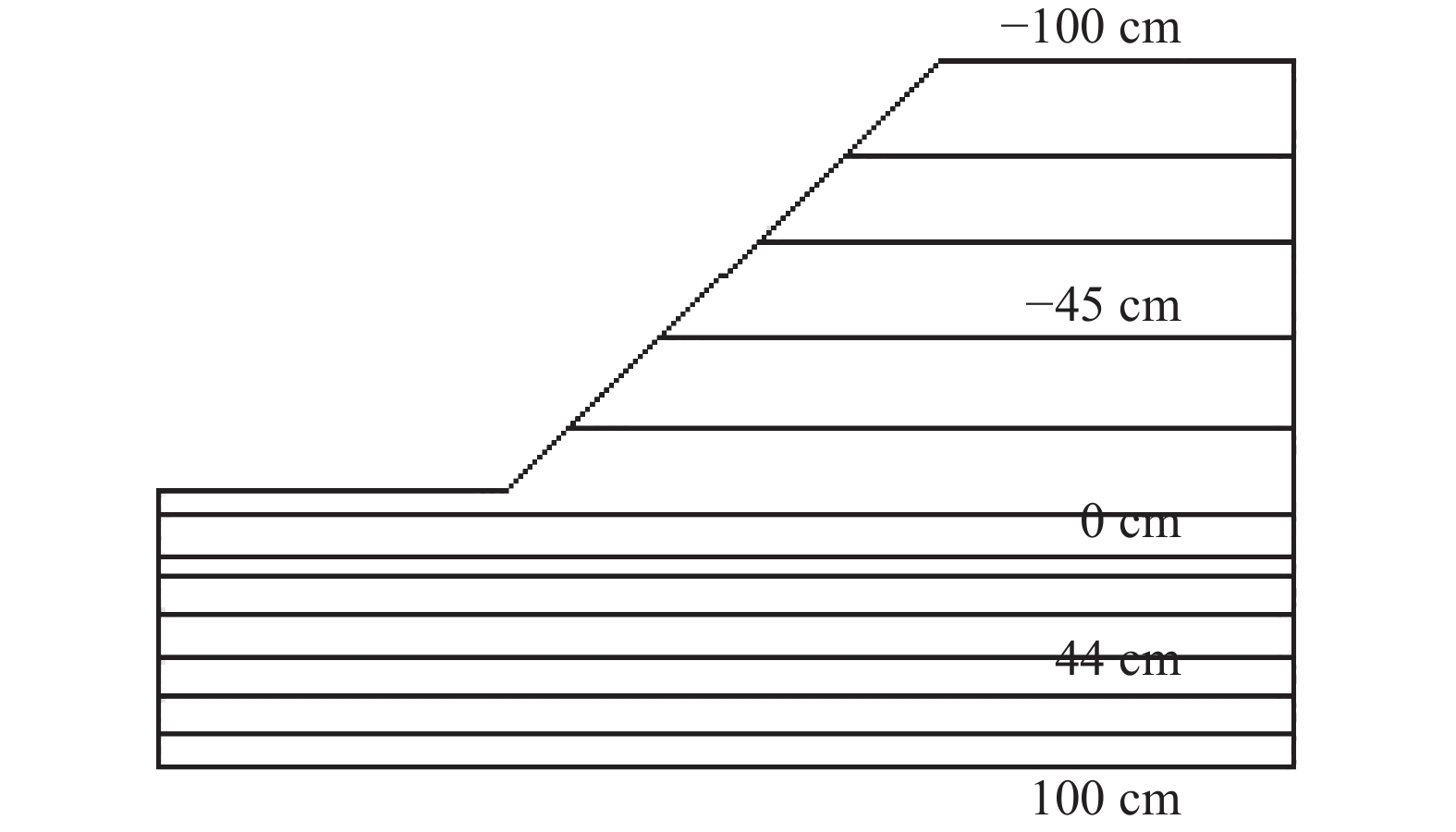 |
| 图2 边坡初始孔压水头 Fig. 2 Distribution of initial pore water pressure |
边界条件分2种:1)验证室内非平衡流的模型试验结果时,边坡面上积雪区域采用大气边界模拟,非覆雪区域采用渗透面边界,两侧采用零通量边界,底部采用自由排水边界[15],见图3。2)分析融雪入渗下边坡稳定性时,地下水位以下采用定水头边界,地下水位以上及底部采用零通量边界,边坡面上边界设置与第1种情况一致[16]。
 |
| 图3 非平衡流模型试验边界 Fig. 3 Boundary on test of non-equilibrium flow |
2.4 计算参数
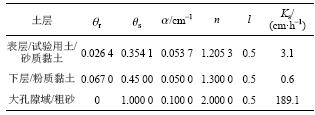
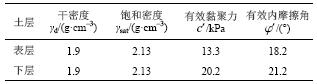
土样源自研究区边坡,其非饱和土层的水分参数主要通过滤纸法测得含水率与吸力的关系,并对van Genuchten模型[17](式(4))参数进行标定,如表1所示。同时对现场土样进行室内物理力学参数试验,其中有效强度指标采用三轴试验得到,如表2所示。
| $\theta (H) = \left\{ \begin{array}{l}{\theta _{\rm r}} + \displaystyle\frac{{{\theta _{\rm s}} - {\theta _{\rm r}}}}{{{{\left[ {1 + {{\left| {\alpha H} \right|}^n}} \right]}^m}}}\text{,}H &< 0\text{;}\\[7pt]{\theta _{\rm s}}\text{,}H \ge 0\end{array} \right.$ | (4) |
式中:
| 表1 非饱和土层及大孔隙域水分参数 Tab. 1 Hydraulic parameters of soil |
 |
| 表2 不同土层的物理力学参数 Tab. 2 Physical and mechanical parameters of soil |
 |
2.5 冰雪消融条件下非平衡渗流试验与数值模拟对比 2.5.1 试验设计
模型试验箱采用有机玻璃土箱,其尺寸与埋设TDR土壤水分传感器的开孔位置如图4所示。模箱底部开3个直径为50 mm的圆孔用于排水。大孔隙直径分为6、10 mm两种工况。试验步骤如下:
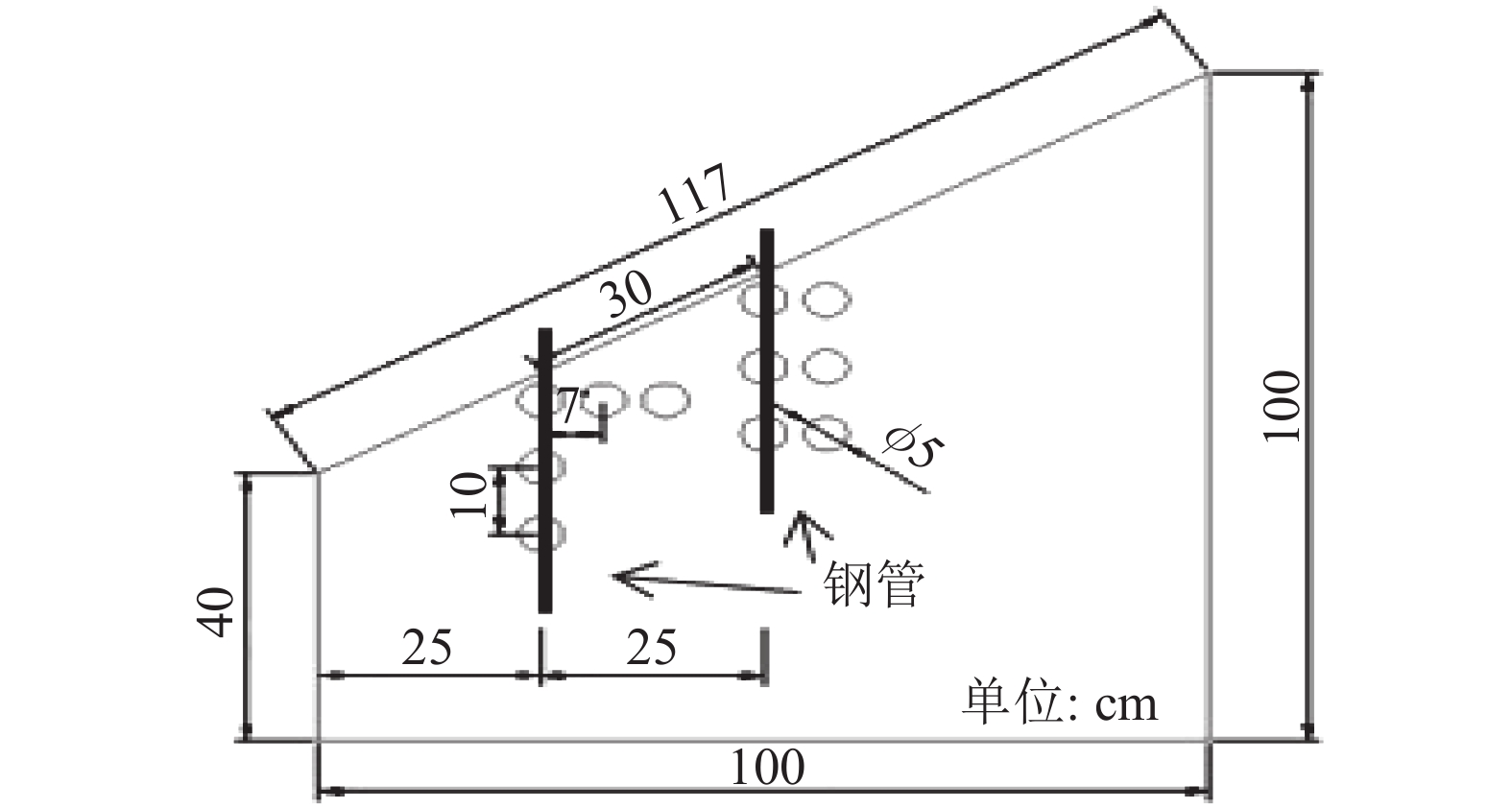 |
| 图4 模箱试验槽 Fig. 4 Box of model test |
1)填土前先在模箱底部铺一层纱布,作为反滤层,模拟自由排水边界;前后两面均密闭,模拟不透水边界。
2)残积土(来源于研究区边坡)装填采取分层填充,每隔5 cm夯实一次,控制压实度为85%左右;待填土高度距坡面位置35 cm时,按照图5中的位置插入2根定制细钢管,然后继续进行分层填土夯实,待残积土装填压实完成后,放置一段时间,将细钢管拔掉,往其中孔洞中填满粗砂,用以模拟大孔隙域[18]。
 |
| 图5 大孔隙域填充模拟 Fig. 5 Model of macropore |
3)分层填筑夯实后,将11个TDR土壤水分传感器的探针按照图4(对应图6中编号1~11)所示位置依次埋入各孔洞中,用于记录各时刻相应位置深度的土壤含水率。其中1、2、3测点分别代表近坡脚处大孔隙域5、15、25 cm深度处;4、5测点为5 cm深度处,距离大孔隙7、14 cm的基质域;6、7、8测点为坡中处大孔隙域5、15、25 cm深度处;9、10、11测点分别为距离大孔隙7 cm处各深度的基质域,如图6所示。
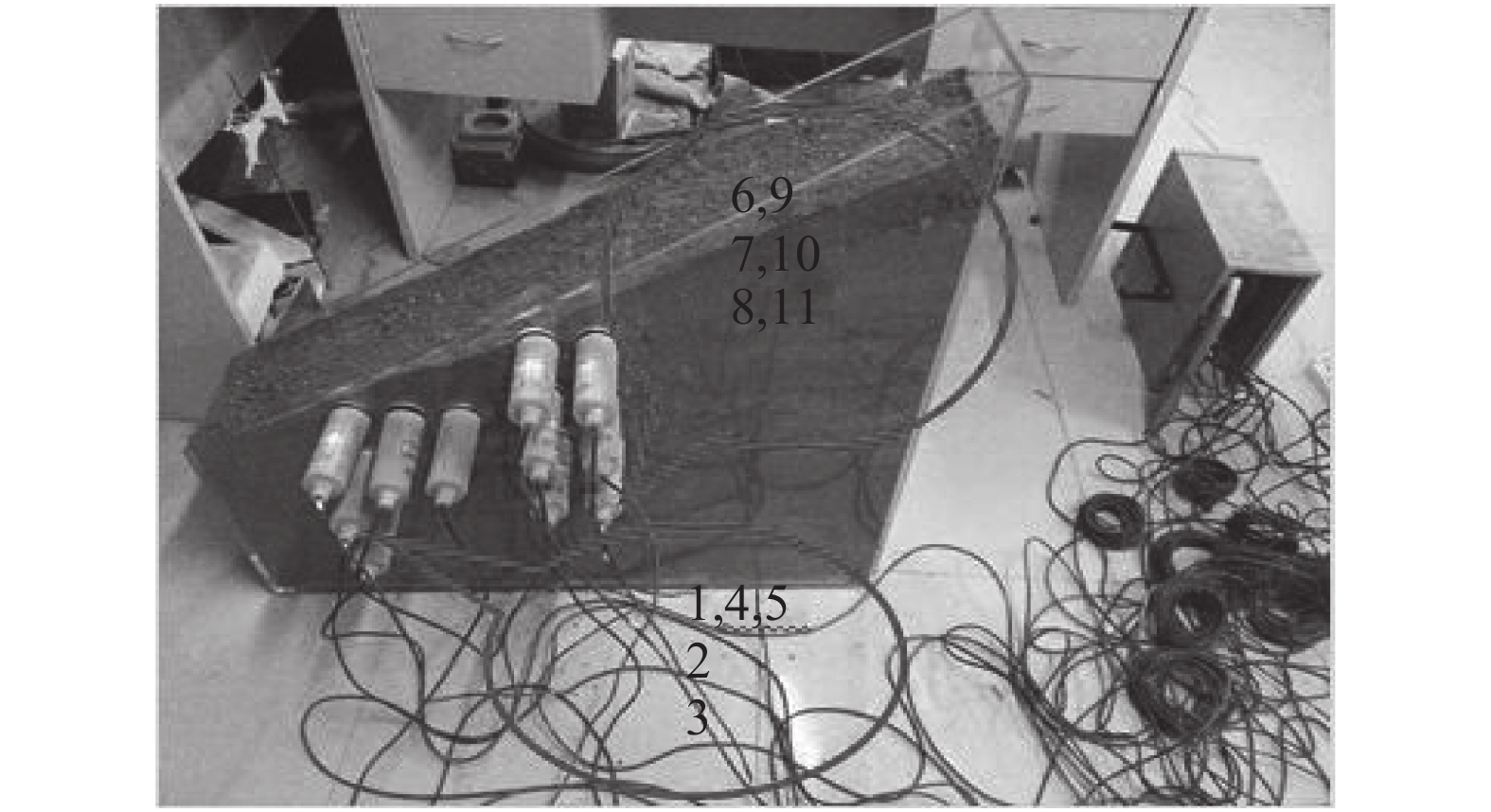 |
| 图6 TDR传感器埋设 Fig. 6 Layout of TDR probes |
4)采用与覆雪深度相对应厚度的冰块模拟冰雪消融入渗,冰块厚度为30 mm,如图7所示。本次监测时长为12 h,其中冰雪融化时长约6 h,其冰雪消融入渗强度为5 mm/h左右。水分传感器采用土壤墒情监测站进行实时数据采集,采集频率为10 min一次。
 |
| 图7 含水率监测过程 Fig. 7 Moisture content measurement |
2.5.2 试验结果
图8~9分别为不同大孔隙直径条件下(直径为10、6 mm)残积土边坡内大孔隙域与基质域含水率的监测结果。
 |
| 图8 边坡内两域含水率变化(直径为10 mm) Fig. 8 Changes of moisture content between two domains (diameter of macropore is 10 mm) |
 |
| 图9 边坡内两域含水率变化(直径为6 mm) Fig. 9 Changes of water content between two domains (diameter of macropore is 6 mm) |
1)各工况下,室内试验与数值模拟的含水率随时间变化曲线基本吻合,其误差值最大为3.6%,说明所建立的数值模型能够较好地模拟非平衡渗流。
2)大孔隙直径由6增加至10 mm时,大孔隙域5、15、25 cm 3个不同深度处的含水率均出现一定程度的下降,且5 cm深度处含水率的降幅高于15及25 cm深度处约2%。
3)相同深度处大孔隙内的含水率变化速率与峰值明显大于普通基质域,表现为端部大孔隙内的含水率由0迅速增加所达到的含水率峰值的51%左右,远大于基质域含水率峰值,差值为18.3%。试验结束(12 h后)时大孔隙域最终含水率约为24.2%,低于基质域的含水率。同时,距离大孔隙域水平距离7 cm处基质域的含水率变化速率及峰值均高于14 cm处基质域土壤,如入渗的响应时间提前了2.5 h,前者含水率峰值比后者高3.2%。
2.6 研究区边坡失稳分析如图10所示,分别对无大孔隙分布的普通非饱和残积土边坡、考虑大孔隙的残积土边坡在冰雪消融条件下渗流进行分析。模型中大孔隙长度、直径和水平间距等主要依据现场边坡裂缝和坡面植被调查结果,同时鉴于坡面裂缝、植被根系发育及大孔隙域分布的复杂性,采用近似假定的方法,将大孔隙长度取1.5 m,直径取10 mm,水平间隔为1 m,得到不同入渗条件下不同时刻的边坡各点含水率分布如图11、12所示。
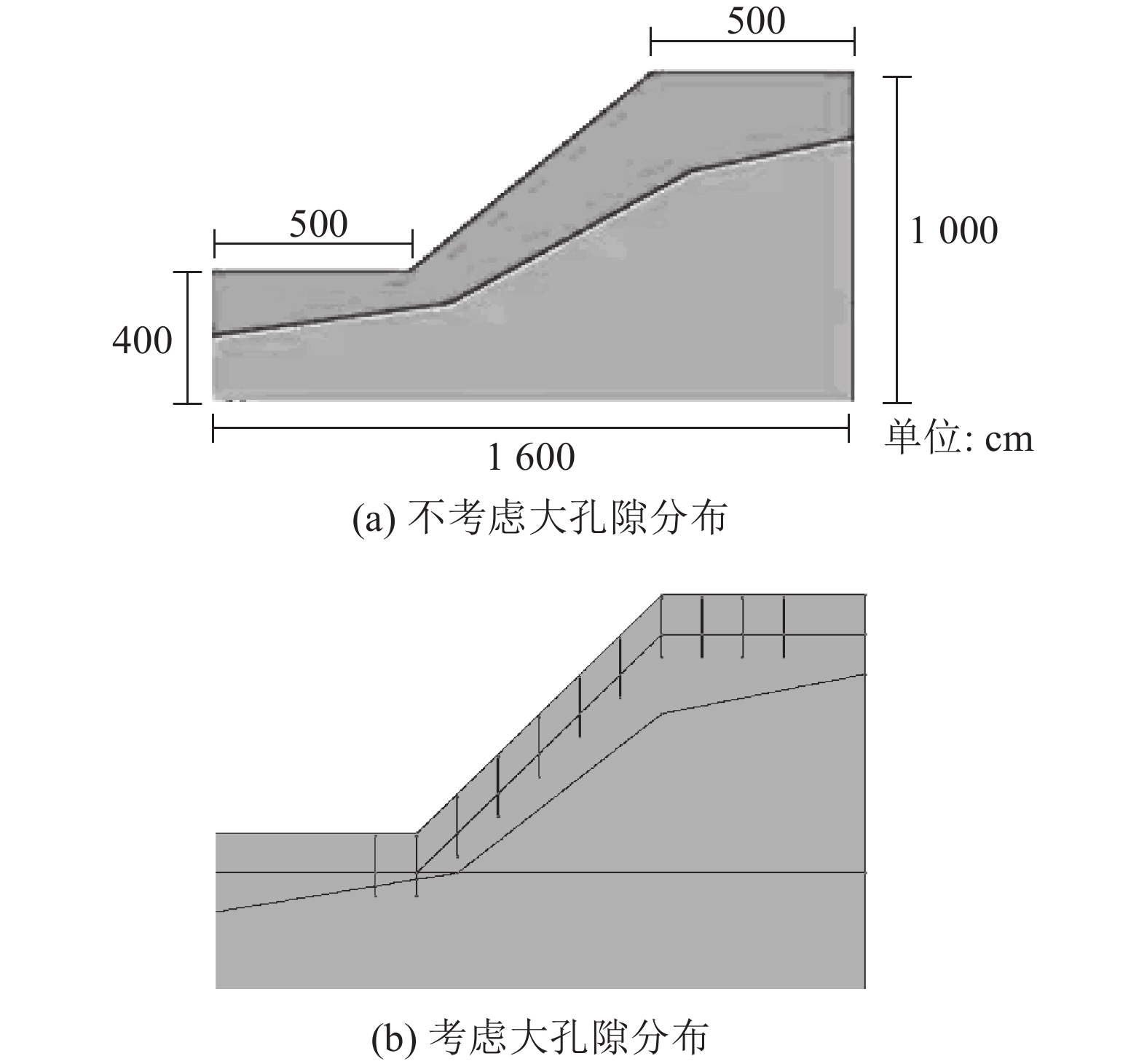 |
| 图10 数值模型 Fig. 10 Numerical model |
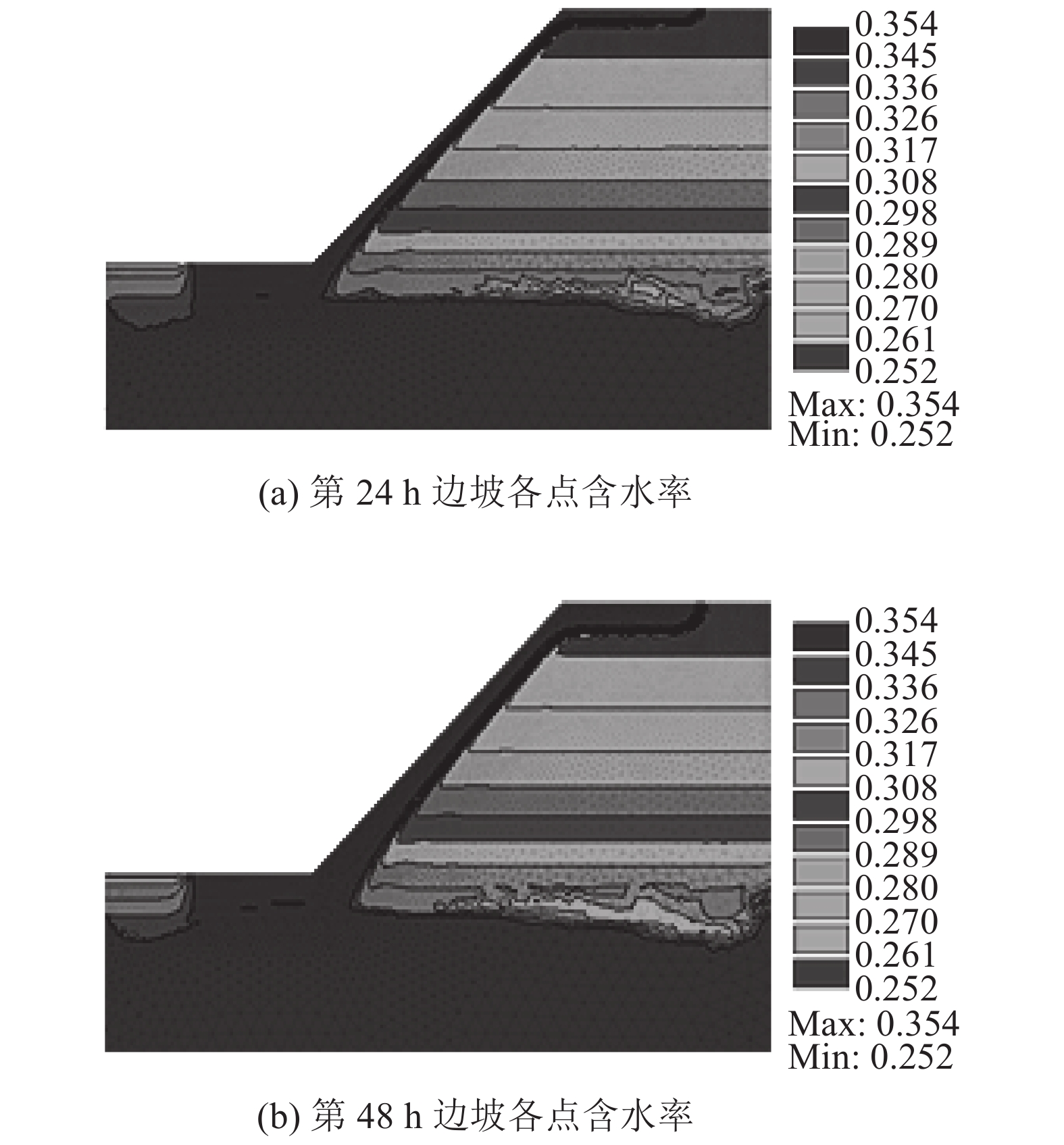 |
| 图11 非饱和渗流下不同时刻边坡含水率 Fig. 11 Water content of slope considering unsaturated seepage |
 |
| 图12 非平衡渗流下不同时刻边坡各点含水率 Fig. 12 Water content of slope considering non-equilibrium flow |
通过调研可知,闽北短时冻区的冰雪消融入渗强度约为30 mm/d;冰雪消融时间多为雪后2~3 d[19–20],因此本次模拟将冰雪消融持时设为48 h。由图11、12可得:
1)非饱和入渗过程中,由于边坡坡脚位置靠近于地下水位线,在12 h时,坡脚区域土体部分趋于饱和,而坡面与坡顶区域湿润锋扩展不明显;第24 h后,表层饱和区域与压力水头开始逐渐增大;至第48 h,边坡坡脚处土体基本处于饱和,坡中、坡顶的饱和土层接近0.5 m,地下水位出现一定上升。
2)非平衡流入渗初期,湿润锋扩展不明显,边坡表层含水率总体变化与非饱和渗流一致;从第6 h开始,大孔隙对水分的优先传导作用开始体现,表层相同深度内大孔隙内的含水率增长速度明显快于基质域,如第24 h时近坡脚处大孔隙底端含水率已趋于饱和状态;当入渗结束(48 h),土体表层近0.5 m深度接近饱和,而在大孔隙位置,湿润锋已拓展至近1 m深度,湿润锋内相同深度处大孔隙域含水率、压力水头明显高于基质域。
通过HYDRU2D/3D中Dual-Permeability等模块计算得到2种渗流情况的水分场后,分别导入HYDRUS/SLOPE模块,得到2种渗流条件下边坡安全系数值随时间的变化规律。图13、14分别为2种渗流条件下在第48 h最危险滑裂面位置。图15为2种渗流条件下边坡安全系数值随时间的变化规律。
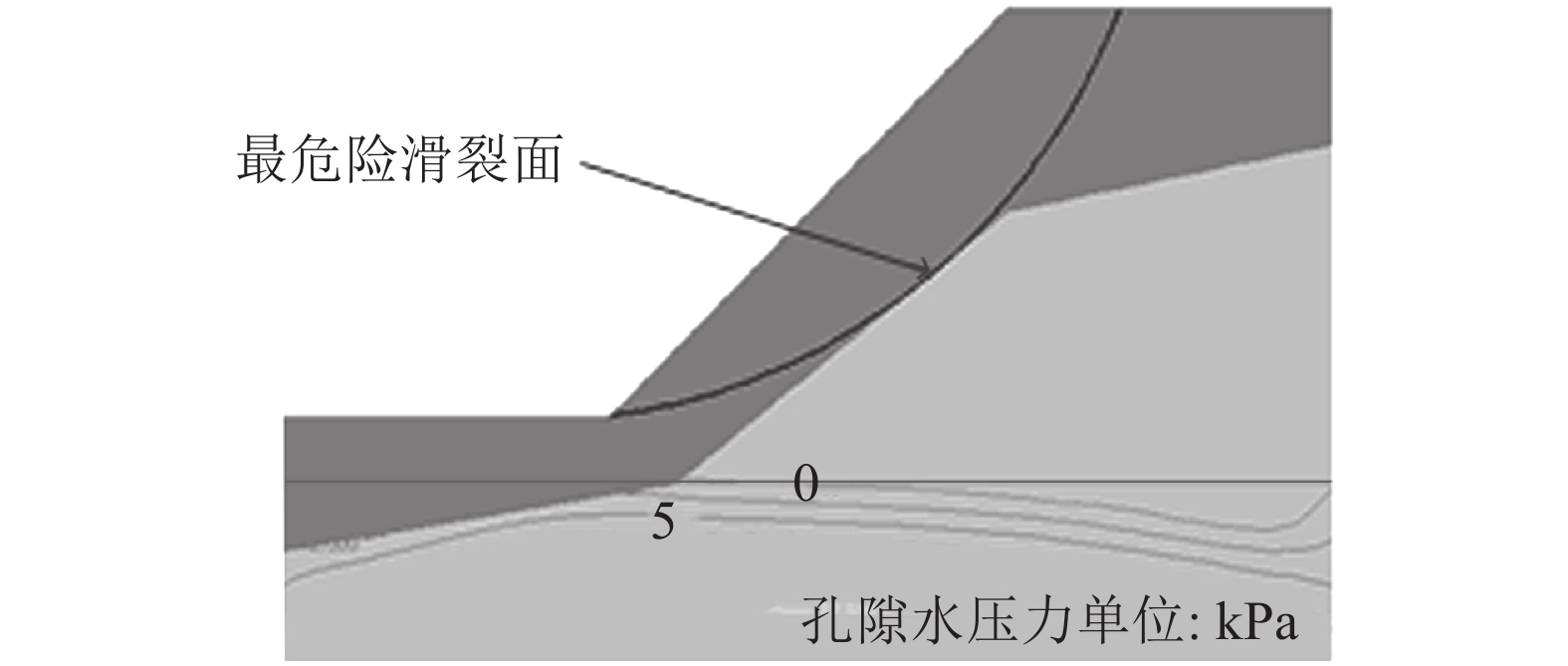 |
| 图13 非饱和渗流第48 h最危险滑裂面 Fig. 13 Slip-surface of slope considering unsaturated seepage at the end of 48th hour |
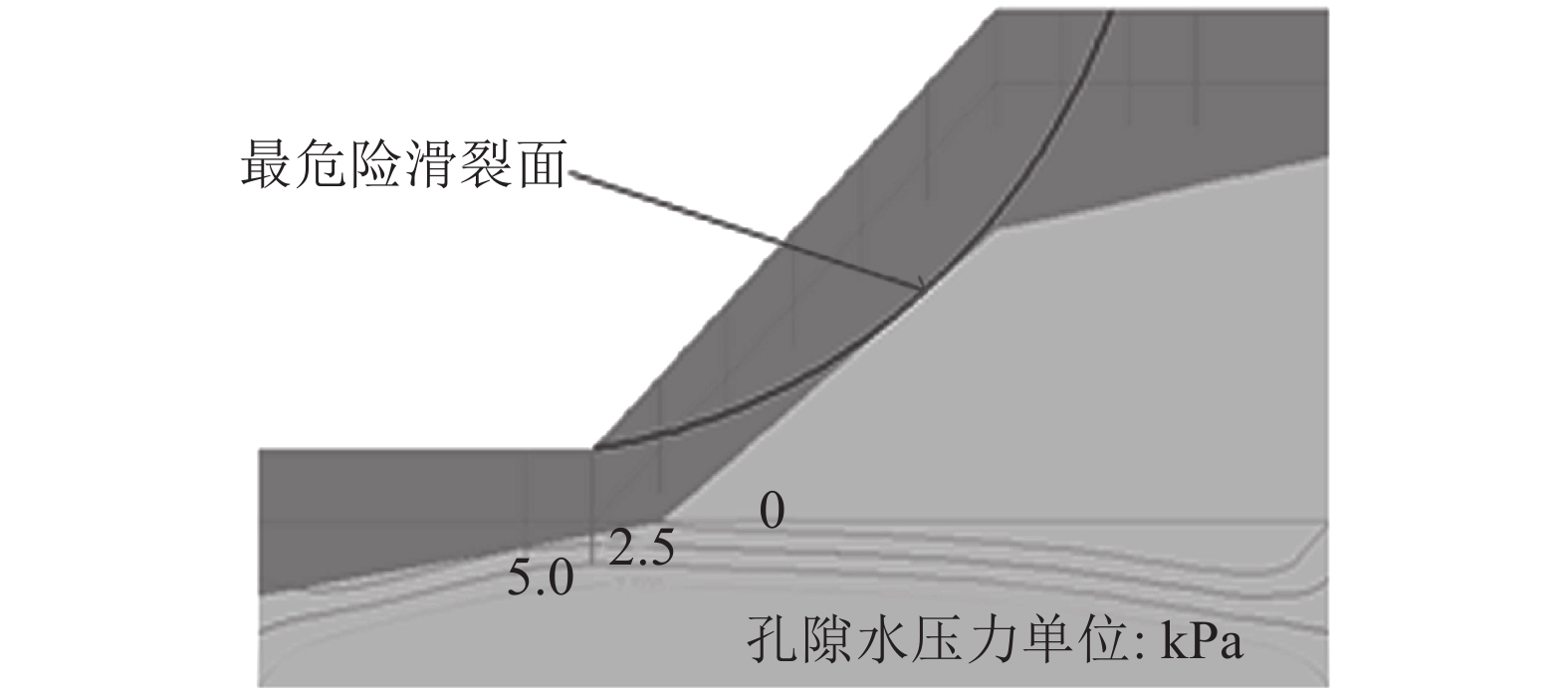 |
| 图14 考虑大孔隙渗流第48 h最危险滑裂面 Fig. 14 Slip-surface of slope considering non-equilibrium flow at the end of 48th hour |
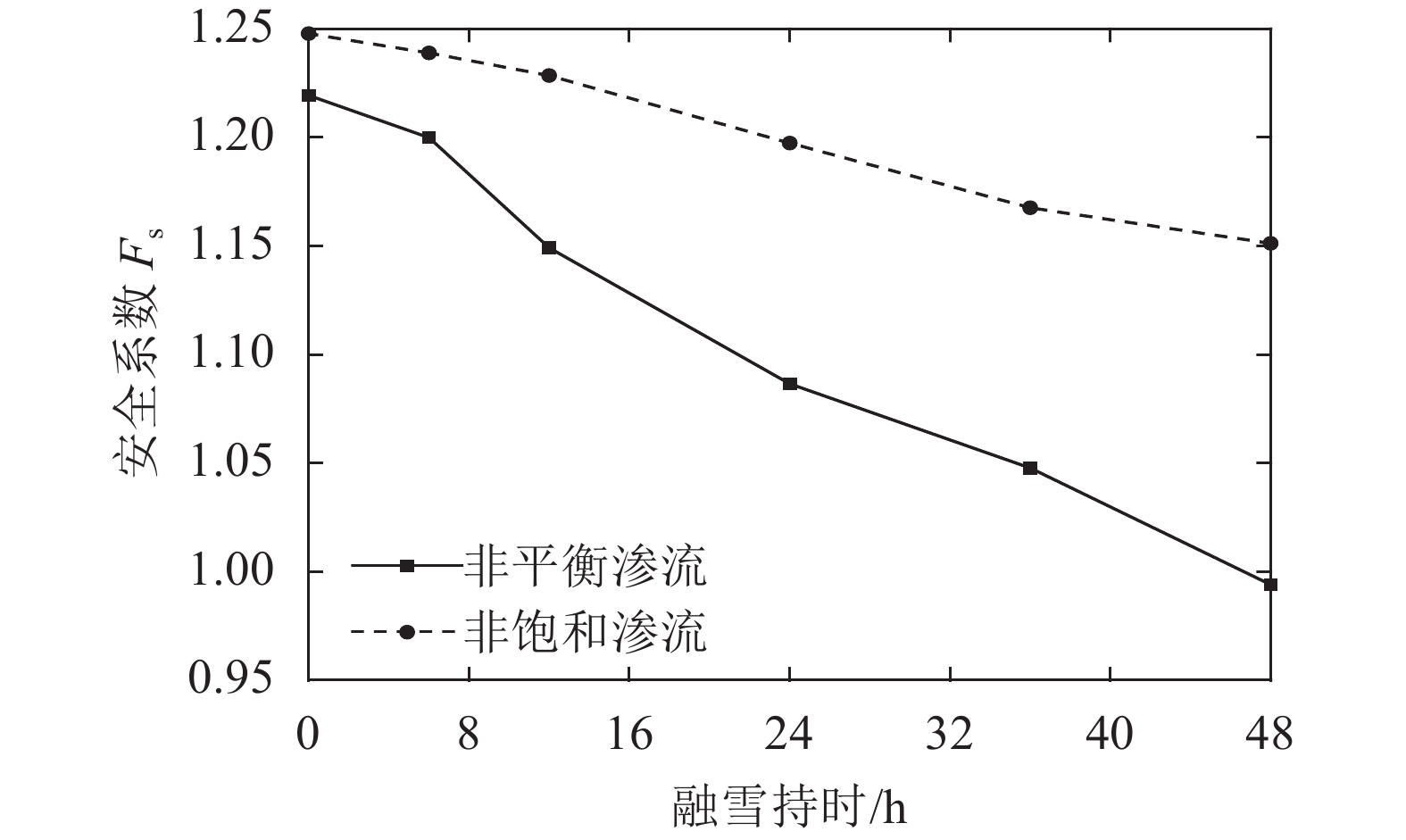 |
| 图15 边坡安全系数随时间的变化 Fig. 15 Relationship between safety factor and snowmelt duration |
由图13~15可知:2种渗流条件下,边坡危险滑裂面均出现在边坡表层,其中非饱和渗流整个入渗过程中,安全系数从1.25下降至1.16,下降幅度为6.9%,但仍满足《公路路基设计规范要求(2015)》中对于2级公路路堑边坡要求(>1.15),边坡处于稳定状态;非平衡渗流过程中,安全系数从1.22下降至0.99,下降幅度为14.8%,不能满足相应规范要求,因而边坡属于不稳定状况。由此说明,非平衡渗流相比于非饱和渗流对于边坡稳定性影响明显更大。对于本失稳边坡工程,未发现不良地质,但坡面植被根系十分发育,大孔隙所占比例大,冰雪融化后容易在坡面层产生非平衡流。因此,如采用非饱和渗流理论,并不能合理解释边坡出现垮塌现象,但采用非平衡流理论可合理解释冰雪消融条件诱发边坡失稳机理。鉴于此,在实际工程中,对于冰雪消融诱发含大孔隙边坡的失稳,应予以重点考虑非平衡流的影响。当然,对于本次失稳分析,仅近似假定大孔隙间距、长度等,具体这些参数在工程中如何设置还需进一步研究。
3 参数影响分析为揭示大孔隙参数对边坡非平衡流与稳定性的影响规律,仍以研究区边坡概化模型为例,分析大孔隙直径、间距、弯曲率及长度对考虑非平衡流的边坡水分场与安全系数的影响。
3.1 大孔隙直径的影响 3.1.1 大孔隙直径对边坡水分场的影响分别选取大孔隙直径d为10、15、20 mm这3种工况,其余条件不变,分析3种工况下大孔隙域内不同深度处含水率随时间的变化过程如图16所示。
 |
| 图16 不同大孔隙直径下各深度含水率变化 Fig. 16 Relationship between water content and diameter of macropore |
由图16可知:
1)冰雪消融期间内,大孔隙域含水率随着大孔隙直径的增加而递减;在冰雪消融结束后,直径变化对于各点含水率的影响不明显。
2)随着大孔隙深度的增加,其相应位置的含水率对于冰雪消融入渗的响应明显滞后,如在25 cm深度处,响应时间由第3 h推迟至第24 h;同时直径的变化对于滞后现象的影响作用可忽略不计。大孔隙直径对于大孔隙含水率的影响作用是由于大孔隙直径的增加,增加了与周围基质域的水分交换,从而降低了各点含水率。
3)随着大孔隙直径增大,距离大孔隙域5 cm处各基质域含水率出现一定增长;在25 cm深度处,含水率的最大差值为1.05%。这表明大孔隙直径增大,使大孔隙域与基质域之间的水分交换增加,且水分交换随深度的增加有所增大。
3.1.2 大孔隙直径对边坡稳定性的影响分别选取大孔隙直径为10、15、20 mm这3种工况,其余条件不变,得到不同大孔隙直径下边坡安全系数随冰雪消融过程的变化如图17所示。
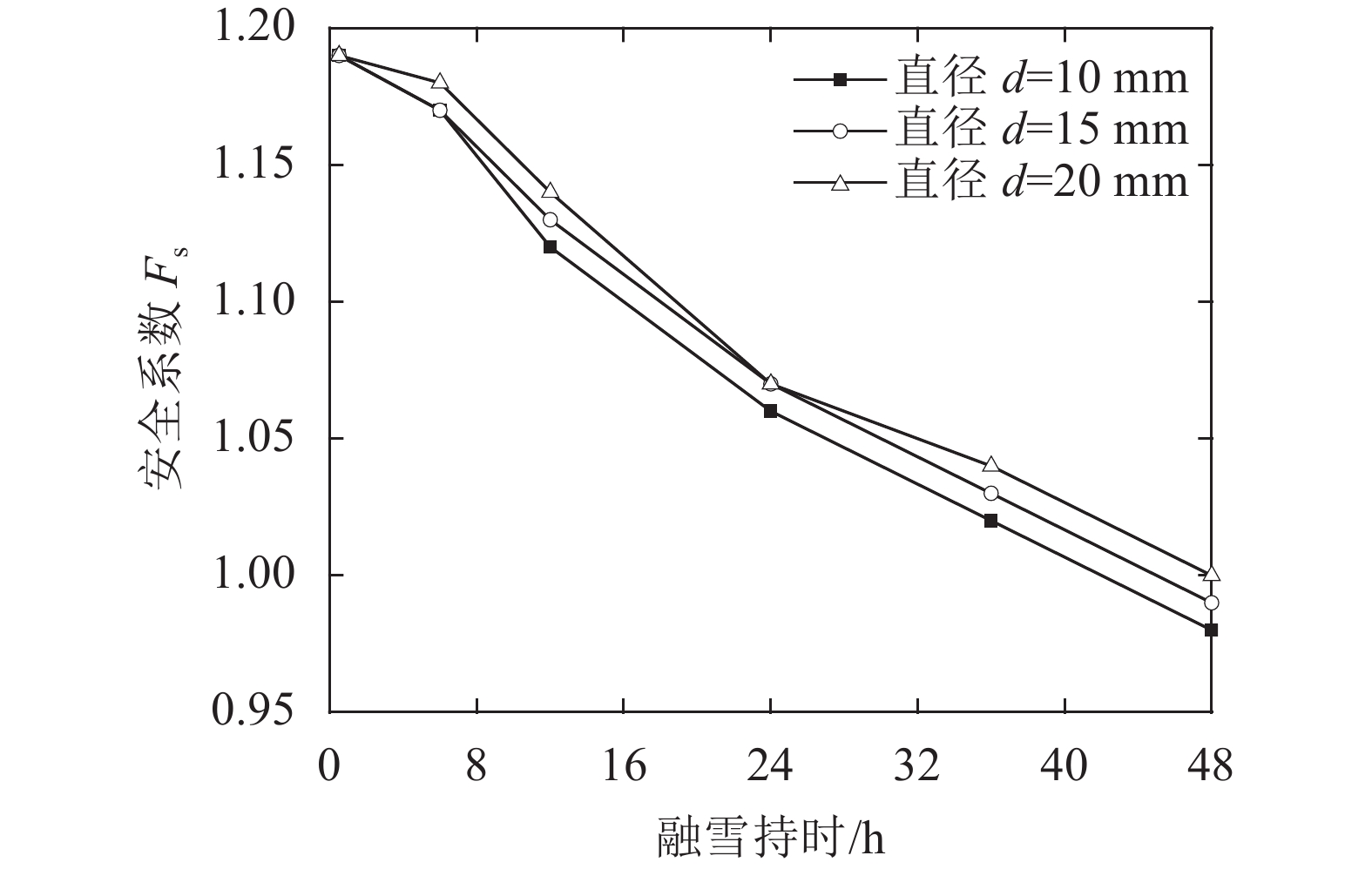 |
| 图17 不同大孔隙直径下边坡安全系数变化 Fig. 17 Relationship between safety factors and diameter of macropore |
由图17可知:随着融雪持时的增长,各工况下的安全系数均出现下降,至融雪结束时(第48 h),安全系数分别下降了14.8%、14.1%、13.4%。这表明增加大孔隙直径,增大了大孔隙域与周围基质域的水分交换量,一定程度上减缓了水流的优先传导作用和孔隙水压力的增长,但影响效果并不明显。
3.2 大孔隙间距的影响 3.2.1 大孔隙间距对边坡水分场的影响分别选取大孔隙的间距s为2.0、1.0、0.5 m这3种工况,其余条件不变,计算3种工况下大孔隙域和基质域内不同深度处含水率随时间的变化过程如图18所示。
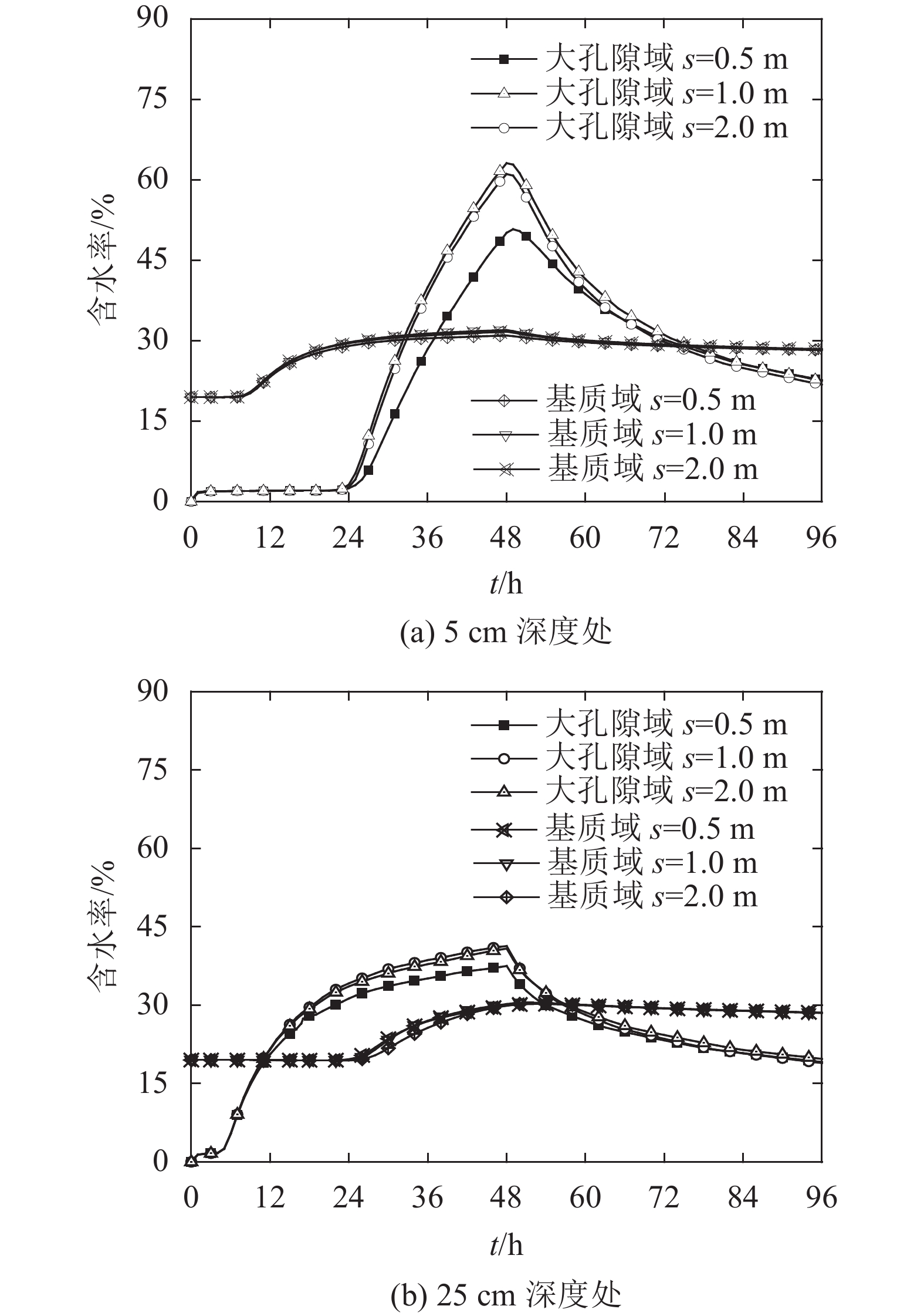 |
| 图18 不同大孔隙间距下各深度含水率变化 Fig. 18 Relationship between water content and distance of macropore |
由图18可知:1)当大孔隙间距由2 m缩小为1.0 m时,相同位置大孔隙内各点及基质域各点的含水率基本保持不变,即此时大孔隙间距对大孔隙、基质域含水率的影响较小;2)当大孔隙间距由1.0 m缩小为0.5 m时,大孔隙对入渗的响应时间出现一定滞后,各点含水率均出现不同程度的下降,降幅随深度的增加而增大,其中25 cm深度处时,大孔隙含水率降幅达10%;基质域内各深度处含水率出现一定程度下降,最大下降幅值为1.03%。这表明大孔隙间距减小,大孔隙间的相互作用加强,在很大程度上导致了大孔隙域、基质域水分传导速率的下降,进而造成了各点含水率不同程度的下降。
3.2.2 大孔隙间距对边坡稳定性的影响分别选取大孔隙间距为2.00、1.50、1.00、0.75、0.50 m这5种工况,其他条件不变,得到不同大孔隙间距下边坡在冰雪消融过程中安全系数的变化如图19所示。
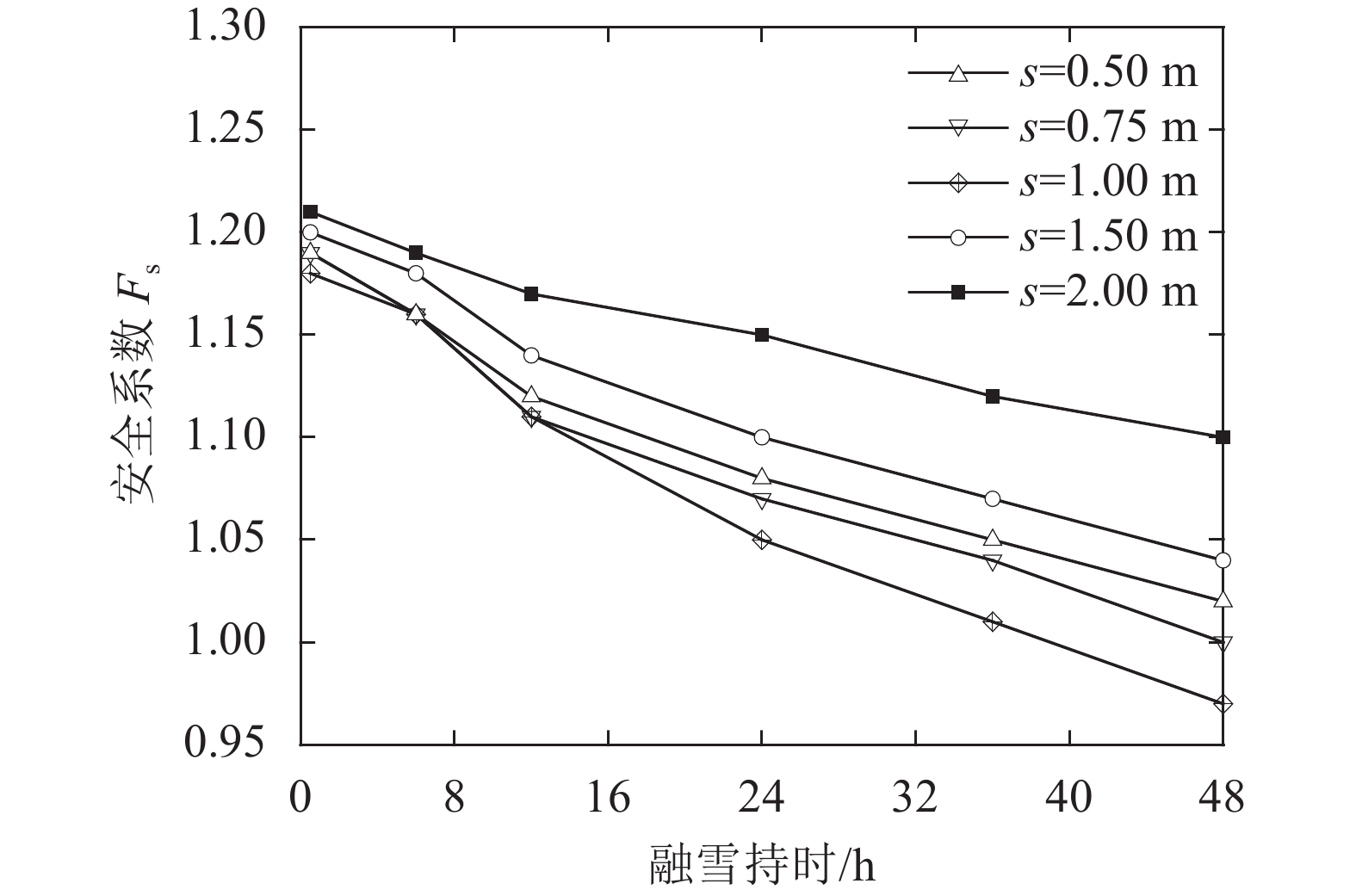 |
| 图19 不同大孔隙间距下边坡安全系数变化 Fig. 19 Relationship between safety factors and distance of macropore |
由图19可知:大孔隙间距由大变小的过程中,边坡安全系数均随融雪持时呈下降趋势,且边坡安全系数降幅随大孔隙间距变大呈先降低后增大的趋势。如大孔隙间距为2、1和0.5 m时,边坡安全系数在融雪持时48 h内分别下降了8.3%、14.7%和11.9%。由此说明,边坡安全系数与大孔隙间距之间存在一个临界间距,即在此间距时,边坡安全系数最低。造成此的原因在于大孔隙间距较大时,大孔隙群的优先流效应无法发挥,对于边坡安全系数的影响不明显;当大孔隙间距较小时,大孔隙间非平衡流相互叠加与干扰,导致了大孔隙对于表层深处孔隙水压力的影响被削弱。
3.3 大孔隙弯曲率的影响 3.3.1 大孔隙弯曲率对边坡水分场的影响实际残积土中的大孔隙分布路径并不一定以竖直方向作为唯一存在形式,大孔隙的分布路径可能存在一定的弯曲,由此对土中不同位置的孔隙水压力变化会产生一定影响。弯曲率是描述大孔隙路径弯曲程度的一个特征参数,是一个不小于1的无量纲参数,一般来说,可通过式(5)定义[15]。大孔隙下端与竖直方向夹角分别为160°、135°、100°,即弯曲率1.03、1.17、1.78这3种工况(图20)对边坡各深度水分场的影响如图21所示,其余条件不变:
| $\tau = \frac{{{L_{\rm e}}}}{L}$ | (5) |
式中:
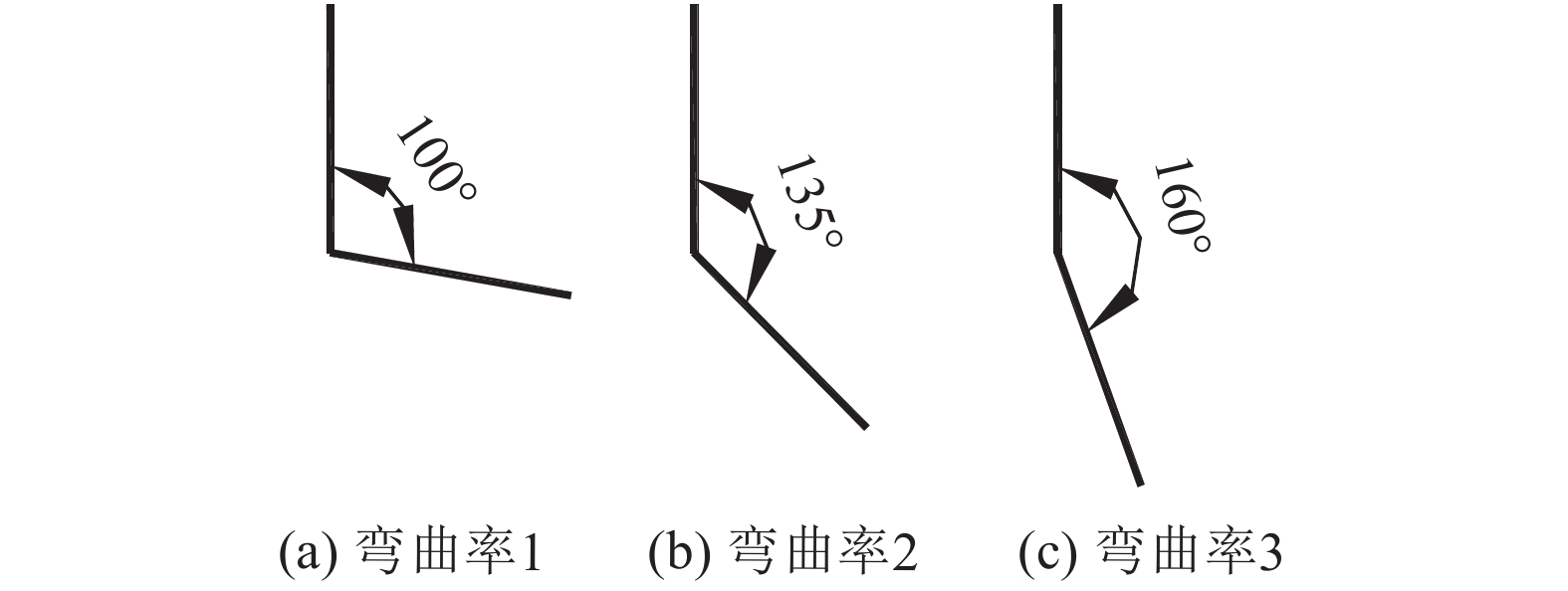 |
| 图20 3种大孔隙弯曲率 Fig. 20 Three types of bending ratio of macropore |
 |
| 图21 不同大孔隙弯曲率下各深度含水率变化 Fig. 21 Relationship between water content and bending ratio of macropore |
由图20可知:当大孔隙弯曲率由1.03增至1.17时,各深度处大孔隙域、基质域含水率变化不明显;当大孔隙弯曲率由1.17增至1.78时,各深度处大孔隙域含水率出现明显升高,且含水率增幅随深度增加越明显,如在25 cm深度处含水率增幅达4.4%,最大增幅仅为0.87%。这说明大孔隙弯曲率的增加对于大孔隙各深度处含水率有一定的影响作用,但对基质域含水率变化基本不产生影响。
3.3.2 大孔隙弯曲率对边坡稳定性的影响分别选取大孔隙弯曲率为1.03、1.17、1.78这3种工况,其他条件不变,可得不同大孔隙弯曲率下边坡在冰雪消融过程中安全系数的变化如图22所示。
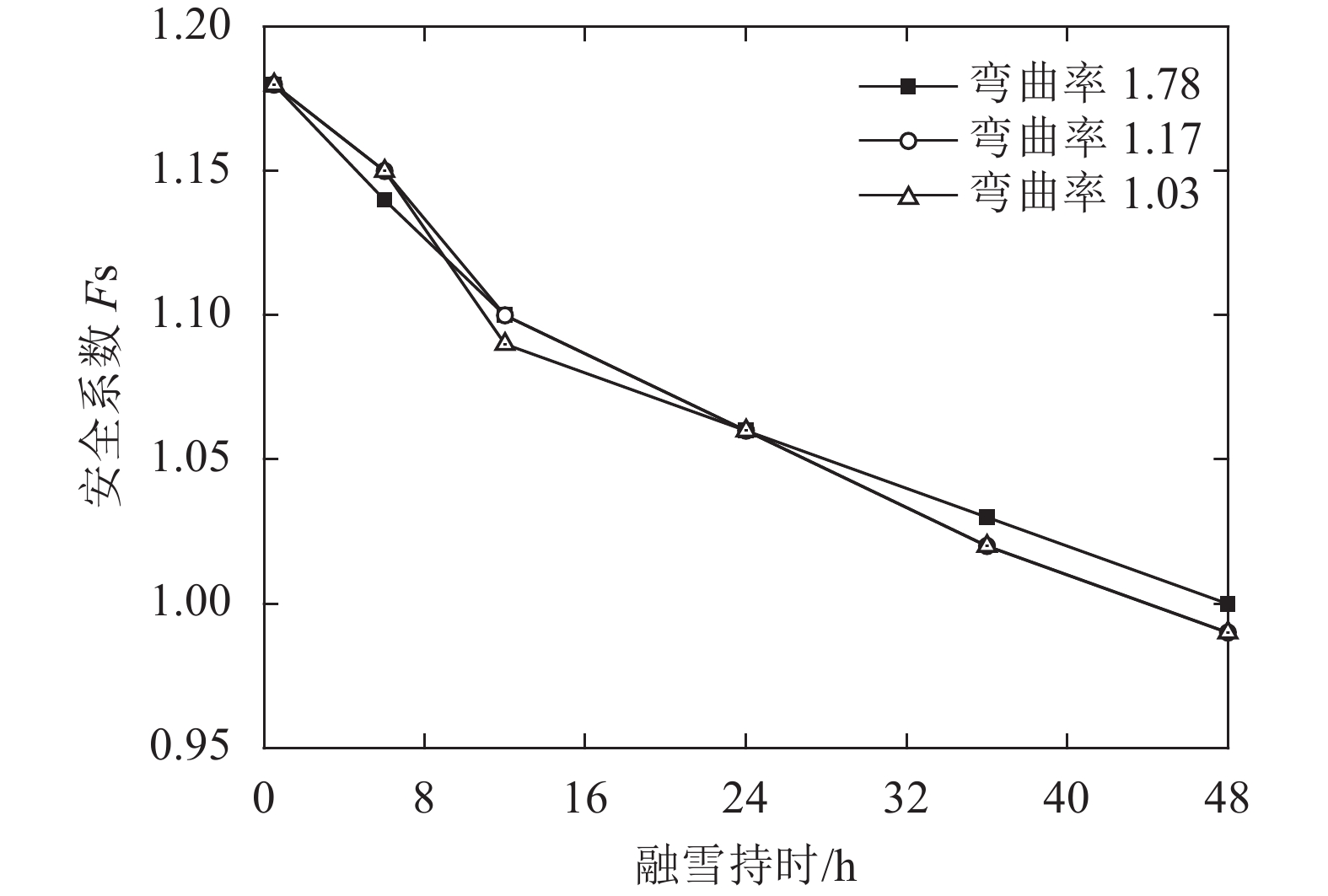 |
| 图22 不同大孔隙弯曲率下边坡安全系数变化 Fig. 22 Relationship between safety factors and bending ratio of macropore |
由图22可知:不同大孔隙弯曲率下,融雪入渗后的残积土边坡安全系数随融雪持时的增加呈现下降趋势,且趋势规律基本一致。如3种大孔隙弯曲率条件下,边坡安全系数随融雪持时的增加分别下降了0.17、0.18、0.18,降幅分别为11.8%、12.3%、12.3%,安全系数最大差值仅为0.01。由此说明,当大孔隙弯曲率发生变化时,其对入渗情况下的边坡安全系数的影响十分微小,可忽略不计。
3.4 大孔隙长度的影响 3.4.1 大孔隙长度对边坡水分场的影响分别选取大孔隙的长度L为0.25、0.50、1.00 m,其余条件不变,计算3种工况下大孔隙域、基质域内不同深度处含水率的变化过程如图23所示。
 |
| 图23 不同大孔隙长度下各深度含水率变化 Fig. 23 Relationship between water content and length of macropore |
由图23可知:1)当大孔隙长度由0.25增大至1.00 m时,25 cm深度处含水率出现了大幅度下降,下降幅值为22.73%;2)当大孔隙长度增大时,各深度处基质域含水率下降幅度不明显,最大差值为1.87%;3)随深度的增大,大孔隙含水率变化对于冰雪消融入渗的响应时间出现滞后。由此说明,当大孔隙长度增大时,大孔隙优先流传递的路径延长,原先的大孔隙底部区域仅发挥优先传导水分的作用,而不再逐渐积累水分,因此在含水率上出现了下降,但大孔隙长度变化对于基质域含水率影响不大。
3.4.2 大孔隙长度对边坡稳定性的影响分别选取大孔隙长度为0.25、0.50、1.00、1.50 m,其余条件不变,计算得到不同大孔隙长度下边坡在融雪过程中安全系数的变化如图24所示。
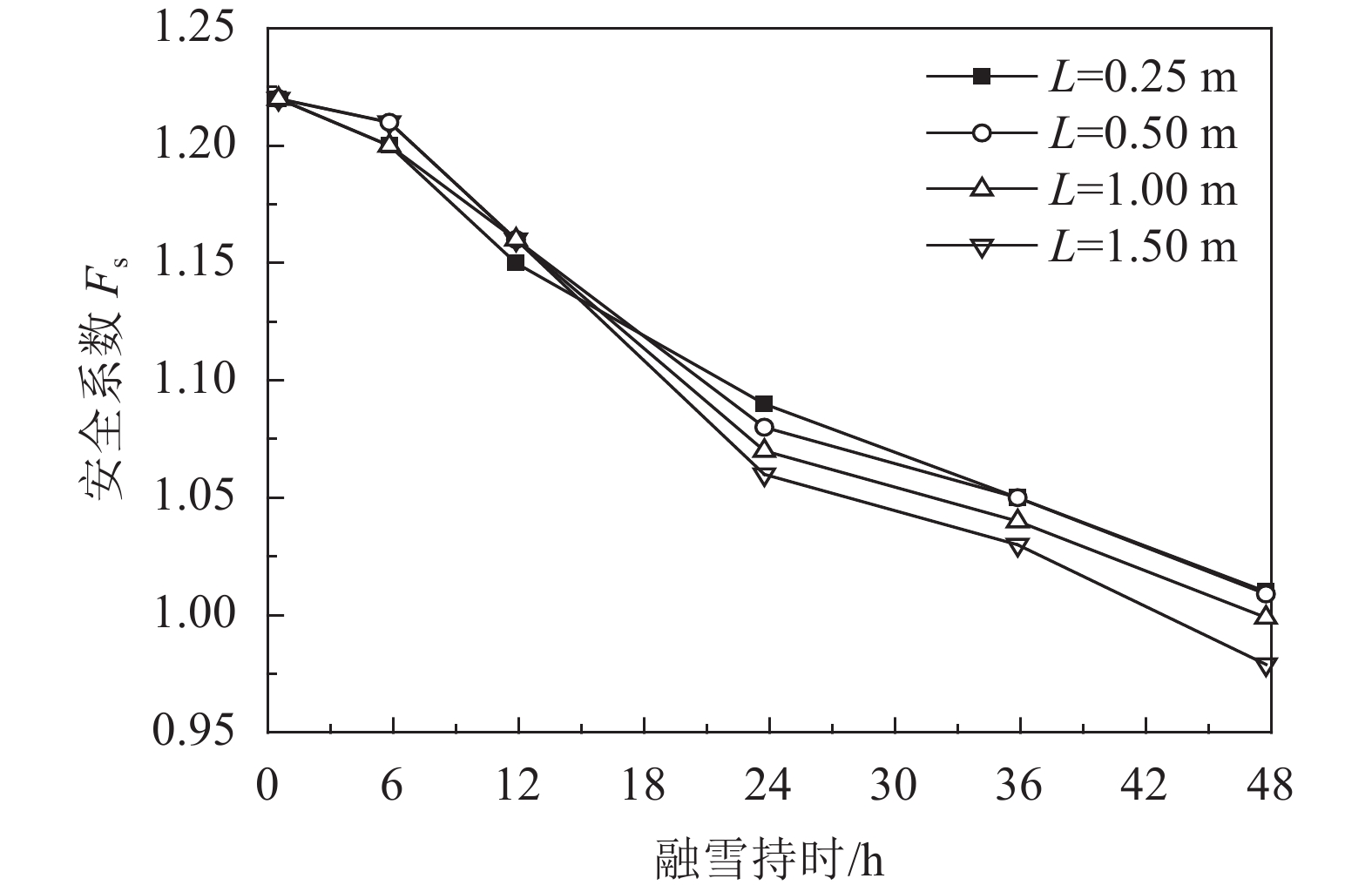 |
| 图24 不同大孔隙长度下边坡安全系数变化 Fig. 24 Relationship between safety factors and length of macropore |
由图24可知:当大孔隙长度为0.25 m时,在整个融雪入渗过程中,能发挥优先渗流的作用,在0~24 h期间安全系数相比于非饱和渗流下降较快,但对于边坡的表层深处孔隙水压力的影响不大,安全系数在整个过程中下降幅度为14.8%;当大孔隙长度继续增加至0.50~1.50 m时,安全系数下降幅度变化不大,最大为0.04。这说明大孔隙长度的增加,延长了水分的传导路径,削弱了大孔隙域内水分的积累效果,对边坡安全系数有一定影响。
4 结 论1)非平衡渗流相比于非饱和渗流对于边坡渗流场与稳定性影响明显更大,采用非平衡流理论可合理解释冰雪消融条件诱发残积土边坡失稳机理。对于短时冻区冰雪消融诱发含大孔隙边坡的失稳问题,应考虑非平衡流的影响,尤其是大孔隙间距与长度,而大孔隙弯曲率的影响可忽略不计。
2)增大大孔隙直径可增大大孔隙域与周围基质域的水分交换量,减缓水流的优先传导作用和孔隙水压力的增长,从而边坡稳定性降低。
3)边坡安全系数降幅随大孔隙间距变大呈现先降低后增大趋势,说明边坡安全系数与大孔隙间距之间存在安全系数最小的临界间距。间距过大导致大孔隙群的优先流效应无法发挥,而间距过小导致大孔隙间非平衡流相互叠加与干扰,削弱大孔隙对于表层深处孔隙水压力的影响。
4)增加大孔隙长度延长了水分的传导路径,原先的大孔隙底部区域,仅发挥优先传导水分的作用,从而削弱大孔隙域内水分的积累效果,同时大孔隙长度对于边坡安全系数有一定影响。
本文尝试引入大孔隙非平衡流理论揭示短时冻区冰雪消融诱发含大孔隙边坡的失稳机理,虽然初步得出一些结论,但仍存在一些问题,如如何准确设置模拟中大孔隙参数(如直径、间距、长度等)问题以贴近实际边坡工程,需进一步研究并予以完善。
| [1] |
徐斅祖,王家澄,张立新.冻土物理学[M].北京:科学出版社,2010.
|
| [2] |
Li Yuanyao, Chai Bo, Miao Haibo. Correlation analysis between geological disasters and extreme ice-snow climate in Southern China[J]. Safety and Environmental Engineering, 2012, 19(6): 22-28. [李远耀, 柴波, 缪海波. 南方极端冰雪气候与地质灾害的关系分析[J]. 安全与环境工程, 2012, 19(6): 22-28.] |
| [3] |
Swanger K M, Marchant D M. Sensitivity of ice-cemented antarctic soils to greenhouse-induced thawing:Are terrestrial archives at risk?[J]. Earth and Planetary Science Letters, 2007, 259(3/4): 347-359. |
| [4] |
Charles H, James S, Michael C. An investigation of periglacial slope stability in relation to soil properties based on physical modelling in the geotechnical centrifuge[J]. Geomorphology, 2008, 93(3/4): 437-459. |
| [5] |
Yin Kunlong. Research survey on Switzerland landslide[J]. The Chinese Journal of Geological Hazard and Control, 1999, 10(4): 104-107. [殷坤龙. 瑞士滑坡及其研究概况[J]. 中国地质灾害与防治学报, 1999, 10(4): 104-107.] |
| [6] |
Wu Weijiang. Promoting effect of seasonal frozen stagnant water slip—A new factor of landslide development[J]. Journal of Glaciology and Geocryology, 1997, 19(4): 359-365. [吴玮江. 季节性冻结滞水促滑效应—滑坡发育的一种新因素[J]. 冰川冻土, 1997, 19(4): 359-365.] |
| [7] |
Zhang Yongxing, Wang Yunbin, Song Xicheng. Stability analysis of bedding rock slope under the condition of extreme ice-snow[J]. Journal of Disaster Prevention and Mitigation Engineering, 2011, 31(4): 351-357. [张永兴, 王韵斌, 宋西成. 极端冰雪条件下的顺层岩质边坡滑移稳定性分析[J]. 防灾减灾工程学报, 2011, 31(4): 351-357.] |
| [8] |
Zhang Lianyong.Stability analysis of rock wedge under the condition of extreme ice-snow disaster[D].Chongqing:Chongqing University,2012 [张连勇.极端冰雪灾害条件下岩质楔形体稳定性分析[D].重庆:重庆大学,2012.]
|
| [9] |
Zheng Changan, Chao Wanli. Analysis of slope stability under the condition of extreme ice-snow[J]. Highway Engineering, 2012, 37(3): 42-44. [郑长安, 巢万里. 极端冰雪条件下边坡稳定性分析[J]. 公路工程, 2012, 37(3): 42-44.] |
| [10] |
Miao Haibo, Yin Kunlong, Xing Linxiao, et al. Evolution analysis of loose accumulation body slope[J]. Rock and Soil Mechanics, 2012, 33(1): 147-153. [缪海波, 殷坤龙, 邢林啸. 极端冰雪灾害条件下松散堆积体边坡演化分析[J]. 岩土力学, 2012, 33(1): 147-153.] |
| [11] |
Cheng Jinhua, Zhang Hongjiang, Shi Yuhu. The effect of preferential flow on seepage and surface runoff in the granite area of the Three Gorges of the Yangtze River[J]. Bulletin of Soil and Water Conservation, 2007, 27(2): 18-23. [程金花, 张洪江, 史玉虎. 长江三峡花岗岩地区优先流对渗流和地表径流的作用[J]. 水土保持通报, 2007, 27(2): 18-23.] |
| [12] |
Gao Zhaoxia, Xu Xuexuan, Zhao Jiaona. Review on macropore flow in soil[J]. Acta Ecologica Sinica, 2014, 34(11): 2801-2811. [高朝侠, 徐学选, 赵娇娜. 土壤大孔隙流研究现状与发展趋势[J]. 生态学报, 2014, 34(11): 2801-2811.] |
| [13] |
Gerke H H V, Genuchten M T. A dual-porosity model for simulating the preferential movement of water and solutes in structured porous media[J]. Water Resources Research, 1993, 29(2): 305-319. DOI:10.1029/92WR02339 |
| [14] |
弗雷德隆德,拉哈尔佐.非饱和土土力学[M].北京:中国建筑工业出版社,1997.
|
| [15] |
Zhang Jiaming.Research on the effects of macropores on rainfall infiltration in vadose zone soils of well vegetated slope[D].Kunming:Kunming University of Science and Technology,2013. [张家明.植被发育斜坡非饱和带土体大孔隙对降雨入渗影响研究[D].昆明:昆明理工大学,2013.]
|
| [16] |
Hai Long, Liang Bing. Stability analysis of soil slope under the condition of rainfall infiltration[J]. Journal of Water Resources and Water Engineering, 2010, 21(4): 46-50. [海龙, 梁冰. 考虑降雨入渗条件的土体边坡稳定性分析[J]. 水资源与水工程学报, 2010, 21(4): 46-50.] |
| [17] |
van Genuchten M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal, 1980, 44(5): 892-898. DOI:10.2136/sssaj1980.03615995004400050002x |
| [18] |
Lin Denghui.Study on macropores infiltration and moisture and heat migrate mechanism in eluvial soil slope in damp-heat areas[D].Fuzhou:Fuzhou University,2013 [林登辉.湿热区残积土边坡大孔隙渗流与水热迁移机理[D].福州:福州大学,2013.]
|
| [19] |
Deng Xiangyu.Research on seepage characteristics and stability of residual soil slope under the condition of ice-snow melting[D] Fuzhou:Fuzhou University,2016 [邓翔宇.冰雪消融条件下残积土边坡渗流特性与稳定性研究[D].福州:福州大学,2016.]
|
| [20] |
Qian Xiaohui, Rong Guan, Huang Kai. Slope seepage calculation and stability analysis under the condition of ice-snow melting[J]. Chinese Journal of Prevention and Control of Geologic Disasters, 2010, 21(4): 27-33. [钱晓慧, 荣冠, 黄凯. 融雪入渗条件下边坡渗流计算及稳定性分析[J]. 中国地质灾害与防治学, 2010, 21(4): 27-33.] |
 2017, Vol. 49
2017, Vol. 49

