液压阻尼器广泛应用于航空、航天、军工及汽车等领域,具有刚度低、阻尼大等特点。为了保护设备安全可靠,一般设置定压活门限制载荷过大。理论上,液压阻尼器模型考虑的实际因素越多计算结果越精确,但是模型越复杂对算法的要求也就越高,而且往往需要很小的计算步长才能达到一定精度,这样将极大地增加计算时间,不便于工程应用。因此,建立准确、简洁的力学模型十分必要,将有利于液压阻尼器的优化设计和性能分析。
目前,Patten、Farjoud等[1–2]对不带定压活门的液压阻尼器建模时均采用常数弹性模量计入油液压缩性的影响。Titurus等[3–4]建模时,油液弹性模量计入了油气混合及结构弹性的影响。也有单独对定压活门进行建模研究,Hayashi等[5]在建立定压活门的动力学模型时,计入了阀口液动力及串油管路阻力的影响,未考虑含气量对油液压缩性的影响,采用的弹性模量也为常量,阀口等效面积简化为关于阀芯位移的一次函数,阀口流量系数为基于实验数据拟合的关于阀芯位移的函数。对于带定压活门的液压阻尼器建模,不同研究考虑的因素不尽相同,Su等[6]建模时没有计入油液压缩性、阀口液动力及串油管路的影响,阀口流量系数为常量。Eyres等[7–8]和Bottasso等[9]所建模型中油液体积弹性模量为常量,阀口流量系数与等效面积的处理同Hayashi等[5]一样,没有计入阀口液动力及串油管路的影响。Bauchau等[10]所建模型中弹性模量为基于实验数据拟合的关于压强的函数,阀口流量系数为常量,阀口等效面积为阀芯位移的二次函数,未计入阀口液动力、串油管路的影响。
现有液压阻尼器模型对油液含气和压缩性、阀口液动力、阀口流量系数和等效面积、串油管路等因素的计算不尽相同,给工程应用造成一定混乱。液压阻尼器主要功能是提供阻尼消耗能量,定压活门的作用是限制载荷过大。因此,作者主要从耗能效果和阻尼力两方面对以上因素进行分析,为带定压活门的液压阻尼器建立简洁准确的力学模型。
1 液压阻尼器模型液压阻尼器定压活门内置和外接时如图1所示。图1中,P1、P2分别为液压缸右腔和左腔的压强,Qd、Qv分别为流经活塞孔和定压活门的流量,Pv1、Pv2分别为定压活门右侧和左侧的压强,Q1、Q2分别为液压缸右腔流入管路和管路流入液压缸左腔的流量。
 |
| 图1 带定压活门的液压阻尼器 Fig. 1 Hydraulic damper with pressure relief valve |
定压活门内置时,一般活塞运动引起阀芯的惯性力
| $\left\{ \begin{split}& m\ddot x + c\dot x + kx = {A_{\rm s}}\left| {{P_{\rm L}}} \right| \cdot \\& \qquad (1 - 4{C_{{\rm q}0}}\displaystyle\frac{{\gamma x}}{{1 + \gamma x}}\frac{x}{d}\sin \,\, 2\alpha ) - {F_0},\\& {Q_{\rm v}}{\rm{ = }}{C_{{\rm q}0}}\displaystyle\frac{{\gamma x}}{{1 + \gamma x}}\text{π} (d - x\tan \,\, \alpha ) \cdot \\& \qquad x{\rm{sin}}\; \alpha {\mathop{\rm sgn}} ({P_{\rm L}})\sqrt {\displaystyle\frac{{2\left| {{P_{\rm L}}} \right|}}{\rho }}, \\& \frac{V}{{4\beta }}{{\dot P}_{\rm L}} = {A_{\rm t}}\dot s - {C_0}{A_{\rm d}}{\mathop{\rm sgn}} ({P_{\rm L}})\sqrt {\displaystyle\frac{{2\left| {{P_{\rm L}}} \right|}}{\rho }} - {Q_{\rm v}}\end{split} \right.$ | (1) |
式中,m为阀芯质量,c、k分别为定压活门阻尼和刚度,x为阀芯相对阀座的位移,As为阀芯受压面积,PL=P1–P2为活塞负载压强,Cq0=0.8为阀口常流量系数,
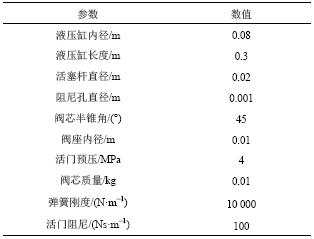
液压阻尼器的主要功能是提供阻尼、消耗能量,定压活门的作用是限制载荷过大,防止结构破坏。因此,在分析各种因素的影响时,主要从耗能效果、阻尼力两方面考虑,所依据的指标为等效阻尼Ce、阻尼力峰值Fa。在计算等效阻尼时采用简谐激励,激励频率为1 Hz,其他主要参数如表1所示。
| 表1 液压阻尼器参数 Tab. 1 Parameters of a hydraulic damper |
 |
2.1 油液含气和压缩性影响
油液含气是通过改变油液压缩性影响液压阻尼器的力学性能,衡量压缩性的指标为油液体积弹性模量,计算公式[11]为:
| $\beta = {\left[ {\frac{\eta }{{nP}}{{\left(\frac{{{P_{{\rm{atm}}}}}}{P}\right)}^{\frac{1}{n}}} + \frac{{1 - \eta }}{{{\beta _{\rm e}}}}{{\rm e}^{\frac{{{P_{{\rm{atm}}}} - P}}{{{\beta _{\rm e}}}}}}} \right]^{ - 1}}$ | (2) |
式中,η为含气体积百分比,n=1.1~1.4为气体多变指数,P为油液压强,Patm=0.101 MPa为大气压强,
采用式(2)对不同压强下的体积弹性模量进行计算,随含气量的变化如图2所示。
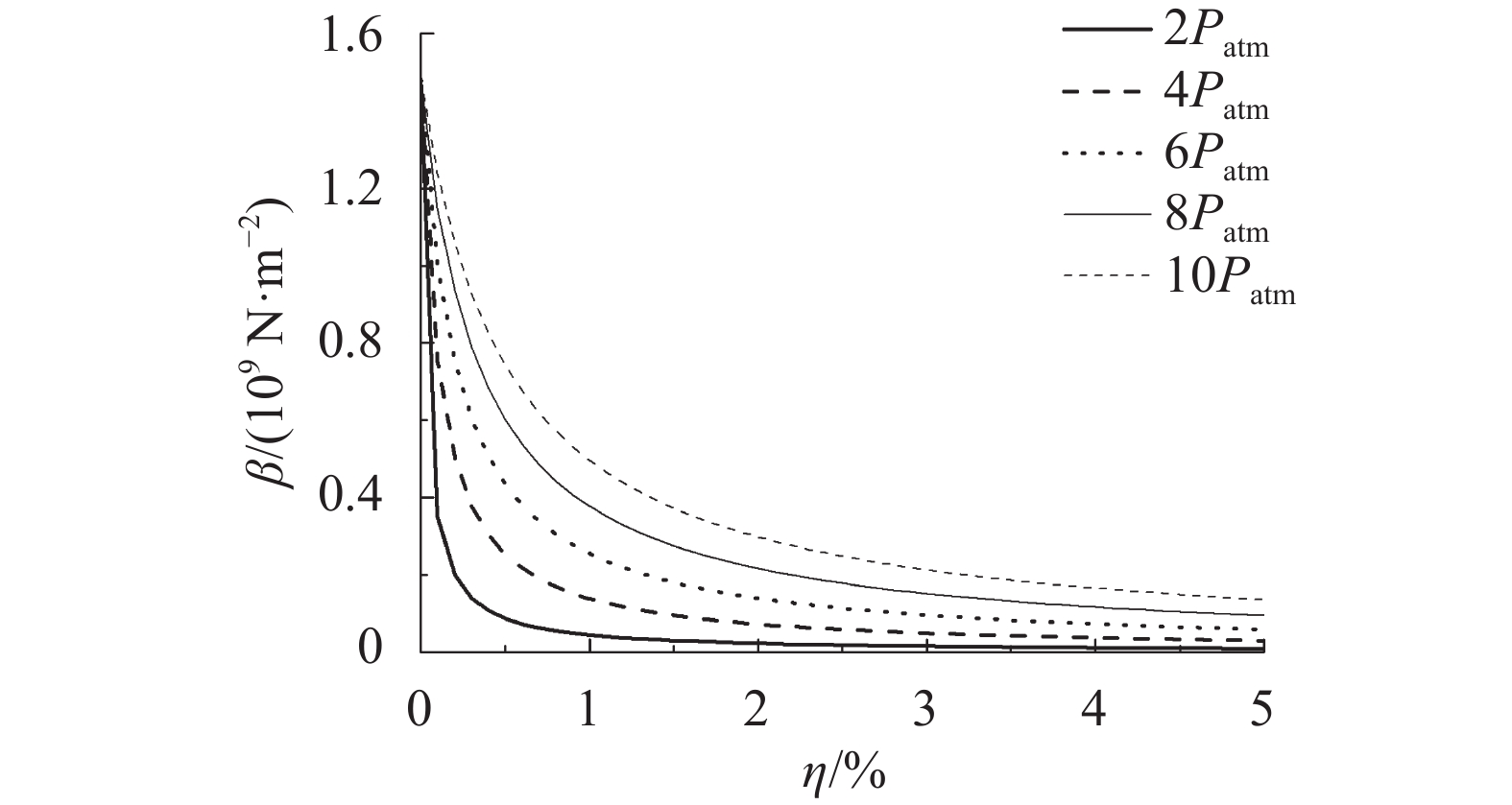 |
| 图2 不同压强时油液弹性模量随含气量变化曲线 Fig. 2 Changing curves of oil elastic modulus with air percentages at different pressure |
由图2可知:油液含气小于1%时,其弹性模量随含气量的增加急速下降;压强增加时,该下降趋势有所减缓但仍降低不少。因此,尽管阻尼器油液中含气量非常少,但仍有可能对其力学性能产生较大影响。
取不同弹性模量时,等效阻尼及阻尼力峰值随激励幅值的变化情况如图3所示。
 |
| 图3 弹性模量对Ce和Fa的影响 Fig. 3 Influence of elastic modulus on Ce and Fa |
由图3可知,等效阻尼随弹性模量的减小而减小,而定压活门开启后随着激励幅值的增加弹性模量对等效阻尼的影响逐渐减小。定压活门开启前弹性模量越小阻尼力峰值也越小,且活门开启需要的激励幅值越大;定压活门开启后阻尼力峰值基本不受弹性模量的影响。因此,在建模时必须考虑由油液含气引起弹性模量变化的影响。
2.2 阀口液动力影响若不考虑阀口液动力的影响,液压阻尼器模型为:
| $\left\{ \begin{aligned}& m\ddot x + c\dot x + kx = {A_{\rm s}}\left| {{P_{\rm L}}} \right| - {F_0},\\& {Q_{\rm v}}{\rm{ = }}{C_{\rm q0}}\displaystyle\frac{{\gamma x}}{{1 + \gamma x}}\text{π} (d - x\tan \,\, \alpha ) \cdot \\& \quad\quad x{\rm{sin}}\,\, \alpha {\mathop{\rm sgn}} ({P_L})\sqrt {\displaystyle\frac{{2\left| {{P_{\rm L}}} \right|}}{\rho }}, \\& \displaystyle\frac{V}{{4\beta }}{{\dot P}_{\rm L}} = {A_{\rm t}}\dot s - {C_0}{A_{\rm d}}{\mathop{\rm sgn}} ({P_{\rm L}})\sqrt {\displaystyle\frac{{2\left| {{P_{\rm L}}} \right|}}{\rho }} - {Q_{\rm v}}\end{aligned} \right.$ | (3) |
忽略阀口液动力后,等效阻尼及阻尼力峰值随激励幅值的变化情况如图4所示。
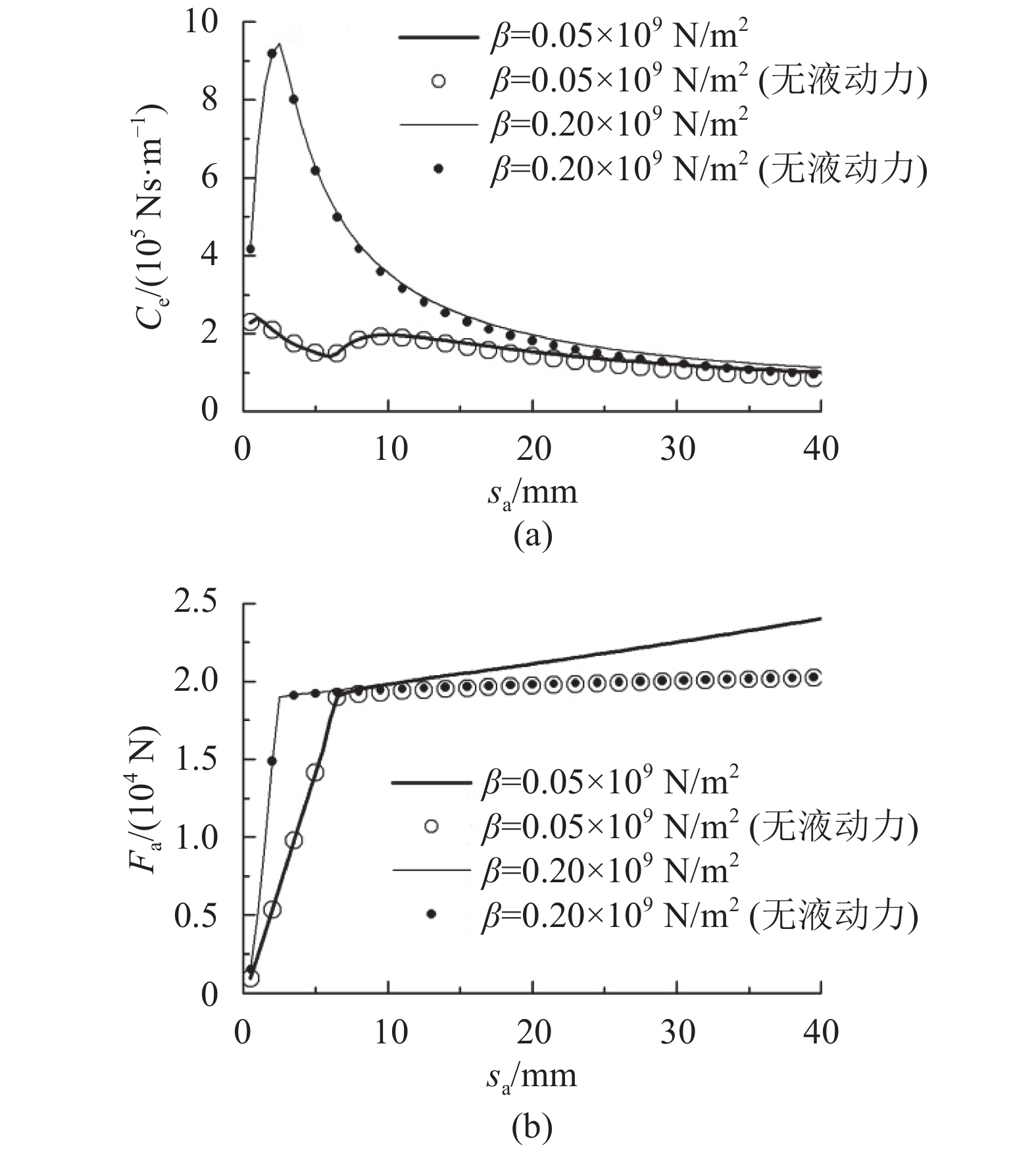 |
| 图4 液动力对Ce和Fa的影响 Fig. 4 Influence of dynamic flow force on Ce and Fa |
由于阀口液动力在活门开启后才起作用,因此活门开启前阻尼力峰值和等效阻尼均不受影响。由式(1)可知,活门开启后,液动力对阀芯运动产生负的作用力,会减小阀芯位移,从而增加活塞负载,且随着阀芯位移的增加该作用会越来越大。由图4可知,液动力对等效阻尼的影响较小,说明在整个激励周期中由液动力引起负载做功的差异不大。但是,活门开启后,忽略液动力后阻尼力峰值减小,且随着激励幅值的增加两种计算结果差值越大。因此,在建模时不能忽略阀口液动力的影响。
2.3 阀口流量系数和等效面积影响若阀口流量系数为常量,阀口等效面积简化成阀芯位移的一次函数,液压阻尼器模型为:
| $\left\{ \begin{aligned}& m\ddot x + c\dot x + kx = {A_{\rm s}}\left| {{P_{\rm L}}} \right| \cdot \\& \quad \quad (1 - 4{C_{\rm q0}}\displaystyle\frac{x}{d}\sin \,\, n\,\,2\alpha ) - {F_0}, \\& {Q_{\rm v}}{\rm{ = }}{C_{\rm q0}}\text{π} dx{\rm{sin}}\,\,\,\, \alpha {\mathop{\rm sgn}} ({P_{\rm L}})\sqrt {\displaystyle\frac{{2\left| {{P_{\rm L}}} \right|}}{\rho }}, \\& \displaystyle\frac{V}{{4\beta }}{{\dot P}_{\rm L}} = {A_{\rm t}}\dot s - {C_0}{A_{\rm d}}{\mathop{\rm sgn}} ({P_{\rm L}})\sqrt {\displaystyle\frac{{2\left| {{P_{\rm L}}} \right|}}{\rho }} - {Q_{\rm v}}\end{aligned} \right.$ | (4) |
阀口流量系数和等效面积简化后,等效阻尼和阻尼力峰值随激励幅值的变化情况如图5所示。
 |
| 图5 流量系数和等效面积对Ce和Fa的影响 Fig. 5 Influence of discharge coefficient and equivalent area on Ce and Fa |
由图5可知,将阀口流量系数和等效面积进行简化处理对等效阻尼和阻尼力峰值基本没有影响。因此,为简化模型,提高计算效率,阀口流量系数可取常量,阀口等效面积也可简化成阀芯位移的一次函数。
2.4 串油管路阻力和管路油液压缩性影响如果定压活门外接,则还需考虑串油管路阻力和管路油液压缩性的影响,串油管路阻力用Lumped Parameter模型[12]计算,液压阻尼器模型为:
| $\left\{ \begin{aligned}& m\ddot x + c\dot x + kx = {A_{\rm s}}\left| {{P_{\rm vL}}} \right| \cdot (1 - 4{C_{\rm q0}}\displaystyle\frac{x}{d}\sin 2\alpha ) - {F_0},\\& {Q_{\rm v}}{\rm{ = }}{C_{\rm q0}}\text{π} dx{\rm{sin}}\;\alpha {\mathop{\rm sgn}} ({P_{\rm v}}_{\rm L})\sqrt {\displaystyle\frac{{2\left| {{P_{\rm v}}_{\rm L}} \right|}}{\rho }}, \\& \displaystyle\frac{{{A_{\rm l}}l}}{{2\beta }}{{\dot P}_{{\rm vL}}} = {Q_{\rm L}} - {Q_{\rm v}},\\& \displaystyle\frac{{2\rho l}}{{{A_{\rm l}}}}{{\dot Q}_{\rm L}} = {P_{\rm L}} - {P_{\rm vL}}\\& \displaystyle\frac{V}{{4\beta }}{{\dot P}_{\rm L}} = {A_{\rm t}}\dot s - {C_0}{A_{\rm d}}{\mathop{\rm sgn}} ({P_{\rm L}})\sqrt {\displaystyle\frac{{2\left| {{P_{\rm L}}} \right|}}{\rho }} - {Q_{\rm L}}\end{aligned} \right.\!\!$ | (5) |
式中,PvL=Pv1–Pv2为阀芯负载压强,
不同管路时,等效阻尼和阻尼力峰值随激励幅值的变化情况如图6所示。
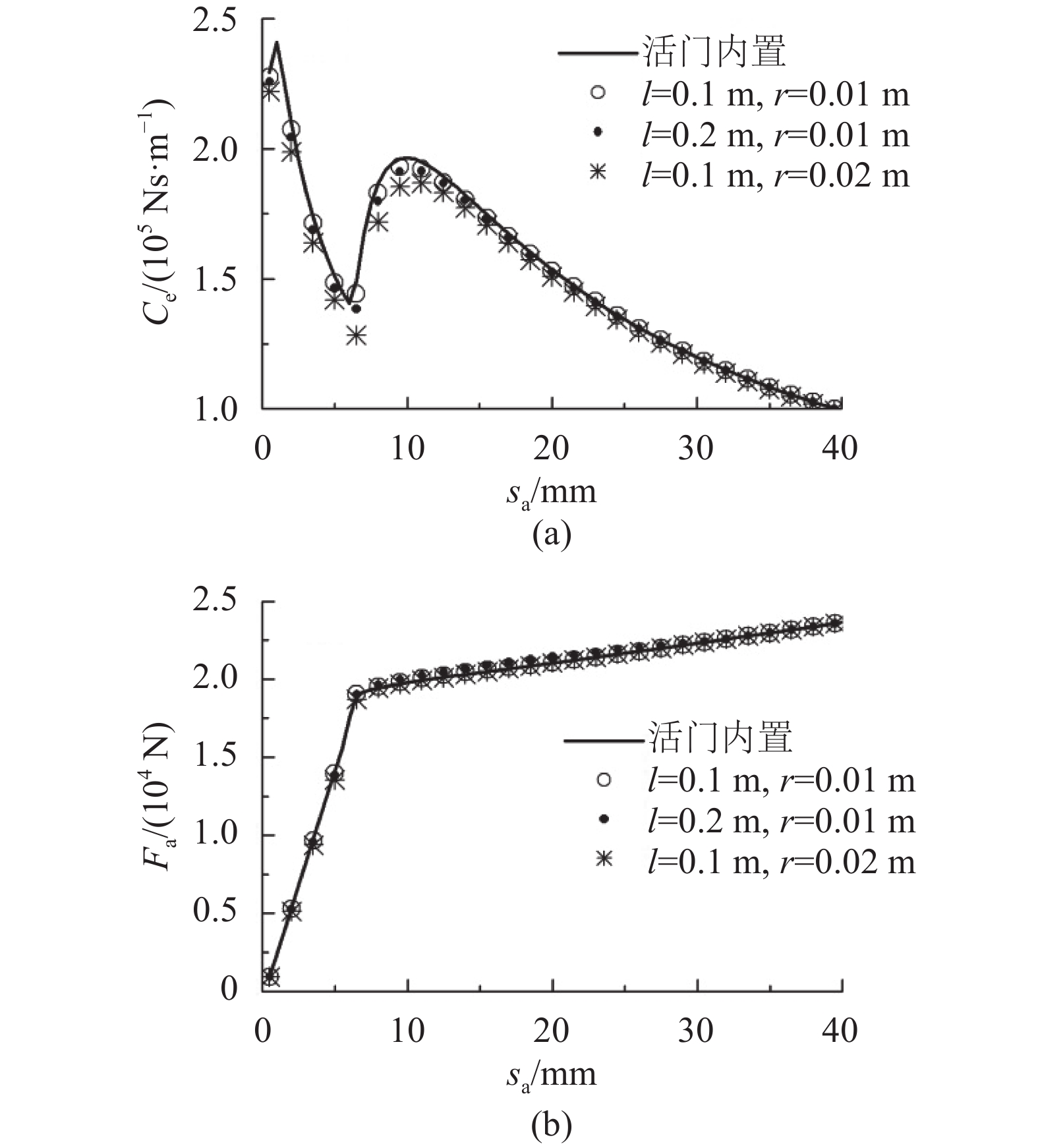 |
| 图6 串油管路对Ce和Fa的影响 Fig. 6 Influence of string pipeline on Ce and Fa |
由式(5)可知,串油管路阻力的影响取决于l/Al,而管路油液压缩性的影响取决于All。串油管路阻力会增加活塞负载,而管路油液压缩性会减小活塞负载,增加管长会同时增加管路阻力和油液压缩性,而增加管路内径则使管路阻力减小而油液压缩性增加。但是由图6可知,管路长度和内径的改变对等效阻尼的影响很小,而对阻尼力峰值基本没有影响。因此,可忽略串油管路阻力和管路油液压缩性的影响,将活门外接时的液压阻尼器模型与内置时统一,即如式(4)所示。
由于油液含气对油液弹性模量的影响较大,需要将表征油液含气对弹性模量影响的式(2)引入液压阻尼器模型式(4)中,得到计入含气量对油液压缩性影响的液压阻尼器模型为:
| $\left\{ \begin{aligned}& m\ddot x + c\dot x + kx = {A_{\rm s}}\left| {{P_{\rm L}}} \right| \cdot (1 - 4{C_{\rm q0}} \displaystyle \frac{x}{d}\sin 2\alpha ) - {F_0},\\& {Q_{\rm v}}{\rm{ = }}{C_{\rm q0}}\text{π} dx{\rm{sin}}\;\alpha {\mathop{\rm sgn}} ({P_{\rm L}})\sqrt {\displaystyle\frac{{2\left| {{P_{\rm L}}} \right|}}{\rho }}, \\& {( - 1)^i}\displaystyle\frac{{{V_i}}}{{{\beta _i}}}{{\dot P}_i} = - {A_t}\dot s +{C_0}{A_d}{\mathop{\rm sgn}} ({P_{\rm L}})\sqrt {\displaystyle\frac{{2\left| {{P_{\rm L}}} \right|}}{\rho }} + {Q_{\rm v}}, \\& {\beta _i} = {\left[ {\displaystyle\frac{\eta }{{n{P_i}}}{{\left(\frac{{{P_{{\rm{atm}}}}}}{{{P_i}}}\right)}^{\frac{1}{n}}} + \frac{{1 - \eta }}{{{\beta _{\rm e}}}}{{\rm e}^{\frac{{{P_{{\rm{atm}}}} - {P_i}}}{{{\beta _{\rm e}}}}}}} \right]^{ - 1}}\end{aligned} \right.$ | (6) |
式中,i=1、2,V1、V2分别为液压缸右腔和左腔的容积,
以某型液压阻尼器为例,分别对激励幅值为0.001、0.009和0.026 m共3种情况下的等效阻尼和阻尼力峰值进行计算,并与实数据对比。等效阻尼误差分别为–9.994 5%、0.672 4%和–2.757 2%,阻尼力峰值误差分别为–0.457 4%、1.973 3%和–4.074 9%。在3种幅值的激励下,等效阻尼和阻尼力峰值的理论计算结果与实验值误差最大不超过10%,验证了所建液压阻尼器力学模型的准确性。
3 结 论通过分析油液含气和压缩性、阀口液动力、阀口流量系数和等效面积、串油管路阻力和管路油液压缩性对带定压活门的液压阻尼器模型计算结果的影响,可得结论:
1)油液含气对油液压缩性的影响很大,而油液压缩性对等效阻尼和阻尼力峰值的影响都很大,建模时应考油液含气对油液压缩性的影响;
2)阀口液动力对活门开启后的阻尼力峰值影响很大,建模时不可忽略;
3)阀口流量系数采用常量且等效面积简化成阀芯位移一次函数后对等效阻尼和阻尼力峰值基本没有影响,建模时可对以上两个因素简化;
4)串油管路阻力和管路油液压缩性对阻尼力峰值基本没有影响,对等效阻尼的影响也很小,建模时可忽略串油管路的影响。
| [1] |
Patten W N, Sack R L, He Q W. Controlled semiactive hydraulic vibration absorber for bridges[J]. Journal of Structural Engineering, 1996, 122(2): 187-192. DOI:10.1061/(ASCE)0733-9445(1996)122:2(187) |
| [2] |
Farjoud A, Ahmandian M, Craft M. Nonlinear modeling and experimental characterization of hydraulic dampers:Effects of shim stack and orifice parameters on damper performance[J]. Nonlinear Dynamics, 2011, 67(2): 1437-1456. |
| [3] |
Titurus B, Bois J D, Lieven N. A method for the identification of hydraulic damper characteristics from steady velocity inputs[J]. Mechanical Systems and Signal Proceesing, 2010, 24(8): 2868-2887. DOI:10.1016/j.ymssp.2010.05.021 |
| [4] |
Titurus B, Bois J D, Lieven N. Modeling and testing of a semiactive hydraulic damper in periodic working regimes[J]. AIAA Journal, 2012, 50(4): 844-854. DOI:10.2514/1.J051152 |
| [5] |
Hayashi S, Hayase T, Kurahashi T. Chaos in a hydraulic control valve[J]. Journal of Fluids and Structures, 1997, 11(6): 693-716. DOI:10.1006/jfls.1997.0096 |
| [6] |
Su H, Rakheja S R, Sankar T S. Vibration and shock isolation performance of a pressure-limited hydraulic damper[J]. Mechanical Systems and Signal Proceesing, 1989, 3(1): 71-86. DOI:10.1016/0888-3270(89)90023-X |
| [7] |
Eyres R D, Piroinen P T, Champneys A R. Grazing bifurcations and chaos in the dynamics of a hydraulic damper with relief valves[J]. Nonlinear Dynamics, 2004, 4(4): 1075-1106. |
| [8] |
Eyres R D, Champneys A R, Lieven N. Modeling and dynamic response of a damper with relief valve[J]. Nonlinear Dynamics, 2005, 40: 119-147. DOI:10.1007/s11071-005-4144-6 |
| [9] |
Bottasso C L, Cacciola S, Croce A. Load reduction in lead-lag dampers by speed-scheduled aperture and modulated control of a by-pass valve[J]. Journal of American Helicopter Society, 2012, 57(2): 16-28. |
| [10] |
Bauchau O A, Liu H Y. On the modeling of hydraulic components in rotorcraft systems[J]. Journal of American Helicopter Society, 2006, 51(2): 175-184. DOI:10.4050/JAHS.51.175 |
| [11] |
贺正辉.液压流体力学[M].太原:太原工学院出版社,1980:153–156.
|
| [12] |
苏尔皇.液压流体力学[M].北京:国防工业出版社,1979:154–155.
|
 2017, Vol. 49
2017, Vol. 49

