自由曲面所表达的产品外观精美,形状可控,具有优良的空气动力学、流体动力学与热力学等特性,使其在航空航天、造船、汽车、能源、国防等要求特殊的行业产品中得到了广泛的应用[1]。中国在自由曲面自动化磨抛技术方面的研究相对滞后,仍处于手工磨抛自由曲面工件型面阶段,效率低、劳动强度大,工件磨抛质量往往取决于工人的加工经验[2],产品可靠性与一致性差,故人工磨抛的方法已无法满足航空、造船等领域的加工需求[3]。因此,寻求一种高效的复杂曲面加工方法成为数控加工领域的研究热点。在自由曲面的数控加工过程中,刀具轨迹规划方法的优劣直接影响其加工精度和加工效率[4]。
在自由曲面砂带磨削加工领域,通过优化接触轮的姿态实现加工行宽的最大化[5],可有效提高加工效率。目前,通过优化加工行距和加工姿态以提高加工效率的理论研究中:贺英等[6]针对等参数轨迹规划中参数间隔固定的相邻两条参数线刀轨在空间上不等距的问题,提出了一种宽行加工等参数线刀轨的精确搭接方法,并通过仿真实验对比验证了其有效性。杨建华等[7]借用二阶泰勒逼近方法计算整条切削轨迹的切削带宽,使原切削带宽提高了26.5%。但上述加工方法都需要大量计算且均以铣削加工为研究对象。目前,在砂带磨抛加工中常用的轨迹规划方法有等参数法、等残高轨迹生成算法等。等参数法刀具路径轨迹较为简单,但其受弓高误差、残余高度及曲面曲率影响,刀具路径轨迹参数选择较为保守,存在冗余刀具路径轨迹。尽管等残余高度法在理论上可以产生最优的刀具路径轨迹,但其相邻刀位轨迹间最大步距都是假设在一个平面内计算的,即相邻刀具路径轨迹的切矢量方向平行,而实际上并非如此;并且该方法对于曲率变化大的曲面易导致步距计算出现较大偏差。由于自由曲面的不规则性,其曲率不断变化,磨削加工时加工行距与步距的选择尤为重要。另外,若磨头尺寸选择不当,则会对加工效率与加工精度产生直接影响。因此选择合理的接触轮尺寸对于自由曲面砂带磨削加工非常重要。目前的选择方法有经验选择法和曲率分析选择法[8],前者选择刀具尺寸比较保守,加工效率的不确定性高,且需要反复调试选择;后者根据曲面曲率分析结果选择最大刀具尺寸,比经验选择法更加科学,但受限于曲面离散精度,在牺牲计算时间的基础上保全计算精度。
针对现有自由曲面加工的轨迹规划中存在的问题与不足,作者通过遗传算法与加工精度控制相结合的方法优选出适宜曲面加工的接触轮尺寸和磨削加工参数,并基于该参数和位姿优化提出了一种适用于磨抛加工的轨迹规划方法。
1 基于遗传算法的接触轮最佳尺寸的优选方法 1.1 接触轮尺寸优选标准与求解公式图1为砂带磨削加工的示意图。图1(a)中,自由曲面上的主曲率决定了曲面主曲率半径,加工自由曲面时,尤其是加工凹面区域时,如果接触轮半径大于磨削点处的最小曲率半径,则会发生局部的曲率干涉从而影响加工质量与加工精度,如图1(b)所示。为了避免曲率干涉必须确保接触轮半径小于曲面的最小主曲率半径,设ρmax为曲面最大主曲率,则接触轮半径R的值应小于1/ρmax的值。
图2为自由曲面常见航发叶片的两种磨削方式。其中,横向行距法与曲面的接触面大,磨削效率高,易产生沿叶片长度方向的波纹;纵向行距法的接触轮与曲面间的接触面小,加工精度高,加工效率低。针对目前自由曲面数控加工效率低的难题,结合叶片型面横向、纵向的磨削加工方法的缺点,作者提出了一种根据误差精度控制原则选取接触轮尺寸与加工参数并通过与图2(a)所示的横向加工相结合的方式使加工曲面满足加工精度的同时进一步提高加工效率的技术思路。
如图1(c)所示,AD为接触轮宽度,设其为W,磨削点在接触轮轴向方向上的曲率半径为
| $\varepsilon \le h \le {R_{\rm{c}}} - \sqrt {{R_{\rm{c}}}^2 - {{(W/2)}^2}} $ | (1) |
为避免加工中接触轮与曲面的间隙大于预期的加工允差,设该曲面所有磨削点与接触轮轴向方向的最小曲率半径为
| $W \le 2\sqrt {2\varepsilon \cdot {R_{\rm{c}}}_{\min } - {\varepsilon ^2}} $ | (2) |
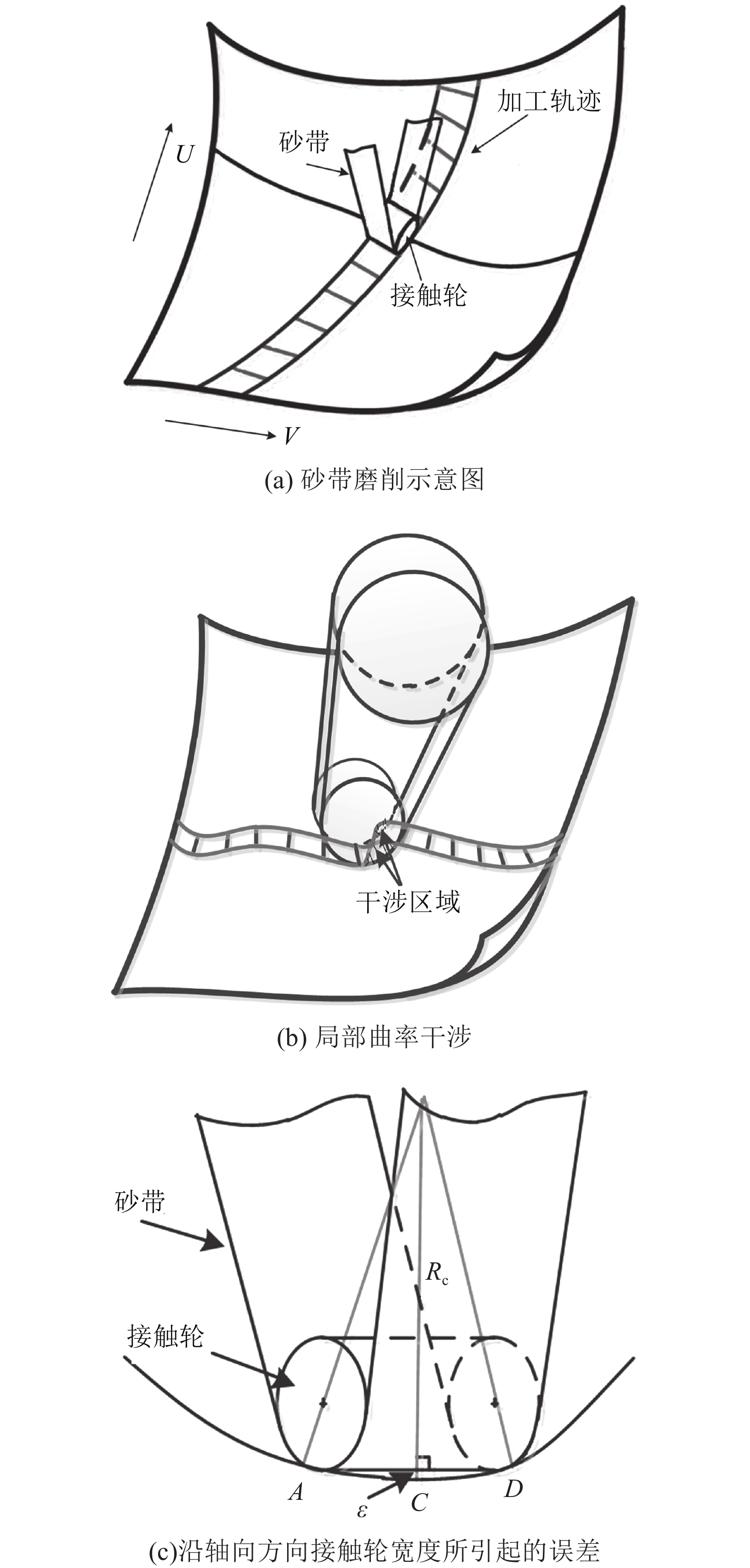 |
| 图1 砂带磨削加工示意图 Fig. 1 Schematic diagram of abrasive belt grinding |
1.2 遗传算法求取曲面最大、最小主曲率
由式(2)可知,接触轮尺寸参数的求解问题可转化为在自由曲面中寻找最大主曲率和所有磨削点在接触轮轴向方向上的最大主曲率。为实现横向宽行磨削加工中接触轮在曲面间的加工行宽的最大化,接触轮轴向应始终沿着磨削点的第一主曲率方向[9],所以只需求取自由曲面中最大主曲率和第一主曲率方向上的最大主曲率。如何快速且准确不遗漏地求取刀位点中的主曲率参数是一个在典型群体中寻找最优解的问题。基于遗传算法在群体寻优方面的优势,考虑到自由曲面参数中u、v这两个参数的特性,作者提出了基于双倍体基因的遗传算法求解自由曲面最大主曲率及第一主曲率方向上最大主曲率的新算法。
假设自由曲面函数为
| $S\!\left( {u,v} \right) = \left[\!\!\! {\begin{array}{*{20}{c}}{x\left( {u,v} \right)}\\{y\left( {u,v} \right)}\\{\textit{z}\left( {u,v} \right)}\end{array}} \!\!\! \right]\text{,}u,v \in \left[ {0,1} \right]$ | (3) |
式中:
| ${k_n} = \frac{{L{d_u}^2 + 2M{d_u}{d_v} + N{d_v}^2}}{{E{d_u}^2 + 2F{d_u}{d_v} + G{d_v}^2}}$ | (4) |
式中:
| $\mathit{\boldsymbol{n}} = \frac{{{\mathit{\boldsymbol{S}}_u} \times {\mathit{\boldsymbol{S}}_v}}}{{|{\mathit{\boldsymbol{S}}_u} \times {\mathit{\boldsymbol{S}}_v}|}}$ | (5) |
自由曲面上对应该点主曲率是法曲率的最大值和最小值,根据高斯曲率和平均曲率可以求取最大、最小主曲率:
| ${k_{1,2}} = H \pm \sqrt {{H^2} - K} $ | (6) |
式中,H与K分别为该点的平均曲率和高斯曲率。
由上述求解公式可知,主曲率k1是参数u和v的函数,求取时需要同时考虑。采用二进制编码方式对u、v进行编码,共同组成种群中的一个个体。由于应用遗传算法在自由曲面中求解最大主曲率及第一主曲率方向上的最大主曲率的算法相似,本文以自由曲面上最大主曲率的求解算法进行说明,其算法流程如图3所示。
适应度函数:

|
(7) |
式中:k、
具体的遗传算法描述如下:
步骤1:设定初始种群数m、代表基因长度的二进制代码的位数n(以8位二进制为例进行说明)、交叉概率Pc、变异概率Pv,并随机产生二进制代码表示种群的个体,其中二进制代码位数不足的用0在前面补齐。
步骤2:将个体的二进制代码分解为关于参数u和v的单染色体,并计算u和v实际参数值,根据式(5)计算主曲率,以式(7)所得个体主曲率的适应度值作为评价指标,应用轮盘法淘汰不满足预设适应度值的个体。
步骤3:根据适应度函数,对适度应函数值较高的个体按轮盘法概率选择后进入下一代,其中,当代中的适应度函数值最大的个体及边界个体00000000、11111111直接进入下一代。
步骤4:根据所设定的交叉概率Pc、变异概率Pv对新一代种群进行交叉、变异操作。
步骤5:根据新一代种群重新计算主曲率。
步骤6:重复步骤2~5直至遗传算法结束,输出记录的最大主曲率值
 |
| 图2 接触轮磨削方式 Fig. 2 Grinding manners |
1.3 无干涉高效宽行加工的接触轮尺寸选取
通过上述算法求得自由曲面上的最大主曲率
| ${R_{\rm{m}}} = 1/{k_{\rm{m}}}$ | (8) |
接触轮宽度:
| $W \le 2\sqrt {2h \cdot {R_{\rm cmin }} - {h^2}} $ | (9) |
Rm应小于等于标准接触轮尺半径,W小于等于标准接触轮宽度,使用该接触轮对自由曲面进行磨削加工可满足无局部曲率干涉的自由曲面加工要求,有效避免因经验不足,选取接触轮尺寸不合适而造成的工件磨削损伤甚至报废;或因追求加工精度,选取接触轮尺寸过小而导致的自由曲面加工效率的低下。
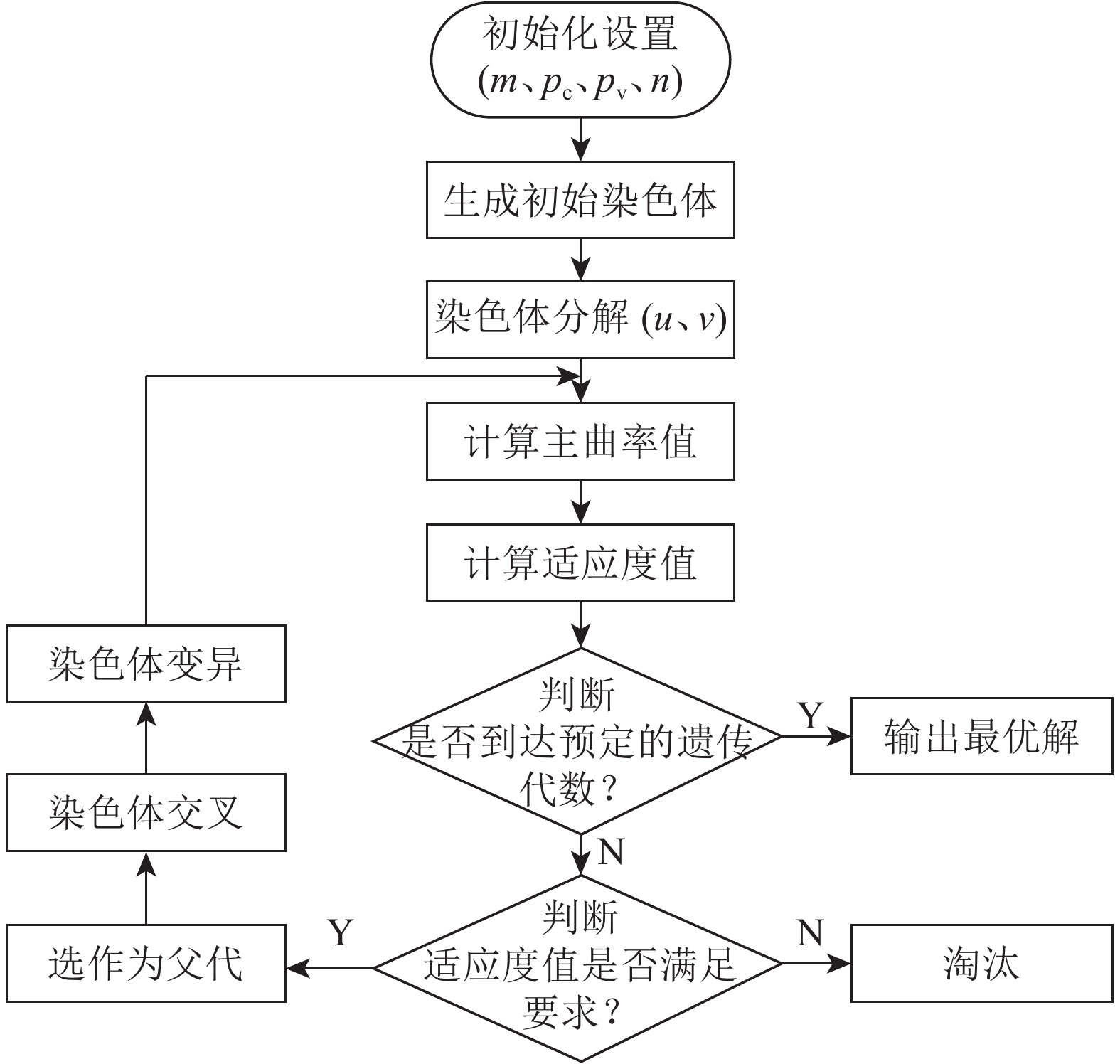 |
| 图3 遗传算法流程图 Fig. 3 Flow chart of genetic algorithm |
2 自适应宽行轨迹规划算法
普通的等参数线法轨迹规划方法由于其参数域内的直线转换到欧氏几何空间后变成曲线,且参数间隔固定的相邻两条等参数线刀轨在空间上不等距[10],因此在宽行加工中相邻轨迹间需有一定的搭接量。如何确定行距确保相邻两行刀轨的最小搭接量接近于零仍然是一个精密数控编程领域的技术难题。针对相邻刀轨间最小搭接量难题和横向宽行磨削加工的特性,通过有效计算各磨削点在第一主曲率方向上距离为加工行距的点,并将其作为相邻轨迹磨削点,即可实现各磨削点,在接触轮轴向的自适应,而且能巧妙避开宽行加工中求解最小搭接量的难题,保证了相邻刀轨之间行距的稳定性。
2.1 相邻磨削点的计算以接触轮宽度W作为磨削加工的行距,由前文可知,当前磨削点的相邻磨削点为其在第一主曲率方向上距离为W的点,已知曲面函数
第一、二主曲率方向矢量垂直:
| ${\mathit{\boldsymbol{P}}_1} \cdot {\mathit{\boldsymbol{P}}_2} = 0$ | (10) |
又已知当前磨削点与相邻磨削点构成的矢量沿第一主曲率方向且其距离为
| $\left\{ \begin{aligned}& \mathop {{C_{i,j}}{C_{i + 1,j}}} {\mathit{\boldsymbol{P}}_1} = W\\& \mathop {{C_{i,j}}{C_{i + 1,j}}} {\mathit{\boldsymbol{P}}_2} = 0\end{aligned} \right.$ | (11) |
应用Taylor公式将
| ${C_{{{i + }}1,{{j}}}} = {C_{i,j}} + {\mathit{\boldsymbol{S}}_u}' \cdot \Delta u + {\mathit{\boldsymbol{S}}_v}' \cdot \Delta v$ | (12) |
| $\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\text{令}\;\;T = - \frac{{{\mathit{\boldsymbol{S}}_v}' \cdot {\mathit{\boldsymbol{P}}_2}}}{{{\mathit{\boldsymbol{S}}_u}' \cdot {\mathit{\boldsymbol{P}}_2}}}$ | (13) |
代入式(12):
| $\Delta u = T \cdot \Delta v$ | (14) |
| $\Delta v = \frac{W}{{T \cdot {\mathit{\boldsymbol{S}}_u}' \cdot {\mathit{\boldsymbol{P}}_1} + {\mathit{\boldsymbol{S}}_v}' \cdot {\mathit{\boldsymbol{P}}_1}}}$ | (15) |
根据式(10)、(11)可求得相邻磨削点间关系为:
| $\left\{ \begin{aligned}& {u_{i + 1}} = {u_i} + \Delta u\text{,}\\& {v_{j + 1}} = {v_j} + \Delta v\end{aligned} \right.$ | (16) |
图4为本文所提出的轨迹规划示意图。由于某些叶片型面存在扭曲的特征,使得当前磨削点与后一磨削点在其第一主曲率方向上距离为行距的范围内相交,这种情况容易造成加工时磨头往复摆动产生加工震动而引起加工振纹缺陷,故本文提出一种将相邻磨削点参数信息进行交换以实现磨削点轨迹的柔顺自适应处理规划方法,效果如图5所示。其思路是通过遍历新磨削点,删除位于边界外的新轨迹磨削点,并插入新刀轨的边界点,遍历得到的新轨迹中的磨削点;并计算相邻磨削点之间是否满足步长精度要求,若不满足采用二分法插值,直至所有相邻磨削点满足步长要求后更新磨削点序列。
2.3 自适应磨削路径的生成步骤自由曲面自适应磨削路径规划的主要步骤如下:
1)先对复杂曲面模型进行特征识别并选择复杂曲面中较长的边界线作为刀具初始轨迹线,再按照最小步长以二分法对初始轨迹进行磨削点离散;
2)计算初始磨削点在第一主曲率方向上相距为行距的相邻磨削点;
3)对新得到的磨削点进行柔顺与插值处理;
4)重复步骤2)、3)直至磨削点覆盖整个曲面后,将磨削点轨迹转换为刀位点轨迹。
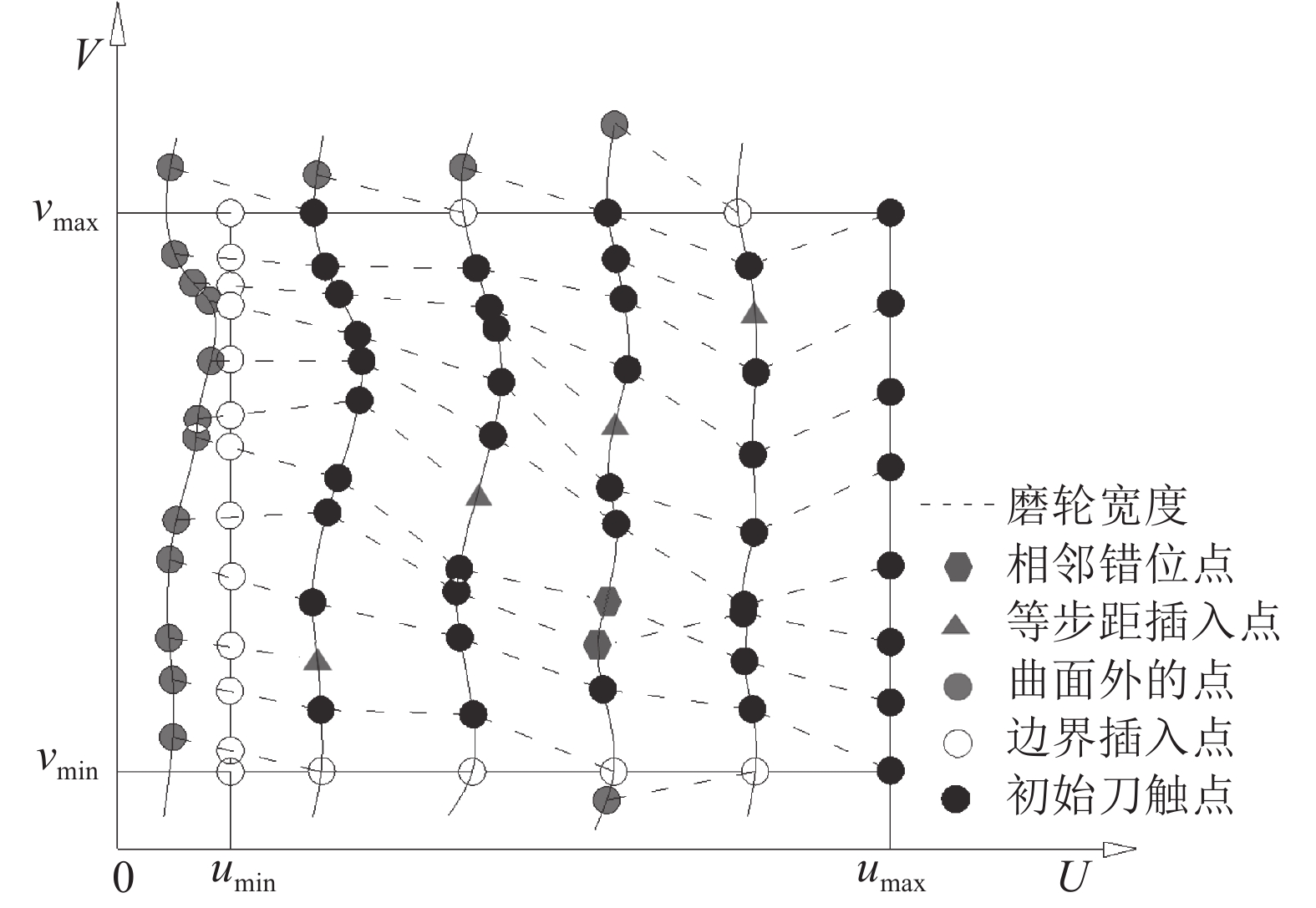 |
| 图4 自适应轨迹规划示意图 Fig. 4 Schematic diagram of adaptive trajectory planning |
 |
| 图5 柔顺自适应处理效果 Fig. 5 Flexible adaptive processing effect |
图6为对某航发叶片的单个曲面模型应用本文的轨迹规划方法与等参数轨迹规划方法(两种方法设置了相同加工行距与步距)的对比。
通过对比可以直观地发现,本文所提出的行距自适应轨迹规划的路径始终沿曲面上磨削加工点的主曲率方向变化,从而有效保证了加工时磨头与工件的最佳贴合,也很好地解决了等参数相邻轨迹在空间上不等距的问题。
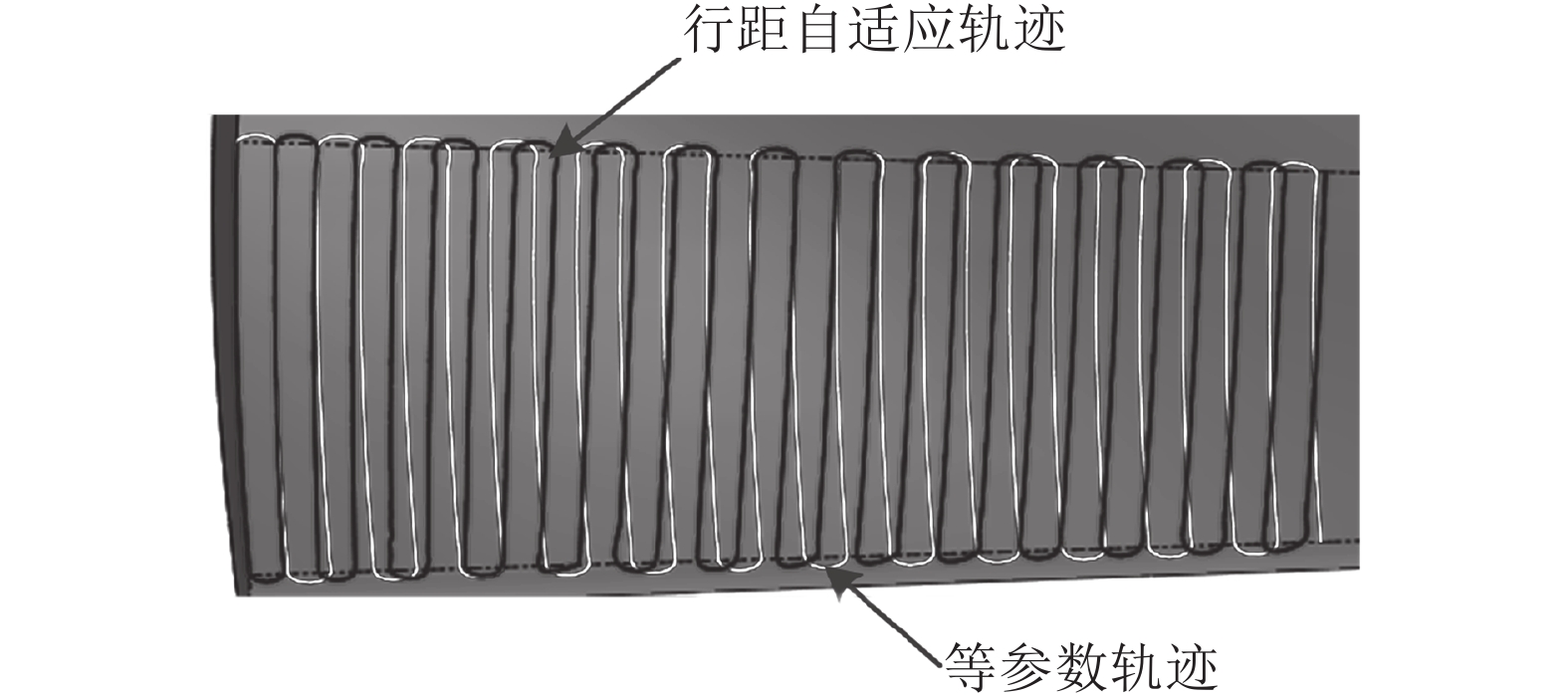 |
| 图6 轨迹规划应用图 Fig. 6 Application diagram of trajectory planning |
3 实验加工验证
应用本文所述的轨迹规划方法在某航空发动机企业的数控砂带磨床上对叶片、叶盆和叶背进行了加工实验验证。考虑到工程实际应用与加工效率及砂带本身的柔性接触等原因,对所用接触轮半径和宽度进行了适当放大,其磨削加工参数如表1所示。
| 表1 磨削加工参数 Tab. 1 Grinding parameters |
 |
 |
| 图7 磨削加工前后叶片全貌对比 Fig. 7 Comparison of blade profile before and after grinding |
 |
| 图8 磨削加工前后粗糙度轮廓图 Fig. 8 Roughness profile before and after grinding |
如图7所示,由磨削加工前后叶片全貌的对比可以发现,加工后叶片表面光整,无因曲率干涉等问题所引起的加工缺陷,加工质量较好。叶片加工前后分别应用Marsurf粗糙度轮廓仪对图8(a)中对应的测量位置进行检测,并对数据进行滤波处理后得到如图8(b)、(c)所示的粗糙度轮廓数据。
从图8中可以看出加工后表面粗糙度得到较大改善,其原因在于砂带磨粒通过在叶片工件表面金属层进行高速的滑擦、耕犁和挤压等复杂交互作用将工件表面的原有凸峰碾平,使其粗糙度轮廓变得更小、更均匀,从而有效降低了所加工表面的粗糙度,最终使得磨削加工后叶片型面的表面质量比加工前改善较大。
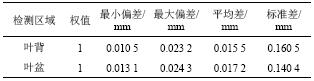
| 表2 截面加工前三坐标检测数据 Tab. 2 Test data of cross-section before grinding |
 |
| 表3 截面加工后三坐标检测数据 Tab. 3 Test data of cross-section after grinding |
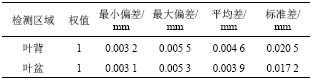 |
应用海克斯康global系列三坐标测量机对叶片加工前后进行误差检测。表2、3分别为叶片第5组截面加工前后的三坐标检测数据。
通过分析可知:叶背部分对应测点的最大误差由最初的0.023 2 mm降至0.005 5 mm,平均误差由0.015 5 mm降至0.004 6 mm;叶盆部分对应测点的最大误差则由最初的0.024 3 mm降至0.005 3 mm,平均误差由0.017 2 mm降至0.003 9 mm。根据上述对比可以发现,选用根据曲面自身特征优选的接触轮尺寸,可有效避免自由曲面加工中局部干涉与过切等问题;根据接触轮参数所确定的加工参数,使用提出的自适应轨迹规划方法进行加工可有效减少过切点数量,大大提高自由曲面的加工精度,有效保证航空发动机叶片型面精密加工技术要求。
4 结 论采用双倍体遗传算法对待加工曲面进行无曲率干涉磨轮尺寸优选,可有效避免磨削加工时的局部干涉,利用磨削加工时磨头与工件的最佳贴合机理进行基于磨削点行距的自适应轨迹规划,可在加工时通过对接触轮磨削姿势的控制,实现磨头与工件的最佳贴合,从而达到最佳的磨削效果。实验证明:基于误差精度控制方法确定加工参数并进行行距自适应轨迹规划,实现了曲面无残留、无过切的磨削加工,在充分保证加工精度的同时提高了加工效率,对其他自由曲面高效磨削加工应用具有一定的参考借鉴价值。
| [1] |
Wu Baohai, Luo Meng, Zhang Ying. Advances in tool path planning techniques for 5-axis machining of sculpture surfaces[J]. Journal of Mechanical Engineering, 2008, 44(10): 9-18. [吴宝海, 罗明, 张莹. 自由曲面五轴加工刀具轨迹规划技术的研究进展[J]. 机械工程学报, 2008, 44(10): 9-18. DOI:10.3321/j.issn:0577-6686.2008.10.002] |
| [2] |
Ng T J,Lin W J,Chen X Q,et al.Intelligent system for turbine blade overhaul using robust profile re-construction algorithm[C]//Proceedings of the 8th International Conference on Control,Automation,Robotics and Vision,2004.New York:IEEE,2004:178–183.
|
| [3] |
黄云,黄智.现代砂带磨削技术及工程应用[M].重庆:重庆大学出版社,2009:30–35.
|
| [4] |
Xu Jinting, Liu Weijun, Qiu Xiaojie. Isoparametric and spiral tool-path for free-form surfaces machining[J]. Journal of Mechanical Engineering, 2010, 46(3): 148-151. [徐金亭, 刘伟军, 邱晓杰. 自由曲面加工中的等参数螺旋轨迹生成方法[J]. 机械工程学报, 2010, 46(3): 148-151.] |
| [5] |
Chen Zhitong, Le Yi, Xu Rufeng. Point error control line processing algorithm[J]. Journal of Mechanical Engineering, 2011, 47(1): 117-123. [陈志同, 乐毅, 徐汝锋. 中点误差控制宽行加工算法[J]. 机械工程学报, 2011, 47(1): 117-123.] |
| [6] |
He Ying, Chen Zhitong, Wu Xianzhen. ISO-parametric tool path overlapping method for sculptured surfaces in wide strip machining[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(4): 1142-1148. [贺英, 陈志同, 吴献珍. 复杂曲面宽行加工等参数线刀轨精确搭接方法[J]. 航空学报, 2014, 35(4): 1142-1148.] |
| [7] |
Yang Jianhua, Zhang Dinghua, Zhang Juan. An approach to strip-maximization machining based on tolerance co-ntraints for sculptured surfaces[J]. Journal of Mechanical Engineering, 2013, 49(3): 130-136. [杨建华, 张定华, 张娟. 基于公差约束的复杂曲面宽行加工方法[J]. 机械工程学报, 2013, 49(3): 130-136.] |
| [8] |
Li H,Zhang Y.Automatic tool-path generation in 5-axisfinish cut with multiple cutters[C]//Proceedings of the 2009 IEEE International Conference on Virtual Environments,Human-Computer Interfaces and Measurement Systems.Washington:IEEE,2009:210–213.
|
| [9] |
Chiou C,Lee Y. A machining potential field approach to tool path generation for multi-axis sculptured surface machining[J].Computer Aided Design,2002.34(5):357–371.
|
| [10] |
Lasemi A, Xue D, Gu P. Recent development in CNC machining of freeform surfaces:A state-of-the-art review[J]. Computer Aided Design, 2010, 42(7): 641-654. DOI:10.1016/j.cad.2010.04.002 |
 2017, Vol. 49
2017, Vol. 49

