与传统机械密封相比,干气密封具有很高的技术含量和优势,具有磨损小、泄漏小、寿命长、能耗低、操作简单且可靠性高等诸多优点[1],被广泛应用,研究者众多。Renat等[2]研究了干气密封操作的动态过程,分析了在轴向转子振动条件下密封的开启力。Ibrahim等[3]等用数值模拟方法分别研究了等深螺旋槽和不等深锥度螺旋槽干气密封在不同膜厚下的密封性能变化,结果表明沿径向和周向分布的锥度螺旋槽端面开启力和泄漏率会同时降低。Fairuz等[4]利用CFD对CO2真实气体在超临界和远离临界状态下的密封性能进行了研究,发现不同操作条件下密封介质密度的变化高达39.5%,其压力分布和泄漏率有一些改变。Su等[5]对可压缩层流工况,采用热固流耦合的多物理模型研究了梯形对称双向干气密封的热-流体动力特性,并对比分析了端面流场的压力、温度和速度的局部变化。许静[6]对高压工况下干气密封的气膜特性、端面变形机理和变化规律开展了理论与实验研究。但上述的研究分析往往是在假设平行间隙的前提下进行的,实际上在力边界和热边界条件下,运行中的密封环会发生变形[7]。苏虹等[8]考虑力变形,获得相应的气膜厚度近似表达式,并分析了力变形下泄漏量的变化情况,发现考虑力变形得到的泄漏量更接近试验值。宋鹏云等[9]研究变形后螺旋槽干气密封的气膜压力分布情况,并与平行间隙情况进行了对比,发现密封端面间形成非平行间隙时,其气膜压力分布会发生改变,但在密封面的区域内存在某一半径
目前,对于端面变形后的气膜流场的分析不多,对于变形后干气密封的密封机理的研究还不够深入。由于端面间隙流场是极小尺度,目前的测量手段很难对微米级气膜的压力、变形等做出精确测量,并且任何接触式的测量方法都会对对该流场造成一定的破坏,不能获得准确的流场。陈志等[11]采用自定义函数找到了端面密度变化规律,发现压力较高的工况密度的变化明显影响密封性能。Meng等[12]研究了流体黏度在激光端面微结构平行表面中对压力分布和承载力方面的作用,结果表明黏度对楔形效应起着重要作用。
作者采用CFD,考虑了介质密度和黏度的变化的影响,对收敛型端面气膜间隙进行流场数值模拟。重点分析锥形间隙下,端面开启力产生的原理,并讨论了端面间隙收敛锥角大小对干气密封性能的影响。
1 干气密封端面模型结构及参数图1为干气密封的典型结构图。该密封结构由动环、静环、弹簧、静环座、O型圈、轴和轴套组成。固定在轴套上随转轴一起转动的动环和以弹性元件和密封圈为支撑的静环(补偿环)共同构成了端面密封副。动环表面开有流体动压槽的密封端面,槽深一般为几个微米至十几微米。
 |
| 图1 典型干气密封结构图 Fig. 1 Schematic drawing of dry gas seal |
图2为典型螺旋槽干气密封动环端面结构图。主要包括流体动压槽、密封堰、密封坝3部分,三者共同作用产生气膜的静、动压承载能力;其中,流体动压槽起着泵送气体形成气膜的作用,密封堰阻止流体沿圆周向泄漏,密封坝阻止了流体沿半径方向的泄漏。
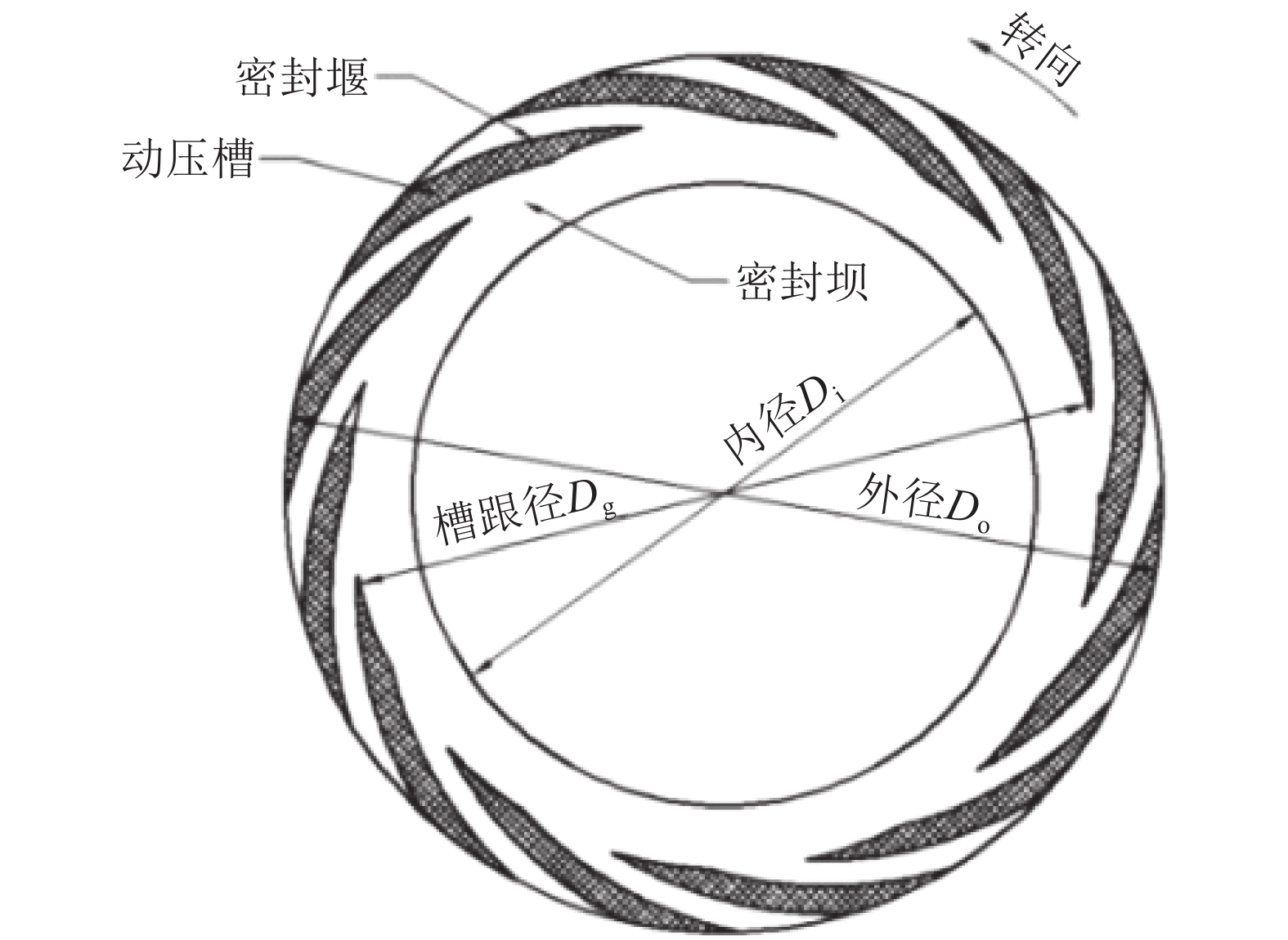 |
| 图2 干气密封动环端面结构图 Fig. 2 Rotational ring end face schematic drawing of a dry gas seal |
干气密封的参数主要包括端面结构参数、操作参数和性能参数。结构参数主要用于描述干气密封的槽型结构,有螺旋角、槽数、槽深、槽台宽比、槽长坝长比;操作参数是指干气密封的运行工况,有转速、压差、介质温度、介质黏度、介质密度等;评价干气密封性能的好坏通常用性能参数,常用的有开启力、泄漏率、气膜刚度和刚漏比。
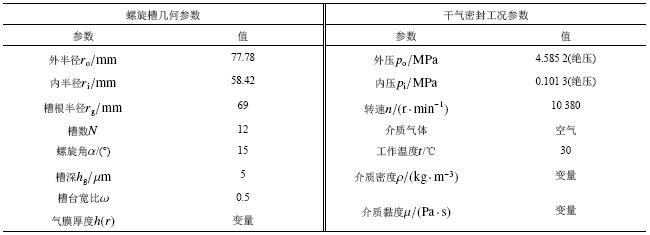
本文按照文献[7]给出的螺旋槽干气密封端面结构尺寸进行分析,并与该文献中的实验值进行对比,其密封的几何参数和实验工况参数如表1所示。
| 表1 螺旋槽干气密封几何参数和工况参数 Tab. 1 Geometric parameters and operating parameters of spiral groove dry gas seal |
 |
2 计算模型及网格划分 2.1 理论模型假设
干气密封理想的工作状态是动、静环保持平行,形成稳定的平行气膜间隙。但是由于密封环受到压力、端面温差等的作用,很难形成真正的平行间隙。实际工作状态下,密封环的变形,主要是径向的偏转,端面沿径向方向的变形近似呈线性变化,两端面将形成一个锥角,气膜流场呈收敛型楔形状。文献[13]研究表明,密封端面的变形非常接近线性,只有靠近内径处的静环端面会出现一定的波动,不过端面波动变形尺度较小,对整个气膜流场的影响不大[4,7],如图3所示,为便于分析计算,假设密封端面变形为线性,并定义收敛型间隙气膜锥角为
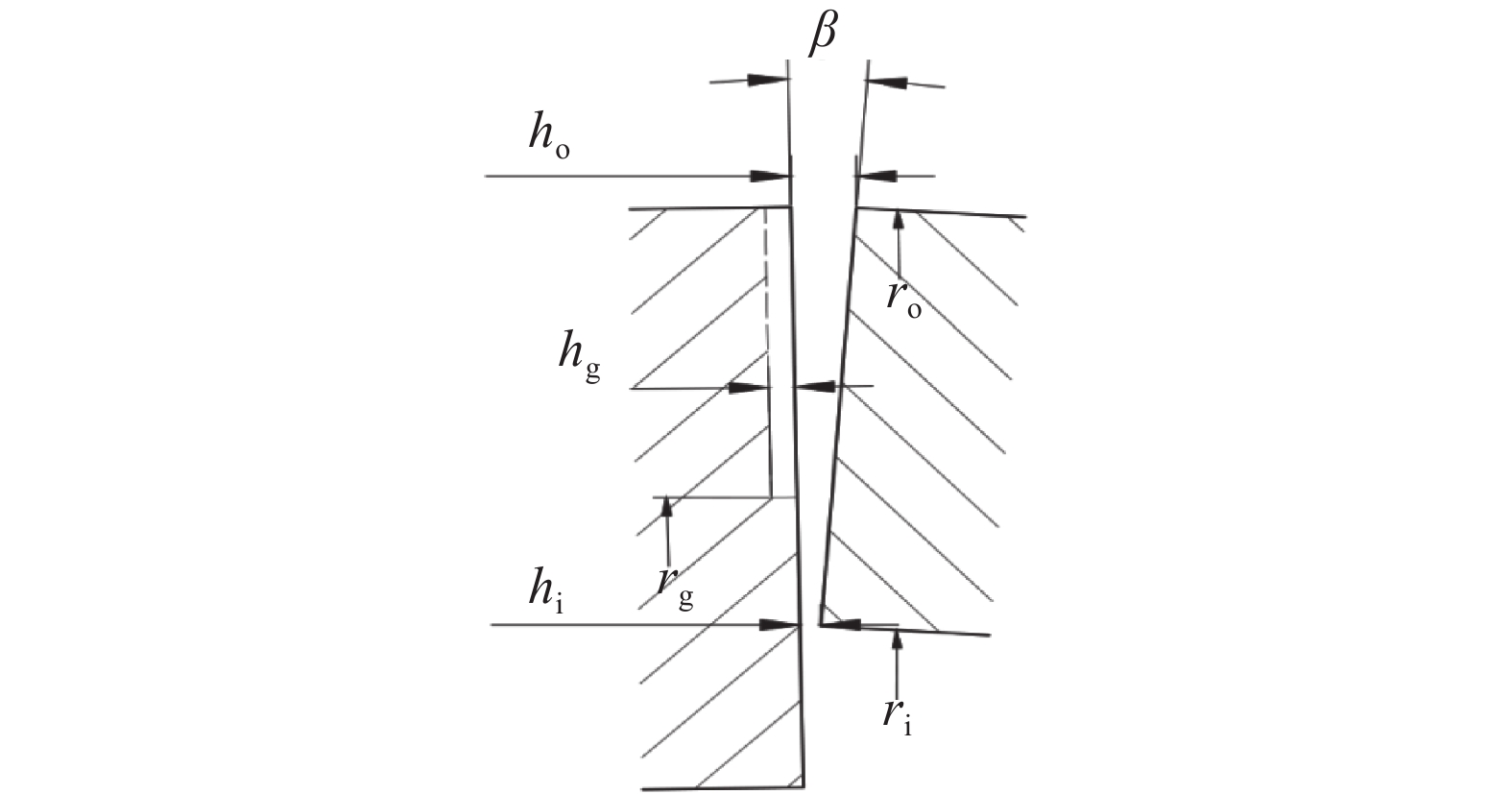 |
| 图3 密封环及楔形间隙示意图 Fig. 3 Seal ring and wedge gap diagram |
当密封环发生变形后,气膜厚度随着端面半径和气膜锥角而变化,而且气膜锥角
| $h(r) = {h_{\rm i}} + \tan\; \beta (r - {r_{\rm i}})$ | (1) |
槽区的气膜厚度为:
| $h(r) = {h_{\rm i}} + \tan \,\, \beta (r - {r_{\rm i}}){\rm{ + }}{h_{\rm g}}$ | (2) |
螺旋槽干气密封端面气膜压力分布如下。
在槽区
| $\frac{{{\rm d}p}}{{{\rm d}r}} = \frac{{ - 6{g_1}\mu \omega }}{{{h^2}}}r + \frac{{6\mu Q{g_7}RT}}{{\text{π} {h^2}{g_5}}} \times \frac{1}{{pr}}$ | (3) |
在密封坝区
| $\frac{{{\rm d}p}}{{{\rm d}r}} = \frac{{6\mu QRT}}{{\text{π} {h^{\rm{3}}}}} \times \frac{1}{{pr}}$ | (4) |
式中:
分析该密封端面间隙流场首先要确定其理论模型,对端面流场做稳态分析,根据流体力学基本理论和计算需要,对计算模型做如下设定:
1)端面介质连续且等温;
2)壁面为无滑移边界条件,即与端面接触处的介质相对速度为0;
3)由于介质为气体,因此忽略介质的体积力;
4)忽略密封运行过程中的扰动对气膜流场流动的影响;
5)假设该密封内端面流场流体是层流流动[15]。
根据上述假设可以将端面间隙气膜流场的运动方程(即Navier–Stokes方程)简化为下面的形式:
| $\left( { {v} \cdot \nabla } \right){v} = - \frac{1}{\rho }\nabla p + v{\nabla ^2}{v}$ | (5) |
式中:
螺旋槽干气密封端面流场为循环对称结构,周向均匀分布为N个槽。本文建立的流场3维几何模型采用了循环对称结构,选取槽数十二分之一的部分即一个槽区及与之相连的坝区作为研究对象,平行间隙气膜几何模型如图4所示。对于楔形气膜模型,在动环端面侧,由于螺旋槽的存在,如果考虑动环的变形,在建模及网格划分时就比较困难。因为干气密封动环一般为硬质材料,相比静环的碳石墨而言其弹性模量E大很多,故变形要小很多。所以在几何模型建立时可忽略动环的变形,图5为收敛型间隙气膜计算几何模型。
 |
| 图4 平行间隙气膜几何模型(轴向放大1 000倍) Fig. 4 Parallel gap model(axial magnification 1 000 times) |
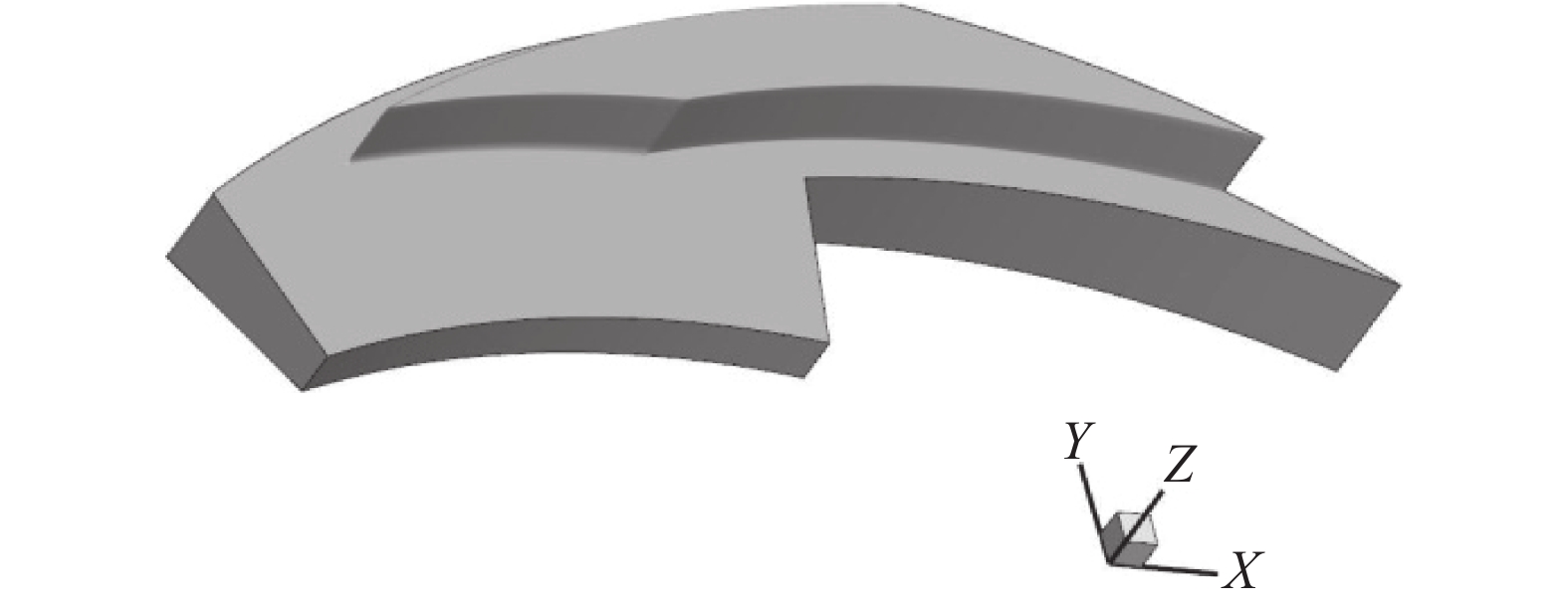 |
| 图5 收敛型间隙气膜几何模型(轴向放大1 000倍) Fig. 5 Wedge gap model(axial magnification 1 000 times) |
2.2 网格划分
将计算几何模型进行网格划分,但是模型的轴向厚度只有几微米,与径向尺寸相差巨大,传统的直接在模型上的网格划分显然不可取,本文模型利用ANSYS软件由四边形面网格拉伸而得六面体网格,平行及楔形计算区域网格如图6所示。本文计算过程需要多次计算模型的建立,所以几何模型和网格划分均由APDL(ANSYS parameter design language)即ANSYS参数化设计语言完成。
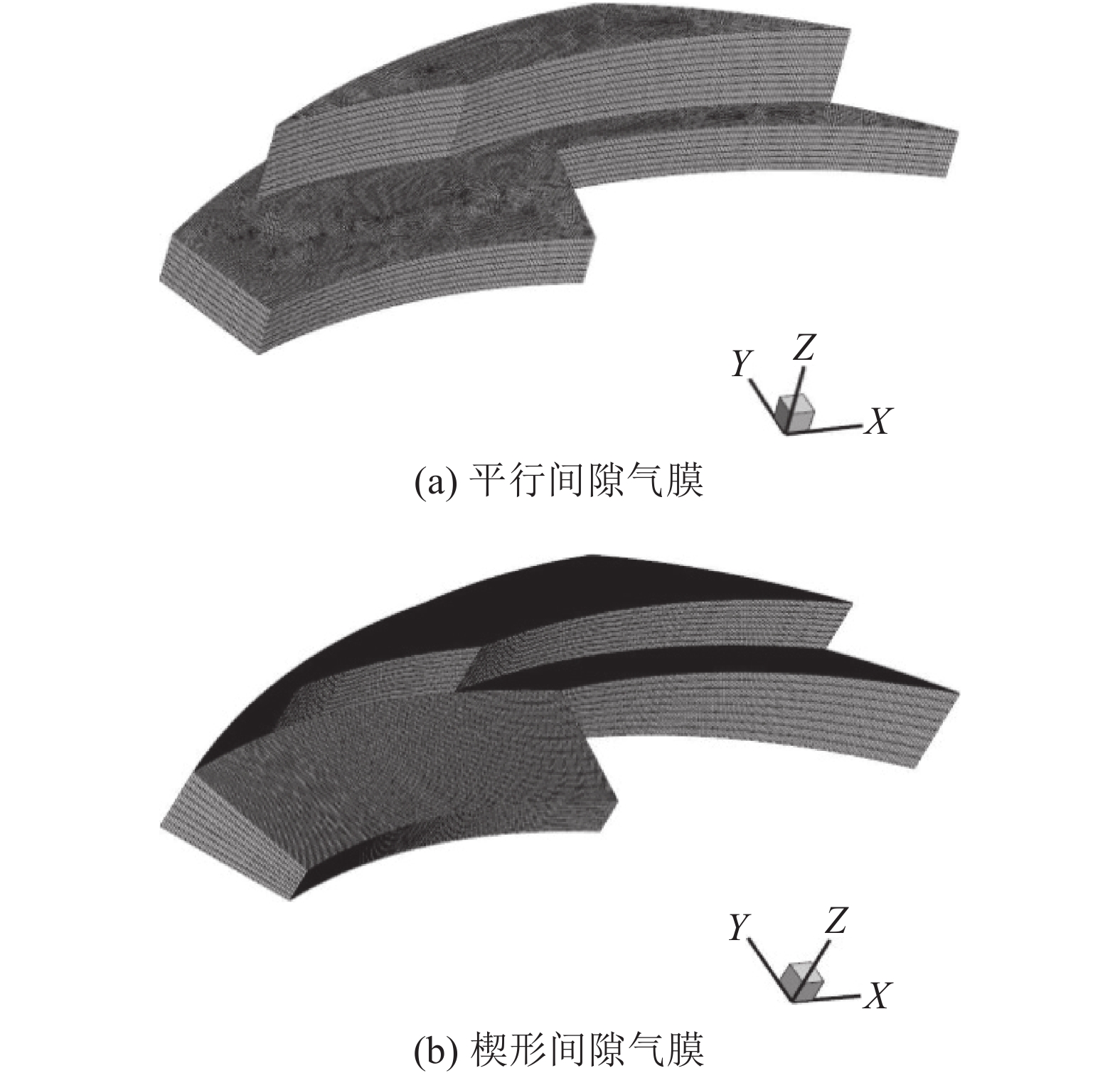 |
| 图6 计算区域网格(轴向放大1 000倍) Fig. 6 Mesh of computational domain(axial magnification 1 000 times) |
3 数值计算 3.1 边界条件
由于采用了周期对称结构,因此除了压力入口,压力出口以及动环端面和静环端面以外,还有两个循环周期边界。满足条件:
| $\begin{array}{l}P(r = {r_{\rm o}},\theta ,{\textit{z}}) = 4.585\;2\;{\rm MPa},\\P(r = {r_{\rm i}},\theta ,{\textit{z}}) = 0.101\;3\;{\rm MPa},\\\psi ({r_1},{\theta _1},{{\textit{z}}_1}) = \psi ({r_2},{\theta _2},{{\textit{z}}_2}),\\{\theta _1} = {\theta _2} + 2\text{π} /N\end{array}$ | (6) |
式中:
采用无滑移边界条件,动环面为旋转壁面,静环面为静止面,外径处为压力入口,内径处为压力出口及周期边界,如图7所示。
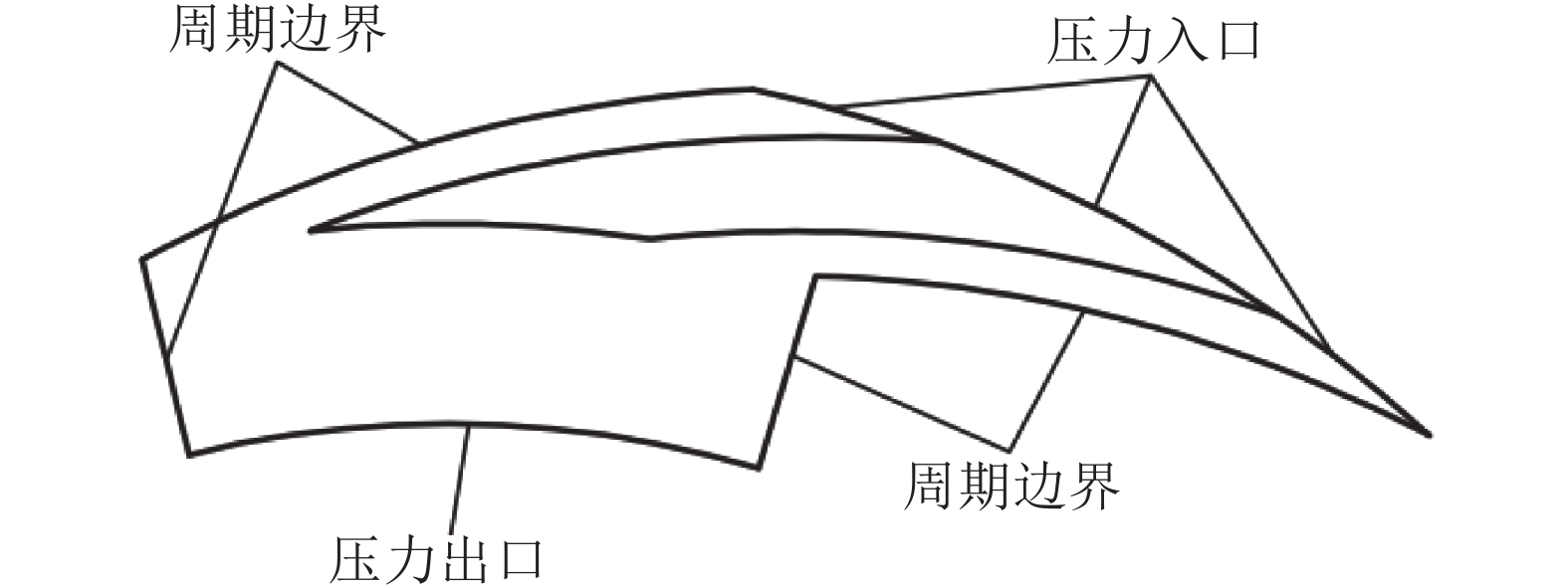 |
| 图7 边界条件 Fig. 7 Boundary conditions |
3.2 局部密度及黏度的确定
传统的干气密封端面流场的数值模拟方法多将端面间介质参数设为恒定密度和黏度,而实际上介质的密度和黏度是随着介质压力和温度的变化而变化的。由于干气密封稳定运转后端面流场的温度变化不大,因而介质密度及黏度受温度变化的影响很小[16]。但端面间的介质压力的变化是十分明显的,以文献[7]中密封端面气膜厚度为3.05 μm时流场压力分布为例,端面外径进口处压力约为4.6 MPa(绝压),端面内径出口处压力约为0.1 MPa(绝压),密封介质为空气,假设端面等温都为45 ℃。查得端面进口和出口处压力下空气的密度分别为50.37和1.13 kg/m3,前者是后者的近45倍,可见端面流场介质密度变化之大。在高压及超高压工况下密度的变化在进出口边界将更为明显,所以,将介质密度和黏度设定为压力的函数是必要的,数值模拟可以得到更真实的结果。
将介质的密度和黏度设定为压力的函数,利用用户自定义函数UDF加载到FLUENT中进行计算。首先,通过ASPEN软件查得介质在某恒定温度、不同压力下对应的密度和黏度,压力选取范围为0.1~12 MPa,每隔0.1 MPa获取其相应压力下的密度和黏度,然后,将得到的120组数据导入EXCEL中拟合出密度和黏度随压力变化的公式。为保证拟合公式的精确性,结合数据特点,密度采用二次多项式拟合,黏度采用三次多项式拟合。其中,编写得到的空气在30℃下密度和黏度随压力变化的函数分别见式(7)、(8),将压力值带入密度和黏度随压力变化的公式就能得到该压力下介质的密度和黏度。
| $\rho {\rm{ = - 2}}{\rm{.13}} \times {\rm{1}}{{\rm{0}}^{ - 2}}{p^2} + 11.71p - 2.29 \times {10^{ - 1}}$ | (7) |
| $\begin{aligned}[b]\mu = & - 3{\rm{.880\;8}} \times {\rm{1}}{{\rm{0}}^{ - {\rm{10}}}}{p^{\rm{3}}} + {\rm{1}}{\rm{.573\;7}} \times {\rm{1}}{{\rm{0}}^{{\rm{ - 8}}}}{p^{\rm{2}}}{\rm{ + }}\\[8pt]& 1{\rm{.058\;5}} \times {10^{ - {\rm{7}}}}p + 1.881\;6 \times {10^{ - 5}}\end{aligned}$ | (8) |
式中:
另外,在Fluent计算中,为使压力结果稳定,所以必须在压力方程中添加声速公式,声速即等熵变化时,压力对密度的导数。根据空气动力学[17],一般情况下的声速a可以定义为:
| $a = \sqrt {\gamma \frac{p}{\rho }} $ | (9) |
式中:
干气密封在实际工作状态下,气膜锥角和厚度会随着工作参数的变化而发生改变。为研究气膜锥角的大小对干气密封的影响,在相同闭合力条件下,寻找不同锥角所对应的气膜厚度,需要根据条件进行迭代计算,图8为计算流程图。
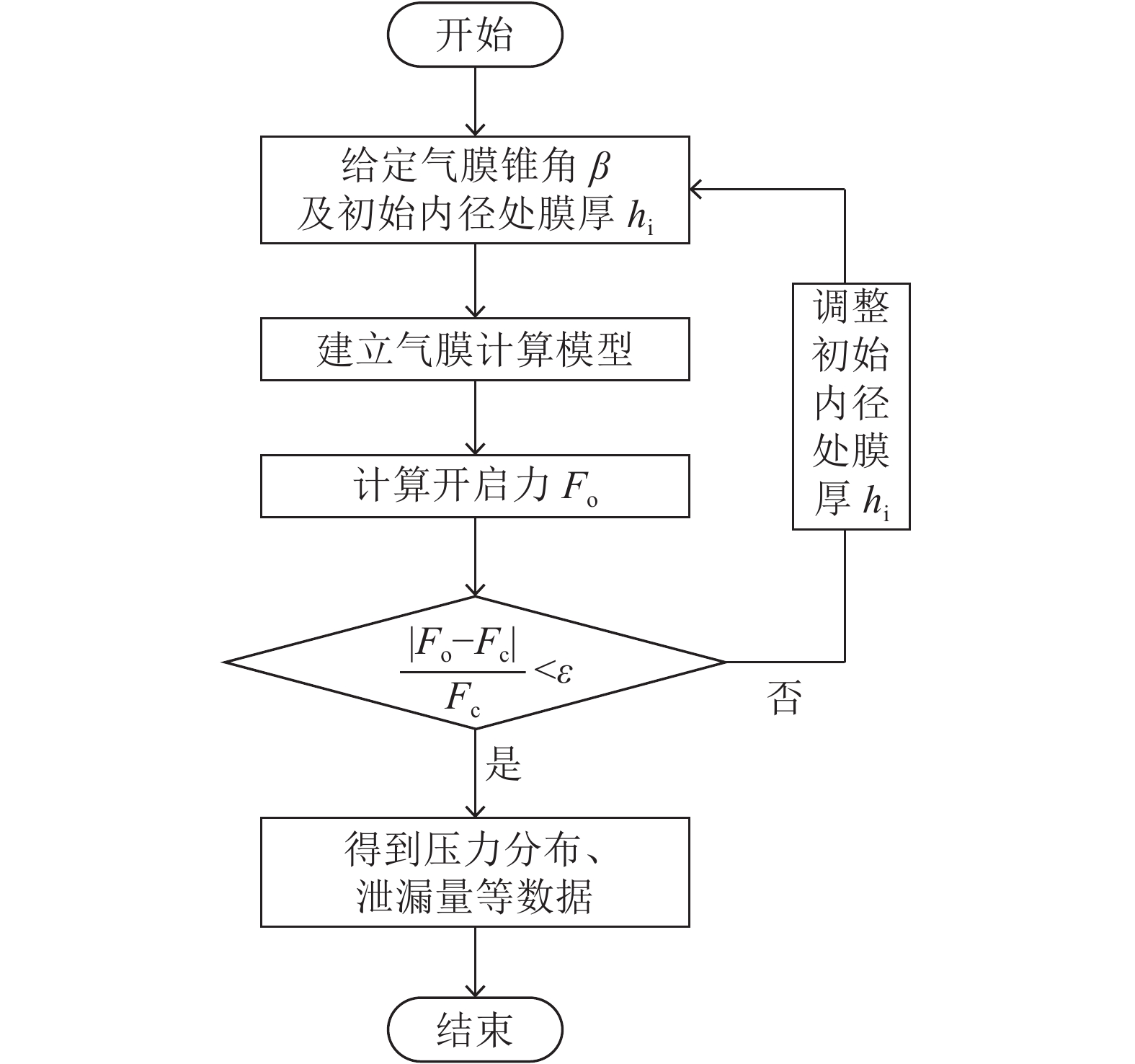 |
| 图8 计算流程图 Fig. 8 Calculation flow chart |
干气密封稳定运转时,密封浮动环轴向受力平衡,密封端面开启力
| $error = \frac{{\left| {{F_{\rm o}} - {F_{\rm c}}} \right|}}{{{F_{\rm c}}}} < \varepsilon $ | (10) |
采用文献[7]中的参数,利用本文上述方法,对文献中的平行间隙和气膜锥角为0.000 25 rad下的收敛型间隙气膜进行模拟计算并与文献中实验值验证。为验证网格大小对模拟结果的影响,用不同网格尺寸模拟平行间隙得出的开启力及计算时间如图9所示。发现随着网格尺寸的减小,开启力变化很小,模拟时间在网格尺寸为0.2 mm后急剧增加,综合考虑计算时间和精度,本文网格尺寸采用0.2 mm,此时平行间隙模型网格数为440 363,节点数为487 048;0.000 25 rad下的收敛型间隙模型网格数为644 408,节点数为693 128。
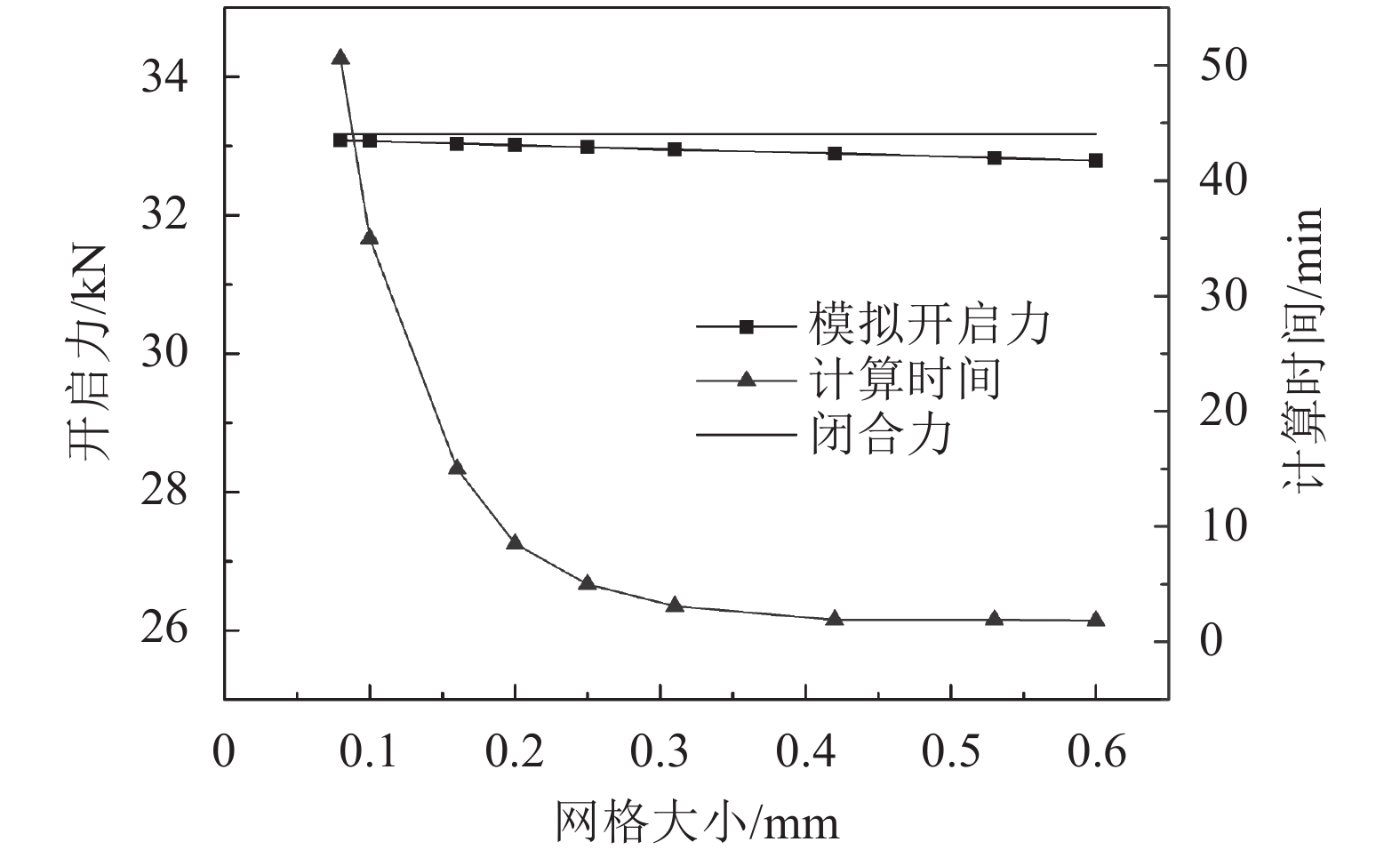 |
| 图9 平行间隙网格尺寸的独立性验证 Fig. 9 Independence verification of parallel gap grid size |
4.2 锥角对气膜压力分布、膜厚和泄漏率的影响
计算得到
从图10~11中可以看出,平行间隙时气膜产生了明显的动压效应,随着半径的增大,压力先增大后减小,在槽根处最大压力值为5.48 MPa,高于介质压力4.58 MPa;锥角较小时即小于0.000 15 rad时,最大压力在槽根部;而气膜锥角
 |
| 图10 不同间隙下气膜压力分布云图 Fig. 10 Pressure distribution of gas film under different gaps |
 |
| 图11 不同锥角时的气膜压力分布 Fig. 11 Pressure distribution at different film angles |
相同开启力条件下,不同气膜锥角下的内径处膜厚(
可以看到端面内径处膜厚随着锥角的变大有个先减小后增大的过程,说明不是任何角度的楔形气膜都如文献[7]中那样,内径处膜厚都比平行间隙时大;最小泄漏率出现在0.000 02 rad左右,平行间隙时的泄漏率与0.000 05 rad时相等,与文献[7]中平行间隙的泄漏率
| $\begin{aligned}[b]h(r) = & - 3.373 \times {10^9}{\beta ^3} +2.299 \times {10^7}{\beta ^2} - \\ &3.659 \times {10^3}\beta +2.586 + \tan \,\, \beta (r - {r_i})\end{aligned}$ | (11) |
| $\begin{aligned}[b]Q = & 7.042 \times {10^7}{\beta ^3} - 1.520 \times {10^4}{\beta ^2}+\\ & 2.121\beta {\rm{ }} + {\rm{ }}2.878 \times {10^{ - 4}}\end{aligned}$ | (12) |
式中:
可见气膜锥角较大时,泄漏量会很大,因此干气密封的设计要尽可能减小密封端面的变形,让端面气膜锥角保持在较小范围内,否则,密封会因为泄漏量过大而失效。根据泄漏率的变化规律,端面锥角在0.000 30 rad后泄漏率急剧增加,建议气膜锥角保持在0.000 30 rad以内。
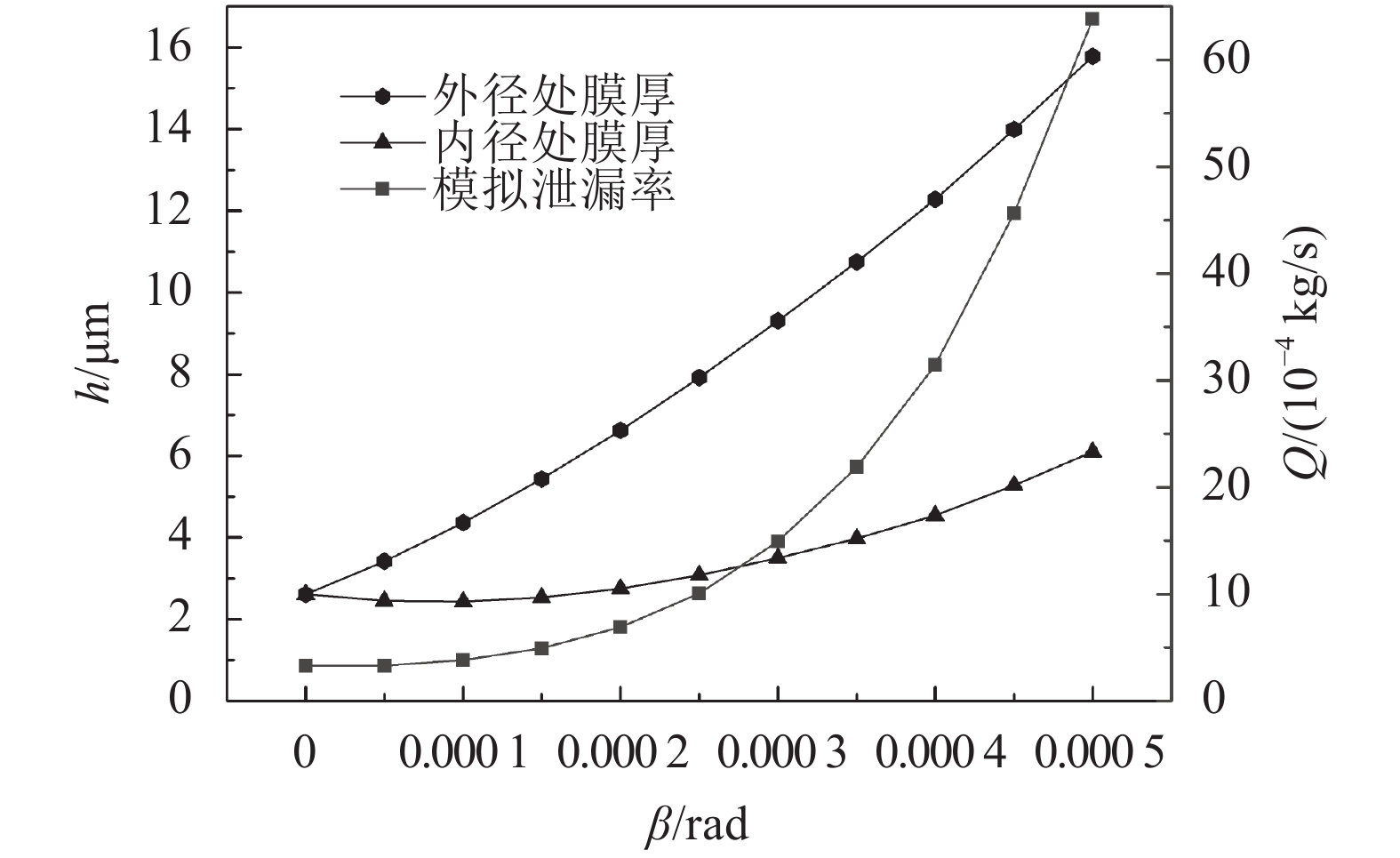 |
| 图12 气膜锥角对密封性能的影响 Fig. 12 Effect of film angles on sealing performance |
4.3 螺旋槽动压效应与楔形效应
分析图12中出现气膜厚度增加、泄漏量增大的现象,是收敛型楔形间隙产生了楔形效应[18]。首先讨论两个无槽的端面,平行间隙时两平行表面间的任意流通截面处的流量均相等,介质的流动只是由于压差所造成的,称为压差流,对外载荷只承受压差流作用;而当相互倾斜的两表面形成楔形收敛间隙时,若各气膜流层的速度分布规律仍相同,由于进出口膜厚的差异,就会导致介质流入大于流出,产生过剩流量,对于接近不可压缩的流体介质,过剩流体必将由进出口两端截面处被挤出,这种因压力导致的流动称之为压力流。收敛间隙中流体介质所产生的动压力是可以稳定存在的,这种由于黏性的流体介质流入楔形收敛间隙而造成的动压力效应就叫流体动力润滑的楔形效应[12,19]。因此,端面开槽的干气密封楔形间隙对外载荷承受压差流和压力流的共同作用,所以在相同的闭合力条件下,气膜总体厚度增加、泄漏量增大。
而且随着气膜锥角的增大,周向旋转在端面产生的动压效应减弱,径向楔形效应增强。为了更清晰地分析沟槽动压效应及楔形效应的作用,将计算模型的动环旋转速度假设为0 r/min,其他边界条件不变,则此状态下周向旋转引起的动压效应消失,在压力边界条件下流体流动所形成的气膜压力由楔形效应产生,也就是楔形效应的作用。动环旋转时的压力减去动环静止条件下的压力,这个差值就是沟槽周向动压效应的作用。图13为气膜锥角分别在0、0.000 05、0.000 15、0.000 35 rad时动环两种条件下的压力分布,明显可以发现随着气膜锥角的增加,动环旋转比动环静止条件下的压力增量减小,动环静止时的气膜压力分布增加,即周向旋转动压效应减弱,径向楔形效应增强;当气膜锥角较大时,两种条件下的压力分布已经非常接近,说明沟槽旋转产生的周向动压效应的作用已经很小,端面的打开主要是径向楔形效应的作用。因此,由于气膜锥角的增大,气膜绝对厚度增加较大,动环螺旋槽旋转所引起的动压效应明显下降,径向楔形效应的作用明显增强,并逐渐起主要开启作用。
 |
| 图13 不同气膜锥角下两种条件的气膜压力分布对比 Fig. 13 Contrast of pressure distribution under two conditions of different film angles |
5 结 论
1)用本文方法建立干气密封收敛型气膜流场模型,并把介质密度和黏度设定为压力的函数进行模拟计算是可行的,可以得到与实际工况更为接近气膜流场。
2)干气密封在气膜平行时沟槽的动压效应最好;而真实端面间隙为收敛型楔形气膜,气膜锥角的变化会引起端面压力分布发生改变,表现为连续光滑的上凸曲线形态,锥角较小时最大压力在槽根部。与平行间隙相比,收敛型气膜某一半径处压力保持不变,在小于此半径的区域,气膜压力随着气膜锥角的增大而增大,在大于此半径的区域,气膜压力随着气膜锥角的增大而减小;螺旋槽槽根处的压力变化最大,并且随着气膜锥角的增大,压力明显下降,但下降速度越来越慢。
3)在相同的闭合力条件下,随着气膜锥角的增大,总体气膜厚度增加,而端面内径处膜厚先减小后增加,外径处膜厚和泄漏量随着锥角的增大一直增加,并且在某一锥角后泄漏量增加明显,所以密封的设计要尽可能控制密封端面的变形,让端面气膜锥角保持在较小范围内,这样密封端面在打开的同时保持着较小的泄漏量,当
4)随着气膜锥角
| [1] |
Wasser J R. Dry seal technology for rotating equipment[J]. Lubrication Engineering, 1994, 50(3): 247-252. |
| [2] |
Renat R B, Sergey V F. Advanced dynamic model development of dry gas seal[J]. Procedia Engineering, 2017, 176: 344-354. DOI:10.1016/j.proeng.2017.02.331 |
| [3] |
Ibrahim S, Mohamed G, Mohamed A. Three dimensional computational study for spiral dry gas seal with constant groove depth and different tapered grooves[J]. Procedia Engineering, 2013, 68: 205-212. DOI:10.1016/j.proeng.2013.12.169 |
| [4] |
Fairuz M, Z J. The influence of real gas effects on the performance of supercritical CO2 dry gas seals
[J]. Tribology International, 2016, 102: 333-347. DOI:10.1016/j.triboint.2016.05.038 |
| [5] |
Su H, Rahmani R, Rahnejat H. Thermohydrodynamics of bidirectional groove dry gas seals with slip flow[J]. International Journal of Thermal Sciences, 2016, 110: 270-284. DOI:10.1016/j.ijthermalsci.2016.07.011 |
| [6] |
Xu Jing.Analytical and experimental investigations on the end face deformation mechanisms for high pressure sprial grooved dry gas seals[D].Hangzhou:Zhejiang University of Technology,2014. [许静.螺旋槽干气密封高压端面变形机理的理论与实验研究[D].杭州:浙江工业大学,2014.] http://cdmd.cnki.com.cn/article/cdmd-10337-1015502449.htm
|
| [7] |
Gabriel R P. Fundamentals of spiral groove non-contacting face seals[J]. Recation Engineering, 1994, 50(3): 215-224. |
| [8] |
Su Hong,Ding Xuexing,Zhang Haizhou,et al.Gas membrane flow field approximate calculation and analysis of spiral groove dry gas seal on the force distortion[J].Journal of Engineering Mechanics,2013,30(S1):279–283. [苏虹,丁雪兴,张海舟,等.力变形下螺旋槽干气密封气膜流场近似计算及分析[J].工程力学,2013,30(增刊1):279–283.] http://kns.cnki.net/KCMS/detail/detail.aspx?filename=gclx2013s1057&dbname=CJFD&dbcode=CJFQ
|
| [9] |
Song Pengyun, Li Ying, Ma Ailin. An approximate analytical method of gas film pressure in non-parallel gap of spiral groove dry gas seal[J]. Journal of Drainage and Irrigation Machinery Engineering, 2015, 33(12): 1049-1055. [宋鹏云, 李英, 马爱琳. 螺旋槽干气密封端面非平行间隙压力分布的近似解析计算[J]. 排灌机械工程学报, 2015, 33(12): 1049-1055. DOI:10.3969/j.issn.1674-8530.15.0081] |
| [10] |
Blasiak S, Zahorulko A V. Aparametric and dynamic analysis of non-contacting gas face seals with modified surfaces[J]. Tribology International, 2016, 94: 126-137. DOI:10.1016/j.triboint.2015.08.014 |
| [11] |
Chen Zhi, Gao Yunhao, Zhao Peng. Numerical simulation of flow field for high pressure dry gas seals[J]. Advanced Engineering Sciences, 2017, 49(2): 254-261. [陈志, 高昀皞, 赵鹏. 高压干气密封流场数值模拟[J]. 工程科学与技术, 2017, 49(2): 254-261.] |
| [12] |
Meng Xiangkai. On the effect of viscosity wedge in micro-textured parallel surfaces[J]. Tribology International, 2017, 107: 116-124. DOI:10.1016/j.triboint.2016.11.007 |
| [13] |
Xu Jin, Peng Xudong, Bai Shaoxian. Analysis of structural factor effecton torsion deformation for a dry gas seal at high pressures[J]. Tribology, 2014, 34(5): 543-552. [许静, 彭旭东, 白少先. 高压干气密封扭转变形结构因素影响分析[J]. 摩擦学学报, 2014, 34(5): 543-552.] |
| [14] |
顾永泉.机械密封实用技术[M].北京:机械工业出版社,2001.
|
| [15] |
Ding Xuexing. Fluid state analysis on flow field of gas seal with spiral groove based on CFD[J]. Journal of Drainage and Irrigation Machinery Engineering, 2010, 28(4): 330-334. [丁雪兴. 基于CFD的螺旋槽干气密封端面流场流态分析[J]. 排灌机械工程学报, 2010, 28(4): 330-334.] |
| [16] |
Jiang Lin.Design of new type of groove and investgation of thermal-fouid-structure coupling for high pressure dry gas seal[D].Chengdu:Sichuan University,2014. [蒋琳.高压干气密封新型槽型设计及流-固-热耦合研究[D].成都:四川大学,2014.]
|
| [17] |
陆志良.空气动力学[M].北京:北京航空航天大学出版社,2009.
|
| [18] |
Pinkus O,Sterlicht B.流体动力润滑理论[M].西安交通大学轴承研究小组,译.北京:机械工业出版社,1980:1–26.
|
| [19] |
Li Jinhui.Study on mechanism for filming and failure of viscoplastic fluid hydrodynamic lubrication[D].Beijing:Beijing University of Technology,2013. [李锦辉.黏塑性流体动力润滑成膜及失效机理研究[D].北京:北京工业大学,2013.] http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2448029
|
 2018, Vol. 50
2018, Vol. 50

