由于受到地形地质等因素限制，岸边溢洪道的平面轴线需要被转弯一定角度设置为曲线型，内部水流成为了弯道水流。弯道水流的水面在凹岸壅高凸岸降低，产生横比降，凹岸形成明显的超高水位 $\Delta H$ ^[1–2]，见图1所示。但是当来流为高弗劳德数Fr、大流速的急流时，进入弯道的水体能量更加集中，直接冲击凹岸后形成严重超高水位，凸岸甚至出现底板露底。目前，绝大多数工程措施主要针对凹岸水位超高的不良水力现象，比如：渠底超高法、复合曲线法、斜槛法、盖板法和多级跌水消能法等^[3]。对于采取工程措施消除凸岸露底现象的较少涉及。因此，提出一种新型溢洪道形式，即曲线型局部超高阶梯溢洪道。

图1(Fig. 1)

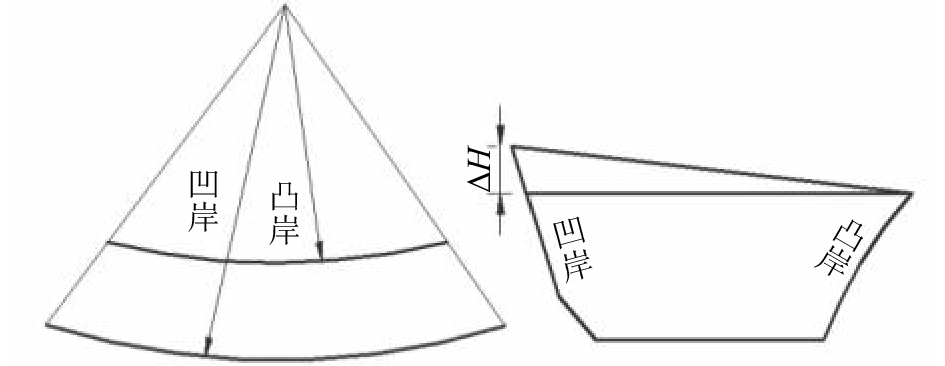图1 弯道超高示意 Fig. 1 Profile of super elevation in bend

曲线型溢洪道（弯道）的水流特性、不良流态的改善措施研究主要借助模型试验和数值模拟等方法。马淼等^[4]采用声学多普勒测速仪（ADV）试验研究了小宽深比条件下的弯道水流特性。周星等^[5]基于某核电站厂区山洪消能工程，采用试验研究了斜槛法在山区弯道河流消能设计中的应用。马晓等^[6]结合模型试验与3维数值模拟研究了盖板对泄洪隧道急流弯道水力特性的影响。

在溢洪道内布置阶梯后，阶梯的减速消能、改善流态的效果比较明显，钟晓凤^[7]、徐鹏^[8]等结合实际工程进行了详细阐述。丁明涛^[9]、周斌^[10]等则研究了渠底高程抬高后，能较为显著的平衡或减小离心力，以及降低横向水面差等。鉴于此，文中将阶梯和渠底超高融合形成新的溢洪道形式，并通过水工模型试验验证该类型溢洪道在工程中的可行性，采用数值模拟方法进一步研究横断面、沿程流速分布、压力分布和能量耗散率等水力学特性。

由于地形的限制，某水库的岸边溢洪道需要布置为曲线型，平面布置见图2（a）所示，横断面方向为 $x$ 轴，沿程方向为 $y$ 轴，沿水深方向为 ${\textit{z}}$ 轴。溢洪道由进水渠、控制段、泄槽、消能段组成。其中泄槽全长212.74 m，底坡为1∶3.5；平面缩窄段由14 m缩窄至10 m，收缩角为1.35°；平面转弯段的转弯半径为150 m，转弯角度为33.85°；泄槽后段的宽度为10 m。物理模型试验采用比尺1∶40的正态模型，最大下泄流量448 m³/s，最大下泄水头518.36 m，最大单宽流量44.8 m²/s。通过水平光滑曲线溢洪道的试验研究表明，当来流为高弗劳德数Fr时，泄槽转弯段和后段的凸岸底板出现了露底现象，入消力池的水流流速高，流态恶劣，见图3（a）所示（由于篇幅的原因，仅提供了工况为272 m³/s的成果）。

图2(Fig. 2)

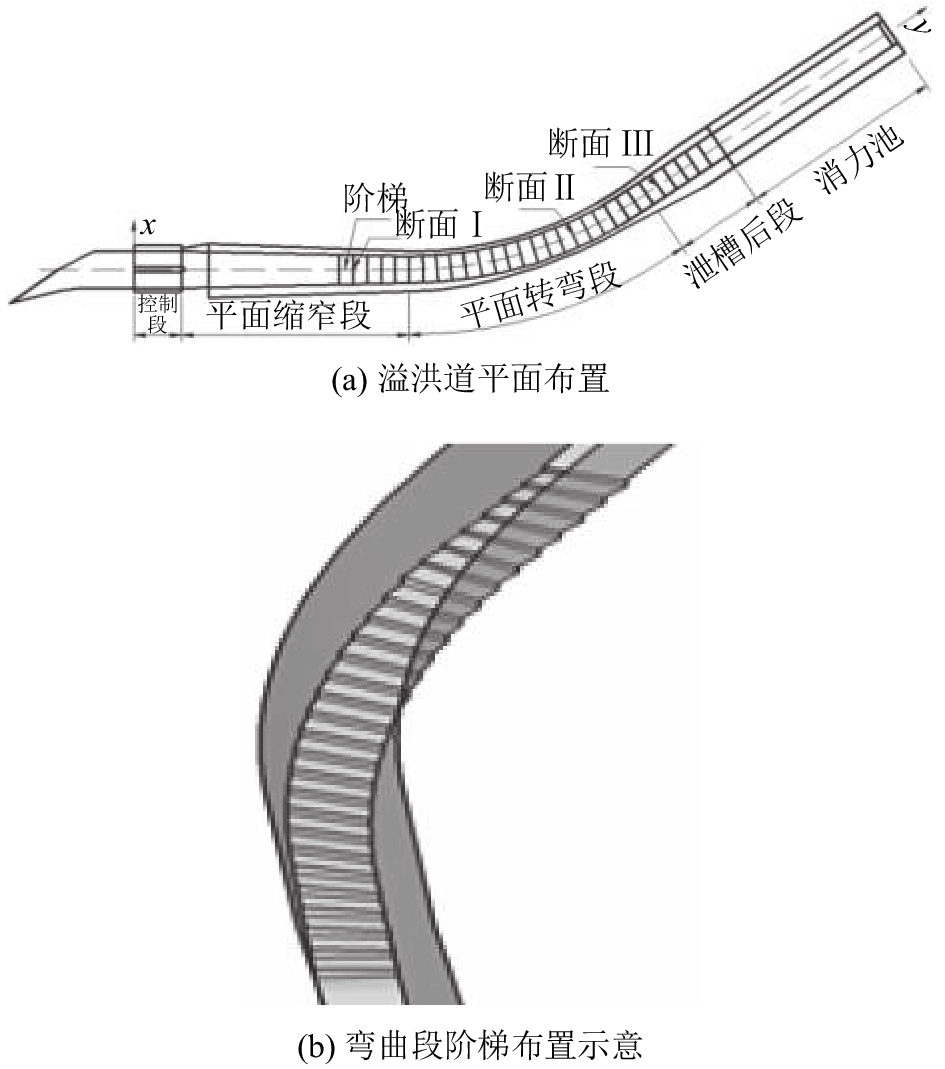图2 曲线阶梯溢洪道平面示意图 Fig. 2 Scheme of the stepped spillway

图3(Fig. 3)

图3 溢洪道转弯段流态 Fig. 3 Flow patterns at the bend section of the spillway

为此，采用了曲线型局部超高阶梯溢洪道，每级阶梯的凹岸和凸岸底板高程不同，且凹岸高于凸岸，以平衡弯曲段的离心力和减缓入池流速，断面示意见图4所示，图中 ${H_0}$ ～ ${H_3}$ 为底板高程，满足式（1）和（2）的要求。

图4(Fig. 4)

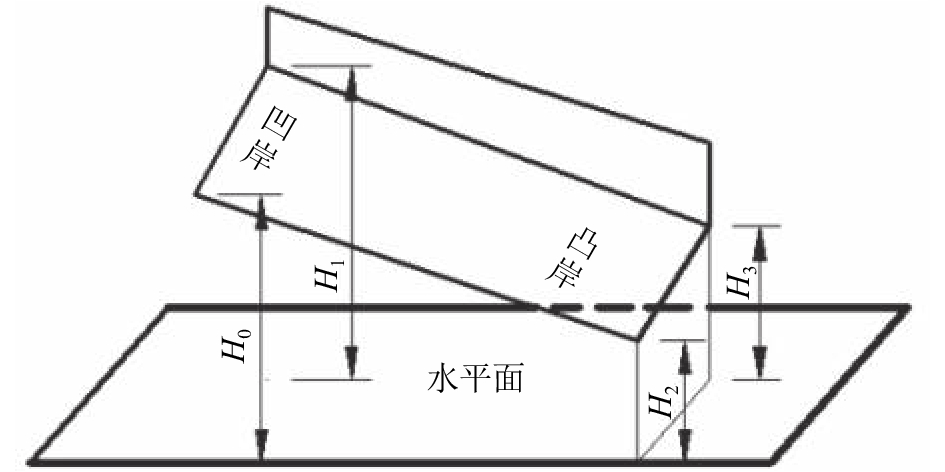图4 局部超高阶梯断面型式 Fig. 4 Profile of stepped section

虽然阶梯溢洪道具有消能率高、稳定入池流态等优点，但是在阶梯竖直面上部的负压较大，容易发生空化，尤其在大单宽流量时底部掺气浓度很低，可能遭受空蚀破坏^[11]。因此，在转弯段前设置了掺气坎。图3（b）为采用了前置掺气坎的曲线型局部超高阶梯溢洪道内的水流流态。从图中可以看出，底板露底现象被消除，沿程水流掺气充分，进入消力池的流态平稳。

由于物理模型试验难以捕捉复杂水流的细节信息，为了更加直观全面的了解该溢洪道的水力学特性，借助数值模拟方法进一步研究，并与水平光滑曲线溢洪道进行了比较分析。

曲线型局部阶梯溢洪道的水流是带有自由水面的3维黏性不可压缩湍流，连续性方程和雷诺时均方程RANS能较好的模拟弯道内的水流，控制方程如式（3）、（4）：

式中， $\left\langle {\;} \right\rangle $ 为时间平均值， $\rho $ 为水的密度， ${x_i}$ 为笛卡尔坐标系的 $x$ 、 $y$ 、 ${\textit{z}}$ 轴， ${u_i}$ 为沿坐标轴方向流体的速度， $p$ 和 $v$ 分别为压强和运动黏性系数， ${u_i'u_j'}$ 为湍流切应力，采用RNG $k - \varepsilon $ 方程求解。

自由水面的追踪采用VOF方法，它严格遵循质量守恒原理，已被李玲^[12]、周勤^[13]等应用于水工建筑物内水流的自由水面模拟，且取得较好的结果，见式（5）。在式（5）中， $F$ 代表水在单元体中的体积分数， $F$ =1，单元体充满水； $F$ =0，单元体完全被空气占据；0< $F$ <1，部分为水，其余部分为气，水气交界面作为自由水面。

在计算域内采用非结构网格和结构网格相结合，阶梯附近局部加密网格；基于单元体控制体积离散控制方程，方程中的体积分数、动量和紊动能等的扩散项均采用二阶迎风格式，压力–速度的耦合求解运用PISO算法。水流入口边界条件采用平均速度 $V$ =21 m/s，水深 $H$ =1.29 m；空气进口边界条件为相对压强，参考压强为标准大气压强；出口边界条件为压力出口，底板和边墙为光滑壁面，均采用无滑移固壁边界，黏性底层采用标准壁面函数处理。

在计算域内未设置前置掺气坎，让水流特性的仿真计算不受到掺气设施影响。初始的流场充满空气，以水深 $H$ 的水流流入，在ANSYS-FLUENT 14.0平台上实施溢洪道水气两相流的模拟计算。

为了验证数值模型的准确度，与转弯段沿程流速和水深分布的物理模型试验的结果进行了对比，如图5和6所示。

从图5可以看出，试验测量点的流速和计算值的最大误差为8.5%，满足要求。

在图6中，当水的体积分数 $F$ =0.55时，数值模拟计算的水面线和试验测量结果的吻合度良好。因此，VOF方法可以用来较为准确模拟自由水面的变化，且将体积分数 $F$ =0.55的水气交界面作为分析水深^[14]。经过以上分析认为建立的数值模型满足计算要求。

图5(Fig. 5)

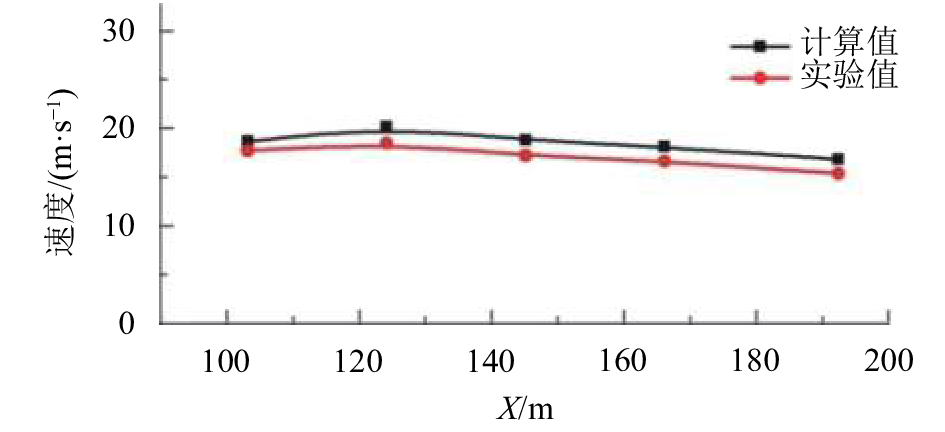图5 转弯段沿程流速对比 Fig. 5 Flow velocity for measured and calculated along spillway at the bend section

图6(Fig. 6)

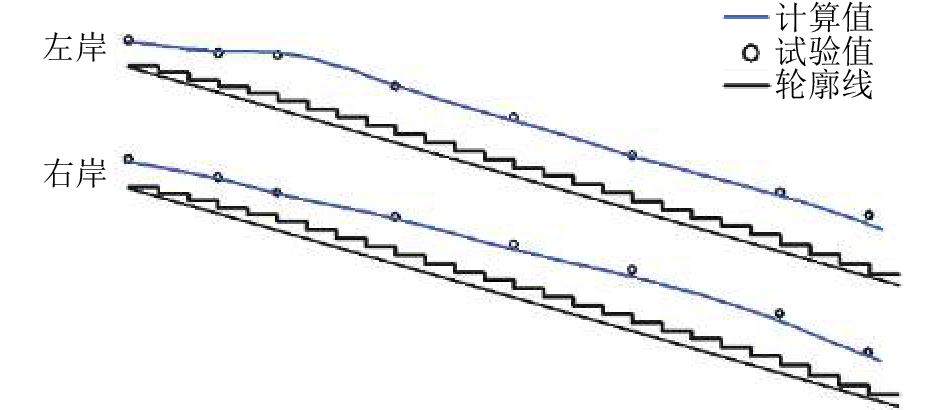图6 转弯段水面线对比 Fig. 6 Water surface for measured and calculated at the bend section

在转弯段布置多级阶梯，经过分析后选取了3个典型的横断面，分别为第一级阶梯尾端的进口断面Ⅰ、弯道中部的断面Ⅱ和转弯段最后一级阶梯尾端的出口断面Ⅲ，断面布置见图2（a）。通过横断面的流速分布判断主流区位置，见图7。

图7(Fig. 7)

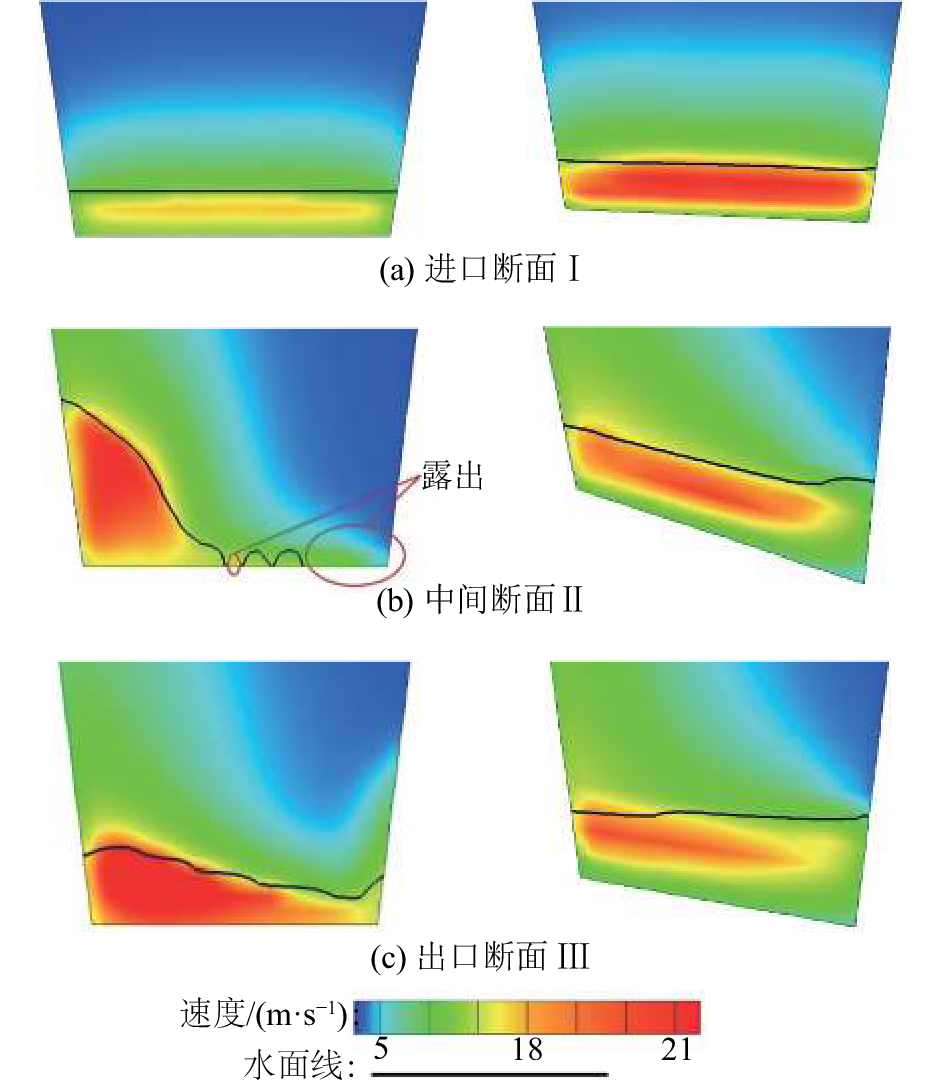图7 水平光滑（左）和局部超高阶梯溢洪道（右）的典型横断面流速分布 Fig. 7 Typical cross-sectioncal velocity distribution of horizontal smooth and local super-elevation step spillway

从图7（a）中可以看出，水平光滑曲线溢洪道进入转弯段流速低于局部超高阶梯溢洪道，这是由于阶梯的设置导致底部高程的变化，在阶梯处水流会形成滑移形态。在水流进入到弯道段后，苟兴智^[15]通过理论分析认为，由于离心力的作用将使凹岸水流从水面流向底板，进而导致水面壅高，给出了缓流下的自由水面超高方程。但在高弗劳德数Fr、急流条件下，水平光滑溢洪道的转弯水流直接冲击凹岸形成严重超高水体，主流区已经明显脱离了凸岸，集中于凹岸，甚至在凸岸底部出现露底，见图7（b）。

为了解决此不良水力现象，将阶梯凹岸底部高程抬高来平衡弯道急流的离心力，进而让横断面水深分布逐渐被调整，使得主流区分布均匀，见图7（b）中局部超高阶梯横断面流速分布。

从图7（c）中也可以看出，水平光滑溢洪道进入消力池的流速很大，达到26 m/s，主流区仍然严重偏离至凹岸；在布置阶梯后，入池流速为19 m/s，较大的减缓了入池流速，抬高凹岸底部高程后，主流区位置稍偏移至凹岸，但整体横向分布均匀。

通过分析主流区的位置可以发现，局部超高曲线型阶梯溢洪道较好的解决了底板露底和减缓了沿程流速，进入消力池的水流流态也得到明显改善。

鉴于溢洪道是曲线型的不规则形状，沿中轴线的曲面难以获取，故将弯道中部的断面Ⅱ的阶梯沿程和平台的流速矢量分布分别投影至 $Y{\textit{Z}}$ 平面和 $XY$ 平面，如图8所示。由于水平光滑溢洪道出现了露底，用其作为对比已经没有意义。因此，分析了局部超高阶梯溢洪道的流速矢量分布。

图8(Fig. 8)

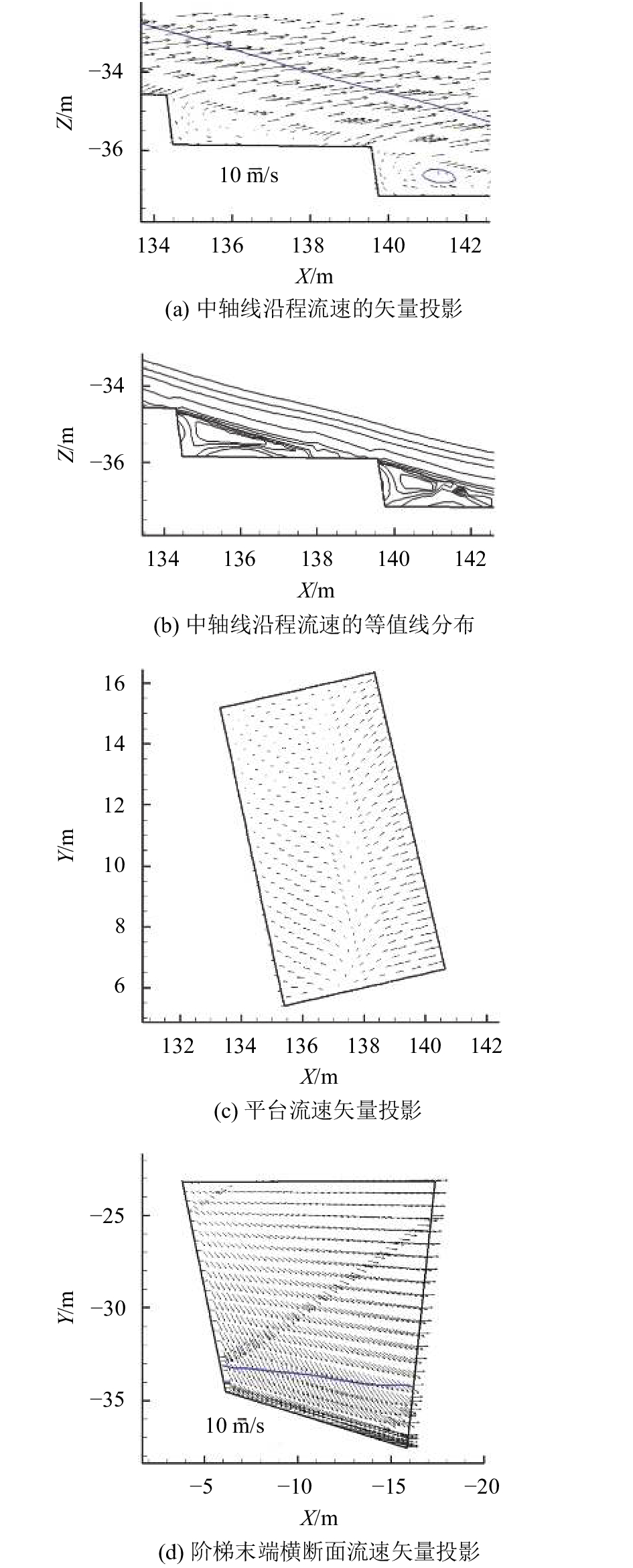图8 单级阶梯流速矢量分布 Fig. 8 Velocity distribution of a single stepped

图8（a）给出了沿程流速矢量和等值线分布，基本反映了阶梯附近的漩涡区和水流流态。阶梯溢流坝面上的水流流态可分为水舌跌落流和滑移流两种形式^[16]。

从图8（a）可以看出，水流呈现出滑移流流态，与程香菊等^[17]关于阶梯溢流坝水气两相流的研究结果一致。同时，在每个阶梯的竖立面和平台的三角区域内形成一个范围较宽且稳定的漩涡，水流相互产生剪切，形成动量交换和能量损失。

从图8（b）和图8（c）可以看出，抬高阶梯凹岸后，水流的径向作用加强，沿阶梯平台横向上有较大的流速，流向了凸岸，达到凸岸后被边墙偏转。分析流速分布后，发现弯道处的阶梯上形成了3维消能区域，与传统的阶梯2维消能区域相比，水体的能量耗散会被增强。

阶梯的压力分布规律能够初步预测溢洪道发生空蚀破坏的位置和概率，陈群等比较阶梯压力实测值和数值计算值后，发现两者分布规律近似，数值相差较小^[18]。图9为断面Ⅱ沿 $Y{\textit{Z}}$ 平面和 $XY$ 平面的单级阶梯压强等值线投影。

从图9中可以看出：在凹岸边墙的竖立面形成较大范围的负压区，最大负压值约为36 kPa，出现较大负压的原因在于竖立面和台阶的前缘区域内存在回流区，如图9（a）所示，且离心力和重力作用会使水流从水面流向底板，形成竖向水流，开始向主流方向偏转，使得回流区较为稳定，图8（d）清晰显示了主流偏转。在中轴线沿程的负压区位于竖立面的上部，最大负压值约为6.3 kPa，下部为正压区，延伸至平台，如图9（b）所示；由于水流的横向流动在凸岸被边墙折冲，结合流速分布和主流区位置可以看出凸岸边墙附近的流速较小，未有负压区，如图9（c）所示。

图9（d）更加直观揭示了底板压强从凹岸边墙至凸岸边墙的横向变化。从图9（d）中可知，阶梯负压值和范围从凹岸至凸岸逐渐减小，负压区域主要位于凹岸边墙、竖立面与台阶面的前缘三角区域，范围较小。

分析压力分布规律后，并依据空化数的定义式（6）可知存在负压的区域易发生空蚀空化。在曲线型溢洪道上布置局部超高阶梯，需要在转弯段的前部设置掺气措施，避免空蚀空化，在试验中已被证实。

图9(Fig. 9)

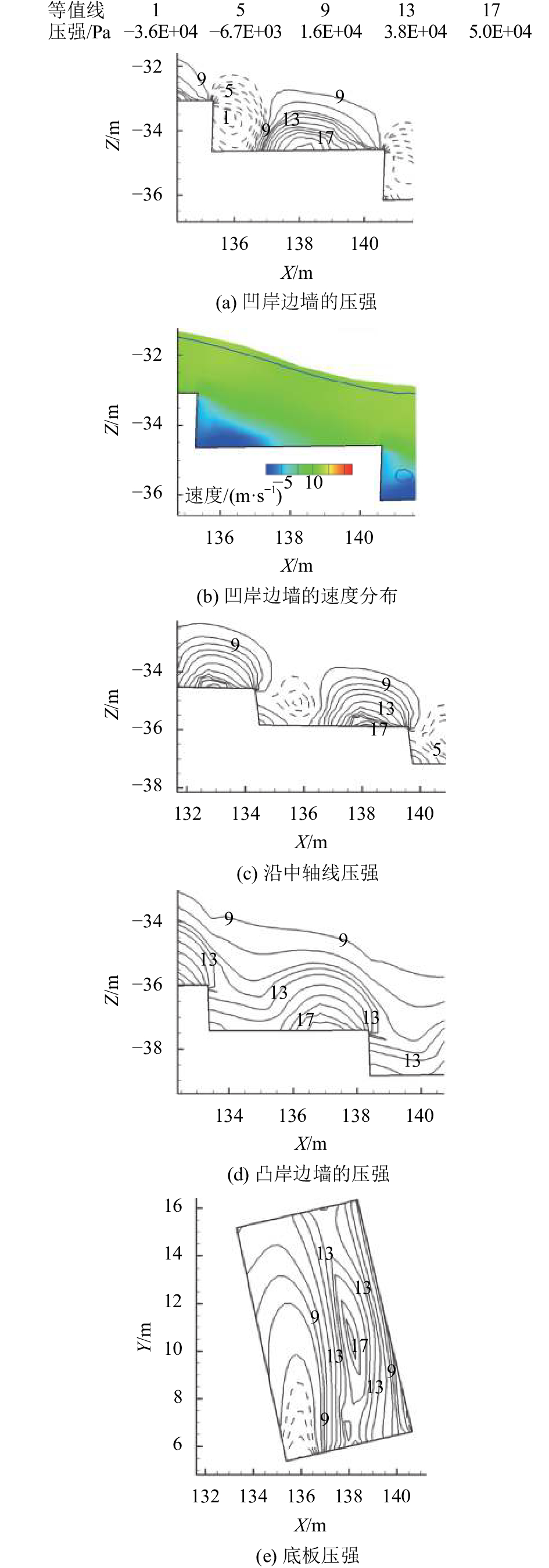图9 断面Ⅱ单级阶梯压强分布 Fig. 9 Pressure distribution of a single stepped at section Ⅱ

提出的局部曲线型超高阶梯溢洪道不仅要改变入消力池的流态，而且也要消耗掉沿程的水体能量，进而降低溢洪道衔接段和消力池的工程量。消能率指标可以判断能量的损失率，它依据能量守恒原理，基于沿程能量损失 $\Delta E$ 与上游总能量 ${E_{\rm a}}$ 之比计算，即：

式中： ${\rm a}$ 和 ${\rm b}$ 分别为曲线型溢洪道堰顶断面、转弯段出口断面； $E_{\rm a}$ 为堰顶总能量， ${E_{\rm a}} = {h_{\rm a}} + V_{\rm a}^2/2g$ ； ${E_{\rm b}}$ 为转弯段出口能量， ${E_{\rm b}} = {h_{\rm b}} + V_{\rm b}^2/2g$ ； ${V_{\rm a}}$ 、 ${V_{\rm b}}$ 为断面 ${\rm a}$ 和 ${\rm b}$ 处的平均流速， ${h_{\rm a}}$ 、 ${h_{\rm b}}$ 为断面 ${\rm a}$ 和 ${\rm b}$ 的水深。

比较分析水平光滑溢洪道和局部超高阶梯溢洪的消能率，计算后的消能率为15.11%和61.39%。因此，阶梯附近的漩涡损耗掉了部分能量，是主要的消能方式。对于局部超高阶梯，不仅沿程伴随纵向速度分量，而且在平台上也有横向速度分量，形成了各种尺度和强度的漩涡，水流被充分紊动，增加了沿程的消能率。

由于地形条件的限制，岸边溢洪道需要布置成曲线型。当来流为大流速、高弗劳德数Fr时，曲线型光滑溢洪在弯道段受到离心力的作用，会导致底板出现露底，入消力池水流流态恶劣。提出了在溢洪道上布置阶梯，消除沿程水体能量；同时，抬高凹岸每级阶梯底板高程，形成局部超高溢洪道，改善水流流态。通过物理模型试验验证了该溢洪道的运用，结合3维水动力学数值模型和VOF方法对比分析曲线型光滑溢洪道和局部超高阶梯溢洪道的水力学特性和消能特性，主要结论如下：

1）在阶梯凹岸底板高程局部抬高后，抵消了弯道离心力，使主流区沿横断面分布均匀，有效的避免了凸岸底板露底。

2）溢洪道内布置的阶梯，让阶梯尾部的漩涡区和横断面水流形成了3维消能区，与光滑溢洪道相比，沿程能量损失明显加强；但是，被抬高的凹岸附近会形成局部负压区，易导致空蚀空化，需要布置前置掺气坎。

3）在曲线型溢洪道内，布置局部超高阶梯能成功解决因流速大、弗劳德数高造成的底板露底，减缓沿程流速、增加沿程能量损失和改善入池水流流态，但是凹岸附近的压力值偏大。该形式溢洪道可为解决类似工程问题提供了一种全新的思路和方法。