多参加权分数阶傅里叶变换(multiple parameters weighted-type fractional Fourier transform,MP-WFRFT)是在WFRFT基础上提出的一种新型信号处理手段,可使基带星座产生模糊、裂变特性,在一定程度上能提升系统的抗截获性能,应用于保密通信之中[1–2]。WFRFT由Shih于1995年提出[3],因其具有良好的时频域分布特性[4]及参数设计灵活的特点,能与传统单载波(single carrier,SC)与多载波(multi-carrier,MC)载波体制相兼容,已成为载波体制发展中的一个重要研究方向[5]。文献[6–7]基于传统FRFT的数学理论推导指出WFRFT加权系数内含周期性,为MP-WFRFT变换特性进一步研究奠定了坚实基础;文献[8–9]以4QAM基带调制方式为例,对基于MP-WFRFT变换的基带星座裂变规律进行初步探索,分析了星座裂变的基本机制及可能的星座裂变图案,但对具体星座裂变点数及底层裂变机理仍不明确;文献[10–12]进一步探索在4QAM基带调制条件下,将MP-WFRFT与其他加密手段结合,以提升通信系统安全的可行性,但缺乏基于MP-WFRFT通信系统的定量参数设计及相应优化准则。此外,文献[8–12]都仅针对4QAM基带信号经MP-WFRFT处理后星座裂变成16QAM的基本情况进行了探索,对基带调制阶数大于4的情况并没有涉及。
基于此,作者拟对基于MP-WFRFT的8PSK基带星座裂变规律进行探究,通过对其时域、频域分量定性、定量分析,从向量合成角度建立星座裂变的几何分析模型,可实现时域分量星座点裂变规律的精确描述;结合频域分量类高斯噪声特性的定量研究,搭建基于MP-WFRFT的通信系统,并建立优化模型以实现最终的优化求解。
1 基本原理经典的4项WFRFT(4-WFRFT)只包含一个参数,即WFRFT调制阶数
| ${ F} = \frac{1}{{\sqrt N }}\left[ {\begin{array}{*{20}{c}} 1&1&1& \cdots &1 \\ 1&{{\xi ^{1 \cdot 1}}}&{{\xi ^{1 \cdot 2}}}& \cdots &{{\xi ^{1 \cdot (N - 1)}}} \\ 1&{{\xi ^{2 \cdot 1}}}&{{\xi ^{2 \cdot 2}}}& \cdots &{{\xi ^{2(N - 1)}}} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1&{{\xi ^{(N - 1) \cdot 1}}}&{{\xi ^{(N - 1) \cdot 2}}}& \cdots &{{\xi ^{(N - 1)(N - 1)}}} \end{array}} \right]$ | (1) |
式中,
| $\begin{aligned}[b] { W}_{{V}}^\alpha ({{{x}}_0}) = &{\omega _0}({{V}},\alpha ){{{x}}_0} + {\omega _1}({{V}},\alpha ){{{x}}_1} + \\ &{\omega _2}({{V}},\alpha ){{{x}}_2} + {\omega _3}({{V}},\alpha ){{{x}}_3}\end{aligned} $ | (2) |
式中:
| ${\omega _l}({{V}},\alpha ) = \frac{1}{4}\sum\limits_{k = 0}^3 {\exp \left\{ {\frac{{{\rm j}2{\text{π}}}}{4}\left[ {\alpha \left( {4{m_k} + 1} \right)\left( {4{n_k} + k} \right) - lk} \right]} \right\}} $ | (3) |
考虑到实际处理过程多以矩阵形式展开,且DFT矩阵具有如下特性:
| $ \begin{aligned}[b]{{W}}_{{V}}^\alpha ({{{x}}_0}) = & ({\omega _0}({{V}},\alpha ){{I}} + {\omega _1}({{V}},\alpha ){{F}} + \\& {\omega _2}({{V}},\alpha ){{P}} + {\omega _3}({{V}},\alpha ){{PF}}){{{x}}_0} \end{aligned} $ | (4) |
由式(4)可推导出基于MP-WFRFT的混合载波通信系统基本实现形式,其物理实现结构如图1所示[5]:
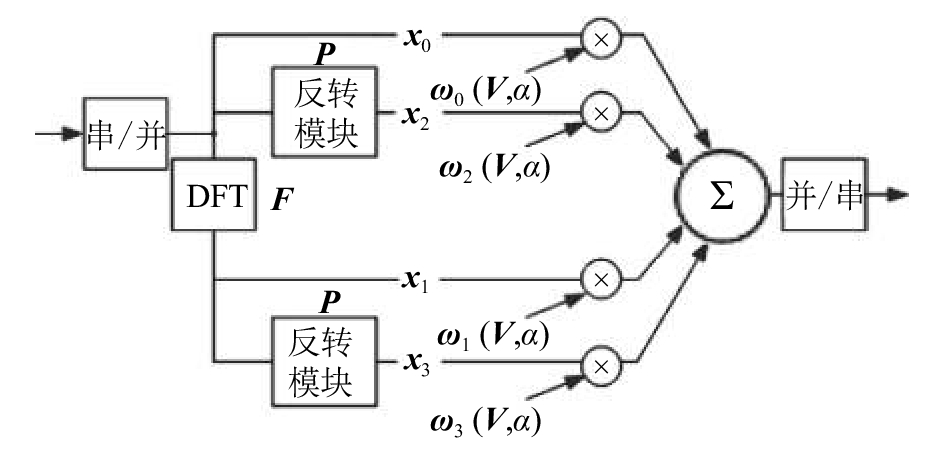 |
| 图1 基于MP-WFRFT系统物理实现框图 Fig. 1 Physical implementation of MP-WFRFT-based systems |
图1中,当
关于图1及式(4)展示的MP-WFRFT处理过程,目前主要开展如下两方面研究:从频域项(
式(4)中,
为更加直观地研究式(4)中时域组合项特性,定义星座裂变函数:
| $T_{{V}}^\alpha ({{{x}}_0}) = {\omega _0}({{V}},\alpha ){{{x}}_0} + {\omega _2}({{V}},\alpha ){{{x}}_2}$ | (5) |
式中,
一般而言,
由于本文以8PSK作为基带信号基本样式,当将
根据排列组合基本知识可推知此时最多可形成
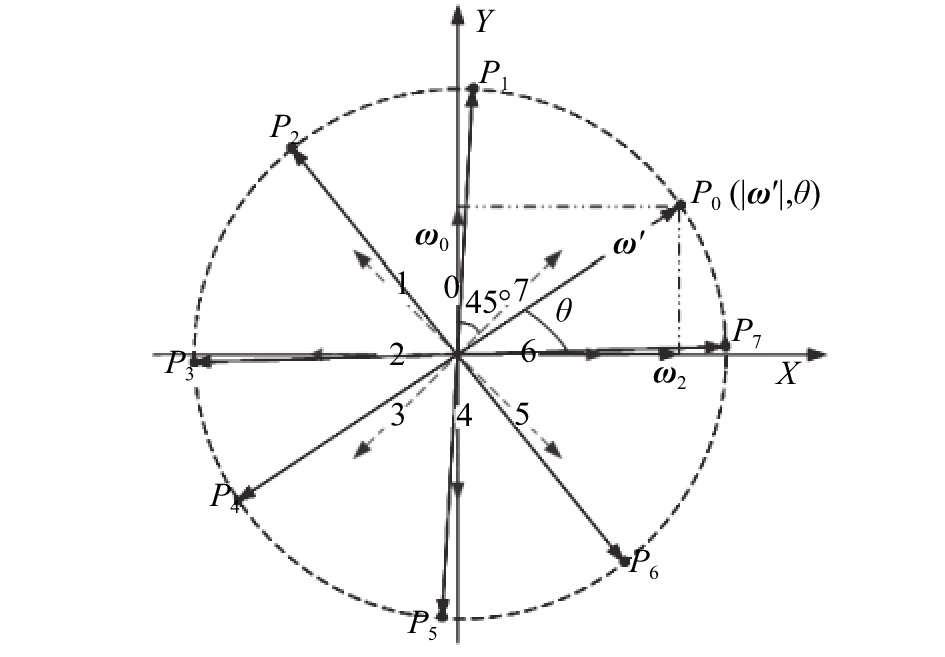 |
| 图2 基于MP-WFRFT的8PSK裂变几何模型 Fig. 2 Splitting geometry diagram of 8PSK in MP-WFRFT-based systems |
以分组1)为例,当
对于分组2)、3)、
此外,结合分组1)研究可知,形成的8个星座点所对应圆的半径为
如图3所示,
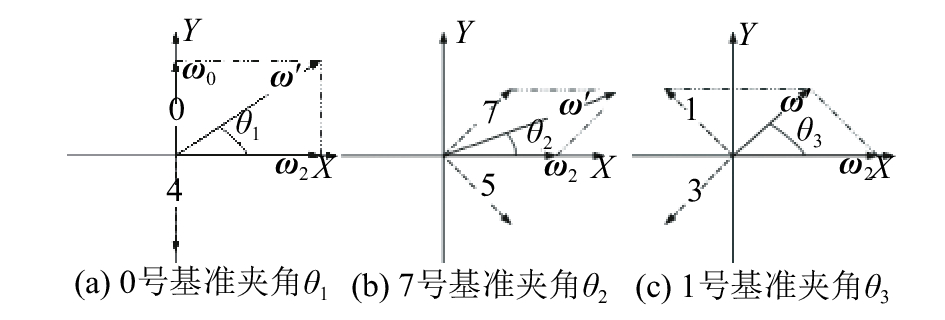 |
| 图3 合成向量与星座点重合关系分析 Fig. 3 Relationship between combined vector and constellation superposition |
同理对于图3(b),为满足星座重合的条件,
结合上述分析可知,当
通过第2节中关于8PSK星座裂变机理分析,搭建了基于MP-WFRFT的8PSK星座裂变系统,如图4所示。
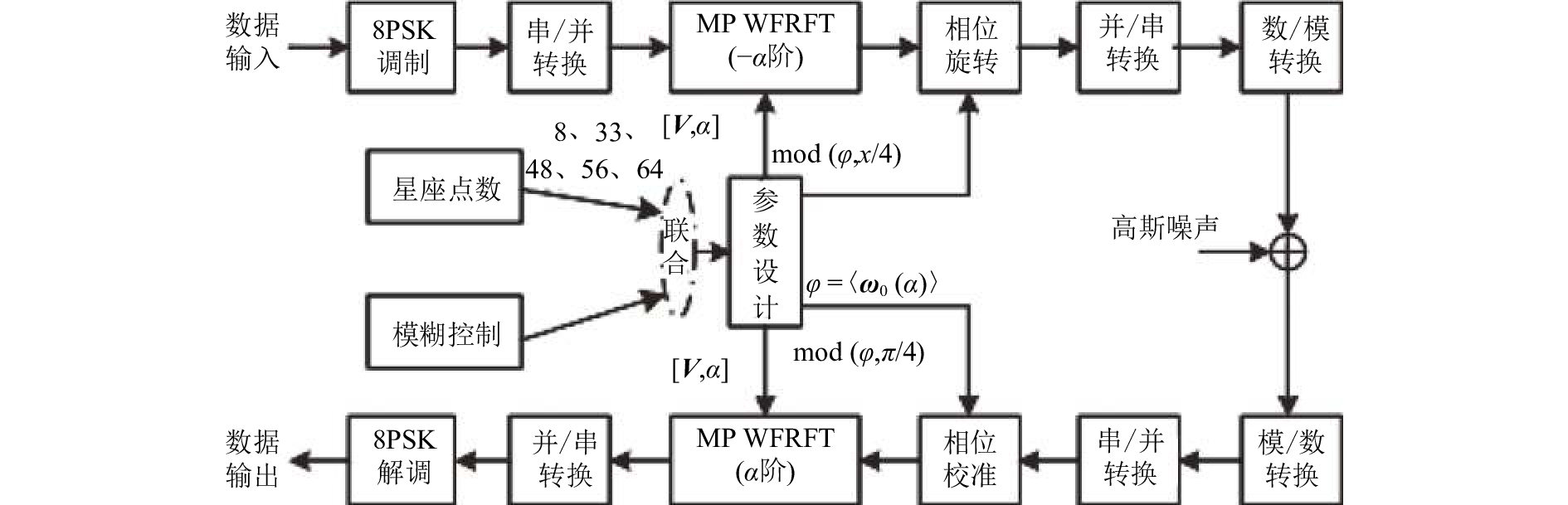 |
| 图4 基于MP-WFRFT星座裂变通信系统 Fig. 4 Constellation splitting systems based on MP-WFRFT |
在收发系统中,参数
为使图4中基于MP-WFRFT星座的裂变系统具有较好的保密通信性能,一方面通过设计合成星座点数(8、33、48、56、64点)进行星座伪装,另一方面通过模糊控制合理加入类高斯噪声,进而增强系统整体的抗截获性能。同时,根据第2节星座裂变分析可知模糊控制由式(4)中频域合成量
| $\left\{ \begin{array}{l} \min \;f({{V}},\alpha ) = \sqrt {{{\left| {\left| {{\omega _0}} \right| - \lambda \left| {{\omega _2}} \right|} \right|}^2}} , \\ {\rm s}.{\rm t}.\;\;\max \{ \left| {{\omega _1}} \right|,\left| {{\omega _3}} \right|\} < \delta ; \\ \;\;\;\;\;\;\left| {{\omega _0} \cdot {\omega _2}} \right| \le \varepsilon ; \\ \;\;\;\;\;\;{{V}}{\rm{ = [}}{{MV}}{\rm{,}}{{NV}}{\rm{];}} \\ \;\;\;\;\;{{MV}} = \left[ {{m_0},{m_1},{m_2},{m_3}} \right]; \\ \;\;\;\;\;{{NV}} = \left[ {{n_0},{n_1},{n_2},{n_3}} \right]; \\ \;\;\;\;\;\;0 \le {m_i}{\rm{,}}{n_i} \le U{\rm{,}}i{\rm{ = }}0{\rm{,}}1{\rm{,2,3;}}\; \\ \;\;\;\;\;\;\alpha \in [0,Q),Q \le 4 \\ \end{array} \right.$ | (6) |
式中:
根据第2节中图2、3星座裂变规律分析,结合式(6)中的优化模型,对基于MP-WFRFT的8PSK星座裂变进行仿真验证,并对相关通信性能进行测试。在本仿真中,设置整数取值边界
为更加清晰直观地验证图2~3中反映的星座裂变规律,对于式(6)中的模糊约束取值为
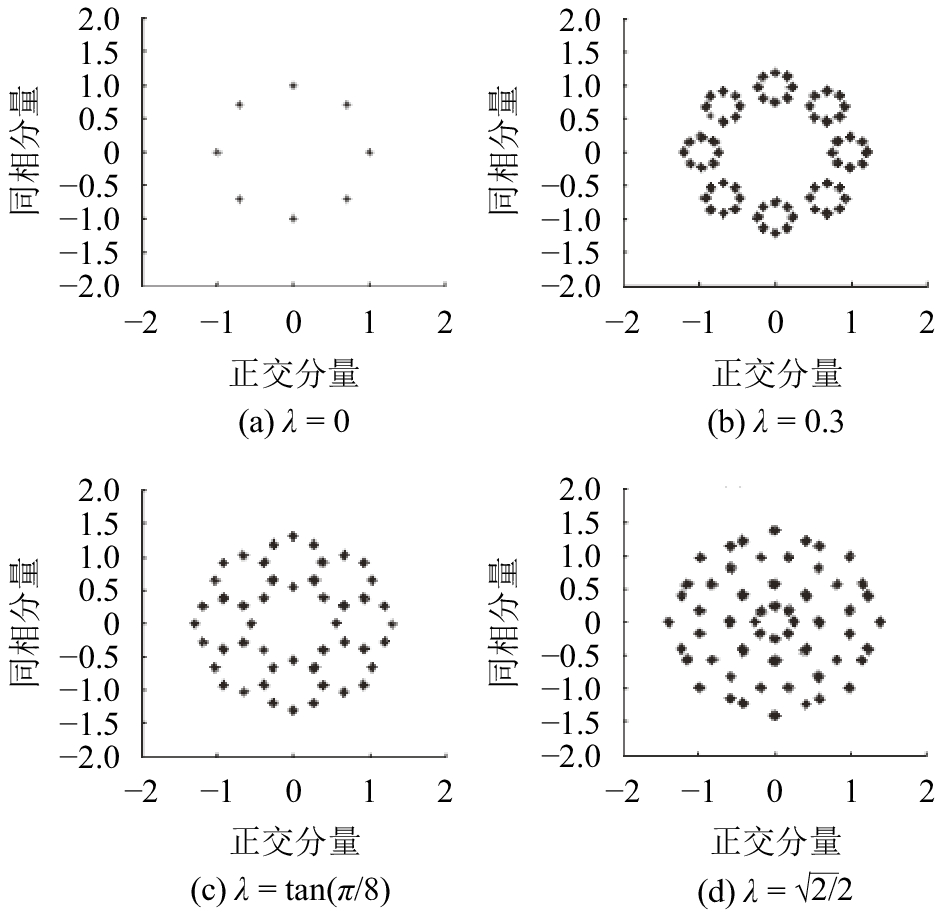 |
|
图5 不同
|
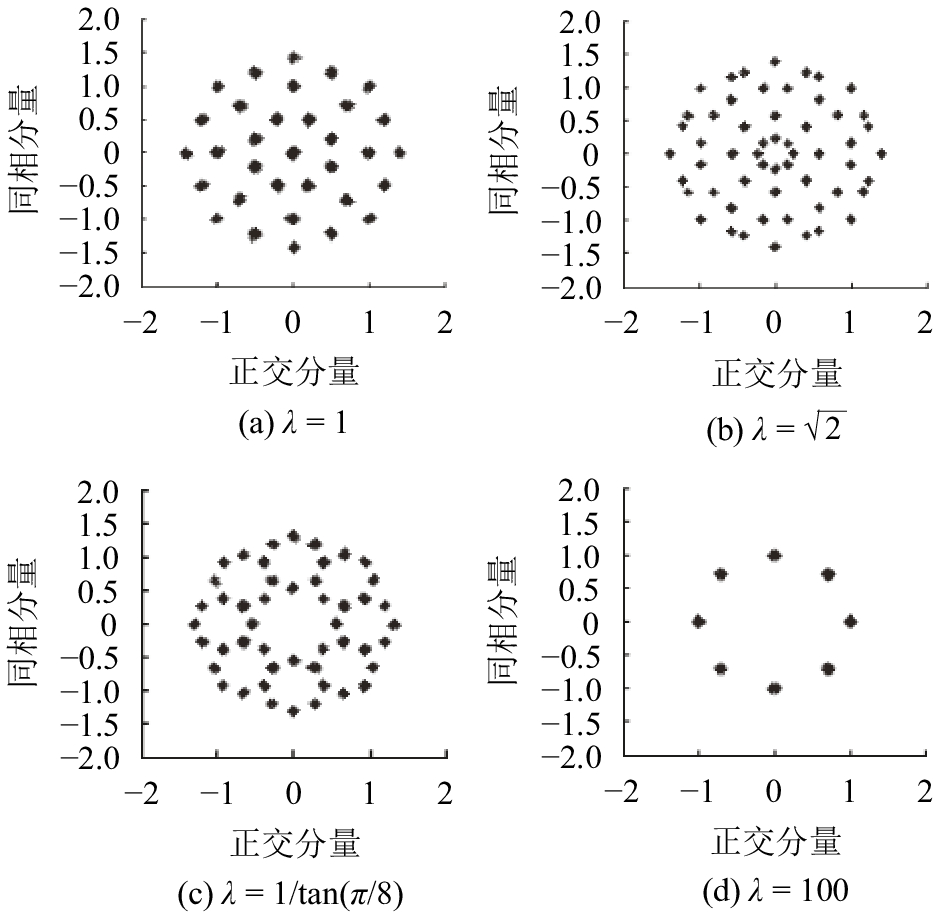 |
|
图6 不同
|
由图5~6可知,第2节推导得出的关于
对比观测图5~图6,可推出更为一般的结论:对于基于MP-WFRFT的8PSK基带星座裂变图样,星座点呈星形分布,且满足整体外圈星座点数多于内圈,这些都与APSK的星座设计准则相一致。同时,考虑到图2~3中基于MP-WFRFT基带星座裂变几何模型的一般性,对于其他PSK、QAM高阶基带信号具有相类似的分析思路,因而推之基于MP-WFRFT基带星座裂变图案具有类APSK的星形星座分布特性。
4.2 星座模糊特性为进一步分析模糊变量设计对星座裂变图案的影响,设定模糊约束取值为
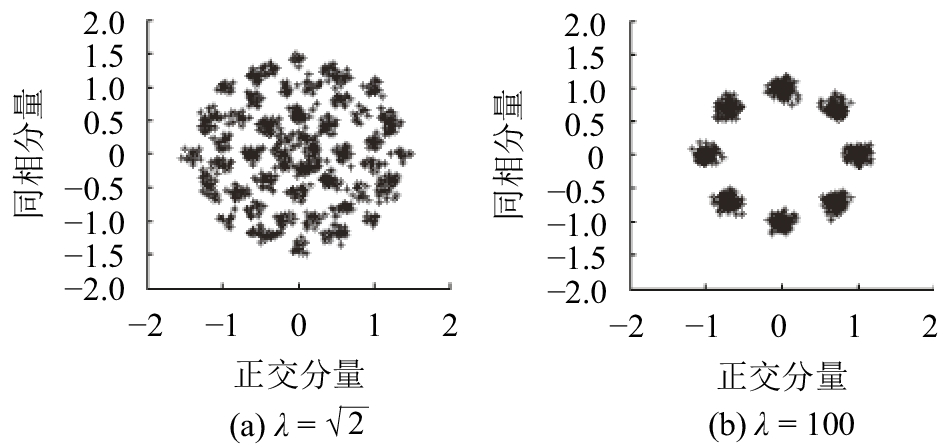 |
| 图7 星座模糊裂变合成效果 Fig. 7 Constellation splitting and blurring diagram |
对比图6与7,可以将图7(a)、(b)视为基于图6(b)、(d),增加了额外高斯噪声;当前场景下,实际信道噪声为0,这就体现了式(4)中频域分量表现出来的类高斯特性。进一步扩展,当模糊量控制在一定范围之内,可对星座进行有效高斯模糊保护,以提升其星座的抗能量检测性能。
4.3 抗截获性能为进一步说明基于MP-WFRFT的星座裂变实用性,对其自身通信性能与非授权方通信性能进行对比仿真测试。
对比图6、7可知,图6(d)、7(b)两种情况下导致的原始星座变化相对最小,因而本次抗截获测试选取这两种情况下的误比特率(bit error rate,BER)结果进行对比。由GA优化得到的图6(d)、7(b)对应的MP-WFRFT参数组为
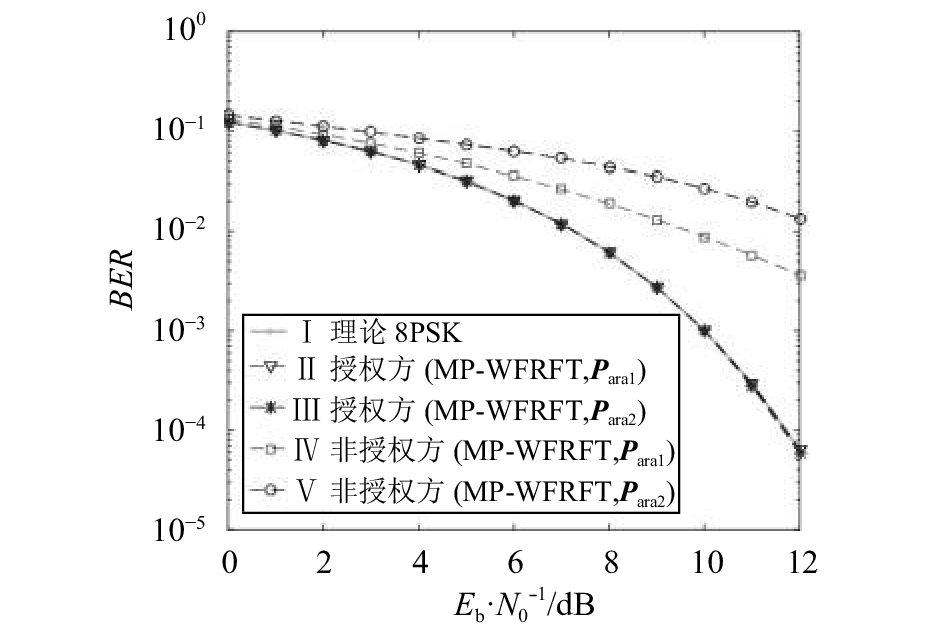 |
| 图8 不同通信场景下接收性能 Fig. 8 BER performances for different communication situations |
通过对比图8中曲线Ⅰ、Ⅱ、Ⅲ性能可知,对于参数组
由图6(d)、7(b)星座图可知,
对MP-WFRFT变换中的8PSK基带星座裂变进行了定性与定量分析,得出MP-WFRFT系数的模值比(
| [1] |
Ding B,Mei L,Sha X. Secure communication system based on alterable-parameter 4-weighted fractional Fourier transform[J]. Information Technology Journal, 2010, 9(1): 158-163. DOI:10.3923/itj.2010.158.163 |
| [2] |
Naznin L,Hossain M R,Ullah S E. Encrypted color image transmission in LDPC encoded MIMO wireless communication system with implementation of MP-WFRFT based[J]. Global Journal of Computer Science and Technology, 2017, 17(1): 27-38. |
| [3] |
Shih C C. Fractionalization of Fourier transform[J]. Optics Communications, 1995, 118(5): 495-498. |
| [4] |
Mei L,Sha X,Zhang N. The approach to carrier scheme convergence based on 4-weighted fractional Fourier transform[J]. IEEE Communications Letters, 2010, 14(6): 503-505. DOI:10.1109/LCOMM.2010.06.092413 |
| [5] |
Mei L,Sha X,Zhang Q,et al.The concepts of hybrid-carrier scheme communication system[C]//IEEE 6th International ICST Conference on Communications and Networking,Harbin:IEEE,2011:26–33.
|
| [6] |
Cariolaro G,Erseghe T,Kraniauskas P,et al. A unified framework for the fractional Fourier transforms[J]. IEEE Transactions on Signal Processing, 1998, 46(12): 3206-3219. DOI:10.1109/78.735297 |
| [7] |
Ran Q,Young D S,Tsang C C,et al. General multifractional Fourier transform method based on the generalized permutation matrix group[J]. IEEE Transactions on Signal Processing, 2005, 53(1): 83-98. DOI:10.1109/TSP.2004.837397 |
| [8] |
Mei Lin,Sha Xuejun,Zhang Naitong. Analysis of anti-scanning parameter ability and constellation splitting characteristic in weighted fractional Fourier transform system[J]. Journal of Yunnan University of Nationalities (Natural Sciences Edition), 2011, 20(5): 361-366. [梅林,沙学军,张乃通. 加权分数傅立叶变换通信系统抗参数扫描及星座分裂性能分析[J]. 云南民族大学学报(自然科学版), 2011, 20(5): 361-366. DOI:10.3969/j.issn.1672-8513.2011.05.011] |
| [9] |
Wang Shu,Da Xinyu,Chu Zhenyong,et al. Secure transmission for TDCS using 4-WFRFT and noise insertion[J]. Journal of Sichuan University (Engineering Science Edition), 2016, 48(3): 142-147. [王舒,达新宇,褚振勇,等. 采用4-WFRFT和人工噪声的变换域通信物理层安全传输[J]. 四川大学学报(工程科学版), 2016, 48(3): 142-147. DOI:10.15916/j.jsuese.2016.03.019] |
| [10] |
Da Xinyu, Lian Chen. Method of weighted Fourier transform domain communication[J]. Systems Engineering and Electronics, 2015, 37(12): 2853-2859. [达新宇,廉晨. 一种加权傅里叶变换域通信方法[J]. 系统工程与电子技术, 2015, 37(12): 2853-2859. DOI:10.3969/j.issn.1001-506X.2015.12.29] |
| [11] |
Fang X,Sha X,Li Y. MP-WFRFT and constellation scrambling based physical layer security system[J]. China Communications, 2016, 13(2): 138-145. |
| [12] |
Luo Z,Wang H,Zhou K,et al. Combined constellation rotation with weighted FRFT for secure transmission in polarization modulation based dual-polarized satellite communictions[J]. IEEE Access, 2017, 5: 27061-27073. DOI:10.1109/ACCESS.2017.2767678 |
| [13] |
Rao K R, Yip P.The transform and data compression handbook[M].Florida:CRC Press Inc,2001.
|
| [14] |
Lang J,Tao R,Ran Q,et al. The multiple-parameter fractional Fourier transform[J]. Science in China Series F:Information Sciences, 2008, 51(8): 1010-1024. DOI:10.1007/s11432-008-0073-6 |
| [15] |
Patzold M.Mobile fading channels[M].Hoboken:John Wiley & Sons Inc,2003.
|
| [16] |
Akmouche W.Detection of multicarrier modulations using 4th-order cumulants[C]//Proc IEEE MILCOM 1999,Atlantic:IEEE,1999:432–436.
|
| [17] |
Foster J D,Berry A M,Boland N,et al. Comparison of mixed-integer programming and genetic algorithm methods for distributed generation planning[J]. IEEE Transactions on Power Systems, 2014, 29(2): 833-843. DOI:10.1109/TPWRS.2013.2287880 |
| [18] |
Mei L,Zhang Q,Sha X,et al. WFRFT precoding for narrowband interference suppression in DFT-based block transmission systems[J]. IEEE Communications Letters, 2013, 17(10): 1916-1919. DOI:10.1109/LCOMM.2013.090213.131126 |
| [19] |
Fang X,Zhang N,Zhang S,et al. On physical layer security:Weighted fractional Fourier transform based user cooperation[J]. IEEE Transactions on Wireless Communications, 2017, 16(8): 5498-5510. DOI:10.1109/TWC.2017.2712158 |
 2018, Vol. 50
2018, Vol. 50


