2. 雅砻江流域水电开发有限公司,四川 成都 610051;
3. 四川大学 水力学与山区河流开发保护国家重点实验室,四川 成都 610065;
4. 四川大学 水利水电学院,四川 成都 610065
2. Yalong River Hydropower Development Co., Ltd., Chengdu 610051, China;
3. State Key Lab. of Hydraulics and Mountain River Eng., Sichuan Univ., Chengdu 610065, China;
4. College of Water Resources and Hydropower, Sichuan Univ., Chengdu 610065, China
岩石断裂力学的相关理论与试验研究成果在岩石工程、采矿工程和油气开采工程等领域获得了广泛关注[1–5]。陈建国等[1]通过测试龙马溪页岩的断裂韧性发现页岩中有机质(TOC)含量或黏土矿物越多,起裂后越容易向前延伸;宋晨鹏等[2]基于Griffith理论建立压裂裂缝与天然裂缝相遇后的延伸判别条件;任利等[3]基于断裂力学讨论了裂隙面摩擦系数、黏聚力、裂缝长度等因素对裂隙岩体压缩强度的影响规律;何思明等[4]基于岩石断裂力学确定了地震诱发岩体崩塌的力学机制影响因素;金衍等[5]建立了利用测井资料预测断裂韧性的理论模型,成功预测Ⅱ型断裂韧性连续值,并在压裂实践中得到验证。必须指出的是,实际岩石工程中,裂缝除承受纯Ⅰ型载荷外,还承受Ⅰ/Ⅱ复合型、Ⅱ型载荷。因此,开展岩石Ⅰ/Ⅱ拉剪复合断裂韧度测试及复合断裂行为的研究对讨论岩石工程稳定性和指导工程破岩均十分重要。
岩石断裂韧度动(静)态测试理论、技术及配套设备研制都是岩石断裂力学的核心研究内容且取得了丰富成果,有包括短圆棒(SR)试样、切槽三点弯曲圆棒(SECRBB)试样、人字形切槽三点弯曲圆棒(CB)试样、穿透直裂缝巴西圆盘(CSTBD)试样、人字形切槽巴西圆盘(CCNBD)试样及穿透直切槽半圆盘弯曲(SCB)试样等多种几何构形的试件用于岩石断裂韧度测试[6]。其中,国际岩石力学学会(ISRM)先后建议SR、CB、CCNBD和SCB这4种试样用于Ⅰ型静态断裂韧度测试。作者所在团队于2016年提出一种长宽比为2.0的切槽深梁试样(notched deep beam,NDB)用于岩石复合断裂测试[7],并利用有限元法对裂尖断裂参量进行了2、3维全方位数值标定[7–8];NDB试样配合三点弯曲试验可以进行纯Ⅰ型到纯Ⅱ型之间任意载荷复合度的拉剪断裂韧度测试。采用上述CSTBD和SCB等试件[9–10],国内外学者开展了大量的岩石复合断裂试验,获得了不同岩石在不同加载条件下的裂纹扩展路径与断裂强度。同时,利用试验结果与部分断裂准则进行了详细对比,进一步强化了断裂准则在岩石力学中的应用;相关结果也表明,岩石Ⅱ型断裂韧度与Ⅰ型断裂韧度的比值一般小于1。
相较于业界对岩石复合断裂强度及裂缝扩展路径问题的充分认识,国内外学者对复合加载下岩石断裂形成的破裂面及内在断裂机制却少有讨论和研究。传统固体力学假定材料是均匀的,但岩石是典型的多孔介质材料,内部存在形状、尺寸不一的微观裂缝、空隙等缺陷[11]。同时,岩石也是典型的晶体颗粒材料,宏观断裂起始于微观上的穿晶断裂、沿晶断裂及二者的耦合断裂模式。正因为岩石材料的微观结构特征,其断裂形成的破坏面不是完全光滑,浅丘、沟壑等总是存在于岩石断口表面[11]。因此,对岩石断口微观特征的研究有助于理解岩石微观破坏机理。在深部油气开采等领域,对复合载荷作用下形成的断裂面的研究也有助于认识压裂过程中流体与固体裂缝面的耦合机制。此外,谢和平等[12–13]认为岩石断口不规则性对岩石断裂韧度也存在影响。因此,有必要对复合载荷作用下形成的岩石断面进行细致刻画。Al-Shayea[10]利用扫描电镜放大1 000倍在微米尺度下对灰岩CSTBD试样复合断裂形成的粗糙面进行了研究,认为在微观尺寸下载荷复合度影响岩石断面的形貌特征。
基于砂岩复合断裂试验,探讨了岩石复合断裂强度特征,进一步利用LPM获取复合加载下的砂岩复合断面形貌,采用分形理论定量刻画了岩石复合断裂面的几何特征,总结并阐明了岩石在拉剪复合载荷作用下的内在断裂机制。
1 基于NDB试样的砂岩复合断裂韧度测试 1.1 NDB试样图1为对称三点弯曲加载下的NDB试样[7]。支座间距为
 |
| 图1 单边切槽深梁试样 Fig. 1 NDB specimen |
当裂缝与压缩载荷
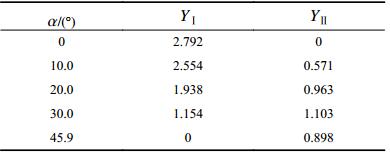
| ${K_{\text{Ⅰ}}} = \frac{{P\sqrt {{\text{π}} a} }}{{2WB}}{Y_{\rm I}}\left( {\frac{a}{W},\frac{S}{W},\alpha } \right)$ | (1) |
| ${K_{\text{Ⅱ}}} = \frac{{P\sqrt {{\text{π}} a} }}{{2WB}}{Y_{{\rm I}{\rm I}}}\left( {\frac{a}{W},\frac{S}{W},\alpha } \right)$ | (2) |
式中,
NDB试样几何尺寸为长180 mm,宽90 mm,厚76 mm;预制裂缝长度
 |
| 图2 砂岩NDB试样破坏模式 Fig. 2 Failure patterns of NDB specimens |
Lim等[15]统计分析了不同载荷复合度加载下SCB试样破裂路径问题,发现部分试样裂缝不从尖端起裂或一侧从尖端起裂而背侧不从尖端起裂;进一步观察了SCB试件破坏形成的断裂面,指出裂缝前沿前进时并非处于一个平面,认为这可能导致裂缝起裂位置不在尖端。然而,得益于较高的试件加工质量,从图2所示的砂岩NDB试样在不同载荷条件下的破坏均是从尖端开始起裂,并扩展至加载点。另外,从图2还可以看出,纯Ⅰ型断裂时裂缝沿初始裂缝平面扩展,随着裂缝倾角
根据式(1)和(2),利用峰值载荷
|
表1
|
 |
对于复合断裂,有学者使用基于最大能量释放率理论建立的有效应力强度因子以估计断裂韧度的等效值[18],即
| ${K_{{\rm{eff}}}} = \sqrt {{K^2_{\text{Ⅰ}}}{\rm{ + }}K^2_{{\text{Ⅱ}}}}$ | (3) |
式(3)本质上即从原点到
| ${M_{\rm e}} = \frac{2}{{\text{π}} }{\tan ^{ - 1}}\frac{{{K_{\text{Ⅱ}}}}}{{{K_{\text{Ⅰ}}}}}$ | (4) |
显然,0≤
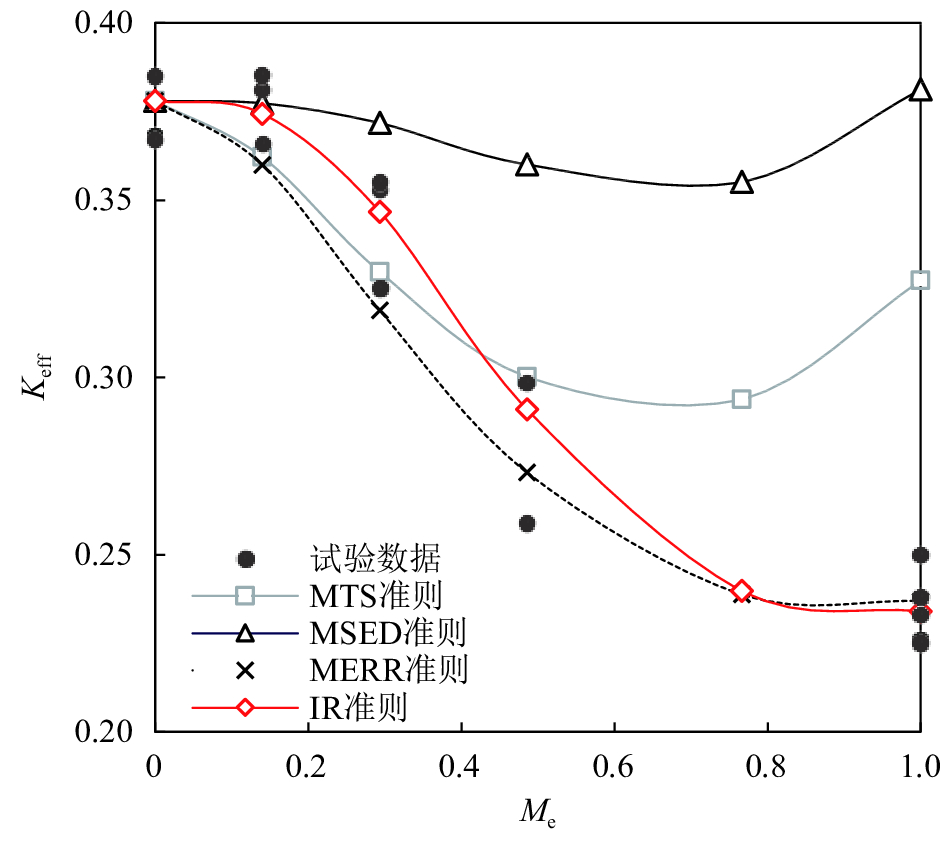
图3绘制了复合断裂韧度有效值与载荷复合度的关系。由图3可知,Ⅰ型和Ⅱ型断裂时的砂岩等效断裂韧度并不相等;随着载荷复合度增加,断裂韧度等效值逐步降低。进一步根据文献[18]中阐述的等效应力强度因子的物理含义,可知本文砂岩的临界最大能量释放率
 |
| 图3 复合断裂韧度等效值与载荷复合度的关系 Fig. 3 Plot of effective fracture toughness vs loading mixity |
图3中,
当
实际岩石工程中,总是希望一个可靠的断裂准则用于实时判断岩石裂缝是否已达到扩展条件及裂缝下一步扩展方向。目前,最为常用、最广为接受的3个复合断裂准则分别为最大切向应力(MTS)准则、最小应变能密度(MSED)因子准则和最大能量释放率(MERR)准则。针对弹脆性材料,作者也尝试性地提出改进的R(IR)准则以预测其复合断裂强度[16]。可以看出,IR准则与MERR准则可较好地预测砂岩的复合断裂强度;MTS和MSED准则严重高估了Ⅱ型为主的拉剪复合断裂。此外,作者也曾针对包括MTS、MSED和MERR等在内的线弹性断裂准则用于预测材料断裂强度的适用性进行了全面分析[24]。由于线弹性断裂力学无法准确定义裂纹尖端附近真实应力场[25],唯有假设一个核心区(根据不同模型、不同理论,核心区边界表达式可不同),在核心区内材料本构关系不清楚、也不关心(故线弹性断裂力学一般不精确描述和使用核心区材料本构模型),在核心区外假设材料为线弹性[25]。在这种理论假设下,利用应力强度因子和断裂韧度近似建立LEFM强度理论成为可能。也正是因为这样的假设,如果核心区边界为一个圆,该LEFM准则就难以准确估计岩石的复合断裂强度[9]。
3 砂岩复合断面的形貌特征与断裂机制 3.1 NDB试件断面扫描借助中国矿业大学(北京)煤炭资源与安全开采国家重点实验室的大尺度3维激光扫描仪对Ⅰ/Ⅱ复合断裂形成的砂岩断面形貌进行测量。采样间距设置为0.1 mm,由破坏后的NDB试件形态可知,复合加载条件下的破坏面长度并不一致,因此所有的试件均取从裂缝尖端到48 mm长范围内的数据进行重建及后续分析。在试件厚度方向,为了尽可能使用多的立方体尺寸覆盖粗糙面,也选择了中部48 mm的范围。因此,每一个试件用于形貌分析和重建的采样点数目为480
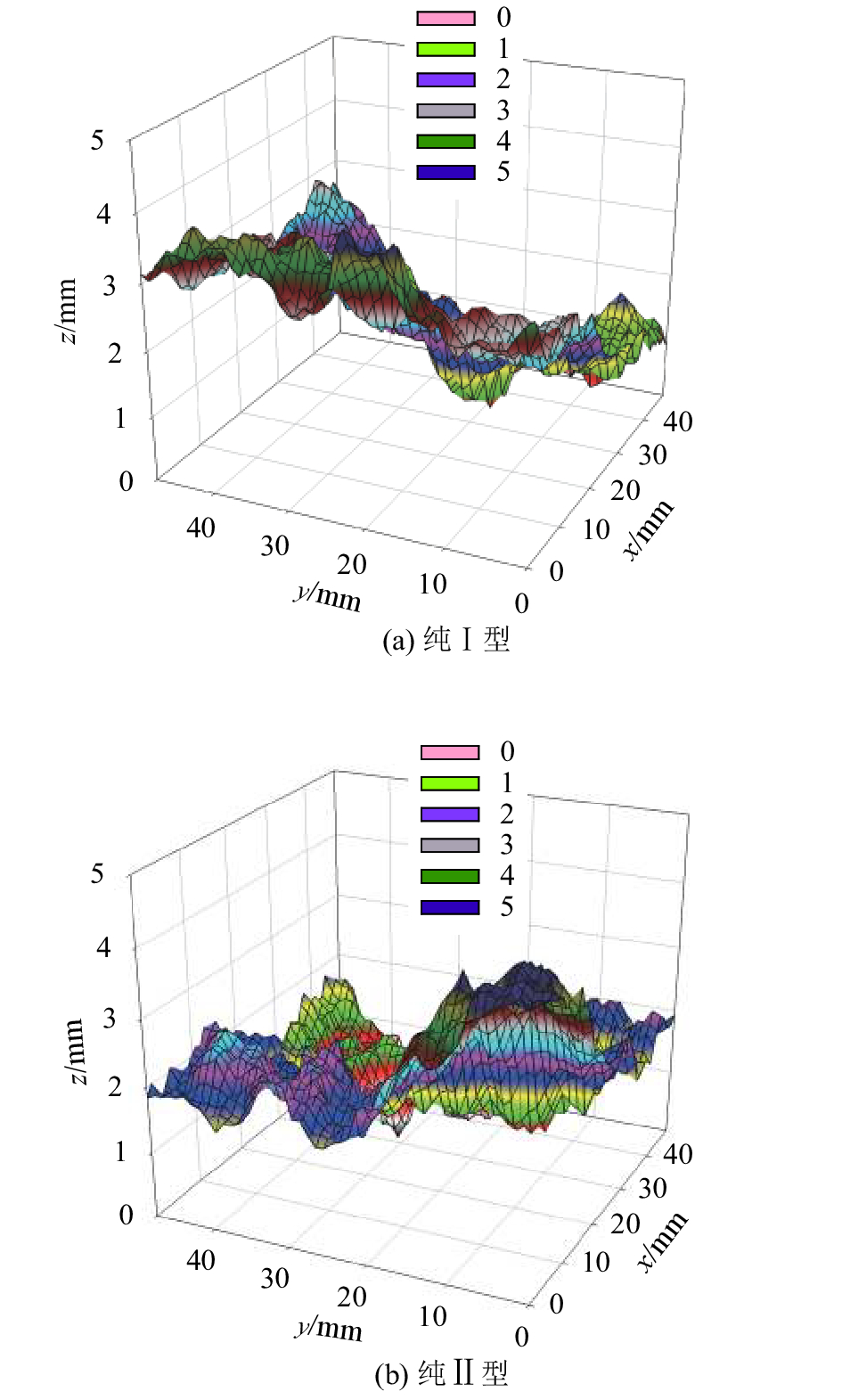 |
| 图4 纯Ⅰ型和纯Ⅱ型砂岩断面 Fig. 4 Mode Ⅰ and mode Ⅱ loadings induced fracture surfaces |
3.2 断面形貌特征分析
分形理论可定量刻画岩石断面的粗糙,利用立方体覆盖法对NDB试样断面形貌进行分析。表2列出了0~5号试件纯Ⅰ型断裂形成断口的覆盖结果。由表2可见,尺度
| 表2 0–5号试件断裂表面立方体覆盖结果 Tab. 2 Cubic covering results for sample 0–5 |
 |
分维计算结果表明每个角度的NDB试件破裂面均与0–5号试件断面有相似特征,即仅在一定观测尺度范围内有分形性质,结果见表3。
同时应注意到不同试件断面具有分形特征的尺度范围略有不同,这也是岩石断面区别于数学形貌的一个佐证,体现了岩石断面复杂性。整体上看,各NDB试件的断面在相应尺度内立方体数目和观测尺度在双对数坐标图中线性性质明显,相关系数
| 表3 NDB试件破裂面分形维数计算结果 Tab. 3 Fractal dimension results of NDB specimens’ surfaces |
 |
岩石断面的微观形貌与岩石微观结构有很大关系[26],考虑到试验所有砂岩全部来自同一个大石材,整体性质较为一致,故对比各NDB试件形貌具备可行性。纯Ⅰ型断裂形成的破裂面分维略小于复合载荷和纯Ⅱ型载荷导致的断裂面。也即,在Ⅰ/Ⅱ复合或纯Ⅱ型时,裂缝扩展过程中承受的剪切荷载对其断面形貌(尤其是微观形貌)有一定影响,且这种影响随着Ⅱ型载荷分量比例的增加略有轻微增加。考虑到试验误差,认为总体趋势上并没有表现出明显倾向性,也即在本文测试尺度范围内载荷复合度对断面的形成影响不大。值得注意的是,在更微观的尺寸观测粗糙面也许能反映更多不同,但全面考量粗糙面则应该用较大的尺度[27]。因此,需从砂岩微观破坏机理上理解粗糙度一致的现象。
3.3 砂岩复合断裂机制岩石微观断裂的3种类型(穿晶断裂、沿晶断裂和两者的组合断裂模式)中,由于晶体与晶体边界结合面相比晶体本身强度要弱,因而穿晶断裂需要消耗的能量更高。Zhang等[28]的对大理岩开展了系列动态断裂试验,结果表明:对于准静态加载下的岩石Ⅰ型断裂主要以沿晶破坏为主,穿晶破坏几乎不能观测到;随着加载速率提高,穿晶破坏变得越来越明显。注意到:图2中砂岩静态Ⅰ/Ⅱ复合断裂的破坏路径,裂缝沿初始断裂角
利用新近提出的NDB试样开展了脆性砂岩复合断裂测试,对其复合强度特征、断面形貌及断裂机制进行了详细探索,获得如下结论:
1)砂岩复合断裂有效断裂韧度从纯Ⅰ型到纯Ⅱ型逐步减小,且Ⅱ型与Ⅰ型断裂韧度比值为0.62,接近MERR准则的理论断裂韧度比。
2)IR准则与MERR准则可以较好地预测砂岩的复合断裂强度,而MTS和MSED准则严重高估了Ⅱ型为主的拉剪复合断裂。
3)对断面形貌进行定量刻画结果表明,砂岩在拉剪复合载荷作用下形成的断面形貌特征总体趋势上并没有表现出明显的倾向性,也即在本文测试尺度范围内拉剪载荷复合度对断面的形成没有影响。
4)拉剪载荷作用下,甚至Ⅱ型剪切载荷作用下,岩石内在断裂机制均为拉破坏。
| [1] |
Chen Jianguo,Deng Jingen,Yuan Junliang,et al. Research on the determination of type Ⅰ and Ⅱ of shale formation fracture toughness[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(6): 1101-1105. [陈建国,邓金根,袁俊亮,等. 页岩储层Ⅰ,Ⅱ型断裂韧性评价方法研究[J]. 岩石力学与工程学报, 2015, 34(6): 1101-1105.] |
| [2] |
Song Chenpeng,Lu Yiyu,Xia Binwei,et al. Effects of natural fractures on hydraulic fractures propagation of coal seams[J]. Journal of Northeastern University(Natural Science), 2013, 35(5): 756-760. [宋晨鹏,卢义玉,夏彬伟,等. 天然裂缝对煤层水力压裂裂缝扩展的影响[J]. 东北大学学报 (自然科学版), 2013, 35(5): 756-760.] |
| [3] |
Ren Li,Xie Heping,Xie Lingzhi,et al. Preliminary study on strength of cracked rock specimen based on fracture mechanics[J]. Engineering Mechanics, 2012, 30(2): 156-162. [任利,谢和平,谢凌志,等. 基于断裂力学的裂隙岩体强度分析初探[J]. 工程力学, 2012, 30(2): 156-162.] |
| [4] |
He Siming,Wu Yong,Li Xinpo.Collapse mechanism of danger rock triggered by earthquake[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(Supp 1):3359–3363. 何思明,吴永,李新坡.地震诱发岩体崩塌的力学机制[J].岩石力学与工程学报,2010,29(增1):3359–3363. |
| [5] |
Jin Yan,Chen Mian,Wang Huaiying,et al.Study on prediction method of fracture toughness of rock mode II by logging data[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(Supp 2):3630–3635. 金衍,陈勉,王怀英,等.利用测井资料预测岩石 Ⅱ 型断裂韧性的方法研究[J].岩石力学与工程学报,2008,27(增2):3630–3635. |
| [6] |
Backers T.Fracture toughness determination and micromechanics of rock under Mode Ⅰ and Mode Ⅱ loading[D].Potsdam:University of Potsdam,2005.
|
| [7] |
Luo Yi,Ren Li,Xie Lingzhi,et al.Single edge notched deep beam specimen to test Ⅰ/Ⅱ mixed-mode fracture toughness of rock:Numerical analysis and calibration[J].Chinese Journal of Rock Mechanics and Engineering,2016,35(Supp 2):3633–3643. 罗毅,任利,谢凌志,等.岩石Ⅰ/Ⅱ复合断裂韧度测试的单边切槽深梁试件:数值分析与标定[J].岩石力学与工程学报,2016,35(增2):3633–3643. |
| [8] |
Sun Xin,Zhu Zheming,Xie Lingzhi,et al. Investigation on mixed-mode fracture behavior of sand stone using a SENDB specimen[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(12): 2884-2894. [孙欣,朱哲明,谢凌志,等. 基于SENDB试样的砂岩复合脆性断裂行为研究[J]. 岩石力学与工程学报, 2017, 36(12): 2884-2894.] |
| [9] |
Ren L,Xie L Z,Xie H P,et al. Mixed-mode fracture behavior and related surface topography feature of a typical sandstone[J]. Rock Mechanics and Rock Engineering, 2016, 49(8): 3137-3153. DOI:10.1007/s00603-016-0959-3 |
| [10] |
Al-Shayea N A. Crack propagation trajectories for rocks under mixed mode Ⅰ-Ⅱ fracture[J]. Engineering Geology, 2005, 81(1): 84-97. DOI:10.1016/j.enggeo.2005.07.013 |
| [11] |
Ai T,Zhang R,Zhou H,et al. Box-counting methods to directly estimate the fractal dimension of a rock surface[J]. Applied Surface Science, 2014, 314: 610-621. DOI:10.1016/j.apsusc.2014.06.152 |
| [12] |
Xie Heping. Fractal geometry and its application to rock and soil materials[J]. Chinese Journal of Geotechnical Engineering, 1992, 14(1): 14-24. [谢和平. 分形几何及其在岩土力学中的应用[J]. 岩土工程学报, 1992, 14(1): 14-24. DOI:10.3321/j.issn:1000-4548.1992.01.002] |
| [13] |
Xie Heping,Chen Zhida. Fractal geometry and fracture of rock[J]. Acta Mechanica Sinica, 1988, 20(3): 264-271. [谢和平,陈至达. 分形几何与岩石断裂[J]. 力学学报, 1988, 20(3): 264-271.] |
| [14] |
Kuruppu M D,Obara Y,Ayatollahi M R,et al. ISRM-suggested method for determining the mode Ⅰ static fracture toughness using semi-circular bend specimen[J]. Rock Mechanics and Rock Engineering, 2014, 47(1): 267-274. DOI:10.1007/s00603-013-0422-7 |
| [15] |
Lim I L,Johnston I W,Choi S K,et al. Fracture testing of a soft rock with semi-circular specimens under three-point bending.Part 2-mixed-mode[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1994, 31(3): 199-212. |
| [16] |
Ren L,Zhu Z,Wang M,et al. Mixed-mode elastic-plastic fractures:Improved R-criterion[J]. Journal of Engineering Mechanics, 2014, 140(6): 04014033. DOI:10.1061/(ASCE)EM.1943-7889.0000755 |
| [17] |
Ayatollahi M,Akbardoost J. Size effects in mode Ⅱ brittle fracture of rocks[J]. Engineering Fracture Mechanics, 2013, 112/113: 165-180. DOI:10.1016/j.engfracmech.2013.10.011 |
| [18] |
Aliha M,Behbahani H,Fazaeli H,et al. Study of characteristic specification on mixed mode fracture toughness of asphalt mixtures[J]. Construction and Building Materials, 2014, 54: 623-635. DOI:10.1016/j.conbuildmat.2013.12.097 |
| [19] |
Deng Huafeng,Zhu Min,Li Jianlin,et al. Study of mode-Ⅰ fracture toughness and its correlation with strength parameters of sandstone[J]. Rock and Soil Mechanics, 2012, 33(12): 3585-3591. [邓华锋,朱敏,李建林,等. 砂岩Ⅰ型断裂韧度及其与强度参数的相关性研究[J]. 岩土力学, 2012, 33(12): 3585-3591.] |
| [20] |
Zhang Z. An empirical relation between mode Ⅰ fracture toughness and the tensile strength of rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2002, 39(3): 401-406. DOI:10.1016/S1365-1609(02)00032-1 |
| [21] |
Barry N W,Raghu N S,Gexin S.Rock fracture mechanics:Principles,design and applications[M].Amsterdam:Elsevier Science Ltd,1992.
|
| [22] |
Wang J J,Zhu J G,Chiu C F,et al. Experimental study on fracture toughness and tensile strength of a clay[J]. Engineering Geology, 2007, 94(1/2): 65-75. |
| [23] |
Lakshmikantha M R,Prat P C,Ledesma A. Discussion on " Experimental study on fracture toughness and tensile strength of a clay” [Engineering Geology 94 (2007) 64–75][J]. Engineering Geology, 2008, 101(3/4): 295-296. |
| [24] |
Ren L,Zhu Z,Yang Q,et al. Investigation on the applicability of several fracture criteria to the mixed mode brittle fractures[J]. Advances in Mechanical Engineering, 2013, 5: 545108. DOI:10.1155/2013/545108 |
| [25] |
Khan S M A,Khraisheh M K. A new criterion for mixed mode fracture initiation based on the crack tip plastic core region[J]. International Journal of Plasticity, 2004, 20(1): 55-84. DOI:10.1016/S0749-6419(03)00011-1 |
| [26] |
Babadagli T,Develi K. Fractal characteristics of rocks fractured under tension[J]. Theoretical and Applied Fracture Mechanics, 2003, 39(1): 73-88. DOI:10.1016/S0167-8442(02)00139-8 |
| [27] |
Plouraboué F,Winkler K W,Petitjean L,et al. Experimental study of fracture surface roughness on rocks with crack velocity[J]. Physical Review E, 1996, 53(1): 277. DOI:10.1103/PhysRevE.53.277 |
| [28] |
Zhang Q B,Zhao J. Effect of loading rate on fracture toughness and failure micromechanisms in marble[J]. Engineering Fracture Mechanics, 2013, 102: 288-309. DOI:10.1016/j.engfracmech.2013.02.009 |
| [29] |
Rao Q,Sun Z,Stephansson O,et al. Shear fracture (Mode Ⅱ) of brittle rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2003, 40(3): 355-375. DOI:10.1016/S1365-1609(03)00003-0 |
| [30] |
Schmittbuhl J,Roux S,Berthaud Y. Development of roughness in crack propagation[J]. Europhysics Letters, 1994, 28(8): 585-590. DOI:10.1209/0295-5075/28/8/008 |
| [31] |
Backers T,Fardin N,Dresen G,et al. Effect of loading rate on Mode Ⅰ fracture toughness,roughness and micromechanics of sandstone[J]. International Journal of Rock Mechanics and Mining Sciences, 2003, 40(3): 425-433. DOI:10.1016/S1365-1609(03)00015-7 |
 2018, Vol. 50
2018, Vol. 50


