2. 武汉理工大学 土木工程与建筑学院,湖北 武汉 430070;
3. 哈尔滨工业大学 土木工程学院,黑龙江 哈尔滨 150090
2. School of Civil Eng. and Architecture, Wuhan Univ. of Technol., Wuhan 430070, China;
3. School of Civil Eng. Harbin Inst. of Technol., Harbin 150090, China
混合试验将结构的关键构件从整个结构中隔离出来作为试验子结构在试验室进行加载,其余部分则作为数值子结构进行数值建模分析。混合试验可满足大比例尺甚至足尺试件的要求,从而降低甚至消除尺寸效应的不利影响;且混合试验因试件数量较少而具有较高的经济性。因此,混合试验逐渐受到国内外学者的关注[1–2],成为研究结构抗震性能的重要方法之一。混合试验结果的准确性主要受逐步时间积分方法、作动器控制时滞以及数值子结构精度3方面因素影响[3–5]。作者主要从提高数值子结构的精度出发来提高混合试验的可靠性。模型更新是在现有单元、本构模型和积分算法等条件下,在数值模型确立后,通过对本构模型参数的识别与更新来提数值子结构的精度[6–8]。
土木工程领域,本构模型主要包括构件、截面和材料3个层次。构件本构模型描述的是结构构件(柱、梁等)的力–位移关系;截面本构模型描述的是截面弯矩、轴力–曲率的关系;材料本构模型表示的是材料应力–应变关系。目前,混合试验模型更新主要以构件本构模型为主,较少基于截面本构的模型更新[9]。从广义上讲,构件本构模型应考虑构件的截面形状、截面尺寸、配筋率、配箍率、轴压比、边界条件等因素。从狭义上讲,构件本构模型可以描述单一构件的力–位移关系的模型。混合试验模型更新中应用较广泛的Bouc-Wen模型和双折线模型都属于狭义上的构件本构模型。模型更新的前提条件是数值子结构中待更新的本构模型与试验子结构的数值本构模型相同。若对狭义的构件本构模型进行更新,则要求二者具有相同的轴压比、边界条件、配箍率等因素。从另一个角度讲,当结构构件类型较多时,对试验子结构的数量提出了较高要求,以满足不同数值子结构构件更新的需求。截面本构模型更新也具有类似的问题,它受到截面类型等因素的约束。因此,就通用性而言,材料本构模型参数更新最为适宜。
目前,混合试验模型更新中应用较多的非线性、在线参数识别方法主要有扩展卡尔曼滤波法(EKF)和隐性卡尔曼滤波法(UKF)。经过学者大量的研究与应用发现,与EKF方法相比,UKF方法能较好地实现对强非线性系统的在线参数识别,并且识别精度比EKF更高[6–8,10]。综上所述,梅竹等提出了一种基于UKF的材料本构模型参数的在线识别方法[11]。
将文献[11]中的在线参数识别方法应用于混合试验模型更新中,完成了钢筋混凝土框架的模型更新混合试验。试验结果表明,材料本构模型参数识别方法有较好的表现;通过更新该参数能有效提高混合试验数值子结构的精度,从而提高混合试验的可靠性。
1 混凝土本构模型参数识别尽管本研究关注的是混凝土本构模型参数的识别,但该方法同样可以应用于对其他材料本构模型参数的识别。
1.1 混凝土材料本构模型及参数敏感性在土木工程领域,本构模型是描述广义力与广义变形关系的函数,表达式如下:
| $F=f(D,{P})$ | (1) |
式中,
| $\left\{ \begin{array}{l} \sigma = \left( {1 + {K_{{\rm{s1}}}}{\rho _{\rm{s}}}} \right){f_{{\rm{cu}}}} \cdot \left[ {\frac{{2\varepsilon }}{{\left( {1 + {K_{{\rm{s2}}}}{\rho _{\rm{s}}}} \right){\varepsilon _{0{\rm{u}}}}}}} \right.\left. { - {{\left( {\frac{\varepsilon }{{\left( {1 + {K_{{\rm{s2}}}}{\rho _{\rm{s}}}} \right){\varepsilon _{0{\rm{u}}}}}}} \right)}^2}} \right],\\ \sigma = (1 + {K_{{\rm{s1}}}} \cdot {\rho _{\rm{s}}}){f_{{\rm{cu}}}} + \frac{{\left( {{K_{\rm{c}}} - 1} \right)(1 + {K_{{\rm{s1}}}} \cdot {\rho _{\rm{s}}}){f_{{\rm{cu}}}}}}{{(1 + {K_{{\rm{s3}}}} \cdot {\rho _{\rm{s}}}){\varepsilon _{{\rm{du}}}} - (1 + {K_{{\rm{s2}}}} \cdot {\rho _{\rm{s}}}){\varepsilon _{{\rm{0u}}}}}} \cdot \\ \;\;\;\;\;\;\;{\mkern 1mu} \left[ {\varepsilon - \left( {1 + {K_{{\rm{s2}}}} \cdot {\rho _{\rm{s}}}} \right)} \right]{\varepsilon _{{\rm{0u}}}} \end{array} \right.$ | (2) |
为便于理解,可将式(2)简洁表示为:
| $\sigma =g(\varepsilon ,{f_{{\rm{cu}}}},{\varepsilon _{{\rm{0u}}}},{\varepsilon _{{\rm{du}}}},{K_{\rm c}},{K_{{\rm{s1}}}},{K_{{\rm{s2}}}},{K_{\rm s3}},{\rho _{\rm{s}}})$ | (3) |
式中:
在所有参数中,最为敏感的3个本构参数
卡尔曼滤波估计(KF)通过两个主要步骤实现对状态量的估计。首先,通过状态方程式(4)获得状态量x在第
| ${\hat x}_k^ - ={f_k}({\hat x}_{k - 1}^ + )$ | (4) |
式中,“-”表示先验估计,“+”表示后验估计。然后,通过式(5)获得x在第
| ${\hat x}_k^ + ={\hat x}_k^ - + {{K}_k}({{y}_k} - {{\hat y}_k})$ | (5) |
式中:
| ${{\hat y}_k}={h_k}({\hat x}_k^ - )$ |
对于线性系统(
对于常参数识别问题,有
| ${{\hat x}_k}={{\hat x}_{k - 1}} + {{K}_k}({{y}_k} - {{\hat y}_k})$ | (7) |
| ${{\hat y}_k}={h_k}({{\hat x}_{k - 1}})$ | (8) |
式(6)或(8)是观测方程,描述的是观测量与待估参数之间的关系。其中,待估参数为混凝土本构模型参数。若观测量为应力,则式(2)也可作为观测方程,用于求出观测量的估计值。但当混凝土开裂后,尤其是当钢筋混凝土构件进入强非线性时,混凝土应力很难准确测量。同时,在混合试验中,试验构件的位移和恢复力是最为普遍的观测量,并且具有较高的精度。因此,以构件恢复力作为观测量。
若采用恢复力作为观测量会导致观测方程(也就是恢复力与本构参数之间的关系)很难解析表达。为此,作者提出采用OpenSees有限元软件计算观测量的估计值。简单地,就是通过OpenSees使用给定的本构参数样本点计算出恢复力样本点,进而获得观测量的估计值。为完成该功能,需要改写OpenSees源程序的部分代码,具体详见文献[11]。
2 混合试验架构 2.1 试验架构标准混合试验主要由3个模块组成,协调器、数值子结构和试验子结构。协调器控制整个拟动力试验,包括结构运动方程的逐步求解和数据的传输功能;数值子结构和试验子结构在收到协调器发送的相关自由度的位移后,进行加载并将获得的相应恢复力返回给协调器,然后,由协调器求解地震作用下结构在下一时间步上的位移。更新混合试验在标准混合试验的基础上添加了识别模块,如图1所示。
从图1中可以看出,增加了识别模块后,原来标准混合试验的并行程序变为串行程序,因为识别模块需要在试验子结构加载并测得恢复力后进行参数识别,数值子结构需要等待识别模块给出新参数进行更新后计算获得的恢复力。与标准混合试验相比,材料本构模型参数更新混合试验需要另外建立试验子结构的有限元模型,并且该模型采用与数值子结构相同的材料本构模型。选择适当的优化方法,用试验子结构的试验数据对试验子结构有限元模型中的材料本构模型参数进行优化,并将优化参数更新到数值子结构。
图1中,Re表示试验子结构测得的恢复力,Rn表示数值子结构计算的恢复力,P代表待识别更新的参数,Psamples代表参数的样本点,
 |
| 图1 混合试验模型更新流程图 Fig. 1 Flowchart of the proposed hybrid simulation with model updating |
值得注意的是,计算的恢复力样本点不仅仅由本构参数和输入位移确定,还与历史变量(前一步的应力应变状态)有关。这就要求,OpenSees基于相同的历史变量计算2
试验对象为单层单跨钢筋混凝土框架,如图2所示。取框架左柱为试验子结构,梁与右柱为数值子结构。为简化加载条件,以左柱一半的1/2缩尺模型为试验子结构,如图3所示。因假定梁为无穷刚,数值子结构可进一步简化为右柱的全尺寸模型。
 |
| 图2 钢筋混凝土平面框架 Fig. 2 Reinforced concrete plain fram |
根据长度单位相似关系
| ${l_{\rm{m}}}=S \cdot {l_{\rm{p}}}$ | (9) |
可得力单位的相似关系如下:
| ${F_{\rm{m}}}={S^2} \cdot {F_{\rm{p}}}$ | (10) |
式(9)~(10)中,
| 表1 协调器与子结构数据交换 Tab. 1 Data exchange between coordinator and substructures |
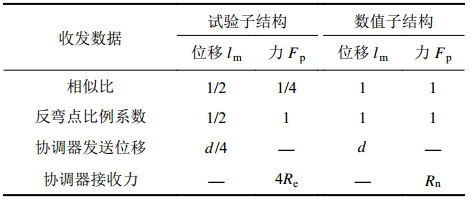 |
3 模型更新混合试验 3.1 参数初值
如第1.1节所述,约束与非约束混凝土的统一本构模型共有
通过材性试验,可获得混凝土的立方体抗压强度平均值
| ${\mu _{{\rm{fc}}}} =0.88\alpha {\text{×}} \mu _{{\rm{f150}}}^{\rm{s}} =42.7\;{\rm{MPa}}$ | (11) |
式中,
试件箍筋为直径4 mm的高强钢丝,对其进行3次拉伸试验,加载速度为1 000 N/min。试验结果表明钢丝无明显屈服平台。图4给出了其中一根钢丝的拉伸试验结果。
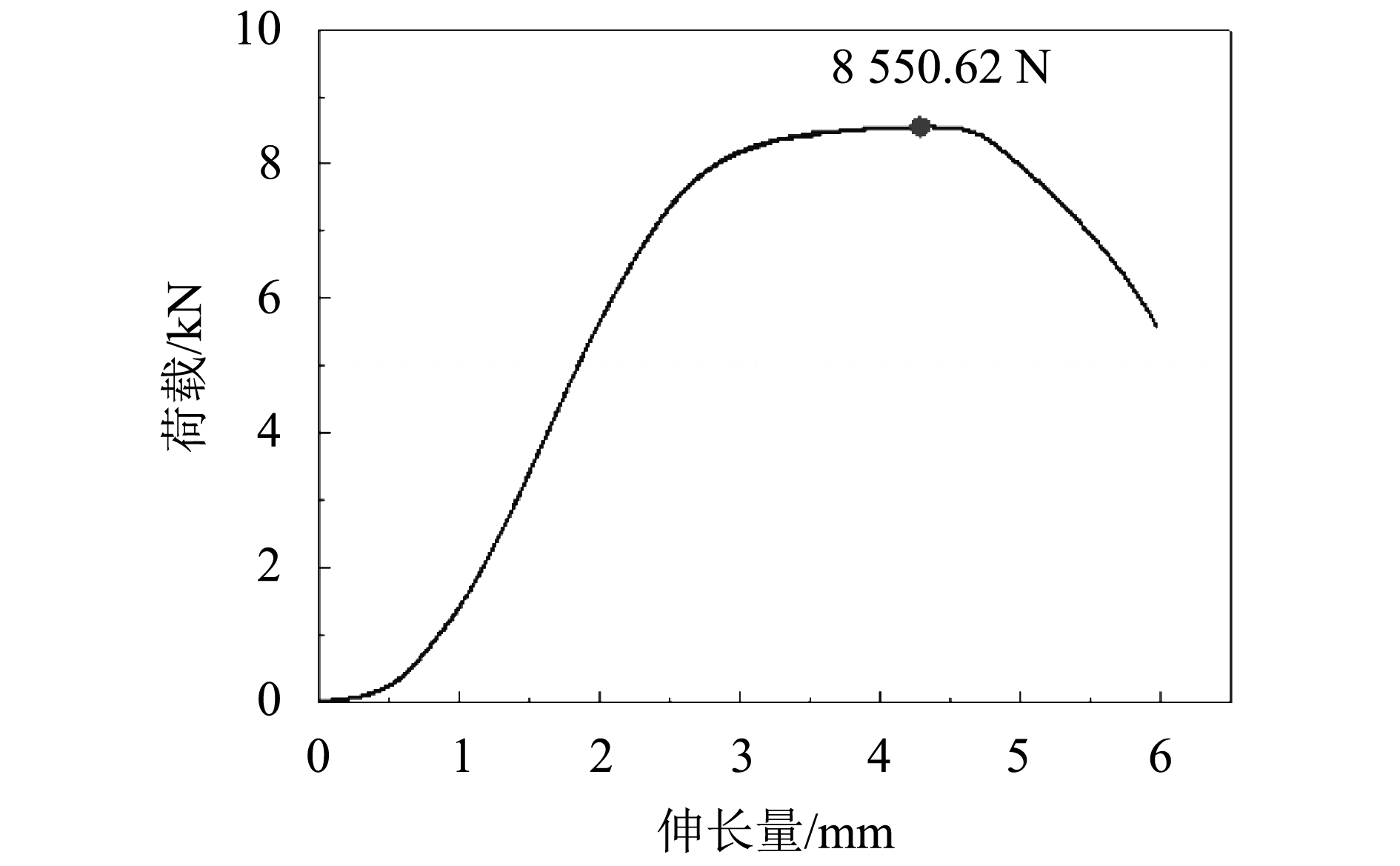 |
| 图4 箍筋拉伸试验结果 Fig. 4 Material experiment of the stirrup |
3次拉伸最大荷载分别为8 550.62、8 611.25和8 558.10 N,取平均值的85%为屈服荷载,获得箍筋屈服应力为fyh=579.9 MPa。最后获得混凝土本构参数的初值见表2所示。
| 表2 混凝土本构参数初值 Tab. 2 Initial values for concrete constitutive parameters |
 |
试件纵筋为直径10 mm的HRB335级钢筋。进行3次拉伸试验,加载速度为4 800 N/min。获得钢筋下屈服力为354 MPa,弹性模量
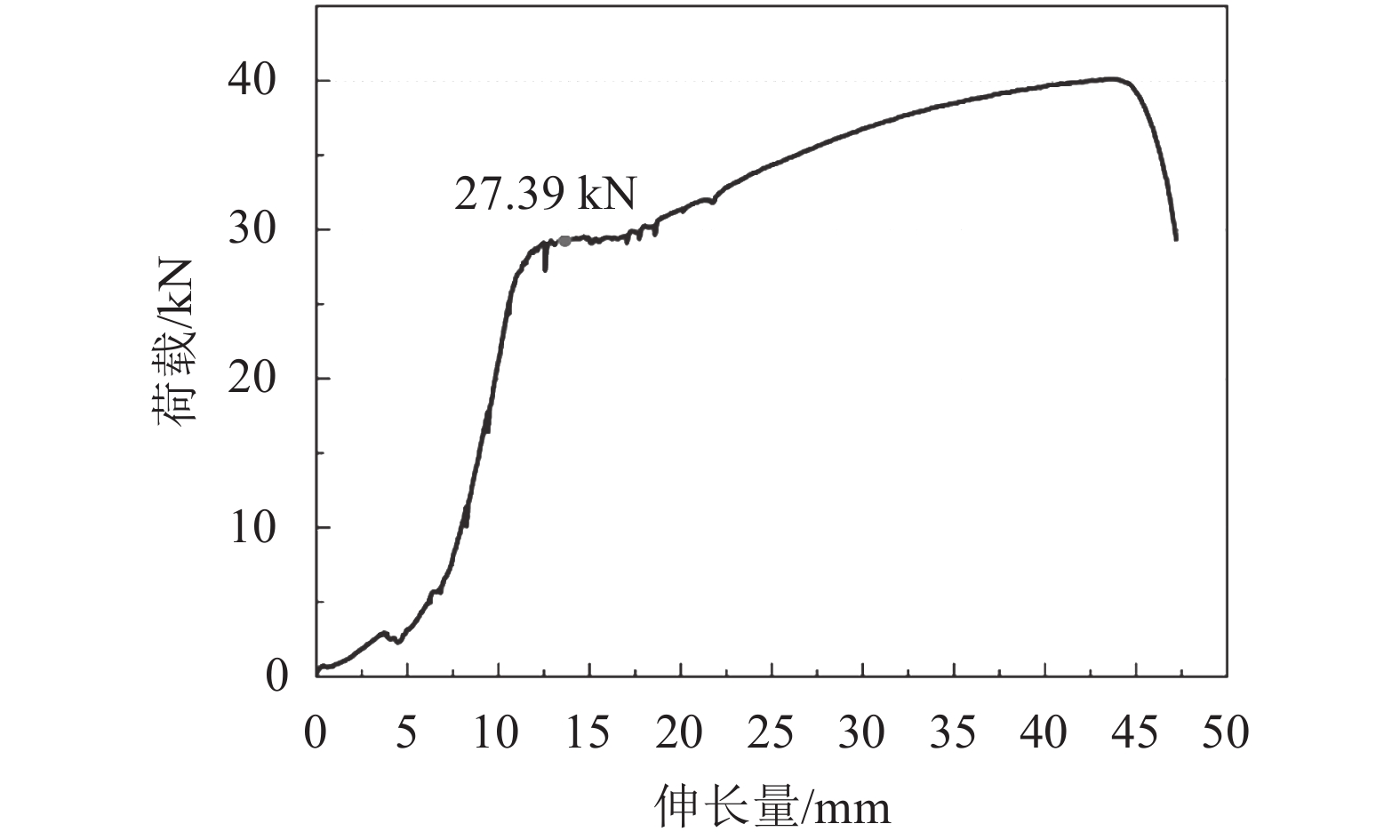 |
| 图5 纵筋拉伸试验结果 Fig. 5 Material experiment of the reinforced bars |
3.2 试验工况
本次混合试验共分为3个工况:标准工况、更新工况与参考工况,详见表3。标准工况的试验子结构(图3)在哈尔滨工业大学抗震试验室完成物理加载;数值子结构中混凝土本构模型参数采用表2所示的初值,纵向钢筋本构模型参数采用第3.1节材性试验获得的参数值;在试验过程中,钢筋与混凝土本构模型参数值保持不变。
| 表3 平面框架混合试验工况 Tab. 3 Cases of hybrid simulation on plain frames |
 |
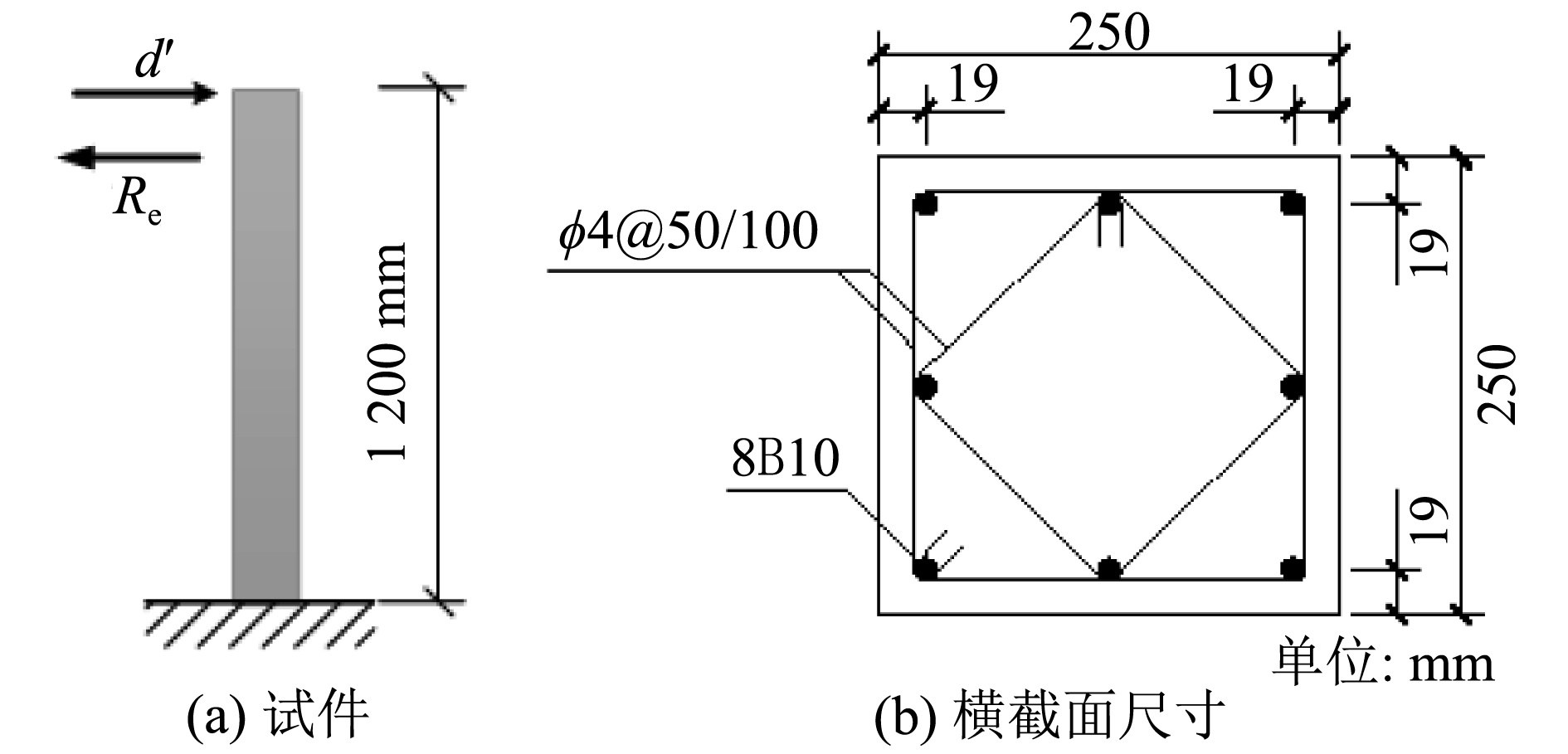 |
| 图3 试件尺寸图 Fig. 3 Dimension of the column and its cross section |
更新工况与标准工况的试验子结构是相同的,区别在于数值子结构的混凝土本构模型参数是否有更新;更新工况中,混凝土本构模型参数值在试验的每一步都采用参数识别获得的当前步最优参数值进行更新。
参考工况中,试验子结构是通过有限元模型模拟的,它与数值子结构中材料本构模型参数采用的都是更新工况中参数识别的最终收敛值。
3.3 试验结果选择调幅加速度峰值0.4g的El-Centro(NS, 1940)作为地震输入。工况2中参数识别结果如图6所示。3种工况的力–位移曲线和位移时程对比结果如图7所示。
因为在PGA=0.4g的地震荷载作用下,混凝土没有进入到本构模型下降阶段。所以,只与本构模型下降段函数相关的参数
从图6中可以看出,混凝本构模型参数识别表现较好,参数能够稳定、快速地收敛。通过数值模拟分析可知,本文的参数识别方法能够使参数较快、较稳定地收敛于真实值[11]。同时,从图6(c)可以看出,采用识别获得最优参数的有限元模型所提供的构件恢复力的计算值与试验构件的实测恢复力吻合较好,一致性较高。因此,可以认为所提出的参数识别方法能够在试验过程中提供稳定、可靠的参数识别结果。
 |
| 图6 更新混合试验参数识别结果 Fig. 6 Results of parameter identification |
由图7中混合试验3种工况结果对比可以看出,本文提出的基于混凝土本构模型参数更新的混合试验比无更新的标准混合试验有较明显的提高。
 |
| 图7 混合试验3种工况对比 Fig. 7 Comparison of the three cases of hybrid simulation |
4 结 论
提出了基于混凝土本构模型参数在线识别与更新的混合试验方法。结合混凝土与钢筋的材性试验,给出了混凝土本构参数初值的确定方法。分别在两个钢筋混凝土平面框架上完成了数值子结构无更新的标准混合试验和有更新的更新混合试验。同时,采用参数识别的收敛值模拟了该框架的混合试验。3种工况混合试验的对比结果表明:
1) 混凝土本构参数识别方法对于强非线性系统识别问题具有较好的稳定性,在试验过程中参数具有较好的收敛速度,且对试验观测噪声具有较好的鲁棒性,可以在其他类型结构的更新混合试验中进一步推广。
2) 开发了OpenSees模型更新模块,解决了UKF方法中非线性观测方程难以解析表达的问题,扩大了UKF方法在混合试验中的应用范围。
3) 通过给标准混合试验增加模型更新模块,实现了混凝土本构模型参数的识别与更新,提高了混合试验数值子结构的准确性,从而提高了混合试验结果的可靠性。
| [1] |
Zhang Yu,Pan Peng. Parallel computing method for structural seismic response analysis considering interaction between substructures[J]. Engineering Mechanics, 2013, 30(5): 118-124. [张钰,潘鹏. 考虑子结构间相互作用的结构地震反应并行计算方法研究[J]. 工程力学, 2013, 30(5): 118-124. DOI:10.6052/j.issn.1000-4750.2012.01.0056] |
| [2] |
Pinto A V,Pegon P,Magonette G,et al. Pseudo-dynamic testing of bridges using non-linear substructuring[J]. Earthquake Engineering and Structural Dynamics, 2004, 33: 1125-1146. DOI:10.1002/eqe.393 |
| [3] |
Lamarche C P,Bonelli A,Bursi O S A. Rosenbrock-W method for real-time dynamic substructuring and pseudo-dynamic testing[J]. Earthquake Engineering and Structural Dynamics, 2009, 38(9): 1071-1092. DOI:10.1002/eqe.884 |
| [4] |
Wang Zhen,Liu Jinjin,Wu Bin. Parameter determination of nearly-complete compensation scheme for time delay in real-time hybrid simulation[J]. Engineering Mechanics, 2014, 31(10): 158-166. [王贞,刘进进,吴斌. 实时混合试验近完全时滞补偿方法的参数确定[J]. 工程力学, 2014, 31(10): 158-166. DOI:10.6052/j.issn.1000-4750.2013.05.0386] |
| [5] |
Abbiati G,Bursi O S,Caparan P. Hybrid simulation of a multi-span RC viaduct with plain bars and sliding bearings[J]. Earthquake Engineering and Structural Dynamics, 2015, 44(13): 2221-2224. DOI:10.1002/eqe.2580 |
| [6] |
Wang Tao,Wu Bin. Hybrid testing method based on model updating with constrained unscented Kalman filter[J]. Journal of Earthquake Engineering and Engineering vibration, 2013, 33(5): 100-109. [王涛,吴斌. 基于约束UKF模型更新的混合实验方法[J]. 地震工程与工程振动, 2013, 33(5): 100-109. DOI:10.13197/j.eeev.2013.05.100.wangt.013] |
| [7] |
Kwon O S. Model updating method for substructure pseudo-dynamic hybrid simulation[J]. Earthquake Engineering & Structural Dynamics, 2013, 42(13): 1917-1984. DOI:10.1002/eqe.2307 |
| [8] |
Hashemi M J,Masroor A. Implementation of online model updating in hybrid simulation[J]. Earthquake Engineering and Structural Dynamics, 2014, 43(3): 395-42. |
| [9] |
Wu Bin,Chen Yongsheng,Xu Guoshan,et al. Hybrid simulation of steel frame structures with sectional model updating[J]. Earthquake Engineering and Structural Dynamics, 2016, 45: 1251-1269. DOI:10.1002/eqe.2350 |
| [10] |
Song W,Dyke S. Real-time dynamic model updating of a hysteretic structural system[J]. Journal of Structural Engineering, 2014, 140(3): 1-14. DOI:10.1061/(ASCE)ST.1943-541X.0000857 |
| [11] |
Mei Zhu,Wu Bin,Yang Ge. Online parameter identification of concrete constitutive model[J]. Engineering Mechanics, 2016, 33(7): 108-115. [梅竹,吴斌,杨格. 钢筋混凝土结构材料本构模型参数的在线识别[J]. 工程力学, 2016, 33(7): 108-115. DOI:10.6052/j.issn.1000-4750.2014.12.1033] |
| [12] |
Julier S.A general method for approximating nonlinear transformations of probability distributions[D].Oxford:University of Oxford,1996:1–27.
|
 2018, Vol. 50
2018, Vol. 50


