2. 中国公路工程咨询集团有限公司,北京 100089;
3. 中国铁道科学研究院 基础设施检测研究所,北京 100081
2. China Highway of Eng. Consultants Corp., Beijing 100089, China;
3. Infrastructure Inspection Research Inst., China Academy of Railway Sciences, Beijing 100081, China
拉索结构作为桥梁结构中重要构成部分,与其他主要受力构件如塔、拱或梁共同承担外部荷载作用。索力测试方法、影响因素、计算方法和检定标准是这类拉索结构研究的关键。
索力测试常用方法主要分为接触式和非接触式两种。对于接触式测量方法,如振动频率法[1]、磁通量法[2]和三点弯曲法[3]等。对于振动频率法,运用快速Fourier变换法[4]可对拉索固有频率进行精确搜索,基于此原理,赵雪峰等[5]开发了无线索力测量系统。此外,光纤光栅传感器测定索力法是一种新型接触式测试方法,朱万旭等[6]提出了通过锚固在拉索锚杯外壁的光纤光栅传感器测量应变值换算索力的方法;Zheng Rui等[7]利用胶粘于拉索钢丝上的内置式光纤光栅传感器监测索力。对于非接触式索力测量方法,Feng等[8]提出一种基于视觉传感器精确测定拉索拉力的方法;Yan Banfu等[9]提出一种基于视觉的目标跟踪和基于频域分解的任意边界条件下的索力估算方法。
影响索力测量精度的主要因素有抗弯刚度、边界约束条件、斜度、垂度,索的初应力、拉索类型[2]和外部环境影响因素等。当拉索边界条件明确时可采用传统索力实用计算式或对双曲线函数项进行近似处理的近似频率计算式[10],当拉索边界条件不确定时,宜采用Euler梁法或Timoshenko梁法进行索力识别[11]。对于斜拉索的垂度效应,现有规范[12–13]考虑采用Ernst公式进行修正拉索弹性模量,主要是由于拉索倾角变小时,垂度效应对拉索自振频率的影响增大[14]。外部环境对拉索力学特性的影响较大。对于温度效应影响方面,任远等[15]通过试验结果发现温度与索力线性相关性,但不同索长的温度效应对索力影响程度不同。此外,钢索在高温条件下的力学性能取决于拉索截面的组成如平行钢丝或钢绞线[16];对于风雨振影响方面,斜拉索多模态风雨激振主要发生在第一阶模态,且平面内拉索振动大于平面外振动[17]。故对于长周期大跨度斜拉桥,斜拉索振动效应对结构振动的影响不能忽视[18],还应考虑索–桥–塔耦合的拉索振动影响[19]。对于悬索桥,还应考虑锚固系统对桥梁锚跨索股的索力–频率的影响[20]。异形拱桥的索力需考虑非线性的影响[21]。
索力计算一般基于弦振动理论和能量法由索长、索单位重量和实测频率求解,若拉索张力产生的几何刚度大于物理刚度[22]时,可忽略拉索抗弯刚度进行简化计算。若为避免振动频率法中引入拉索抗弯刚度的计算误差,可按照查利权[23]推导出的两端简支拉索实测频率值、频率阶数之间的数学关系式计算索力。频差法、两点法[24]也是由同一荷载状态下拉索的高、低频求解索力的两种方法。
现有检定标准中评价索力指标有索力偏差率[25–26]、索力校验系数和频率校验系数[27],其未超限检定标准为实测索力与设计值偏差率位于±10%以内[25]。索力校验系数和频率校验系数计算均基于拉索频率。
拉索结构在铁路桥梁中运用越来越广泛,而2004版《铁路桥梁检定规范》[4]中暂无相应条文,更无相应的拉索索力检定要求,且现有桥梁规范或理论研究仅限于索力或频率的检定要求,更无拉索索力增量校验系数的可行性研究。在计算校验系数时,对于索力实测值,拉索索长应如何合理选取,对于索力理论计算值,有限元模型如何确定,鲜有文献或规范对其进行相应的研究。基于此,作者建议了一种索力简化计算方法和索力增量校验系数检定方法。通过理论推导和试验案例分析,建立有限元模型验证索力精确求解方法的正确性。通过与精确求解方法比较,验证本文索力简化计算方法合理性。采用振动频率校验系数、索力校验系数和索力增量校验系数等3种系数对索力进行技术状况评定分析,验证索力增量校验系数方法的合理性。
1 理论方法推导 1.1 索力求解方法 1.1.1 索力精确求解方法计算假定:1)拉索垂跨比很小,其值不大于0.02时为小垂度,曲线形态接近直线[24],且不出现复形索情形;2)拉索只沿着法线方向振动[28];3)采用经典梁理论,不考虑温度的影响,不考虑截面内的剪切作用,外荷载作用下拉索伸长量较拉索索长非常小;4)拉索中间无自重以外的附加荷载。
拉索求解计算示意图见图1。
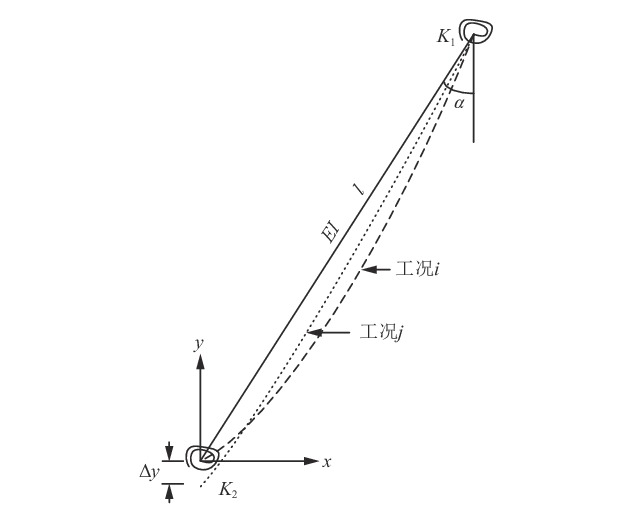 |
| 图1 拉索计算示意图 Fig. 1 Cable computation diagram |
设图1中的拉索荷载工况
| ${y_k} = {\varphi _k}(x)\sin \;({\omega _k}t + \theta )/\sin\; \alpha $ | (1) |
式中,
利用弦振动理论,建立任意荷载工况
| $EI\frac{{{\partial ^4}{y_k}}}{{\partial {x^4}}} - {T_k}\frac{{{\partial ^2}{y_k}}}{{\partial {x^2}}} + \rho \frac{{{\partial ^2}{y_k}}}{{\partial {t^2}}} = 0$ | (2) |
式中,
结合式(1)和(2),对于任意的
| $EI\frac{{{\partial ^4}{\varphi _k}(x)}}{{\partial {x^4}}} - {T_k}\frac{{{\partial ^2}{\varphi _k}(x)}}{{\partial {x^2}}} - \rho \omega _k^2{\varphi _k}(x) = 0$ | (3) |
其通解为:
| $ \begin{aligned}[b] {\varphi _k}(x) = & {A_k}\sin\; {a_n}x + {B_k}\cos\; {a_n}x\;+\\ & {C_k}\sinh\; {a_n}x + {D_k}\cosh\; {a_n}x \end{aligned}$ | (4) |
式中:系数
任意荷载工况
| ${E_k} = \frac{1}{2}\int_0^l {\rho {{\left(\frac{{\partial {y_k}}}{{\partial t}}\right)}^2}{\rm{d}}x} $ | (5) |
则
任意荷载工况
| ${V_k} = \frac{1}{2}\int_0^l {EI{{\left(\frac{{{\partial ^2}{y_k}}}{{\partial {x^2}}}\right)}^2}{\rm{d}}x} + \frac{1}{2}\int_0^l {{T_k}{{\left(\frac{{\partial {y_k}}}{{\partial x}}\right)}^2}{\rm{d}}x} $ | (6) |
则
| ${V_{k, \max }} = \frac{1}{2}\int_0^l {\left(EI{{\left(\frac{{{\partial ^2}{\varphi _k}(x)}}{{\partial {x^2}}}\right)}^2} + {T_k}{{\left(\frac{{\partial {\varphi _k}(x)}}{{\partial x}}\right)}^2}\right){\rm{d}}x} {\text{。}}$ |
由能量守恒定律
| $\omega _k^2 = \frac{{EI\displaystyle\int_0^l {{{\left(\dfrac{{{\partial ^2}{\varphi _k}(x)}}{{\partial {x^2}}}\right)}^2}{\rm{d}}x} + {T_k}\int_0^l {{{\left(\dfrac{{\partial {\varphi _k}(x)}}{{\partial x}}\right)}^2}{\rm{d}}x} }}{{\rho \displaystyle\int_0^l {\varphi _k^2(x){\rm{d}}x} }}$ | (7) |
索自重作用下的自振频率求解可将式(7)中
拉索索力
| ${T_k} = \dfrac{{\rho \omega _k^2\displaystyle\int_0^l {\varphi _k^2(x){\rm{d}}x} - EI\int_0^l {{{\left(\dfrac{{{\partial ^2}{\varphi _k}(x)}}{{\partial {x^2}}}\right)}^2}{\rm{d}}x} }}{{\displaystyle\int_0^l {{{\left(\dfrac{{\partial {\varphi _k}(x)}}{{\partial x}}\right)}^2}{\rm{d}}x} }}$ | (8) |
代入两端固定、两端铰支和固定+铰支等3种边界条件表达式,得到无外载作用时的第
| 表1 拉索索力计算参数 Tab. 1 Calculation parameters of cable force |
 |
自振圆频率
| ${\omega _{k, n}} = {\chi _{k, n}}{\left(\frac{{\text{π}} }{l}\right)^2}\sqrt {\frac{{EI}}{\rho }} $ | (9) |
振型系数
当
对于抗弯刚度和边界条件对拉索振动频率的影响在实际工程检测中的考虑,李国强等[22]考虑按描述垂度影响的无量纲Irvine系数
| $ \left\{ {\begin{aligned} & {{\lambda _{\!\!\!\text{ Ⅰ}}^2}= {{(\rho gl/{T_k})}^2}(EAl/T{l_{\rm e}})}, \\ & {\mu = l\sqrt {{T_k}/EI} }, \\ & {\psi = {\kappa _{\rm s}}l/{T_k}}, \end{aligned}} \right. k = j, i $ | (10) |
式中:
| ${l_e} = l\left[1 + \frac{8}{3}{\left(\frac{\delta }{l}\right)^2} - \frac{{32}}{5}{\left(\frac{\delta }{l}\right)^4} + \cdots\right]$ | (11) |
当
由拉索自由振动的静力分析,当
由不考虑支座振动索力动力检测理论分析,当
当索两端支承刚度
对于倾斜拉索,一般通过拉索垂度效应考虑斜拉索倾角对索力大小的影响。日本土木学会[30]给出了应力变化范围和荷载变化范围内Ernst斜拉索刚度修正公式(式(12))。
对于倾斜角为
| $E = \frac{{{E_0}}}{{1 + \dfrac{{{{(\rho {l_{\rm a}}\cos\; \alpha )}^2}({\sigma _i} + {\sigma _j})}}{{24\sigma _i^2\sigma _j^2}}{E_0}}}$ | (12) |
式中,
若拉索平面外刚度
| $ \Delta {T_k} = \frac{{2\rho {\omega _k}\displaystyle\int_0^l {\varphi _k^2(x){\rm d}x} }}{{\displaystyle\int_0^l {{{\left(\dfrac{{\partial {\varphi _k}(x)}}{{\partial x}}\right)}^2}{\rm d}x} }}\Delta {\omega _k},\;k = j, i $ | (13) |
即
| ${T\!_j} = (2{\omega _j}/{\omega _i} - 1){T_i}$ | (14) |
相应地,外载作用前后的索力偏差率
| ${K_t} = 2({\omega _j}/{\omega _i} - 1)$ | (15) |
与精确求解法相比,该简化计算式只需仅恒载作用下的振动频率、索力及外载作用前后的振动频率便可求解得到外载作用下的索力,故更为简单。
1.1.3 按索端位移确定的索力理论方法对于悬链型拉索,索端位移变化量按照弧长变化量确定。设工况
| ${H_k} = {T_k}\cos \;\theta $ | (16) |
悬链型拉索无应力原长公式[24]:
| ${S_{0, k}} = \frac{{{H_k}}}{\rho }(\tan \;\theta - \tan \;{\theta _{\rm d}})$ | (17) |
令拉索低端
| ${S_{0, k}} = \frac{{{H_k}}}{\rho }(\sinh\; u - m)$ | (18) |
悬链型拉索的任意弧长公式[24]:
| $ \begin{aligned}[b] {S\!_k} = & \frac{{{H_k}}}{\rho }[\sinh\; u - m + \frac{{{H_k}}}{{2E{A_0}}}(\sinh \;u\cosh\; u\;+\\ & u - m\sqrt {1 + {m^2}} - {\rm{arsinh}}\;m)] \end{aligned}$ | (19) |
将式(19)与(17)相减,再在其减式两端取水平索力H 的微分方程,得到外部荷载作用前后相对于无应力索长的索端位移变化量为:
| $\frac{{\Delta {S_k}}}{{{S\!_k} - {S\!_0}}} = \frac{{2\Delta {H_k}}}{{{H_k}}}$ | (20) |
整理得
假定外部荷载作用前后与水平方向的转角变化不大,即
| $\Delta {l_{ji}} = \left(\frac{{{T_j}}}{{{T_i}}} - 1\right)\frac{{T_i^2}}{{\rho E{A_0}}}{\chi _i}\sin \;{\theta _i}\cos\; {\theta _i}$ | (21) |
| $\begin{aligned}{\text{其中,}}{\chi _i}= & \tan\;{\theta _i}{\sqrt {1 + {{\tan }^2}\theta } _i} - \tan\;{\theta _{\rm d}}\sqrt {1 + {{\tan }^2}{\theta _{\rm d}}}+ \\ & \ln\dfrac{{\tan\;{\theta _i} + \sqrt {1 + {{\tan }^2}{\theta _i}} }}{{\tan\;{\theta _{\rm d}}+\sqrt {1 + {{\tan }^2}{\theta _{\rm d}}} }}{\text{。}}\end{aligned}$ |
对于竖直拉索,拉索伸长量仅在拉索轴向变化,故不采用悬链线求解方法。假定无外载作用时的拉索初始索长为
| ${l_k} = {l_{\rm{0}}} + \frac{{{T_k}{l_k}}}{{E{A_i}}} + \frac{{{q_0}l_0^2}}{{{\rm{2}}E{A_i}}}$ | (22) |
则其相对伸长量
| $\Delta {l_{ji}} = \frac{{{T_j}{l_j} - {T_i}{l_i}}}{{E{A_i}}}$ | (23) |
相应地,相对于初始条件
| ${T_k} = E{A_k}({l_k} - {l_0})/{l_k}$ | (24) |
桥梁结构振动频率校验系数
| ${\eta _\omega } = {\omega _{\rm t}}/{\omega _{\rm c}}$ | (25) |
式中,
公路桥梁JTG/TJ21–2011[26]、城市桥梁CJJ/T 233–2015[2]中引入索力偏差率
| ${K_{\rm t}} = ({T_{\rm t}} - {T_{\rm c}})/{T_{\rm c}}$ | (26) |
式中,
| ${\eta _{\rm t}} = {T_{\rm t}}/{T_{\rm c}}$ | (27) |
显然,索力偏差率与1的和即为索力校验系数,即
索力增量校验系数可定义为拉索索力增量实测值与理论值的比值,见式(28)。
| ${\eta _{\Delta t}} = \Delta {T_{\rm t}}/\Delta {T_{\rm c}}$ | (28) |
式中,
拉索在伸长的过程中面积变化忽略不计,按照材料力学知识,通过竖直拉索索端位移差
| $\Delta {T_{\rm c}} = E{A_i}\Delta {l_{ji}}{\rm{/}}{l_i}$ | (29) |
实测索力增量值
| $\Delta {T_{\rm t}} = {\rm{2}}({\omega _j}/{\omega _i} - 1){T_i}$ | (30) |
式中,下标
外部荷载作用前后的索力增量校验系数
| ${\eta _{\Delta t}} = {\rm{2}}\left(\frac{{{\omega _j}}}{{{\omega _i}}} - 1\right)\frac{{{l_i}{T_i}}}{{E{A_i}\Delta {l_{ji}}}}$ | (31) |
这里
索力增量校验系数
依据索力偏差率不大于10%[2,26]的要求,并结合《公路斜拉桥设计细则》中关于运营阶段索力安全系数不小于2.5的规定及考虑抗弯刚度的影响参数
以主跨为48 m的某系杆拱桥[32](图2)中主跨第2孔为例,对以上理论推导进行验证,其结构形式为钢管混凝土拱连续梁结构形式,拱肋横桥向中心矩为9.72 m。
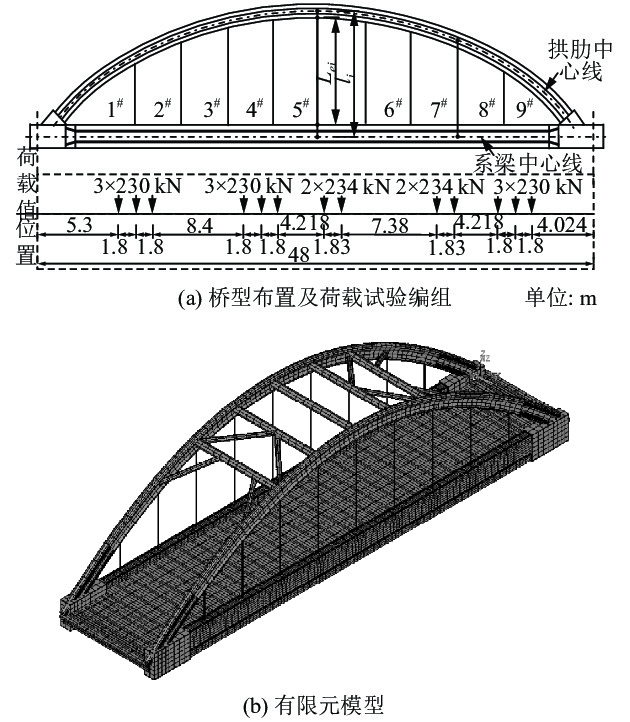 |
| 图2 实例桥概况 Fig. 2 Introduction of case bridge |
吊杆间距为4.4 m,全桥共18根吊杆,吊杆边界条件为两端铰支。每根吊杆由
| 表2 吊索长度及实测基频 Tab. 2 Cable lengths and tested basic frequencies |
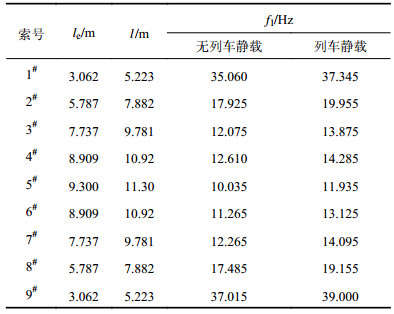 |
采用频率法测试吊杆索力,是在吊杆上布设振动传感器,运用锤击或利用大地脉动获得振动时域波形,经频谱分析得到吊索的多阶振动频率,无列车静载和列车静载作用下测得的各吊杆振动频率结果如表2所示。
吊杆索力振动测试的列车试验编组由DF4单机+C70满载重车1辆列车+DF4单机组合而成,列车组总长为50.676 m。结构最不利荷载工况的荷载值及位置见图2(a),其中双线加载作用的起始位置位于列车头第1轴轮距图2(a)中左侧梁端5.3 m,此时系梁轴拉力、拱肋轴压力和系梁跨中挠度均最大。
案例分析中分别建立全桥有限元模型和仅拉索的有限元模型,其中全桥模型分析全桥协同作用下的静动力特性,仅拉索的有限元模型主要分析拉索自身的振动特性,两者均采用ANSYS 14.5软件建立有限元模型,见图2(b)。系梁、拱肋和横梁均采用BEAM188单元,吊杆采用LINK10单元,二期恒载考虑道砟和钢轨重量。列车静载按照图2(a)中双线加载工况施加于有限元模型上相应位置处。外部静载作用下的系梁跨中轴拉力为1 838.1 kN,弯矩为2 414.4 kN,跨中竖向挠度为11.545 mm,分别与报告[32]中的实测数据相近,固有频率计算1阶模态为全桥横弯,与文献[33]中计算模态相同,故有限元模型计算可靠。
2.2 索力精确求解方法验证为验证第2.1节中的索力精确求解公式,以实例桥中有效长度
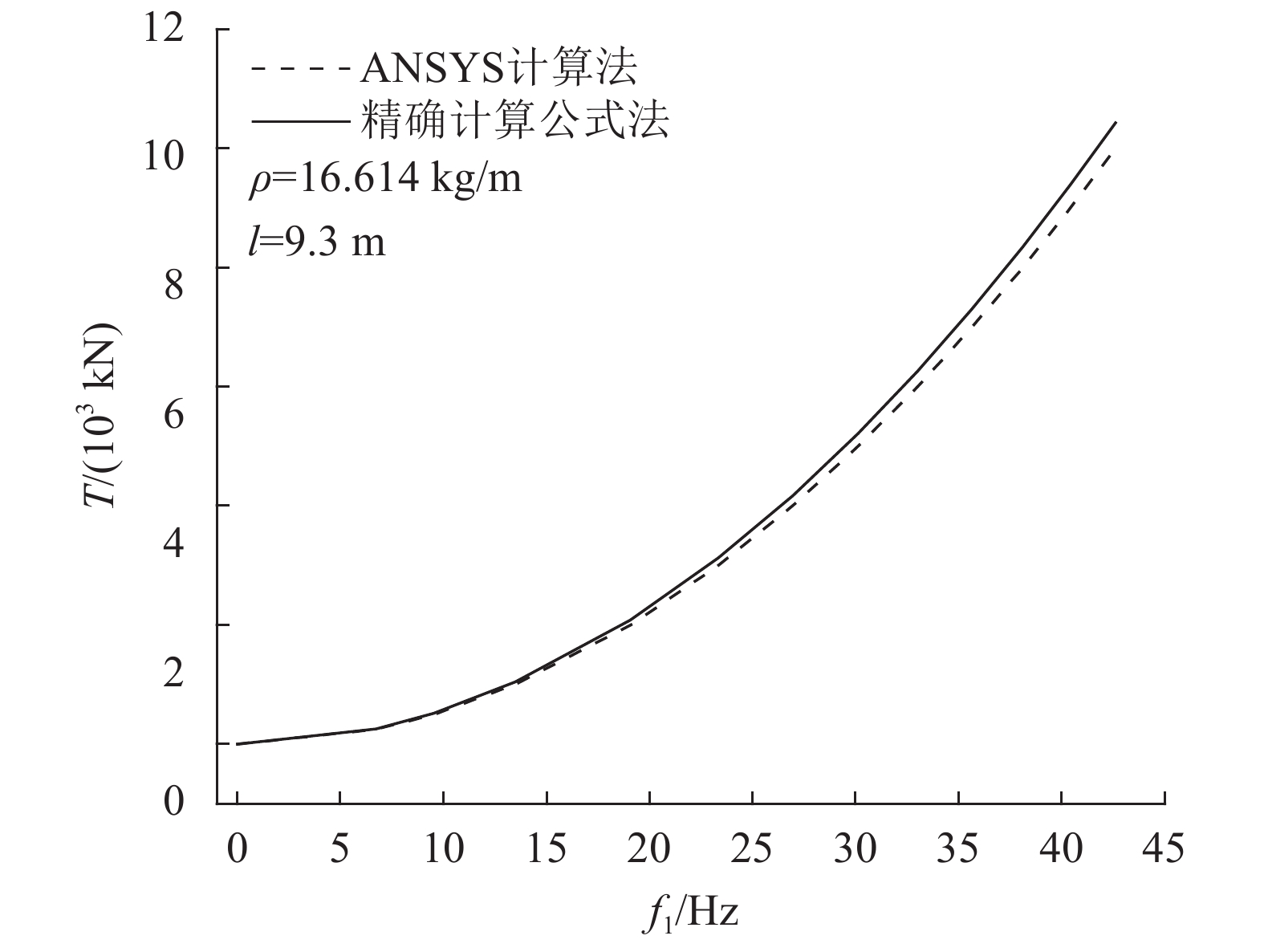 |
| 图3 拉索索力计算公式验证 Fig. 3 Calculation equation verification of cable forces |
由图3中索力–振动频率之间的关系可知,精确求解方法的计算结果与有限元计算结果吻合较好,特别是作用的外部荷载较小时吻合程度更高。
2.3 索力简化计算法比较对其外载作用前后的实测频率及其对应的索力采用按表1中精确求解公式法和本文中简化计算法进行比较。图4显示了两种方法的比较情况,本文简化方法索力略小于表1中精确计算公式;较精确求解公式法,简化公式法的最大误差分别不超过2.539%,故简化计算公式法计算可行。
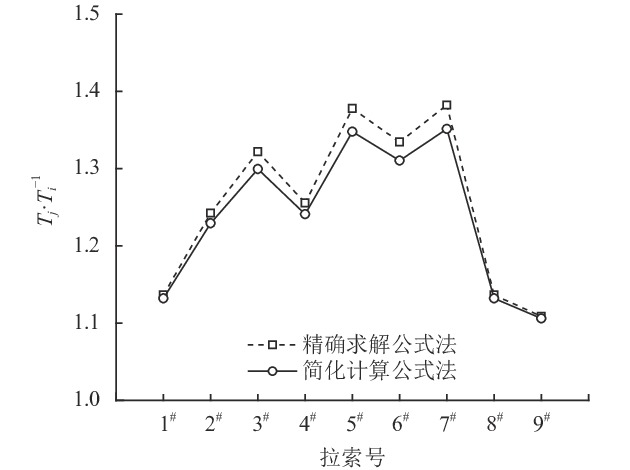 |
| 图4 两种计算方法索力比较 Fig. 4 Comparison of cable forces between two calculation methods |
2.4 索力和频率比较
为研究拉索振动特性,比较并分析了荷载作用前后的索力、索力差及频率3个参数的影响情况。其中:拉索索力、索力差分别由列车荷载作用前后的全桥有限元模型计算;频率由仅拉索有限元模型计算,其中频率计算中考虑与全桥有限元模型相同的索端变位和索力等效两种计算方式。
图5显示了有限元计算和按精确求解方法确定的实测索力比较情况。由图5的计算结果可知,全桥有限元模型中按照有效索长和实测频率确定的计算索力
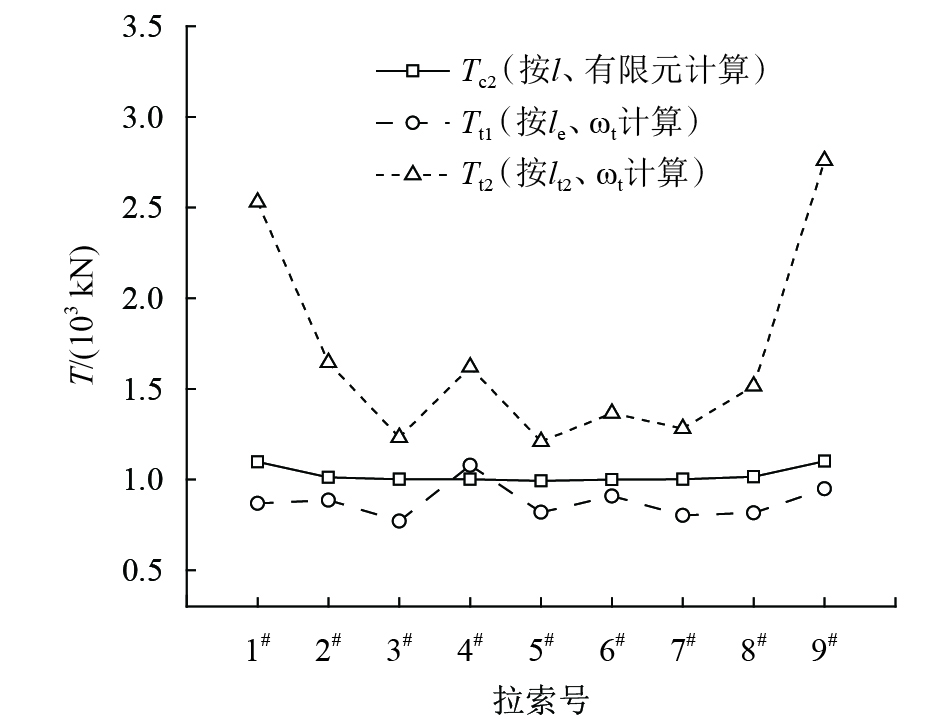 |
| 图5 索力比较 Fig. 5 Comparison of cable forces |
图6显示了通过索端位移差和实测频率确定的拉索的索力差比较情况。由图6中的计算结果可知,仅拉索有限元分析模型中按照有效索长和实测频率确定的计算索力差
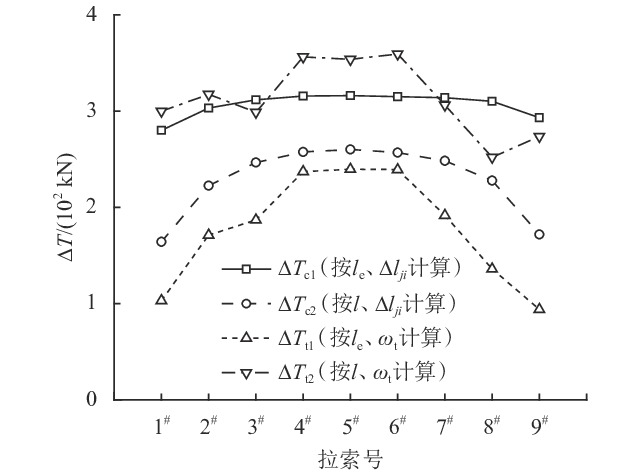 |
| 图6 索力差比较 Fig. 6 Comparison of cable force variations |
图7显示了仅拉索有限元模型计算和实测频率比较情况。图7中实测频率
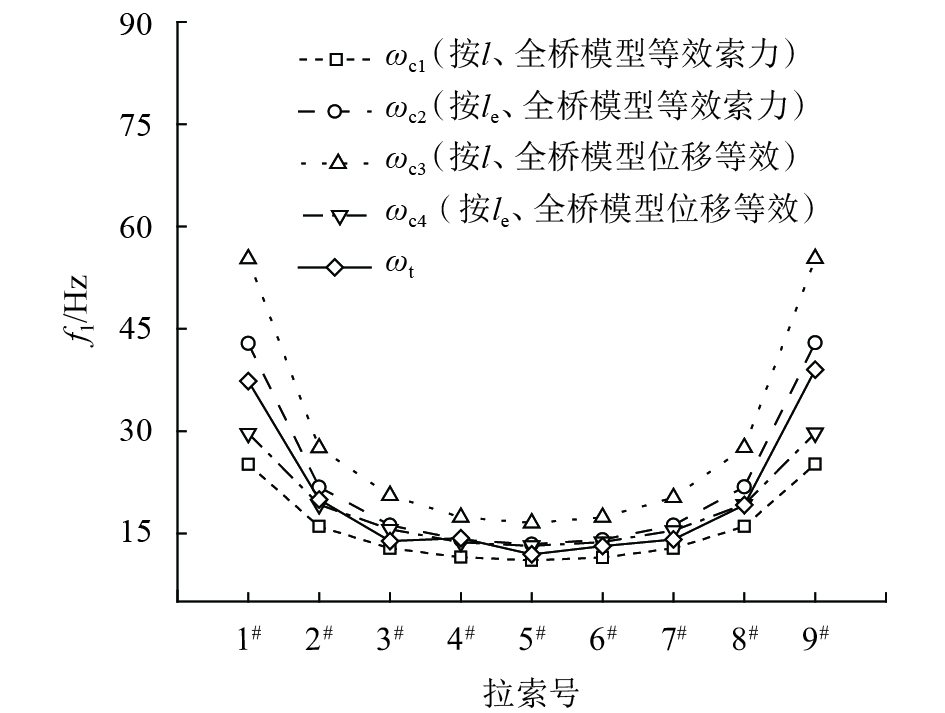 |
| 图7 拉索基频比较 Fig. 7 Comparison of cable basic frequencies |
2.5 校验系数比较
采用振动频率校验系数、索力校验系数和索力增量校验系数等3种系数对各拉索索力进行技术状况评定分析。
图8显示了3种按有效索长
 |
| 图8 3种校验系数比较 Fig. 8 Comparison of three adjustment factors |
总体情况为振动频率校验系数最大,其次为索力校验系数,索力增量校验系数最小。三者校验系数均小于1.0。对于索力增量校验系数,对于考虑抗弯刚度的影响参数
采用理论推导和试验验证相结合的理论研究方法,对拉索索力及其技术状况评定进行研究,得出了如下结论:
1)由弦振动理论和能量法推导出了索力精确求解方法,其计算结果与有限元模型计算结果吻合较好。
2)较精确求解公式法和按索端位移理论公式法确定拉索索力,本文中索力简化计算法计算结果可行。
3)通过索力、索力差和频率比较发现,由实测频率转换为实测索力过程中,应选择合理的拉索索长。在全桥有限元模型的基础上,仅分析考虑拉索自身特性时,可按索力等效的方式计算有效索长的拉索理论振动频率,这种方式与实测频率吻合较好。
4)较频率校验系数、索力校验系数和索力偏差率,索力增量校验系数对中长吊拉索索力技术状况评定验证有效且合理。
| [1] |
Nagayama T,Reksowardojo A P,Su D,et al. Bridge natural frequency estimation by extracting the common vibration component from the responses of two vehicles[J]. Engineering Structures, 2017, 150: 821-829. DOI:10.1016/j.engstruct.2017.07.040 |
| [2] |
中华人民共和国住房和城乡建设部.城市桥梁检测与评定技术规范:CJJ/T 233—2015[S].北京:中国建筑工业出版社,2015.
|
| [3] |
中华人民共和国住房和城乡建设部.建筑与桥梁结构监测技术规范:GB 50982—2014[S].北京:中国建筑工业出版社,2014.
|
| [4] |
中华人民共和国铁道部.铁路桥梁检定规范[S].北京:中国铁道出版社,2004.
|
| [5] |
赵雪峰,丁言兵,韩瑞聪,等. 基于智能手机的无线索力测量方法[J]. 振动与冲击, 2016, 35(18): 147-151. DOI:10.13465/j.cnki.jvs.2016.14.024 |
| [6] |
朱万旭,覃荷瑛,李居泽,等. 基于锚固区外置光纤光栅传感器的FAST工程拉索索力监测研究[J]. 机械工程学报, 2017, 53(17): 23-30. DOI:10.3901/JME.2017.17.023 |
| [7] |
Zheng Rui,Liu Lihua,Zhao Xia,et al. Investigation of measurability and reliability of adhesive-bonded built-in fiber Bragg grating sensors on steel wire for bridge cable force monitoring[J]. Measurement, 2018, 129(7): 349-357. DOI:10.1016/j.measurement.2018.07.053 |
| [8] |
Feng Dongming,Scarangello Thomas,Feng Maria Q,et al. Cable tension force estimate using novel noncontact vision-based sensor[J]. Measurement, 2017, 99(3): 44-52. DOI:10.1016/j.measurement.2016.12.020 |
| [9] |
Yan Banfu,Chen Wenbing,Yu Jiayong,et al. Mode shape-aided tension force estimation of cable with arbitrary boundary conditions[J]. Journal of Sound and Vibration, 2019, 440(3): 315-331. DOI:10.1016/j.jsv.2018.10.018 |
| [10] |
廖敬波,唐光武,孟利波,等. 固结拉索的一种近似频率计算公式[J]. 振动与冲击, 2013, 32(6): 149-151. DOI:10.3969/j.issn.1000-3835.2013.06.028 |
| [11] |
李素贞,Lapuerta Enrique Cavero. 基于振动测试的张弦结构拉索索力识别[J]. 振动与冲击, 2016, 35(23): 148-152. DOI:10.13465/j.cnki.jvs.2016.23.023 |
| [12] |
中华人民共和国交通部.公路斜拉桥设计细则:JTG/T D65-01—2007[S].北京:人民交通出版社,2007.
|
| [13] |
日本道路協会.道路橋示方書.同解説I共通編III コンクリート橋編[S].东京,2012.
|
| [14] |
杨咏漪,陈克坚. 大跨度铁路斜拉桥斜拉索参数振动分析[J]. 铁道工程学报, 2013, 30(10): 60-65. DOI:10.3969/j.issn.1006-2106.2013.10.013 |
| [15] |
任远,刘小玲,黄侨. 斜拉桥恒载索力长期变化趋势分析与评估[J]. 哈尔滨工业大学学报, 2015, 47(6): 103-108. DOI:10.11918/j.issn.0367-6234.2015.06.019 |
| [16] |
Du Yong,Peng Jingzhan,Richard Liew J Y,et al. Mechanical properties of high tensile steel cables at elevated temperatures[J]. Construction and Building Materials, 2018, 182(10): 52-65. DOI:10.1016/j.conbuildmlt.2018.06.012 |
| [17] |
Gao Donglai,Chen Wenli,Zhang Runtao,et al. Multi-modal vortex-and rain-wind-induced vibrations of an inclined flexible cable[J]. Mechanical Systems and Signal Processing, 2019, 118(3): 245-258. DOI:10.1016/j.ymssp.2018.08.057 |
| [18] |
武芳文,徐超,赵雷. 超大跨度斜拉桥随机地震响应参数敏感性分析[J]. 铁道学报, 2014, 36(6): 107-113. DOI:10.3969/j.issn.1001-8360.2014.06.017 |
| [19] |
张丽娜,李凤臣.大跨度桥梁斜拉索的参数振动研究[M].北京:科学出版社,2017.
|
| [20] |
张兴标,沈锐利,唐茂林,等. 悬索桥锚跨索股索力的精确计算与调整方法[J]. 西南交通大学学报, 2012, 47(4): 551-557. DOI:10.3969/j.issn.0258-2724.2012.04.003 |
| [21] |
霍学晋,高玉峰,阳洋. 蝶形拱桥的索力非线性及影响因素分析[J]. 四川大学学报(工程科学版), 2013, 45(2): 47-55. |
| [22] |
李国强,顾明,孙利民.拉索振动、动力检测与振动控制理论[M].北京:科学出版社,2014.
|
| [23] |
查利权. 基于拉索振动特征的索力检测与评估方法[J]. 振动、测试与诊断, 2014, 34(5): 967-969. DOI:10.3969/j.issn.1004-6801.2014.05.030 |
| [24] |
李强兴.拉索基本理论及应用[M].武汉:武汉大学出版社,2017.
|
| [25] |
上海市路政局.桥梁结构检测技术规程:DG/TJ08-2149—2014/J12783—2014[S].上海:同济大学出版社,2014.
|
| [26] |
中华人民共和国交通运输部.公路桥梁承载能力检测评定规程:JTG/TJ21—2011[S].北京:人民交通出版社,2011.
|
| [27] |
Hu Ting,Detection and evaluation of reinforced concrete arch bridge[D].Chengdu:Southwest Jiaotong University,2012.3. 胡婷.钢筋混凝土拱桥检测与评定[D].成都:西南交通大学,2012.3. |
| [28] |
Zhao Xiang,Effect study of cable damage to structural performance of the cable-stayed bridge[D].Nanjing:Southeast University,2005.6. 赵翔.拉索损伤对斜拉桥结构性能影响的研究[D].南京:东南大学,2005.6. |
| [29] |
淡丹辉,陈艳阳. 应用拉索频率方程修正数值解的索力识别方法[J]. 振动、测试与诊断, 2014, 34(2): 247-253. DOI:10.3969/j.issn.1004-6801.2014.02.008 |
| [30] |
日本土木学会.鋼斜張橋―技術とその変遷[R].东京, 2010.
|
| [31] |
American Association of State Highway and Transportation Officials (AASHTO).AASHTO LRFD Bridge design specifications[S].American Association of State Highway and Transportation Officials,Washington,2012.
|
| [32] |
吉林铁路线桥检测设计所,青藏铁路公司工务检测所.青藏线拉萨河特大桥常规检定评估试验[R].青藏铁路集团公司桥梁检定评估试验报告,2017.
|
| [33] |
刘震,韩小宇,张哲. 基于行波效应飞燕式钢管混凝土拱桥地震损伤分析[J]. 四川大学学报(工程科学版), 2015, 47(6): 54-60. DOI:10.15961/j.jsuese.2015.06.008 |
 2019, Vol. 51
2019, Vol. 51


