装配式混凝土结构代表了建筑结构发展的重要方向,其中楼板作为水平承重构件,成为研究的关键对象之一。相对于传统的现浇楼板,装配式混凝土叠合楼板具有施工方便、装配简单、绿色节能等优点[1],在国内的建筑行业得到了快速推广。叠合楼板预制底板与现浇层能否牢固连接是影响其力学性能的重要因素。一般认为,预制底板与现浇层间设置一定面积率的粗糙面,粗糙面的凹凸深度不小于4 mm时即可保证新旧混凝土的黏结性能[2]。由于生产工艺等因素的限制,粗糙面不易准确控制,同时工程人员也认为该种做法不够保守,因此,在工程中未被广泛使用。目前国内主要采用的是自承式钢筋桁架叠合楼板[3–6],其预制底板和现浇层间通过钢筋桁架连接,这种楼板虽然承载力较高,但钢筋用量多,造价高。为此,不同学者研发了多种形式的新型叠合板,如预制带肋混凝土叠合板、薄壁钢桁架–轻骨料混凝土叠合板、陶粒叠合层叠合板等[7–11]。作者的课题组也提出了一种带混凝土抗剪键的新型叠合板[12],通过抗剪键连接预制底板与现浇层。图1为带混凝土抗剪键的预制底板。与设置粗糙面的叠合板相比,其容易制定控制标准,整体性更高;与钢筋桁架叠合板相比,其钢筋用量低,节约成本,每平米约节约9~15元。为研究该种叠合板的力学性能,课题组首先进行了两边简支(板的一边约束竖直和水平位移,另一边约束竖直位移)且板长与板宽比值大于2的单向板的试验和理论研究,并验证了该种板在实际工程中的可行性。本文将继续进行四边简支(板的相邻两边约束竖直和水平位移,另外两边约束竖直位移)且板长与板宽比值小于2的双向板的力学性能和设计方法研究,为该类叠合板的设计提供依据。
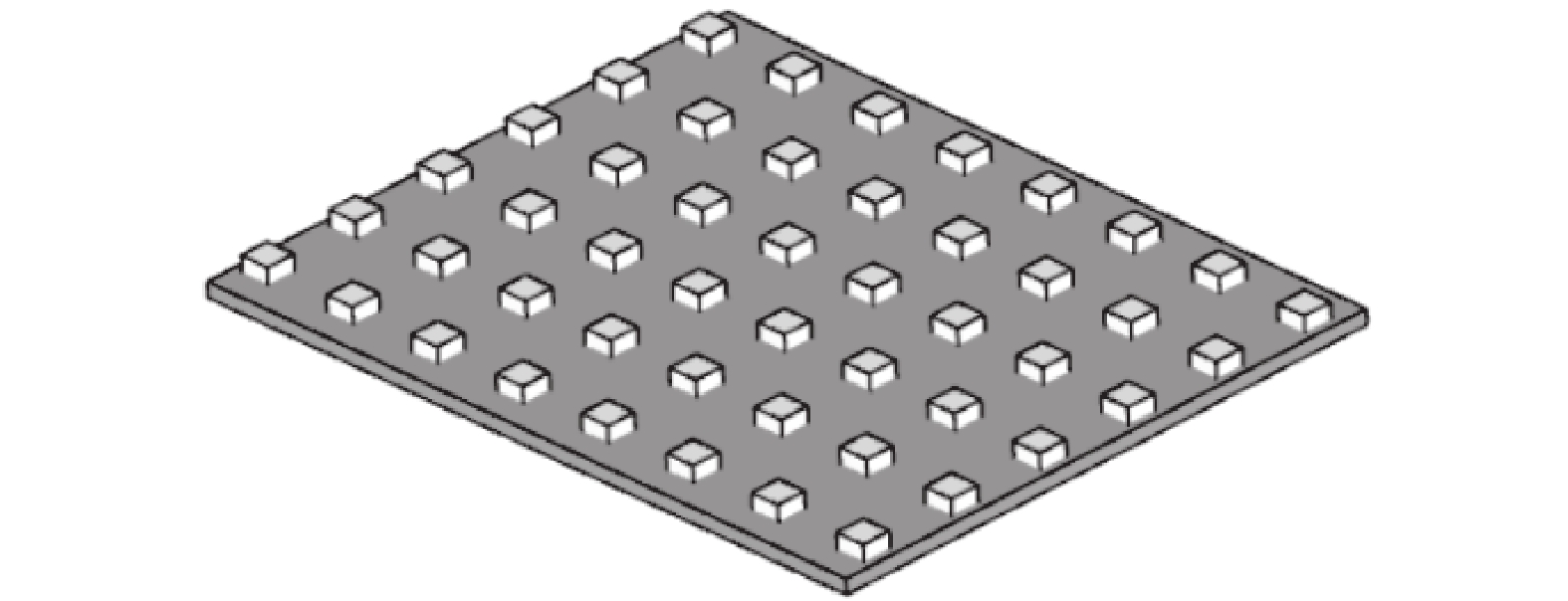 |
| 图1 带混凝土抗剪键的预制底板 Fig. 1 Precast baseplate with concrete shear keys |
1 试验研究 1.1 试件设计与制作
试验设计了2块完全相同的双向叠合板试件。试件数量少是因为课题组已完成的7块单向板试验,有限元模拟与试验结果吻合很好,本试验主要起到验证作用。设计2块叠合板,有1块作为备用试件。抗剪键的形状如图2所示,底面边长为100 mm×100 mm,高度与叠合板厚度相同,设置内凹弧边以防止预制混凝土底板和现浇层混凝土在垂直于板面的方向发生脱离。预制底板和现浇层混凝土强度均为C25,厚度均为50 mm。抗剪键混凝土的强度设计为C30,高于预制底板和现浇层混凝土强度以防止其先破坏。叠合板试件长1 960 mm,宽1 220 mm,厚100 mm。抗剪键的行间距为300 mm,列间距为450 mm。图3为板内钢筋和抗剪键的布置图,板底受力筋、分布筋和板顶构造筋均为HRB335Φ8。
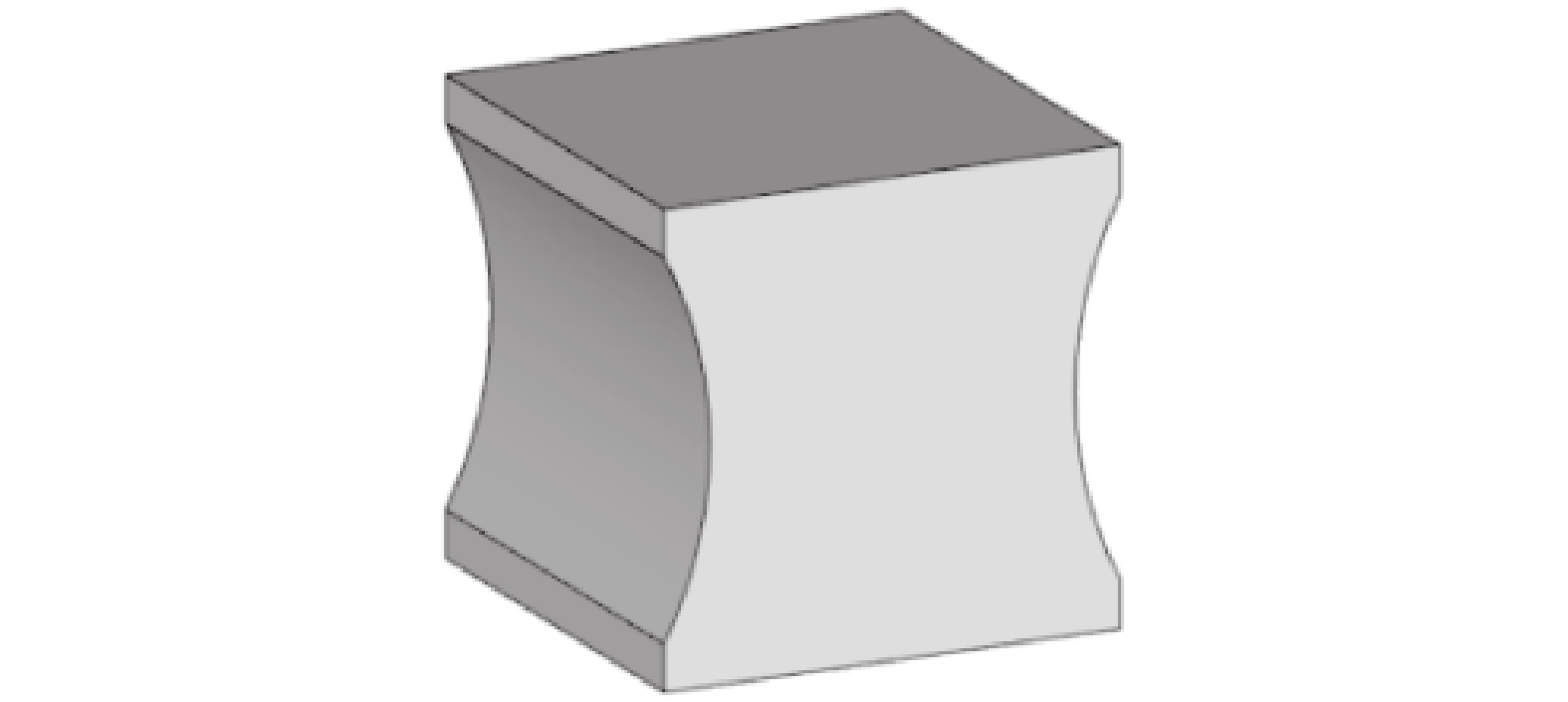 |
| 图2 抗剪键的3维模型 Fig. 2 3D model of shear key |
 |
| 图3 试件的钢筋和抗剪键布置 Fig. 3 Arrangement of steel bars and shear keys in the specimen |
在制作叠合板时,提出了3种方案:
1)使用钢制内凹模具一次反打成型,该种方法能保证抗剪键和预制底板间的整体性,但模具制作复杂,且脱模困难。
2)制作预制底板前,首先制作抗剪键,然后将抗剪键置于预制底板模板内再浇筑混凝土,该种方法较容易实现,但过程繁琐。
3)基于传统叠合结构的生产台座[13],采用滚压的方法制作带抗剪键的预制底板,该方法效率更高,适合大规模工业化生产。有关该方案的实施也是课题组目前的重点研究内容。由于最后一种方法还处于研究阶段,因此试验采用第2种方法制作叠合板试件。图4(a)为带抗剪键的预制底板,图4(b)为浇筑现浇层的带抗剪键的叠合板。实测立方体抗压强度:预制底板为21.4 MPa,抗剪键为27.6 MPa,现浇层为26.8 MPa,实测钢筋的屈服和极限强度分别为350和460 MPa。
 |
| 图4 带抗剪键叠合板的制作过程 Fig. 4 Process of making laminated slab with shear keys |
1.2 测点的布置
为测量双向板在竖向荷载作用下的竖向位移,在板底跨中中点及板长、板宽方向的四分点处布置了5个位移计,编号为W1~W5,如图5(a)所示。为测量板底受拉钢筋的应变,在板长和板宽跨中附近钢筋的中点和四分点处分别粘贴了应变片,编号为Y1~Y12,如图5(a)所示。为测量预制底板与现浇层间的相对位移,在叠合板板端的预制底板和现浇层中心分别布置了位移计,编号为W6和W7,如图5(b)所示。
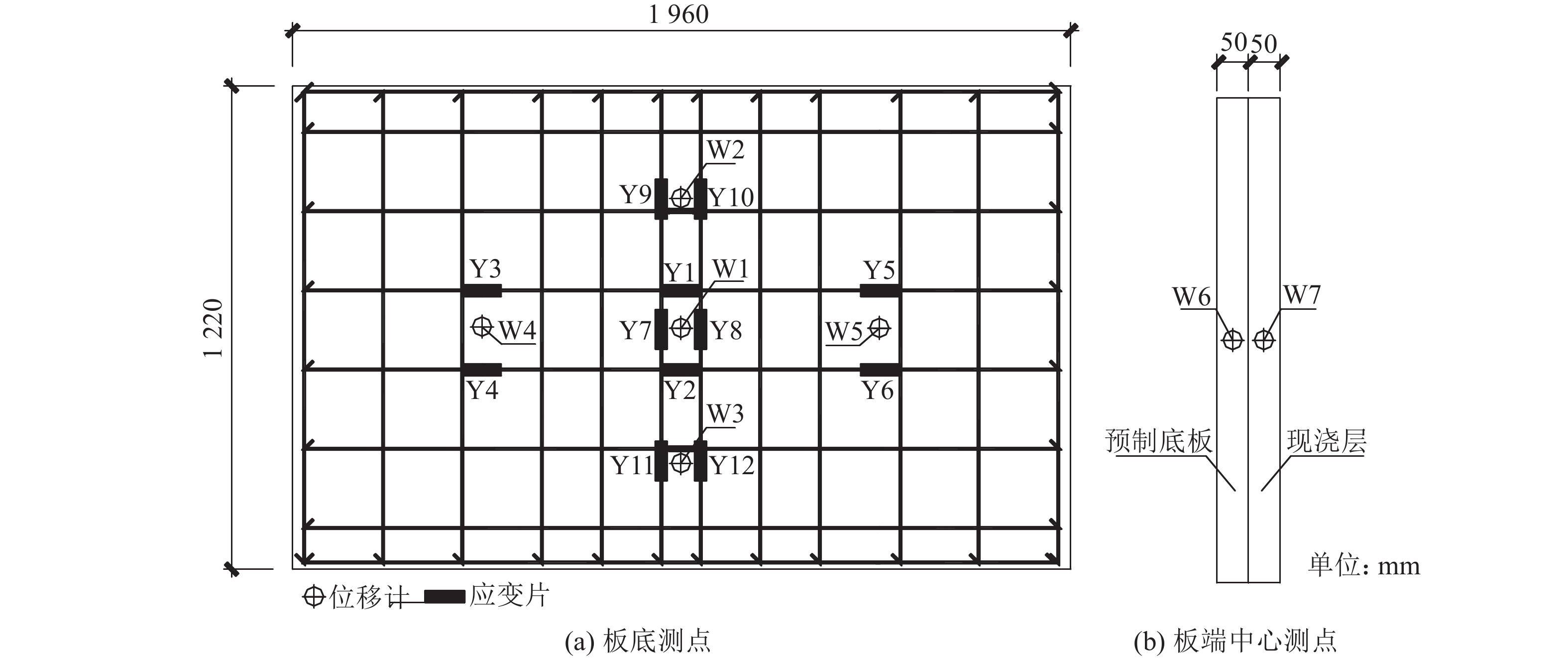 |
| 图5 位移计与应变片的位置及编号 Fig. 5 Location and number of displacement meter and strain gauge |
1.3 试验装置及加载方案设计
双向板的静载试验目前多采用沙袋或配重块等堆载方法,为防止因堆载过高而造成危险,同时也为避免因试验时间过长而产生误差积累,课题组设计了沙袋堆载与千斤顶加载组合的加载方案,通过沙袋将千斤顶施加的集中荷载扩散到楼板,如图6所示。试验中,叠合板的的相邻两端采用不动铰支座(三角形钢管支座顶部设置钢垫板,钢垫板底部沿长度方向刻三角形凹槽,扣于三角形钢柱顶部,钢垫板顶部与试件通过砂浆连接),另外相邻两端采用滚动铰支座(圆柱形钢管顶部直接放置钢垫板,钢垫板顶部与试件通过砂浆连接)。钢垫板可防止加载过程中可能因应力集中导致的支座处混凝土压碎。试验时,先在板面上堆积7层沙袋,每层8袋,每个沙袋重25 kg,然后在沙袋上放置钢垫板,最后将千斤顶作用在钢垫板上施加荷载。
 |
| 图6 双向板的试验加载装置 Fig. 6 Experimental loading system for two-way slab |
1.4 试验结果分析
试验过程中,双向板的试验现象和采集到的数据近似,因此以其中一块板的试验结果进行说明。在加载开始初期,板的变形略有增加,变化不明显。当荷载增加到47.1 kN/m2并持续一段时间后,板底开始出现第一道裂缝,裂缝宽度较细并与板宽方向大致平行。随荷载增加,裂缝数量和宽度也随之增加,裂缝先由板跨中向板长、板宽方向发展,再沿板长、板宽45°方向发展,底板最终的破坏情况如图7所示,其破坏形态符合双向板在竖向均布荷载作用下的破坏特征,说明试验采用沙袋堆载与千斤顶组合施加均布荷载的加载方案具有合理性。当荷载继续增加至125.3 kN/m2时,板跨中裂缝宽度超过1.5 mm,表明板已经破坏。
 |
| 图7 混凝土预制底板的最终破坏情况 Fig. 7 Damage at the bottom of the precast concrete slab |
叠合板在制作过程中,预制混凝土底板和抗剪键之间存在混凝土二次浇筑现象,二者间的连接牢固程度是试验重点观察的内容之一。由图7可以看出,抗剪键与预制底板之间,未出现脱开裂缝,由此说明,二者连接牢固,抗剪键与预制底板整体性很好。预制底板与现浇层混凝土间同样存在混凝土二次浇筑现象,通过布置在侧面跨中预制底板与现浇板内的水平位移计(W6和W7),测量得到二者的相对位移几乎为0。由此说明预制混凝土底板和现浇层混凝土的整体性也较好。
2 有限元模拟与分析 2.1 有限元参数选取及模拟方法验证带抗剪键双向叠合板的受力过程采用有限元软件ABAQUS模拟。模拟时混凝土的本构关系依据《混凝土结构设计规范》(GB 50010—2010)中的单轴受拉和受压应力–应变曲线计算[14–15];钢筋采用双折线模型;预制底板、抗剪键和抗剪键中的混凝土均采用C3D8R单元;钢筋均采用T3D2单元,并通过Embedded region的方式耦合在混凝土内部;模型的边界条件、加载方式及网格划分如图8所示,采用Full Newton迭代法求解。
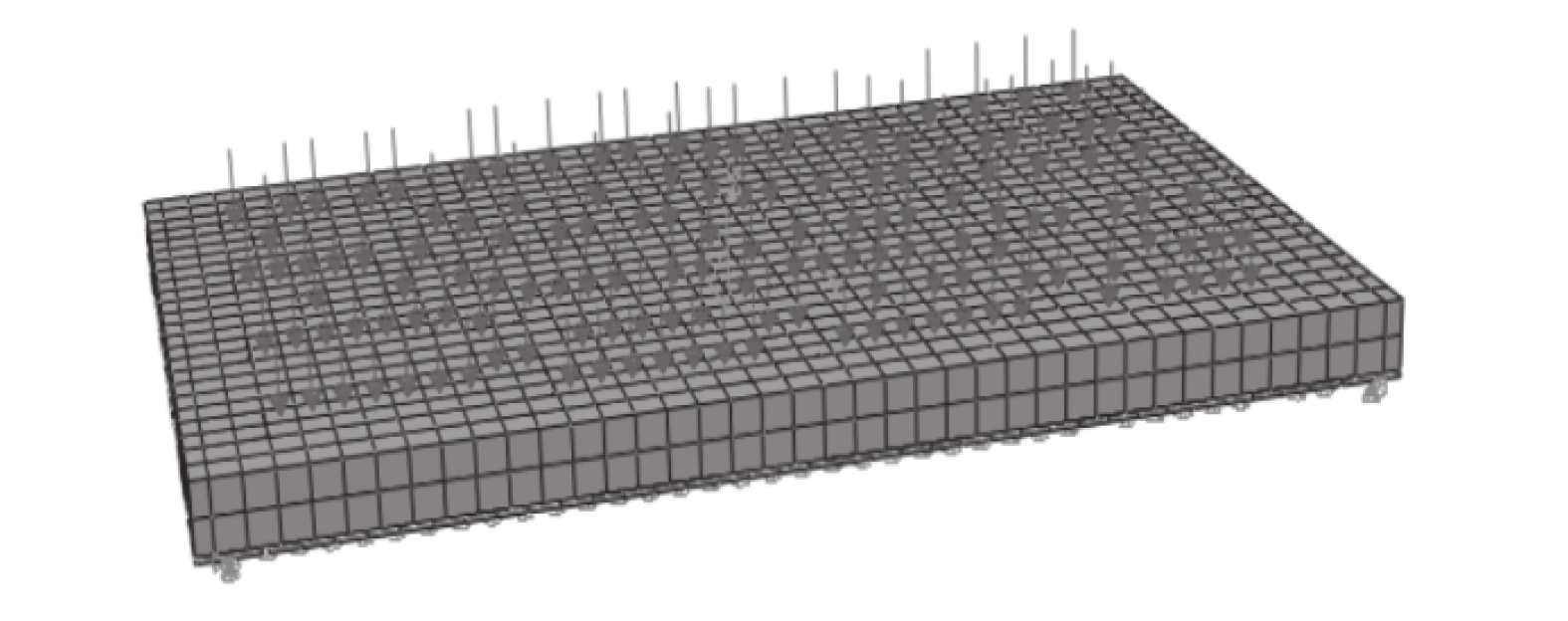 |
| 图8 模型的边界条件、加载方式及网格划分 Fig. 8 Boundary condition,loading method and mesh generation of the model |
在有限元模拟过程中,根据实际情况,叠合板抗剪键以外的预制底板与现浇层结合面间通常可采用Tie(绑定)接触和摩擦接触。若二者间连接牢固,竖向荷载作用下无相对错动,此时可采用Tie(绑定)接触;若二者间连接不牢固或存在相对错动,则采用摩擦接触,摩擦系数取0.8[16]。为验证有限元模拟的有效性,分别模拟了两种不同接触方式下双向板的受力过程,并将板跨中的荷载–位移曲线及钢筋的荷载–应变曲线模拟与试验结果进行了对比,如图9所示。其中,图9(a)中的试验曲线由编号为W1的位移计测得,图9(b)中的试验曲线是编号为Y1和Y2的应变片测得结果的平均值。
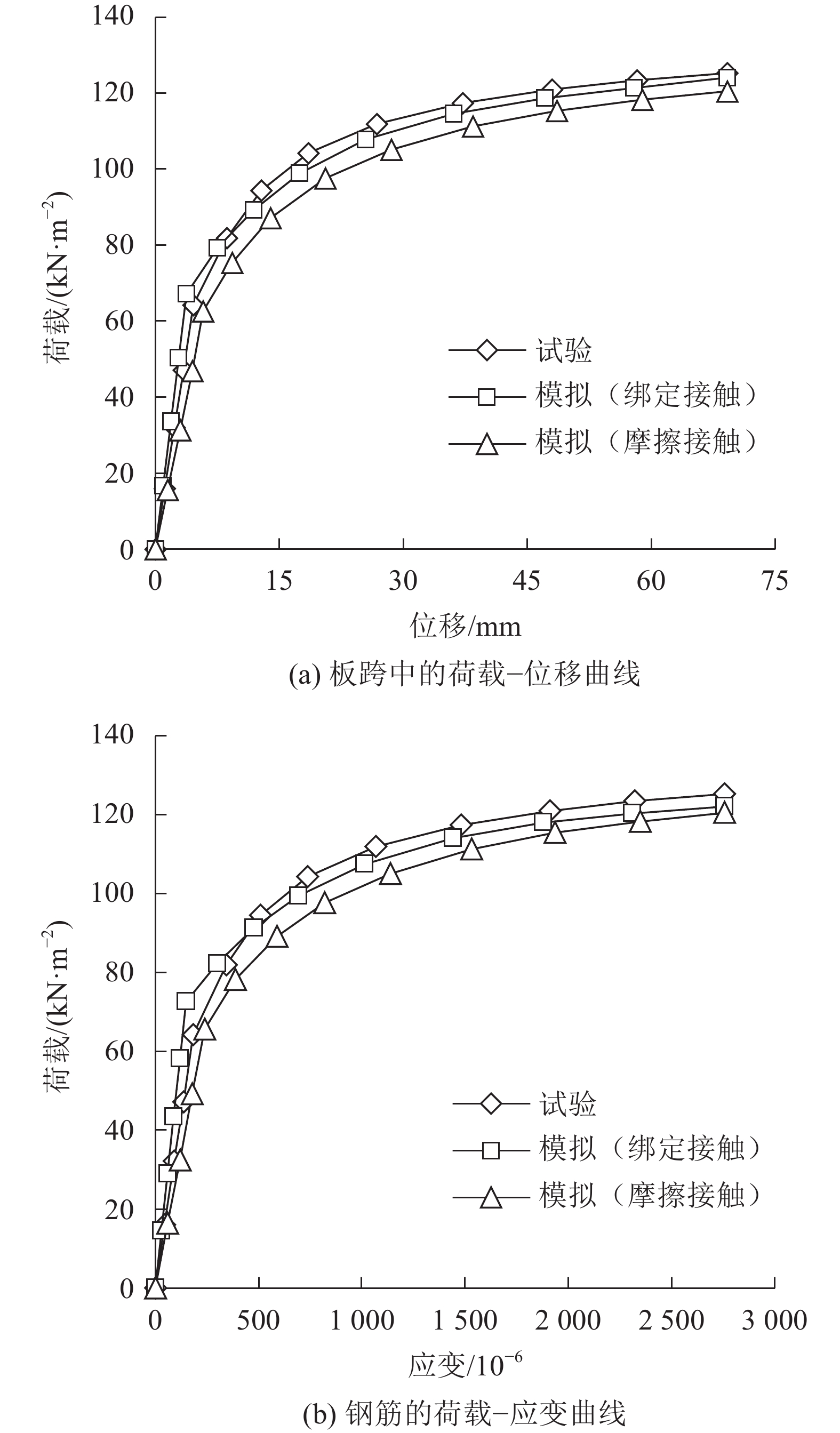 |
| 图9 模拟与试验结果对比 Fig. 9 Comparison between the simulation and the experiment results |
由图9可知,采用不同的接触方式,模拟曲线与试验曲线的变化趋势总体吻合均较好。采用Tie(绑定)接触时,板跨中的荷载–位移曲线、钢筋的荷载–应变曲线模拟结果与试验结果最大相差不足4%;采用摩擦接触时,模拟结果与试验结果最大相差不足10%。虽然预制底板与现浇板间采用Tie(绑定)接触时,模拟结果与试验结果更加接近,但在叠合板因工艺和环境等条件限制,抗剪键以外的预制底板和现浇层间未必连接牢固。为此,考虑到结构设计的可靠性,以下有限元模拟过程中,预制底板和现浇层结合面间的连接偏安全的采用摩擦接触。
2.2 双向叠合板内抗剪键的剪力分布规律四边简支双向叠合板在竖向均布荷载作用下,不同位置处的抗剪键沿X和Y方向的剪力值不同。为研究抗剪键的剪力分布规律,设计了抗剪键行间距为180 mm、列间距为360 mm,其余参数与试验相同的双向叠合板,模拟了其受力过程。
抗剪键的每个网格划分为8个基本单元,图10为位于底部1个单元的剪应力方向。X、Y、Z分别表示叠合板的长度、宽度和厚度方向,S13为YZ平面、沿Z方向的剪应力;S23为XZ平面、沿Z方向的剪应力。由垂直平面上剪应力的互等定理可知S31=S13,S32=S23,将S13和S23剪应力乘以对应的单元截面面积可得到抗剪键在结合面处沿X方向(板长)和Y方向(板宽)的总剪力。以沿X方向和Y方向的总剪力与施加于板上的竖向均布荷载为坐标绘制荷载与总剪力间的关系曲线。因在竖向均布荷载的作用下,四边简支叠合板内沿X和Y方向的抗剪键分布对称,剪力分布规律相同,仅选取叠合板1/4区域内的抗剪键分析抗剪键剪力分布规律。抗剪键的编号如图11所示。
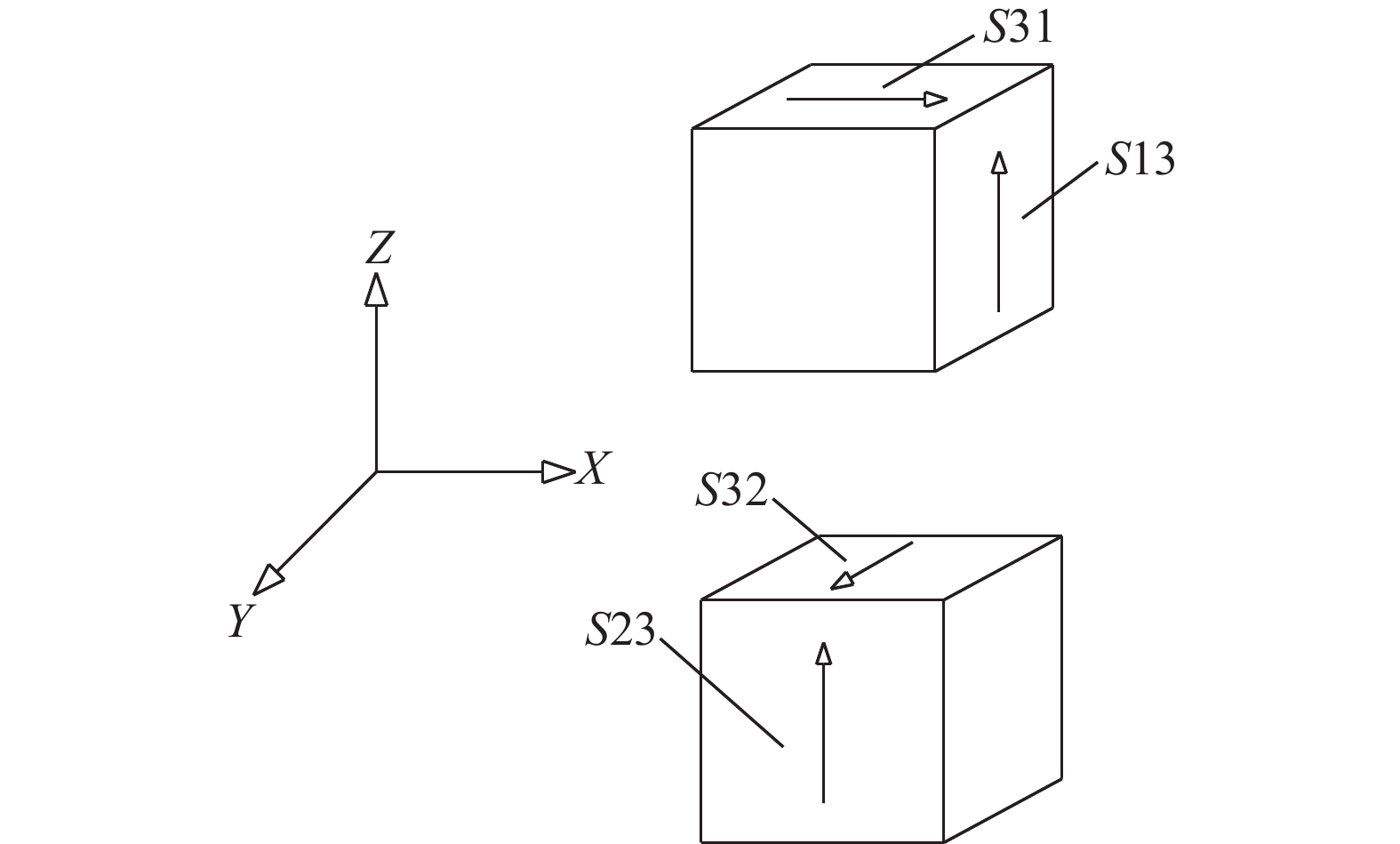 |
| 图10 抗剪键1个单元内的剪应力方向 Fig. 10 Shear stress direction in one unit of shear key |
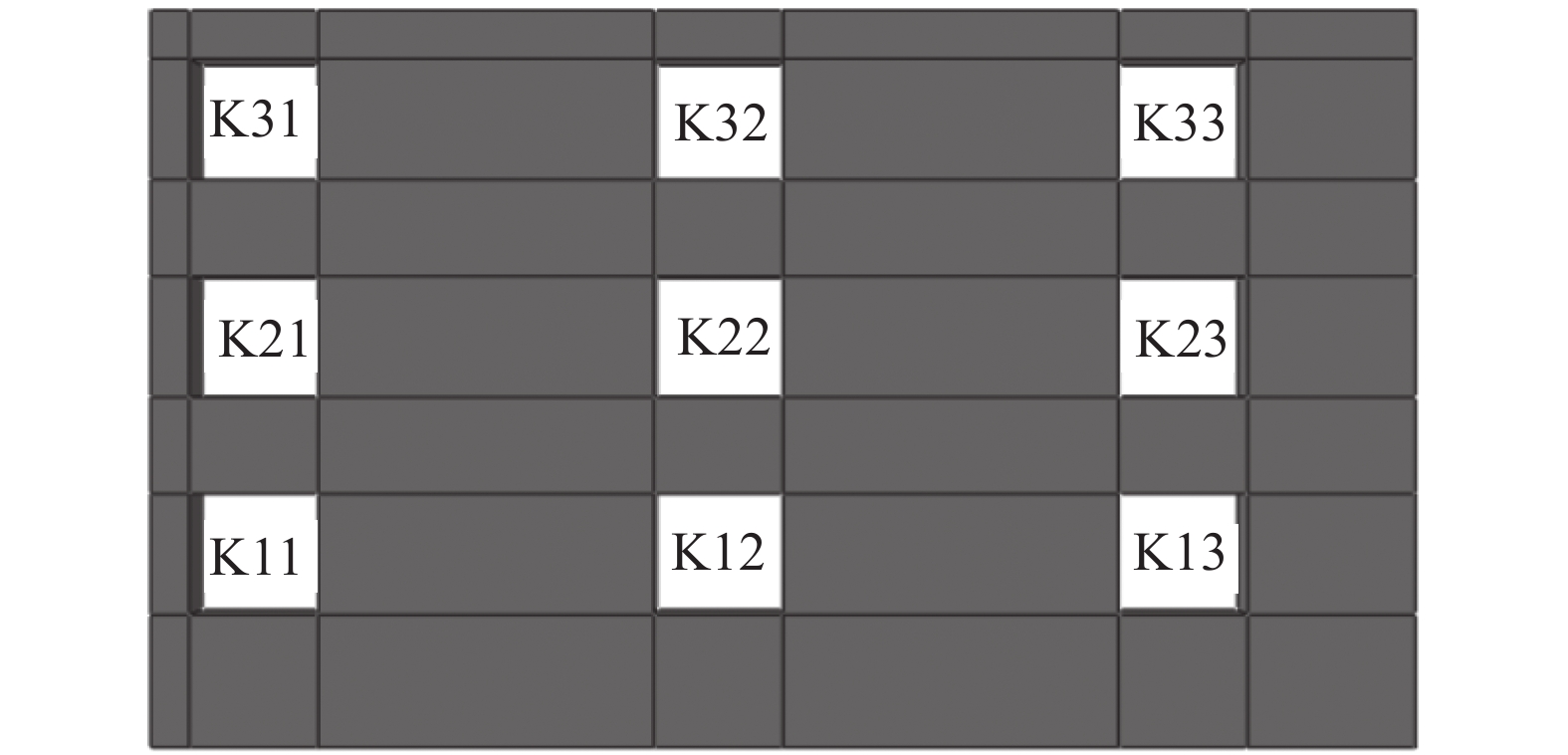 |
| 图11 叠合板1/4区域内的抗剪键编号 Fig. 11 Shear keys number in the 1/4 area of the laminated slab |
图12为抗剪键K11~K13、K21~K23和K31~K33沿X方向的荷载–剪力曲线。由图12可知,3组抗剪键的剪力均随竖向荷载的增加而线性增加,当抗剪键的剪力增加至某一最大值后突然下降,表现为曲线斜率的方向突然改变、斜率的绝对值突然增大,由此说明抗剪键的破坏为脆性破坏。
 |
| 图12 3组抗剪键沿X方向的荷载–剪力曲线 Fig. 12 Load–shear force curves of three groups of shear keys along the X direction |
表1为各抗剪键沿X方向的最大剪力值、达到最大剪力的顺序(破坏顺序)及对应的钢筋应力、板底混凝土拉应力和施加于板顶的竖向荷载。从表1可以看出,3组抗剪键的最大剪力值不同,靠近板跨中位置处(K13、K23、K33)最小,靠近支座位置处(K11、K21、K31)最大,这主要是因为跨中抗剪键受弯矩和剪力的耦合作用。
| 表1 抗剪键的最大剪力及对应的竖向荷载等 Tab. 1 Maximum shear force of shear keys and the corresponding vertical load etc. |
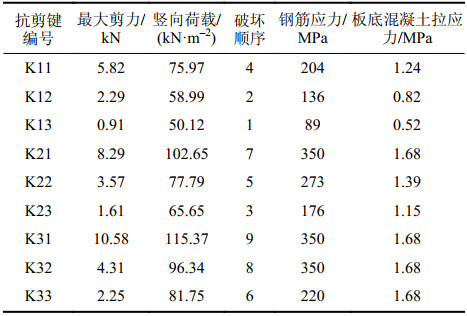 |
由图11和表1也可知,抗剪键的破坏从K13开始,当发展到斜对角线顶部的K33后,板底混凝土达到抗拉强度,混凝土开裂,继续发展到K21时,钢筋达到屈服应力,叠合板破坏。由此说明抗剪键的破坏并非同时发生,部分抗剪键破坏不会导致叠合板的破坏,只有当其破坏数量达到一定程度后,叠合板才发生破坏。
叠合板在Y方向分布的3组抗剪键K11~K31、K12~K32和K13~K33,沿Y方向与沿X方向的剪力分布规律类似。为分析同一位置处的抗剪键沿X、Y方向的剪力分布规律,对比了抗剪键K11、K22和K33沿X方向与Y方向的荷载–剪力曲线,如图13所示。从图13中可看出:3块抗剪键在Y方向的最大剪力均大于在X方向的最大剪力,且Y方向的剪力先达到最大值,这是因为在竖向均布荷载的作用下,双向板在短跨X方向所受弯矩大于长跨Y方向,抗剪键在Y方向上受到的弯矩影响更大。由此说明在设计带抗剪双向叠合板时,沿短跨方向布置的抗剪键间距不宜过大。
 |
| 图13 不同抗剪键沿X、Y方向的荷载–剪力曲线对比 Fig. 13 Comparison among the load–shear force curves of different shear keys along theX and Y direction |
2.3 双向叠合板的力学性能影响因素分析
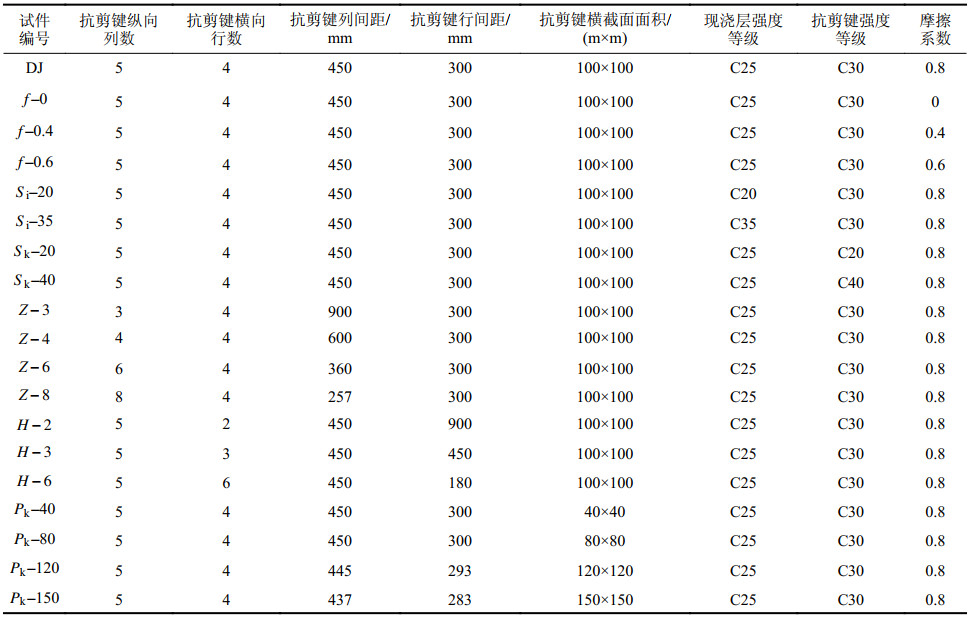
为分析不同因素对叠合板荷载–位移曲线的影响,共设计了19块叠合板,如表2所示。表2中:标准板编号为DJ,混凝土强度等级为C30,预制底板和现浇层混凝土强度等级为C25;板内配筋为HRB335Φ8@200。其余编号的板,字母表示与标准板不同的参数,数字为该参数数值,如编号为
| 表2 叠合板设计参数 Tab. 2 List of designed laminated slabs |
 |
 |
|
图14 摩擦系数
|
 |
|
图15 |
 |
|
图16 抗剪键混凝土强度等级
|
 |
|
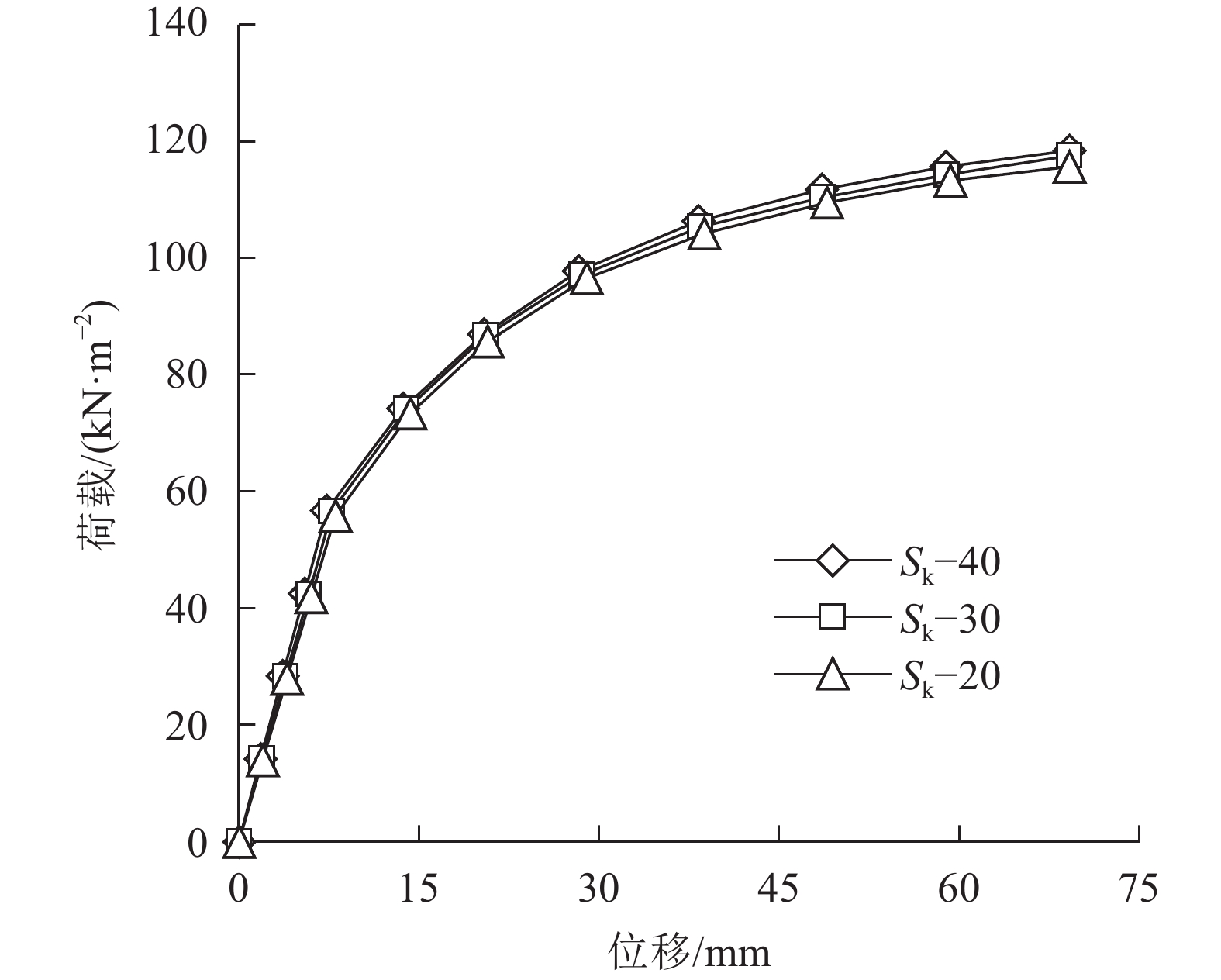
图17 抗剪键列数
|
 |
| 图18 抗剪键行数H不同时叠合板的荷载–位移曲线 Fig. 18 Load–displacement curves of the laminated slabs with different row number of shear keyH |
 |
|
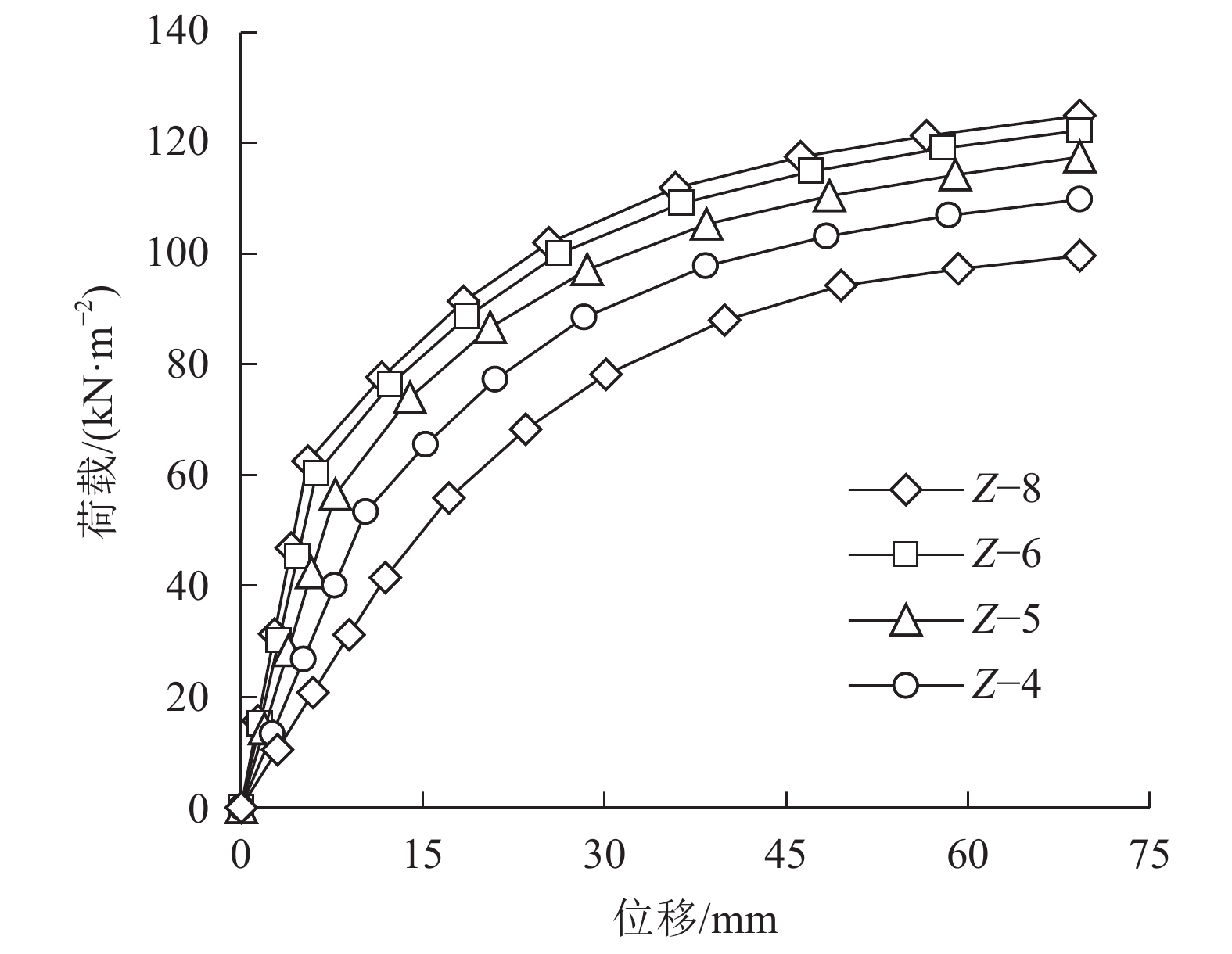
图19 抗剪键横截面面积
|
图14为其他参数不变,结合面间摩擦系数分别为0、0.4、0.6和0.8时,双向叠合板的荷载–位移曲线,对应各叠合板的屈服荷载分别为77.1、77.3、77.7和78.2 kN/m2,对应的屈服位移分别为16.6、16.5、16.3和16.1 mm。由图14可看出:由于抗剪键的存在,结合面摩擦系数不同的双向叠合板荷载–位移曲线几乎重合,改变叠合板摩擦系数对叠合板的屈服荷载和屈服位移影响很小,当摩擦系数由0增加到0.8时,叠合板的屈服强度仅上升了1.4%,对应的屈服位移相应仅下降了3%。出现这种现象的原因在于:当布置的抗剪键达到一定数量后,可有效降低预制底板和现浇层间的相对错动。由此说明,布置一定数量抗剪键的双向叠合板,改变结合面摩擦系数对其力学性能几乎无影响。
图15为其他参数不变,现浇层混凝土强度等级分别为C20、C25和C35时,双向叠合板的荷载–位移曲线,对应的屈服荷载分别为77.4、78.2和79.2 kN/m2,屈服位移分别为15.9、16.1和16.4 mm。
从图15可看出:现浇层混凝土强度等级不同的双向叠合板荷载–位移曲线几乎重合,改变现浇层混凝土强度等级对叠合板的屈服荷载和屈服位移影响很小,当现浇层混凝土强度等级由C20增加到C35时,叠合板的屈服强度仅上升了2.3%,对应的屈服位移相应仅下降了3.2%。出现这种现象的原因在于:当叠合板的厚度较小时,受压区高度也较小,不同强度的现浇层混凝土对板的屈服强度提高不明显。因此,在设计过程中,对于使用厚度较小的叠合板,可仅要求其现浇层混凝土强度等级不低于预制层混凝土强度等级。
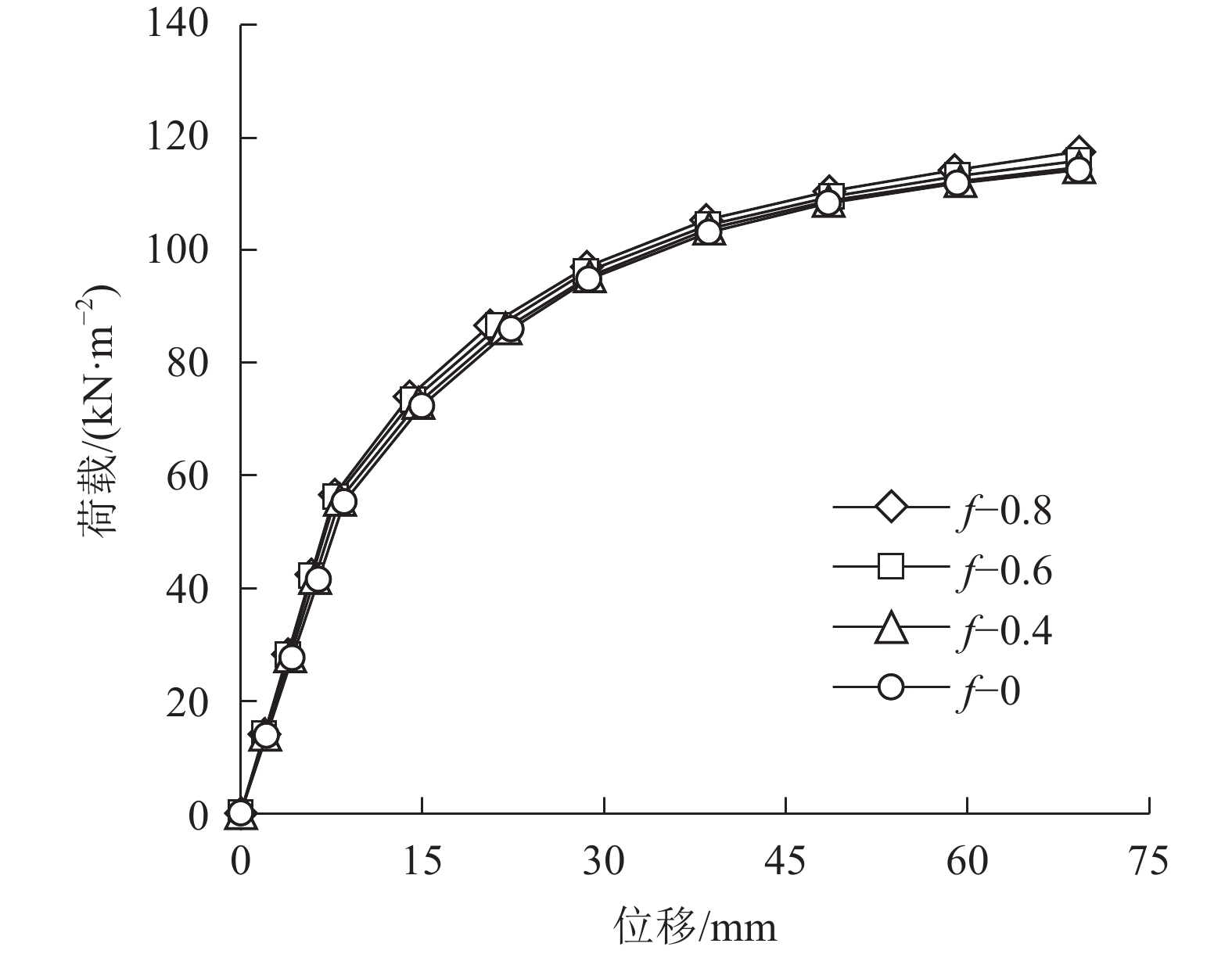
图16为其他参数不变,抗剪键混凝土强度等级分别为C20、C30和C40时,双向叠合板的荷载–位移曲线,对应的屈服荷载分别为77.8、78.2和78.8 kN/m2,屈服位移分别为16.3、16.1和15.9 mm。从图16可看出:抗剪键混凝土强度等级不同的双向叠合板荷载–位移曲线几乎重合,改变抗剪键混凝土强度等级对叠合板的屈服荷载和屈服位移影响很小,当抗剪键混凝土强度等级由C20增加到C40时,叠合板的屈服强度仅上升了1.3%,对应的屈服位移相应仅下降了2.5%。由此说明:抗剪键混凝土强度等级对叠合板的力学性能几乎无影响。在设计过程中,抗剪键可采用与叠合板强度等级相同的混凝土制备。
图17为其他参数不变,抗剪键的列数分别为3、4、5、6和8时,双向叠合板的荷载–位移曲线,对应的屈服荷载分别为70.3、74.6、78.2、80.6和81.6 kN/m2,屈服位移分别为23.4、19.3、16.1、13.9和12.4 mm。从图17可看出:抗剪键纵向列数增加,叠合板的屈服荷载增大,屈服位移减小。当抗剪键纵向列数由3增加至8时,叠合板屈服荷载增加了16.1%,屈服位移减小了47%;当抗剪键纵向列数由6增加至8时,叠合板屈服荷载增加了1.2%,屈服位移减小了10.8%。由此说明,仅考虑结合面间摩擦接触时,随抗剪键纵向列数的增加,叠合板的屈服荷载增加,屈服位移减小,但当抗剪键纵向列数增加至一定程度后,这种变化趋势不再明显。
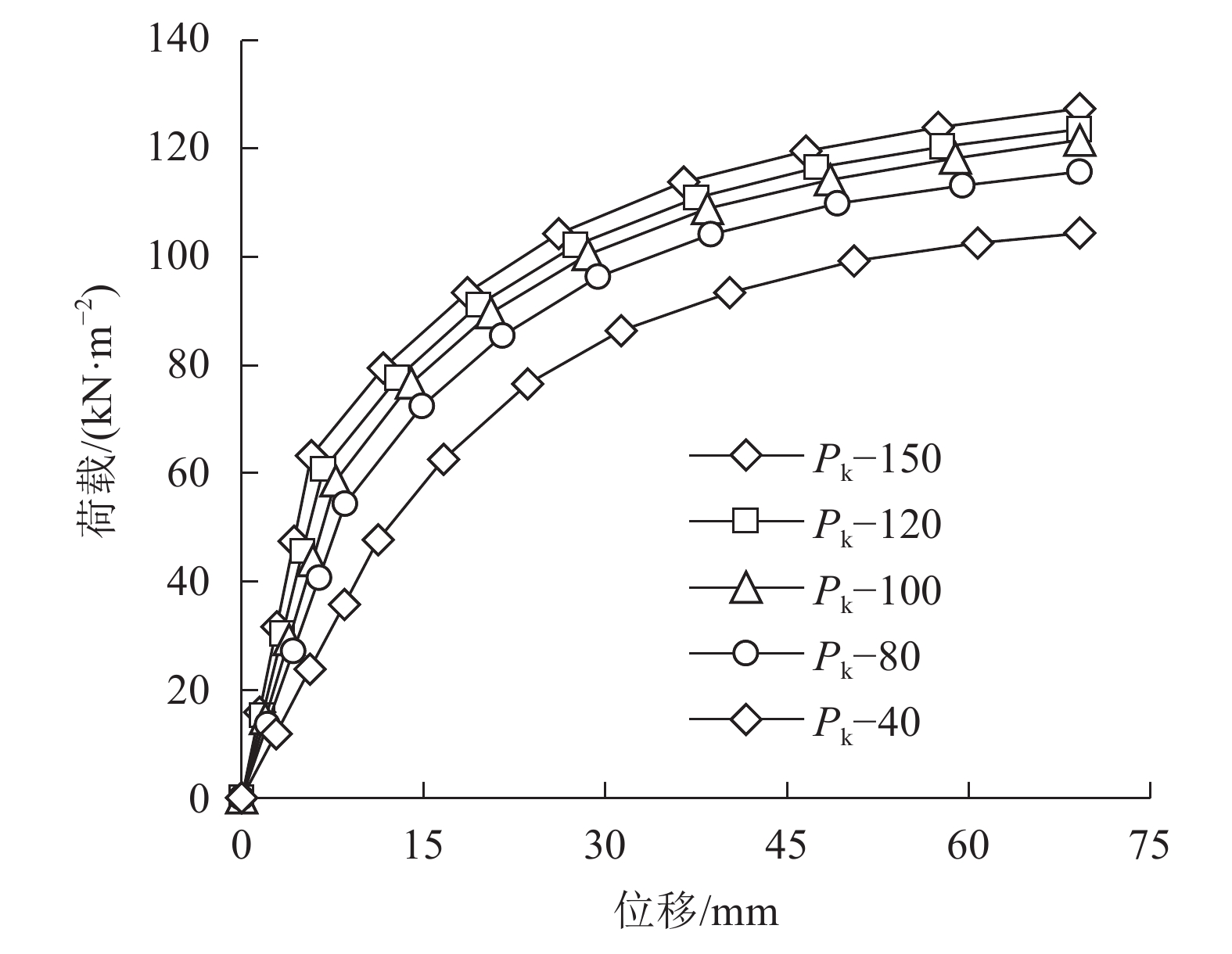
图18为其他参数不变,抗剪键的行数分别为2、3、4和6时,双向叠合板的荷载–位移曲线,对应的屈服荷载分别为72.3、75.6、78.2和79.4 kN/m2,屈服位移分别为22.3、18.1、16.1和14.9 mm。
从图18可看出:抗剪键行数增加,叠合板的屈服荷载增大,屈服位移减小。当抗剪键横向行数由2增加至6时,叠合板屈服荷载增加了9.8%,屈服位移减小了33.2%;当抗剪键行数由4增加至6时,叠合板屈服荷载增加了1.5%,屈服位移减小了7.5%。由此说明,仅考虑板结合面间摩擦接触时,随抗剪键行数增加,叠合板的屈服荷载增加,屈服位移减小,但当抗剪键行数增加至一定程度后,这种变化趋势不再明显。同时,与抗剪键列数的变化相比,行数的改变对叠合板承载力的影响相对较小。
图19为其他参数不变,抗剪键在结合面处的横截面面积分别为40×40、80×80、100×100、120×120和150×150 mm2时,双向叠合板的荷载–位移曲线,对应的屈服荷载分别为70.5、75.3、78.2、79.5和80.9 kN/m2,屈服位移分别为23.1、18.7、16.1、15.2和12.9 mm。从图19可看出:抗剪键横截面面积增加,叠合板的屈服荷载增大,屈服位移减小。当抗剪键横截面面积由40×40 mm2增加至150×150 mm2时,叠合板屈服荷载增加了14.8%,屈服位移减小了44%;当抗剪横截面面积超出一定值时,这种变化趋势不再明显,如抗剪键横截面面积由120×120 mm2增加至150×150 mm2时,叠合板屈服荷载仅增加了1.8%,屈服位移减小了1.5%。由此说明,仅考虑结合面间摩擦接触时,随抗剪键横截面面积增加,叠合板的屈服荷载增加,屈服位移减小,但当抗剪键横截面面积增加到一定程度后,这种变化趋势不再明显。
3 双向叠合板屈服弯矩及屈服位移简化计算式有限元模拟的方法过于繁琐,在实际工程中应用不便。为此,建立带抗剪键双向叠合板的屈服弯矩和屈服位移简化计算式。第2节研究表明,抗剪键列数、行数和横截面面积是影响双向叠合板力学性能的主要因素,为便于回归,采用抗剪键面积率
| $ {M_{{\rm a} {{x}}}} = {R_{\rm{m}}}(a) \cdot {M_{{x}}} $ | (1) |
| $ {M_{{\rm a}{{y}}}} = {R_{\rm{m}}}(a) \cdot {M_{{y}}} = {R_{\rm{m}}}(a) \cdot \left( {\mu {M_{{x}}}} \right) $ | (2) |
| $ {D_{\rm a}} = {R_{\rm{d}}}(a) \cdot D $ | (3) |
式中:
根据式(1)和(2),已知现浇板的屈服弯矩,可求得同条件下不同抗剪键面积率的叠合板对应的屈服弯矩;根据式(3),已知现浇板的屈服位移,可求得同条件下不同抗剪键面积率的叠合板对应的屈服位移。
回归
| 表3 回归数据 Tab. 3 Regression data |
 |
表3中,试件为表2中部分试件,
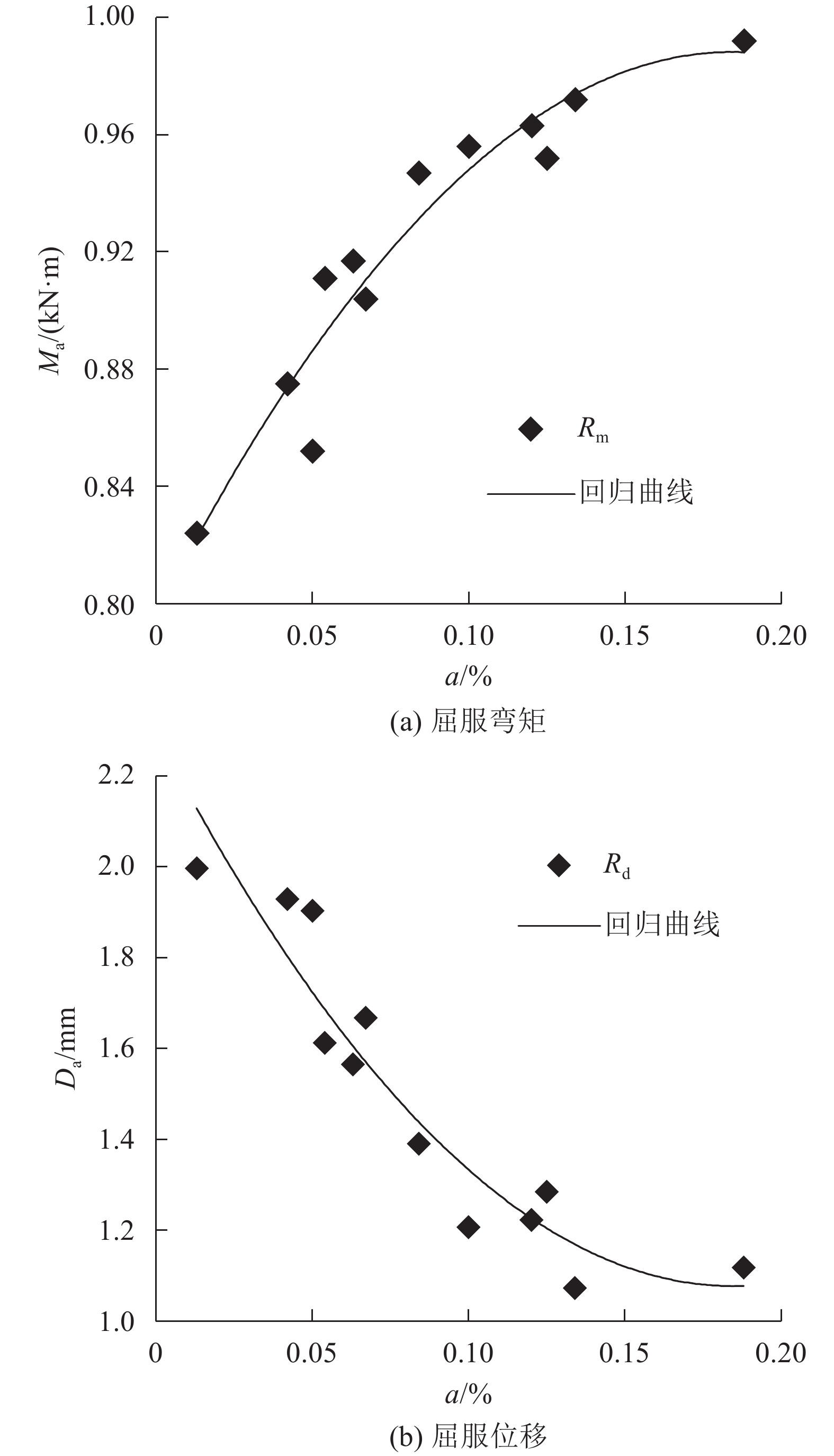 |
| 图20 叠合板屈服弯矩和屈服位移修正系数拟合曲线 Fig. 20 Regression curves of the correction coefficient of yield capacity and yield deflection of laminated slab |
| $ {R_{\rm{m}}} = - 7.49{a^2} + 2.46a + 0.78 $ | (4) |
| $ {R_{\rm{d}}} = 35.64{a^2} - 13.17a + 2.29 $ | (5) |
简化计算式的判定系数R2分别为0.92和0.90,表明数值间的拟合规律较好。
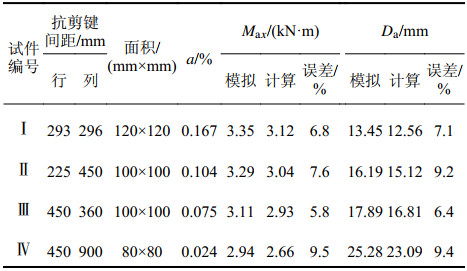
为验证简化计算式的有效性,随机设计了4块面积不同的双向叠合板,分别采用有限元模拟和简化计算式,计算了各板的屈服弯矩和屈服位移,结果见表4。由表4可知,简化计算式的计算结果与模拟结果相差不足10%,验证了简化计算式的有效性。
| 表4 两种方法的计算结果对比 Tab. 4 Comparison between the results from two methods |
 |
工程应用时,可先按现浇板的设计方法确定叠合板的几何尺寸和配筋,再计算现浇板的屈服弯矩
基于试验和有限元模拟方法,分析了四边简支双向带抗剪混凝土叠合板在竖向均布荷载作用下,抗剪键的剪力分布规律及力学性能影响因素,提出了屈服弯矩和屈服位移简化计算式,主要结论如下:
1)采用堆载与千斤顶施加等效均布荷载的加载方案具有一定的合理性,预制底板与抗剪键间、预制底板与现浇层混凝土间虽然存在混凝土二次浇筑现象,但整体性仍然较好。
2)竖向均布荷载作用下,四边简支双向叠合板抗剪键的剪力均随竖向荷载的增加而线性增加,当增加至某一最大值时突然下降,抗剪键表现为脆性破坏。抗剪键的破坏并非同时发生,部分抗剪键破坏不会导致叠合板的破坏,只有当其破坏数量达到一定程度后,叠合板才发生破坏。
3)叠合板的结合面间设置为摩擦接触时,抗剪键行数、列数及横截面面积增加,叠合板的屈服荷载增加,屈服位移减小,且抗剪键行数改变较列数改变影响小;当三者增加至一定程度后,影响不再明显。布置一定数量抗剪键的叠合板,现浇层及抗剪键混凝土强度等级、结合面摩擦系数对屈服荷载和屈服位移几乎无影响。
4)建立的带抗剪键混凝土叠合板的屈服弯矩和屈服位移简化计算式,计算结果偏于安全,可供实际工程参考应用。
| [1] |
Wang Jun,Zhao Jida,Hu Zongyu. Review and thinking on development of building industrialization in China[J]. China Civil Engineering Journal, 2016, 4(9): 1-8. [王俊,赵基达,胡宗羽. 我国建筑工业化发展现状与思考[J]. 土木工程学报, 2016, 4(9): 1-8. DOI:10.15951/j.tmgcxb.2016.05.001] |
| [2] |
中国城乡建设部.装配式混凝土结构技术规程:JGJ1—2014[S].北京:中国建筑工业出版社,2014.
|
| [3] |
Ma Lan,Chen Xiangrong,Jiang Lu,et al. Experimental research and finite element analysis of concrete floor slabs with steel bar truss[J]. Building Structure, 2013, 43(21): 54-57. [马兰,陈向荣,蒋璐,等. 钢筋桁架混凝土叠合楼板试验及有限元分析[J]. 建筑结构, 2013, 43(21): 54-57. DOI:10.19701/j.jzjg.2013.21.012] |
| [4] |
Lu Jiasen,Xu Haibing,Zheng Zhenpeng. Design method for reinforcement truss concrete composite slab[J]. Building Structure, 2016, 4(18): 99-103. [卢家森,徐海兵,郑振鹏. 钢筋桁架混凝土叠合楼板设计方法[J]. 建筑结构, 2016, 4(18): 99-103. DOI:10.19701/j.jzjg.2016.18.020] |
| [5] |
Wang B. Study on flexural bearing capacity of unbounded pre-stressing composite slab[J]. Applied Mechanics and Materials, 2011, 71(1): 1020-1024. DOI:10.4028/www.scientific.net/AMM.71-78.1020 |
| [6] |
Chou C C,Chen J H. Development of floor slab for steel post-tensioned self-centering moment frames[J]. Journal of Constructional Steel Research, 2011, 61(10): 1621-1635. DOI:10.1016/j.jcsr.2011.04.006 |
| [7] |
Zhang Jingsong,Ni Yongshu,Yao Yuan,et al. In-plane mechanical property of superimposed concrete slab with precast ribbed panels jointed in different directions[J]. China Civil Engineering Journal, 2015, 48(5): 23-34. [张敬松,倪永书,姚远,等. 不同拼缝方向的预制带肋底板混凝土叠合板面内受力性能[J]. 土木工程学报, 2015, 48(5): 23-34. DOI:10.15951/j.tmgcxb.2015.05.003] |
| [8] |
Wang Xintang,Tong Hailun,Xu Jincan. Experimental study on post-fire mechanical property of thin-walled steel truss-ceramsite laminated slabs[J]. Journal of Natural Disasters, 2016, 25(2): 128-138. [王新堂,童海伦,徐金灿. 薄壁钢桁架–轻骨料混凝土叠合板火灾后受力性能试验研究[J]. 自然灾害学报, 2016, 25(2): 128-138. DOI:10.13577/j.jnd.2016.0215] |
| [9] |
Jiang Xinliang,Yue Jianwei. Bearing capacities of ceram site concrete composite slab with trough bottom plate[J]. Journal of Sichuan University(Engineering Science Edition), 2006, 38(6): 6-11. [姜忻良,岳建伟. 陶粒叠合层叠合板的承载能力研究[J]. 四川大学学报(工程科学版), 2006, 38(6): 6-11. DOI:10.15961/j.jsuese.2006.06.002] |
| [10] |
Thanoon W A,Yardim Y,Jaafar M S,et al. Development of interlocking mechanism for shear transfer in composite floor[J]. Construction and Building Materials, 2010, 24(12): 2604-2611. DOI:10.1016/j.conbuildmat.2010.05.015 |
| [11] |
Mark N,Amir F. Structural GFRP permanent forms with T-shape ribs for bridge decks supported by precast concrete girders[J]. Journal of Bridge Engineering, 2013, 18(9): 813-826. DOI:10.1061/(ASCE)BE.1943-5592.0000418 |
| [12] |
李明,赵唯坚,王振,等.易连接带抗剪键混凝土叠合楼板结构:CN201721303294[P].2018–06–22.
|
| [13] |
Xiao Jingping. Production process of prestressed high-strength superimposed beam[J]. Architecture Technology, 2014, 4(1): 53-55. [肖景平. 预应力高强叠合结构叠合梁生产工艺[J]. 建筑技术, 2014, 4(1): 53-55. DOI:10.13731/j.issn.1000-4726.2014.01.013] |
| [14] |
中国城乡建设部.混凝土结构设计规范:GB 50010—2010[S].北京:中国建筑工业出版社,2015.
|
| [15] |
Gao Xiangling,Zhang Yeshu,Li Jie. Numerical simulation of a RC frame based on ABAQUS beam elements[J]. Structural Engineers, 2013, 29(6): 19-26. [高向玲,张业树,李杰. 基于ABAQUS梁单元的钢筋混凝土框架结构数值模拟[J]. 结构工程师, 2013, 29(6): 19-26. DOI:10.15935/j.cnki.jggcs.2013.06.009] |
| [16] |
Chen Fuqiang,Tian Wei,Liu Zhanguo,et al. Experiment study on friction coefficient of concrete with matching pouring surface[J]. China Harbor Engineering, 2014(12): 34-38. [陈富强,田唯,刘占国,等. 匹配浇筑混凝土接触面摩擦系数试验研究[J]. 中国港湾建设, 2014(12): 34-38. DOI:10.7640/zggwjs201412008] |
 2019, Vol. 51
2019, Vol. 51

