风化花岗岩广泛分布于中国华南地区[1],强风化程度以上花岗岩遇水易崩解,水稳定性极差[2]。工程实践表明,全风化花岗岩在工程扰动后遇水崩解是交通隧道等地下工程建设中发生突水突泥灾害的主要原因[3-4]。
针对风化花岗岩的崩解特性,相关学者进行了大量研究工作,并取得一定成果。张抒等[5]利用自制仪器进行崩解试验,从微观角度将土颗粒的粒间受力状态进行简化分析,继而对非饱和花岗岩残积土的崩解机制进行分析;李建新等[6]通过自制崩解仪对不同失水方式的全风化花岗岩试样的遇水崩解特性进行了系统研究;谭鉴益[7]对广西岩溶塌陷区的原状土及扰动土的崩解机理进行了分析,认为土体中蒙脱石含量、微观结构、粒径分布、初始含水率及酸碱条件等因素均与土的崩解相关。
注浆作为提高岩土体物理力学性能的主要技术手段之一,被广泛应用于全风化花岗岩地层的灾害防治领域[8-9]。已有研究表明该类地层以劈裂注浆为主,目前以浆液扩散机制及注浆固结体力学性能为主。崔红琴[10]研究了注浆等加固手段对全风化花岗岩围岩变形的影响;郭小红[11]、李蓉[12]等以厦门翔安隧道为工程背景,分析了注浆材料、注浆参数及注浆工艺对全风化花岗岩加固效果的作用规律;张顶立等[13]研究了全风化花岗岩地层的注浆加固机理,并提出复合注浆关键技术及评价指标;李相辉等[14]研究了不同充填介质断层破碎带的注浆加固机理。
目前,在全风化花岗岩注浆加固方面的研究,多以注浆加固模式、力学强度提升幅度等方面为主,缺乏对注浆后全风化花岗岩抗崩解特性的研究,针对全风化花岗岩抗崩解特性提高的注浆参数设计方法方面,仍缺乏科学系统的理论和方法。基于响应面法,通过注浆模拟试验,揭示了注浆后全风化花岗岩土体抗崩解特性及抗压强度的影响因素,提出应用于全风化花岗岩地层注浆治理的参数设计方法,并通过工程现场加以验证,以期为全风化花岗岩地层的注浆加固治理提供一定理论指导。
1 试验材料与方法 1.1 全风化花岗岩选取广西岑溪均昌隧道全风化花岗岩段DK7+825(DK为右洞)作为取样点进行原位取样,根据《土工试验规程》(SL237—199)对全风化花岗岩的基础物理特性进行测试,土体相关参数见表1。
| 表1 全风化花岗岩物理力学参数 Tab. 1 Physical properties of completely-strongly weathered granite |
 |
1.2 试验设计方法
因受风化程度等因素影响,同一区域全风化花岗岩含水率、黏土含量存在较大差异。根据响应面法分析注浆压力、全风化花岗岩地层初始含水率、黏土含量3个因素与土体抗崩解特性及抗压强度的作用关系,提出该地层注浆加固参数设计方法。
响应面法(response surface methodology,RSM)是一种综合试验设计和数学建模的优化方法[15-16],通过对具有代表性的局部各点进行试验,回归拟合全局范围内因素与结果间的函数关系,并且取得各因素最优水平值。根据现场取样测试所得参数,土体密度设计为1.97 g/cm3;初始含水率水平设计值为8%、14%、20%;黏土含量水平设计值为12%、20%、28%(将粒径小于0.075 mm的土样定义为黏性土颗粒,大于0.075 mm的土样定义为砂土)。
1.3 试验流程将现场原状土破碎、烘干,土样过0.075 mm分级筛,按照设计的地质参数重塑土样;注浆试验选用水灰比为1∶1的水泥单液浆,注浆压力为0.5、1.0、1.5 MPa。虽然原状土具有分级特性和分带特性,但本文旨在通过对注浆前后土体抗崩解特性及抗压强度的影响因素分析,建立全风化花岗岩地层注浆参数设计方法,进而指导注浆治理工程,因此存在的差异忽略不计。试验设计参数如表2所示。
| 表2 试验设计 Tab. 2 Test design |
 |
1.4 注浆模拟试验
基于山东大学自主研发的3维注浆模拟试验系统[17-18]开展注浆试验,试验主体装置如图1所示。
 |
| 图1 试验主体装置示意图 Fig. 1 Schematic view of grouting test system |
注浆后对加固土体的压密区进行取样[4],取样方式如图2所示,取样照片如图3所示。测试其抗崩解特性、抗压强度。
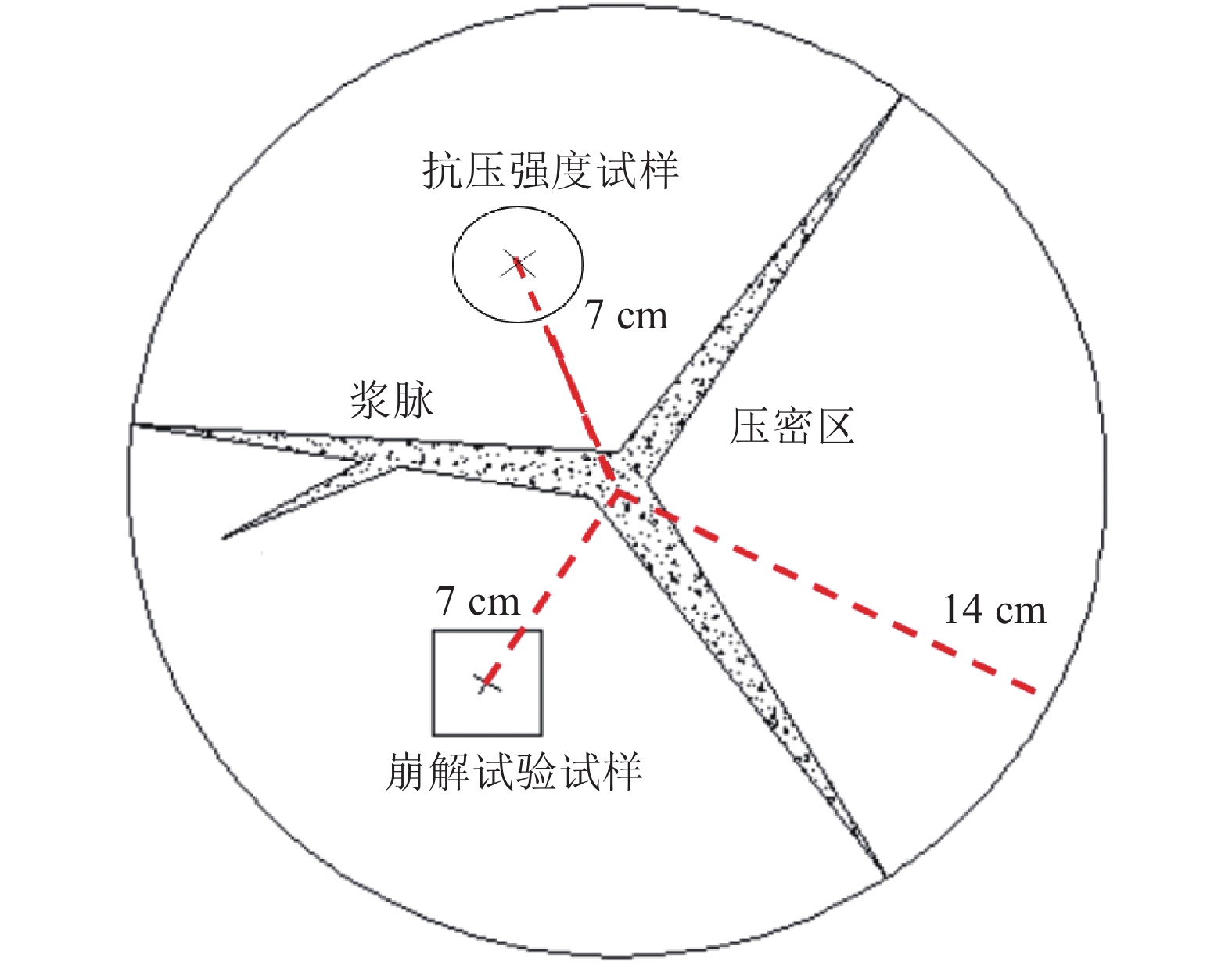 |
| 图2 取样示意图 Fig. 2 Sampling schematic diagram |
 |
| 图3 注浆后取样照片 Fig. 3 Soil sample after grouting |
崩解试验、无侧限单轴压缩试验按土工试验规程[19]进行,崩解试验每5 s读数一次,其中崩解试验中当浮筒刻度读数相隔10 min不变时停止试验,试验过程见图4。无侧限抗压强度试验采用长春市朝阳试验仪器有限公司制造的GAW–1000的微机控制电液伺服岩石刚性试验机,在无侧向压力条件下,采用位移作为加载控制方式,加载速度为1 mm/min。
 |
| 图4 崩解试验过程 Fig. 4 Disintegration test process |
2 结果与讨论 2.1 试验流程
响应面法的基本思想是通过一系列确定性试验,用多项式函数来近似隐式极限状态函数,本质上为一套统计方法[15-16]。运用响应面法设计的试验共17组(为保证试验准确性,5号试验重复5组),试验结果如表3所示。利用Design–Expert软件对表3中的试验结果进行回归拟合,即得到全风化花岗岩土样崩解时间的响应面函数,见式(1)~(2)。
| 表3 试验结果 Tab. 3 Test results |
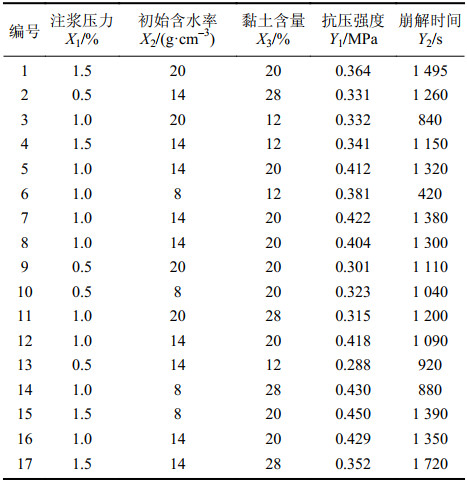 |
| $ \begin{aligned}[b] {Y_1} =& - 0.334\;69 - 0.208\;08{X_1} + 0.042\;6{X_2} + 0.039\;6{X_3} + \\ & 0.000\;4{X_1}{X_2} \!+\! 0.001\;2{X_1}{X_3}\! +\! 0.000\;2{X_2}{X_3} \!\!+\! 0.124{X_1^2}\! - \\ & 0.001\;6{X_2^2} - 0.000\;9{X_3^2} \end{aligned}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! $ | (1) |
| $ \begin{aligned}[b] {Y_2} =& - 1\;544.03 - 1\;565.08{X_1} + 204.19{X_2} + 160.33{X_3} + \\ & 2.92{X_1}{X_2} + 14.38{X_1}{X_3} + 0.52{X_2}{X_3} + 796.5 {X_1^2} -\\ & 6.34{X_2^2 }- 3.51{X_3^2} \end{aligned}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! $ | (2) |
对上述回归模型进行方差分析,结果见表4、5。注浆后全风化花岗岩试样抗崩解特性及抗压强度所选用的二次回归模型效果均非常显著(P均小于0.05)。
| 表4 抗压强度回归模型方差分析 Tab. 4 Analysis of variance with the regression model of compressive strength |
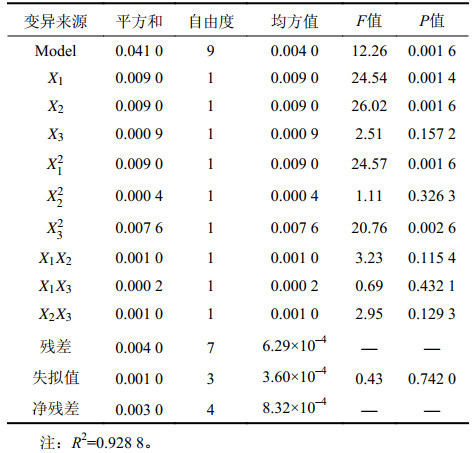 |
| 表5 崩解特性回归模型方差分析 Tab. 5 Analysis of variance with the regression model of disintegration time |
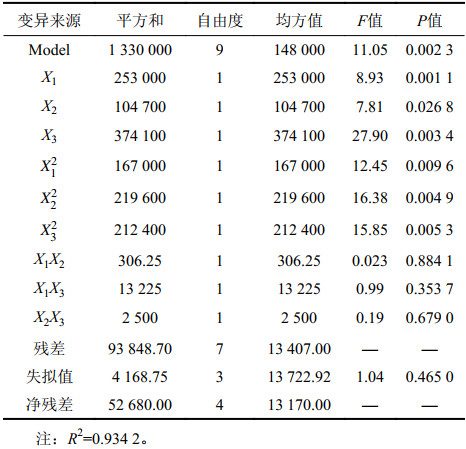 |
其中,拟合度分别为0.928 8、0.934 2,P值的失拟值分别为0.742和0.465(不显著),这说明注浆后全风化花岗岩试样抗崩解特性及抗压强度预测值与实测值之间具有良好的拟合优度,可用于注浆后全风化花岗岩加固效果的分析及预测,模型预测结果与样本数据的比较如图5、6所示。
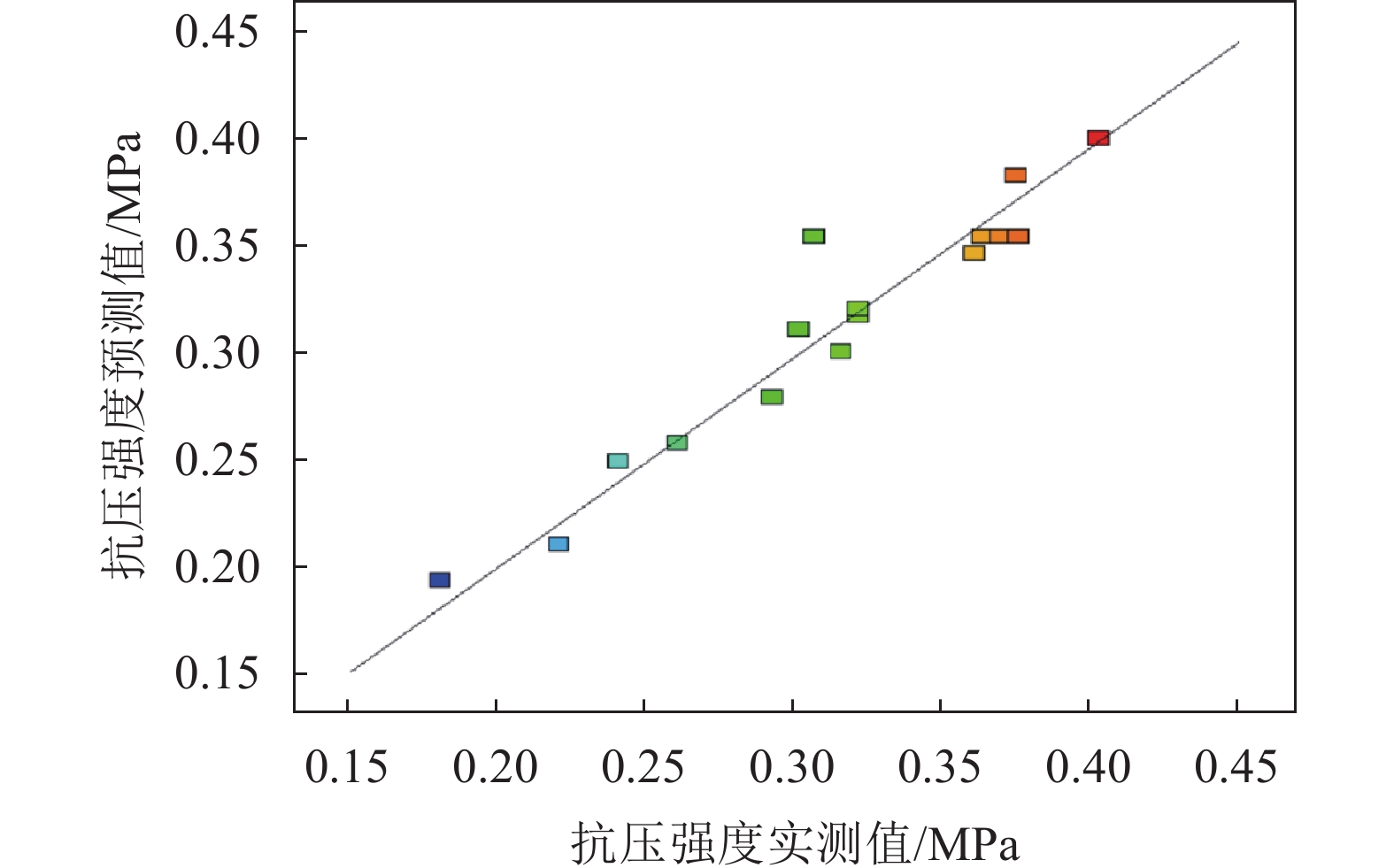 |
| 图5 抗压强度预测结果与样本数据的比较 Fig. 5 Comparison the predicted values of compressive strength with the test ones |
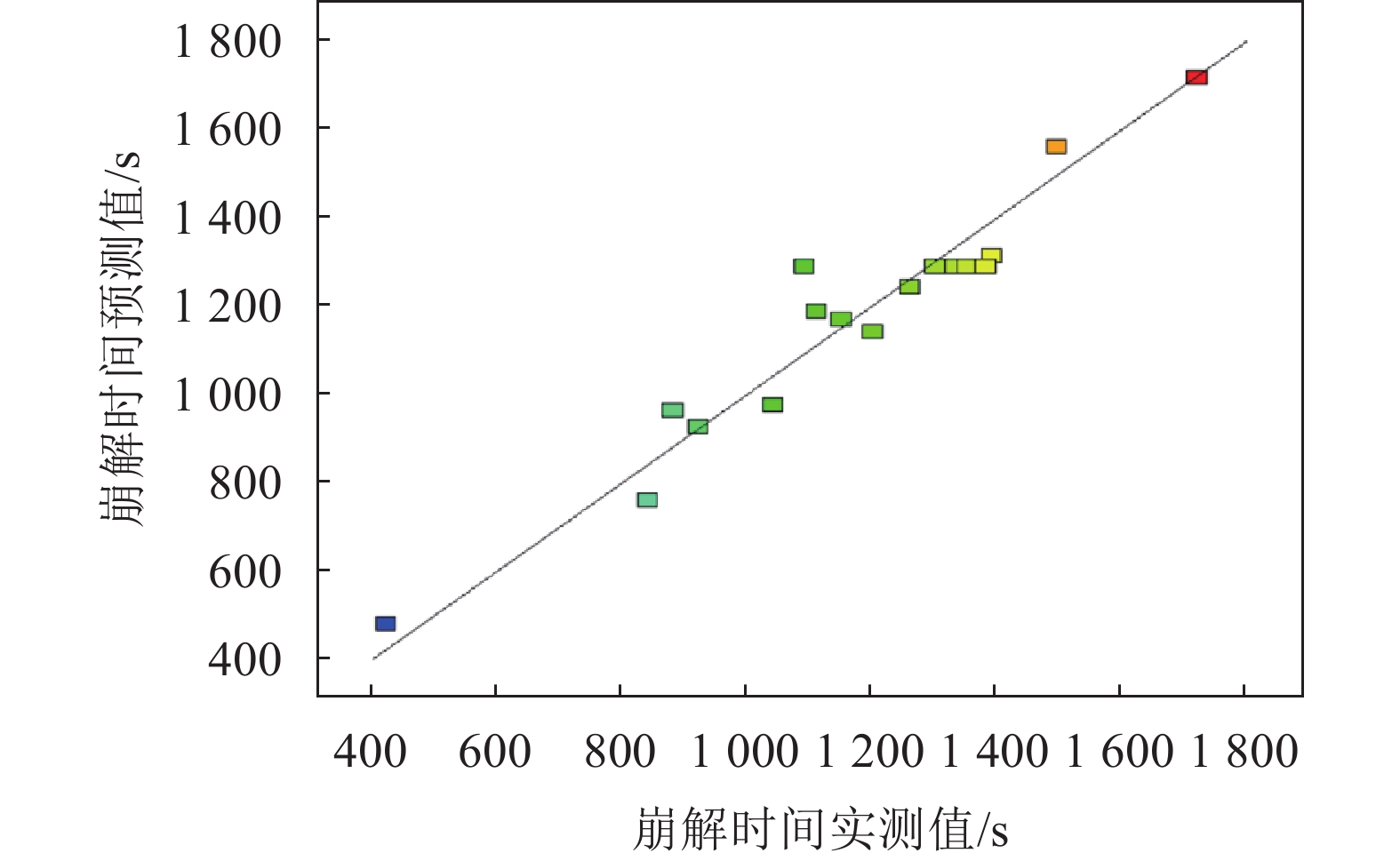 |
| 图6 崩解时间预测结果与样本数据的比较 Fig. 6 Comparison the predicted values of disintegration time with the test ones |
由表4可知,X1、X2的P值(显著性分析)均小于0.05,即注浆压力和初始含水率对全风化花岗岩的抗压强度具有显著影响。由P值分析可知,3种因素对注浆后全风化花岗岩抗压强度影响作用的大小顺序为注浆压力>初始含水率>黏土含量。
由表5可知,X1、X2、X3的P值(显著性分析)均小于0.05,即注浆压力、初始含水率和黏土含量对全风化花岗岩的崩解特性具有显著影响。由P值分析可知,3种因素对注浆后全风化花岗岩崩解特性影响作用的大小顺序为注浆压力>黏土含量>初始含水率。
2.2 响应面参数对注浆加固效果的影响 2.2.1 响应面参数对全风化花岗岩抗压强度的影响不同条件下全风化花岗岩抗压强度拟合曲线如图7所示。
 |
| 图7 抗压强度拟合曲线 Fig. 7 Fitting curves of compressive strength |
由图7(a)可知,土体试样抗压强度都随注浆压力的增大显著提高。当注浆压力达到1.5 MPa后增长幅度逐渐平缓,这是由于在注浆压力较高条件下,更有利于浆脉的扩展,浆脉厚度不断增大,对周边土体的压密作用增强;当注浆压力达到1.5 MPa时,浆液压滤作用明显,主浆脉通道浆液浓度大幅提升,浆脉厚度扩展缓慢,对周边土体的压密作用削弱,因此土体抗压强度增长缓慢。
由图7(b)可知,全风化花岗岩土体初始含水率与注浆后土体抗压强度呈抛物线关系。劈裂注浆过程中,加固效果一定程度上取决于土体的可压缩性。对于砂土地层的可压缩性存在最优含水率[20]。试验中,当初始含水率小于16%时,土体的可压缩性与初始含水率成正比,有利于浆脉的扩展,土体抗压强度增长幅度大;当初始含水率达到16%后,土体可压缩性逐渐降低,浆脉厚度逐渐减小,土体抗压强度开始下降。
如图7(c)所示,全风化花岗岩试样的抗压强度与黏土含量呈抛物线关系。当全风化花岗岩黏土含量低时,土体可压缩性主要由砂颗粒组成的砂骨架控制,黏土含量升高时,土体可压缩性呈上升趋势。因此,黏土含量升高,土体中形成的浆脉宽度增加,挤密作用增强,注浆后土体抗压强度增加。但当黏土含量超过24%时,因土体抗拉强度小,水泥浆液更倾向于沿着劈裂通道向前方运移,形成的浆脉宽度减小,注浆后土体抗压强度逐渐降低。
2.2.2 响应面参数对全风化花岗岩崩解特性的影响全风化花岗岩不同条件下的崩解时间曲线如图8所示。
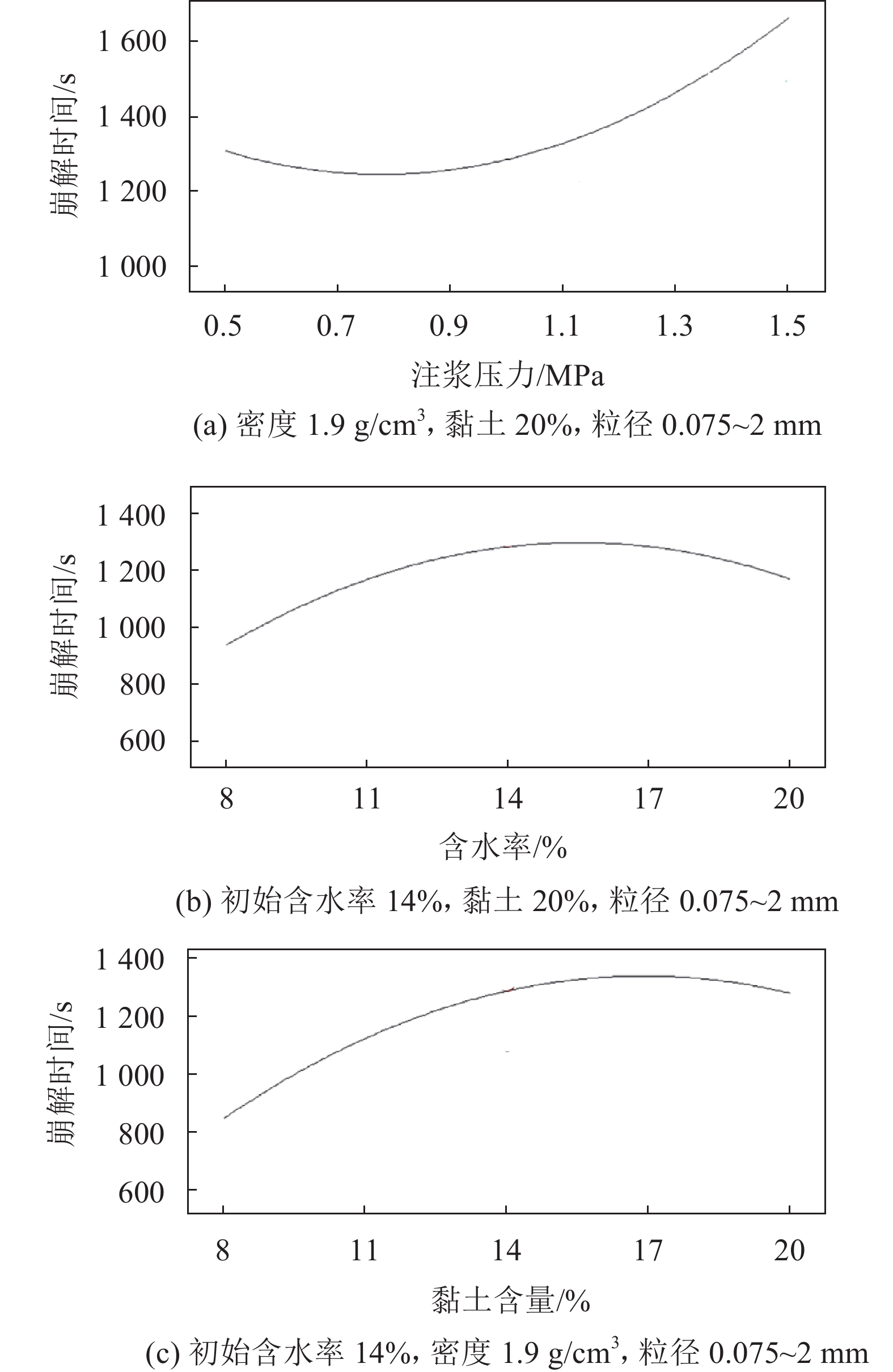 |
| 图8 崩解时间拟合曲线 Fig. 8 Fitting curves of disintegration time |
由图8(a)可知,试验参数范围内试样崩解时间与注浆压力成正相关,崩解时间变化范围为1 200~1 650 s。水泥浆液在全风化花岗岩地层中以挤密方式加固土体,注浆压力一定程度上决定了全风化花岗岩的孔隙性、透水性和胶结状态。注浆压力升高,土体的胶结能力提高,孔隙性和透水性降低,从而导致其遇水崩解时间延长。
由图8(b)可知,试验参数范围内试样崩解时间随含水率的增加呈现先升高后降低的趋势,崩解时间变化范围为930~1 250 s,初始含水率为14%~17%时崩解时间最长。全风化花岗岩中初始含水率影响土颗粒之间相互接触关系及土体中黏土矿物的膨胀性能,改变土体粒间吸力,进而影响全风化花岗岩的崩解特性。初始含水率升高,全风化花岗岩试样中的黏土颗粒已发生膨胀,遇水后其膨胀性减低,导致崩解时间升高;当初始含水率高于17%时,初始含水率的增大使土颗粒间的接触距离增大,导致土颗粒间存在的吸力降低,土颗粒间的润滑程度增大,易于滑动,导致崩解时间降低。
由图8(c)可知,试样崩解时间随黏土含量的升高呈现先升高后降低的趋势,崩解时间变化范围为820~1 360 s。黏土在全风化花岗岩中具有胶结作用,当黏土含量低于25%时,全风化花岗岩遇水后黏土膨胀力不足以破坏土体,因此崩解时间与黏土含量成正比;当黏土含量高于25%时,水与土体中的黏土发生反应,产生膨胀作用,在细微裂缝处产生应力集中,形成尖劈作用,产生裂缝并破坏土体,加速土体的崩解。
3 注浆参数设计方法全风化花岗岩地层地质参数复杂多变,注浆加固治理工程中的注浆参数设计缺乏可靠判据。本文依据响应面法模拟试验结果,分析注浆压力、初始含水率、黏土含量对注浆后土体抗崩解特性及抗压强度的交互作用,提出全–强风化花岗岩地层注浆参数设计方法,以期指导实际注浆工程。
3.1 基于抗压强度的注浆参数设计基于表4,注浆压力和土体初始含水率对注浆后土体抗压强度影响显著,黏土含量为20%时,二者对抗压强度的交互作用如图9所示。
 |
| 图9 抗压强度交互作用曲线 Fig. 9 Interaction curves of compressive strength |
由图9可知,当黏土含量为20%时,初始含水率可分为低压注浆区(0.5~1.0 MPa)和高压注浆区(1.0~1.5 MPa)。在低压注浆区内,注浆后土体抗压强度均高于0.35 MPa,综合考虑注浆成本及围岩稳定性差,当初始含水率为12%~17%时,注浆压力可设计为0.5~1.0 MPa。在高压注浆区,当注浆压力小于1 MPa时,注浆后土体力学强度较小(小于0.35 MPa);当注浆压力超过1 MPa时,注浆后土体力学强度显著升高,因注浆压力超过1.5 MPa时,土体抗压强度增长变缓(图7(a)),高压注浆区注浆压力设计为1.0~1.5 MPa,最高注浆压力可根据实际注浆工程需求,在考虑围岩稳定性条件下适当升高。
3.2 基于抗崩解特性的注浆参数设计由表5可知,注浆压力、土体初始含水率及黏土含量均对土体抗崩解特性影响显著。黏土含量为20%时,注浆压力与初始含水率对抗崩解特性的交互作用如图10(a)所示;初始含水率为14%时,注浆压力与黏土含量对抗崩解特性的交互作用如图10(b)所示。
 |
| 图10 崩解时间交互作用曲线 Fig. 10 Interaction curves of disintegration time |
由图10可知,依据注浆后土体的抗崩解特性,初始含水率和黏土含量可分为低压注浆区(0.5~1.0 MPa)、高压注浆区(1.0~3.0 MPa)。
图10(a)中,在低压注浆区内,注浆后土体崩解时间均高于1 300 s,当初始含水率为12%~17%时,注浆压力可设计为0.5~1.0 MPa。高压注浆区压力小于1.0 MPa时,注浆后土体抗崩解特性较差(小于1 200 s)。当注浆压力超过1.0 MPa时,注浆后土体力学强度显著升高,综合考虑注浆成本及围岩稳定性,高压注浆区注浆压力设计值为1.0~3.0 MPa。
图10(b)中,在低压注浆区内,注浆后土体崩解时间均高于1 300 s,当黏土含量为19%~25%时,注浆压力可设计为0.5~1.0 MPa。当高压注浆区压力小于1.0 MPa时,注浆后土体抗崩解特性较差(小于1 200 s),压力超过1.0 MPa时,注浆后土体力学强度显著升高,综合考虑注浆成本及围岩稳定性,高压注浆区注浆压力设计值为1.0~3.0 MPa。
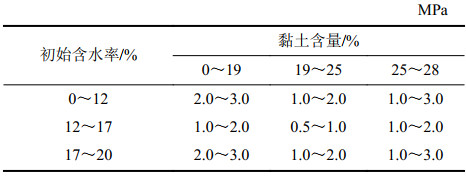
综上所述,基于注浆后土体的抗崩解特性和抗压强度,可依据土体初始含水率及黏土含量指导注浆参数设计(表6),当二者对注浆参数设计不一致时采用中压注浆(1.0~2.0 MPa)。
| 表6 基于抗崩解特性的注浆参数设计 Tab. 6 Grouting parameters design based on anti-disintegration characteristics |
 |
4 现场试验 4.1 方案设计
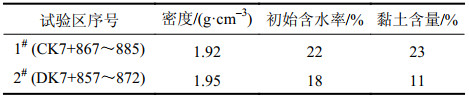
广西均昌隧道建设过程中需穿越全–强风化花岗岩地层,为确保隧道安全开挖,拟采用帷幕注浆法对其实施系统加固。以进口左洞CK7+867~885及进口右洞DK7+852~867里程段为例,开展现场工程试验,两区段地质参数如表7所示。因两处土体初始含水率均位于高压注浆区,以黏土含量为依据设计注浆压力。注浆材料选用水灰比为1∶1的水泥单液浆,注浆压力设计值分别为0.5 MPa(低压)和2.0 MPa(高压)。
| 表7 全风化花岗岩物理力学参数 Tab. 7 Physical properties parameters of completely weathered granite |
 |
依据试验研究结果,1#、2#试验区注浆参数设计如图11所示。其中,红色为高压注浆区,蓝色为低压注浆区。
 |
| 图11 注浆参数设计 Fig. 11 Design of grouting parameters |
4.2 注浆加固效果分析
帷幕注浆完成后,隧道开挖断面如图12所示,采用钻孔方式于压密区取样,测试注浆后土体的抗崩解特性和抗压强度,试验结果如图13~14所示。
 |
| 图12 不同加固区劈裂浆脉 Fig. 12 Grouting veins of different grouted zone |
 |
| 图13 注浆后土体抗压强度 Fig. 13 Compressive strength after grouting |
 |
| 图14 注浆后土体抗崩解特性 Fig. 14 Disintegration characteristics after grouting |
由图13可知,因初始含水率对注浆后土体抗压强度影响显著,当注浆压力上升时,土体抗压强度显著增大。由图14可知:在低压注浆区,增大注浆压力对于土体抗崩解特性影响较小;在高压注浆区,注浆压力提升对土体抗崩解特性具有显著效果。现场试验结果与试验结论相吻合,验证了研究结果的可靠性。
5 结 论基于响应面法,通过室内注浆模拟试验分析了注浆压力、全–强风化花岗岩初始含水率及黏土含量3个因素对注浆后土体抗压强度及崩解特性的作用规律,并提出该地层注浆参数设计判据,研究结果将为该地层注浆工程中注浆参数设计及注浆加固效果评判提供一定指导意义。获得结论如下:
1)注浆压力对注浆后土体抗崩解特性和抗压强度具有显著影响。注浆压力的升高,土体抗压强度显著增加,当注浆压力达到1.5 MPa时,增幅区域平缓;注浆压力与土体抗崩解特性成正相关关系。
2)初始含水率对注浆后土体抗崩解特性和抗压强度影响大,且随着初始含水率的升高,二者均呈先升高后降低的趋势。
3)黏土含量对注浆后土体抗压强度影响较小,但对土体抗崩解特性具有显著影响,随着黏土含量的增加,土体抗崩解特性呈现先升高后降低的趋势。
4)基于响应面法分析结果,注浆压力、初始含水率、黏土含量对注浆后土体抗崩解特性影响程度大小顺序为注浆压力>初始含水率>黏土含量,对抗压强度影响程度的顺序为注浆压力>黏土含量>初始含水率。依据各因素间的交互作用,注浆压力设计值可基于初始含水率和黏土含量分为低压注浆区(0.5~1.0 MPa)、中压注浆区(1.0~2.0 MPa)和高压注浆区(2.0~3.0 MPa),研究成果可指导该地层注浆加固治理参数设计。
5)通过现场试验验证了本文结论的可靠性及适用性,研究成果将为全风化花岗岩及相似地层的注浆加固治理提供一定指导作用。
| [1] |
Hong Dawei,Wang Tao,Tong Ying.An outline about granitoids in China[J].2007,53(Suppl):9–16. 洪大卫,王涛,童英.中国花岗岩概述[J].地质评论,2007,53(增刊):9–16. |
| [2] |
Zhao Jianjun,Wang Sijing,Shang Yanjun,et al. Control factors on shear strength of completely decomposed granite[J]. Rock and Soil Mechanics, 2005, 26(4): 624-628. [赵建军,王思敬,尚彦军,等. 全–强风化花岗岩抗剪强度影响因素分析[J]. 岩石力学, 2005, 26(4): 624-628. DOI:10.16285/j.rsm.2005.04.025] |
| [3] |
Yuan Jingqiang,Chen Weizhong,Huang Shiwu,et al. Experimental study on physico-mechanical properties of grouted completely weathered granite[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(增1): 2876-2882. [袁敬强,陈卫忠,黄世武,等. 全–强风化花岗岩注浆加固特性试验研究[J]. 岩石力学与工程学报, 2016, 35(增1): 2876-2882. DOI:10.13722/j.cnki.jrme.2015.0378] |
| [4] |
Wang Kai,Li Shucai,Yang Lei,et al. Grouting simulation experiment on reinforcement characteristics of completely decomposed granite[J]. Journal of Tianjin University (Science and Technology), 2017, 50(11): 1199-1209. [王凯,李术才,杨磊,等. 全–强风化花岗岩加固特性注浆模拟试验[J]. 天津大学学报(自然科学与工程技术版), 2017, 50(11): 1199-1209. DOI:10.11784/tdxbz201702057] |
| [5] |
Zhang Shu,Tang Huiming. Experimental study of disintegration mechanism for unsaturated granite residual soil[J]. Rock and Soil Mechanics, 2013, 34(6): 1668-1676. [张抒,唐辉明. 非饱和花岗岩残积土崩解机制试验研究[J]. 岩土力学, 2013, 34(6): 1668-1676. DOI:10.16285/j.rsm.2013.06.009] |
| [6] |
Li Jianxin,Chen Qiunan,Zhao Liu,et al. Experimental research on disintegration characteristics of weathered granite in Nanyue[J]. Journal of Hunan University of Science & Technology(Natural Science Edition), 2015, 30(4): 59-63. [李建新,陈秋南,赵柳,等. 南岳地区全–强风化花岗岩崩解特性试验研究[J]. 湖南科技大学学报(自然科学版), 2015, 30(4): 59-63. DOI:10.13582/j.cnki.1672-9102.2015.04.010] |
| [7] |
Tan Jianyi. Study on disintegration mechanism of solum in covering karst zones in Guangxi province[J]. Journal of Engineering Geology, 2001, 9(3): 273-277. [谭鉴益. 广西覆盖型岩溶区土层崩解机理研究[J]. 地质工程学报, 2001, 9(3): 273-277.] |
| [8] |
Yang Mijia,Chen Mingxiong,He Yongnian. Current research state of grouting technology and its development direction infuture[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(6): 839-841. [杨米加,陈明雄,贺永年. 注浆理论的研究现状及发展方向[J]. 岩石力学与工程学报, 2001, 20(6): 839-841. DOI:10.3321/j.issn:1000-6915.2001.06.019] |
| [9] |
Zhang Jian,Li Shucai,Li Zhaofeng,et al. Comparative study of reinforcement patterns between single- and double- fluid grouting in fully-weathered granite[J]. Journal of Central South University (Science and Technology), 2018, 49(12): 3051-3059. [张健,李术才,李召峰,等. 全风化花岗岩地层单–双液浆加固试验研究[J]. 中南大学学报(自然科学版), 2018, 49(12): 3051-3059. DOI:10.11817/j.issn.1672-7207.2018.12.019] |
| [10] |
Cui Hongqin. Construction technology of ultra shallow water rich fully weathered granite and large section tunnel[J]. Railway Construction Technolgy, 2014(3): 1-5. [崔红琴. 超浅埋富水全–强风化花岗岩大断面隧道施工技术[J]. 铁道建筑技术, 2014(3): 1-5. DOI:10.3969/j.issn.1009-4539.2014.03.001] |
| [11] |
Guo Xiaohong,Wang Mengshu. Study on the grouting technology adopted in F1 weathered trough for Xiamen Xiang’an subsea tunnel[J]. Chinese Engineering Science, 2011, 13(9): 38-41. [郭小红,王梦恕. 厦门翔安海底隧道F1风化深槽注浆加固技术[J]. 中国工程科学, 2011, 13(9): 38-41. DOI:10.3969/j.issn.1009-1742.2011.09.005] |
| [12] |
Li Rong,Li Zhiguo. Study on the grouting technology adopted in strong- weathered granite for an under-sea tunnel[J]. Modern Tunnelling Technology, 2008, 45(1): 21-29. [李蓉,李治国. 海底隧道全强风化花岗岩地层注浆技术研究[J]. 现代隧道技术, 2008, 45(1): 21-29. DOI:10.13807/j.cnki.mtt.2008.01.008] |
| [13] |
Zhang Dingli,Sun Feng,Li Pengfei. Mechanism of composite grouting subsea tunnel and its application[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(3): 445-452. [张顶立,孙锋,李鹏飞. 海底隧道复合注浆机制研究及工程应用[J]. 岩石力学与工程学报, 2012, 31(3): 445-452. DOI:10.3969/j.issn.1000-6915.2012.03.002] |
| [14] |
Li Xianghui,Zhang Qingsong,Zhang Xiao,et al. Grouting diffusion mechanism in heterogeneous fault-fracture zone[J]. Advanced Engineering Sciences, 2018, 50(2): 67-76. [李相辉,张庆松,张霄,等. 非均质断层破碎带注浆扩散机理[J]. 工程科学与技术, 2018, 50(2): 67-76. DOI:10.15961/j.jsuese.201700413] |
| [15] |
Chen Bing,Liao Guangming,Zhao Lei. Seismic reliability analysis of the basket-handle arch based on the response surface method[J]. Advanced Engineering Science, 2008, 40(2): 44-48. [陈兵,廖光明,赵雷. 基于响应面法的复式钢箱提篮拱地震可靠度分析[J]. 工程科学与技术, 2008, 40(2): 44-48. DOI:10.15961/j.jsuese.2008.02.013] |
| [16] |
Jiang Shuihua,Qi Xiaohui,Cao Zijun,et al. System reliability analysis of slope with stochastic response surface method[J]. Rock and Soil Mechanics, 2015, 36(3): 809-819. [蒋水华,祁小辉,曹子君,等. 基于随机响应面法的边坡系统可靠度分析[J]. 岩土力学, 2015, 36(3): 809-819. DOI:10.16285/j.rsm.2015.03.027] |
| [17] |
Li Zhaofeng,Li Shucai,Zhang Qingsong,et al. Model tests on grouting reinforcement of water-rich broken rock mass[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(12): 2246-2253. [李召峰,李术才,张庆松,等. 富水破碎岩体注浆加固模拟试验及应用研究[J]. 岩土工程学报, 2016, 38(12): 2246-2253. DOI:10.11779/CJGE201612013] |
| [18] |
Li Peng,Zhang Qingsong,Zhang Xiao,et al. Comparison research on reinforcement characteristics of cement slurry and C–S slurry for inhomogeneous fault medium[J]. Journal of Basic Science and Engineering, 2016, 24(4): 840-852. [李鹏,张庆松,张霄,等. 非均质断层介质单双液加固特性对比[J]. 应用基础与工程科学学报, 2016, 24(4): 840-852. DOI:10.16058/j.issn.1005-0930.2016.04.019] |
| [19] |
南京水利科学研究院.土工试验规程:SL237—1999[S].北京:中国水利水电出版社,1999.
|
| [20] |
Zhang Lianzhen.Study on penetration and reinforcement mechanism of grouting in sand layer disclosed by subway tunnel and its application[D].Jinan:Shandong University,2017. 张连震.地铁穿越砂层注浆扩散与加固机理及工程应用[D].济南:山东大学,2017. |
 2019, Vol. 51
2019, Vol. 51


