2. 中国地质大学(北京) 工程技术学院,北京 100083
2. School of Eng. and Technol., China Univ. of Geosciences (Beijing), Beijing 100083, China
堰塞湖是在一定的地质与地貌条件下,由于地震、滑坡、泥石流等因素引发的自然堆积体横向阻塞河谷后,造成上游段壅水而形成的湖泊[1]。在中国青藏高原的高山峡谷区,不仅易形成滑坡堰塞湖,还有可能形成破坏力巨大的溃坝洪水[2],如易贡堰塞湖[3]、白格堰塞湖[4]等。堰塞体的溃决模式主要有漫顶溢流、渗透破坏和坝坡失稳3种[5],堰塞体自身结构特征与组成材料的物理力学性质是影响溃决模式的主要因素之一。堰塞体形成之后,及时分析其组成材料的物理力学性质,对于堰塞体安全评估、溃决模式分析等均有着较为重要的意义。
目前,确定堰塞体物理力学性质的研究手段主要有原位试验、室内试验与数值模拟3种[6]。如Chang等[7]通过原位试验测试了堰塞体的侵蚀性,Okeke[8]、刘汉东[9]、柴贺军[10]和Ma[11]等分别通过三轴压缩等室内试验研究了舟曲、扣山等堰塞体的临界水力比降、强度等力学参数。原位试验和室内试验对于观察堰塞体的力学性质起到重要作用,但受到试样尺寸、试验设备等试验条件的限制,较难反映堰塞体的实际力学性质。数值模拟试验凭借其可重复性、便利性、尺寸限制少等特点,可作为原位试验和室内试验的一种重要补充研究手段[6]。杨江涛等[12]采用离散元法,模拟了堰塞体材料的直剪试验,从宏观和微观的角度对堰塞体的力学特性进行了研究,指出基于离散元的数值模拟试验可以较好的克服室内试验的问题,直接获取试验内部接触力的分布与传递情况,从而优化堰塞体力学特性的研究。
堰塞体的物理力学特性研究需考虑相应的应力状态和应力路径[6]。在堰塞湖水位壅高过程中,堰塞体应力路径为常剪应力,即剪应力保持不变,孔隙水压力不断增加,平均有效应力不断降低。国内外主要研究了砂土材料在常剪应力路径下的力学特性[13-15],对于堰塞体往往开展的是三轴固结排水剪或固结不排水剪试验[9,11],这与堰塞湖水位壅高过程中的实际应力路径有别。因此开展常剪应力路径下堰塞体材料的变形特性研究,是深入分析湖水位壅高过程中堰塞体动态响应的有效途径。
2018年10月11日,西藏自治区江达县波罗乡白格村与四川省白玉县绒盖乡则巴村交界处金沙江右岸发生高位山体滑坡,堵塞金沙江,形成堰塞湖。堰塞体最高处高出江面60 m,平均高出江面40 m,堰塞湖水位最高为36.4 m[16]。10月12日,堰塞体发生漫顶破坏,堰塞湖水开始自然下泄。
本文以白格堰塞体为例,建立了土料离散元(DEM)模型,利用孔隙有限体积法(PFV)建立了孔隙尺度的流体网格,通过DEM–PFV耦合数值模拟开展了堰塞体材料常剪应力路径三轴试验,从数值模拟敏感性分析的角度研究了湖水位壅高过程中的土料变形特性,为分析堰塞体在湖水位壅高条件下的动态响应提供有益帮助。
1 DEM–PFV–流固耦合模拟 1.1 离散元(DEM)原理离散元法将颗粒材料视为具有一定大小、密度和刚度的球形颗粒,且颗粒运动规律遵循牛顿第二定律[17]:
| ${{{F}}_i} = {m_i}{{{a}}_i}$ | (1) |
其中,mi为颗粒i的质量,ai为颗粒加速度,Fi为颗粒牵引力。
相邻颗粒间法向力根据颗粒重叠的距离来确定[18]:
| ${{{F}}_{{\rm{n}},ij}} = {k_{{\rm{n}},}}_{ij}\Delta {D_{ij}} \cdot {{{n}}_{{\rm{n}},ij}}$ | (2) |
其中,Fn,ij为颗粒间法向力,kn,ij为法向刚度,ΔDij为颗粒间重叠距离,nn,ij为颗粒间相互作用力的单位矢量。
颗粒间剪切应力根据切向位移确定[18]:
| $\Delta {{{F}}_{{\rm{s}},ij}} = {k_{{\rm{s}},}}_{ij}\Delta {u_{{\rm{s}},}}_{ij} \cdot {{{n}}_{{\rm{s}},ij}}$ | (3) |
| ${{F}}_{{\rm{s}},ij}^t = {{F}}_{{\rm{s}},ij}^{t - \Delta t} + \Delta {{{F}}_{{\rm{s}},ij}}$ | (4) |
其中,
最终,颗粒的牵引力为[18]:
| ${{{F}}_i} = \sum\limits_{j = 1}^n {({{{F}}_{{\rm{n}},ij}} + {{{F}}_{{\rm{s}},ij}})} $ | (5) |
作者利用开源程序YADE[19]开展离散元模拟。
1.2 孔隙有限体积法(PFV)在孔隙有限体积法(pore finite volume,PFV)中,离散元颗粒被Delaunay三角剖分为四面体网格,四面体网格的顶点为离散元颗粒,一个四面体网格代表一个孔隙。全部的四面体网格构成孔隙网络,用于建立斯托克斯流[20-22]。连续方程为:
| ${\dot V_{{\rm{p}},i}} = \int\limits_{\partial {\Theta _i}} {({{u}} - {{v}}) \cdot {{{{n}} {\rm{d}}}}S} $ | (6) |
其中,
| ${\dot V_{{\rm{p}},i}} = \sum\limits_{j = 1}^4 {\int\limits_{S_{ij}^f} {\left( {{{u}} - {{v}}} \right) \cdot {{n}}{\rm{ d}}S} } = \sum\limits_{j = 1}^4 {{q_{ij}}} $ | (7) |
局部压力梯度:
| ${q_{ij}} = {k_{ij}}\frac{{{p_i} - {p_j}}}{{{l_{ij}}}}$ | (8) |
其中,pi和pj为相邻孔隙的压力,lij为连接相邻孔隙的通道长度,导水率gij=kij/lij。在t时刻:
| $\sum\limits_{j = 1}^4 {{g_{ij}}} \left( {p_i^{\left[ {t + \Delta t} \right]} - p_j^{\left[ {t + \Delta t} \right]}} \right) = \dot V_{{\rm{p}},i}^{\left[ t \right]} + Q_i^{\left[ t \right]}$ | (9) |
其中,Qi为孔隙i的源项。
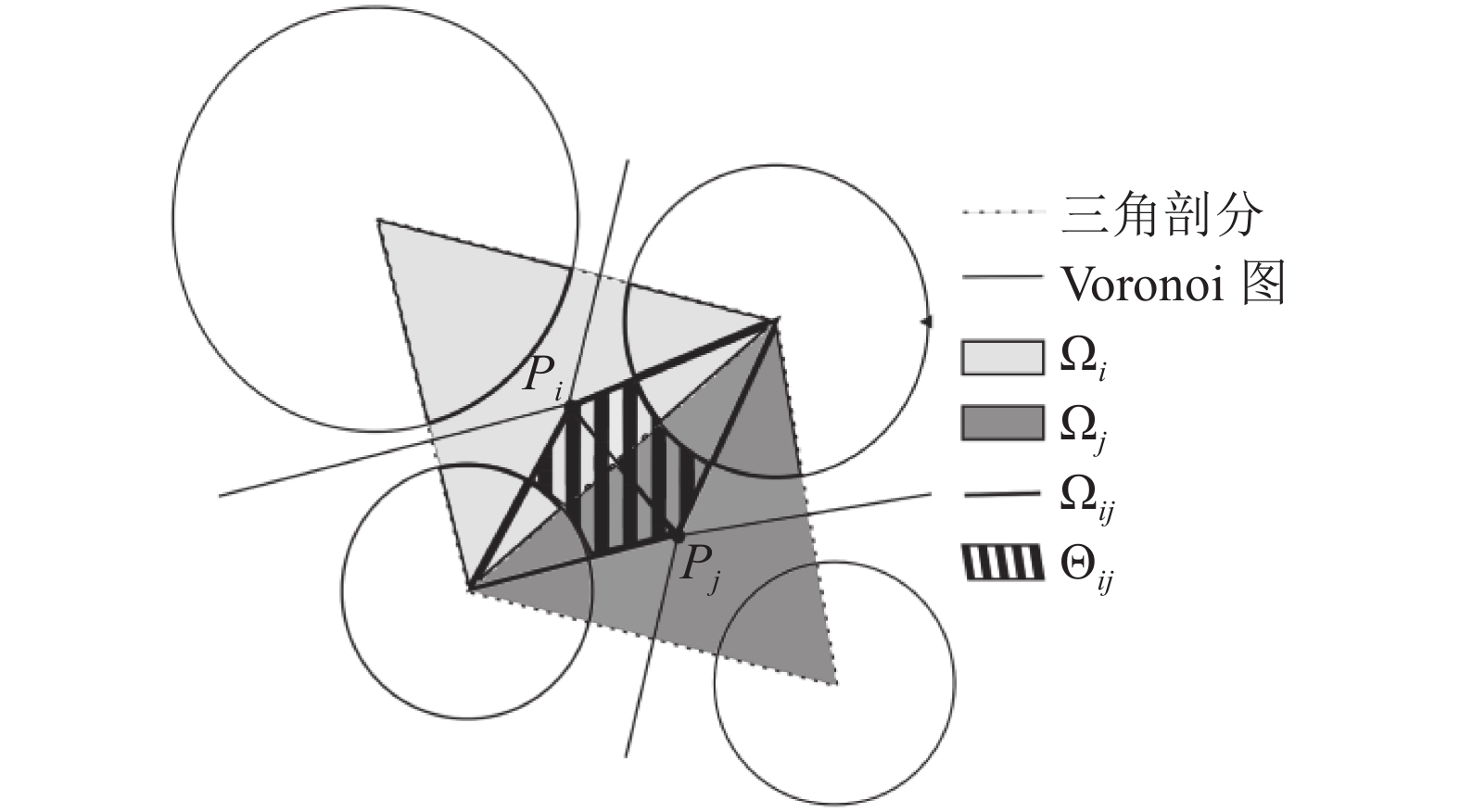
1.3 DEM–PFV耦合模拟方法DEM–PFV耦合方法[20-22]是处理流体与固体相互作用的一种耦合模型,如图1所示[22],在空间中,将离散元球体进行Delaunay三角剖分,形成由四面体网格构成的网络。Ωi为四面体网格i定义的域,其中包含了流体域Θi,相邻两个三角剖分产生的Voronoi单元交点Pi和Pj,以及固体颗粒所围成的域Θij,为两个孔隙网格交换流量的孔喉。
流体对固体颗粒的作用力Fk包括绝对压力p和黏性应力τ:
| ${{{F}}^{\rm{k}}} = \int\limits_{\partial {\Gamma _k}} {({p^*}{{{{n}} + }}\tau {{{{n}}}}){\rm{d}}S} $ | (10) |
其中,测压管压力
| ${{{F}}^{\rm{k}}} = {{{F}}^{{\rm{b}},{\rm{k}}}} + {{{F}}^{{\rm{p}},{\rm{k}}}} + {{{F}}^{{\rm{v}},{\rm{k}}}}$ | (11) |
其中,Fb,k为静水压力产生的浮力。流体流动产生的法向力Fp,k由下式计算:
| ${{F}}_{ij}^{{\rm{p}},{\rm{k}}} = {{A}}_{ij}^{\rm{k}}({p_i} - {p_j}){{{n}}_{ij}}$ | (12) |
其中,
黏性应力产生的切向力由下式计算:
| ${{F}}_{ij}^{{\rm{v}},{\rm{k}}} = \int\limits_{{\partial ^s}{\Theta _{ij}}} {\tau {{n}}{\rm{d}}S} $ | (13) |
一般的DEM–CFD耦合方法要求流体的网格要大于颗粒的粒径[23],而DEM–PFV耦合方法则不受其限制,实现了颗粒孔隙尺度的流体网格划分,并通过连续性方程和Navier–Stokes方程来较好地模拟颗粒与流体之间的相互作用。目前DEM–PFV耦合方法已经广泛用于土体内部侵蚀的研究[24-25]、饱和土沉降模拟研究[26]等,直观地揭示了土颗粒与孔隙水在微观尺度的相互作用。
2 模拟条件 2.1 初始条件本模拟中,初始条件的建立共分为数值建模、等压固结和偏压固结3个阶段。
1)数值建模
以白格堰塞体为例建立模型开展模拟。在实际建模过程中,为避免尺寸效应,模型的边长应不小于最大粒径的5倍。白格堰塞湖的实际颗粒级配较宽,且最大粒径超出最小粒径的1000倍,如果完全按照该级配来建模,会导致所建模型颗粒数量巨大,计算量超出计算机的性能,导致计算不能进行,所以离散元建模时通常对级配进行调整[27]。鉴于此,在白格堰塞体材料的离散元建模过程中,参照实际级配曲线,根据《土工试验方法标准》(GB/T 50123—2019)中的《粗颗粒土的试验制备》,采取剔除法进行了调整,模拟级配只选用了5 mm以下的粒径,如图2所示。
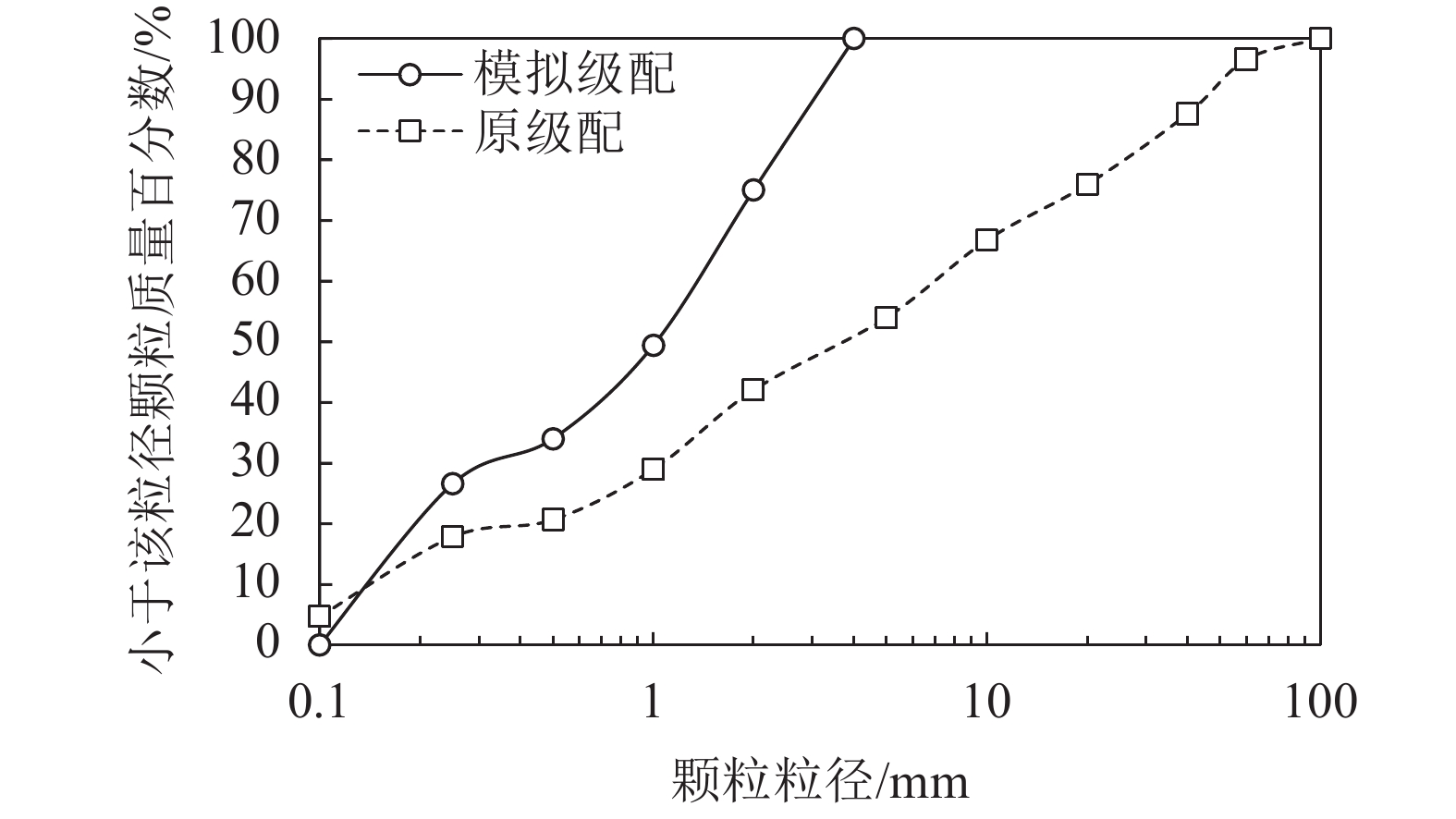 |
| 图2 模拟颗粒级配 Fig. 2 Particle size distribution |
在模型生成时,首先生成一个由六面相互正交的无摩擦刚性墙体围成的立方体。然后按照设定级配生成随机分布的颗粒,最终生成的颗粒数量为46600个。图3为模型图及边界条件,其中
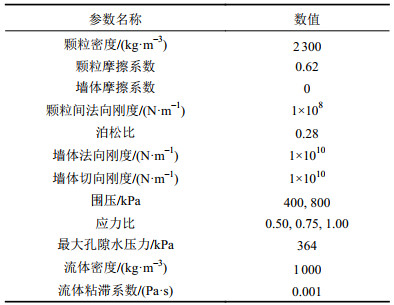
| 表1 模拟参数 Tab. 1 Parameters in simulation |
 |
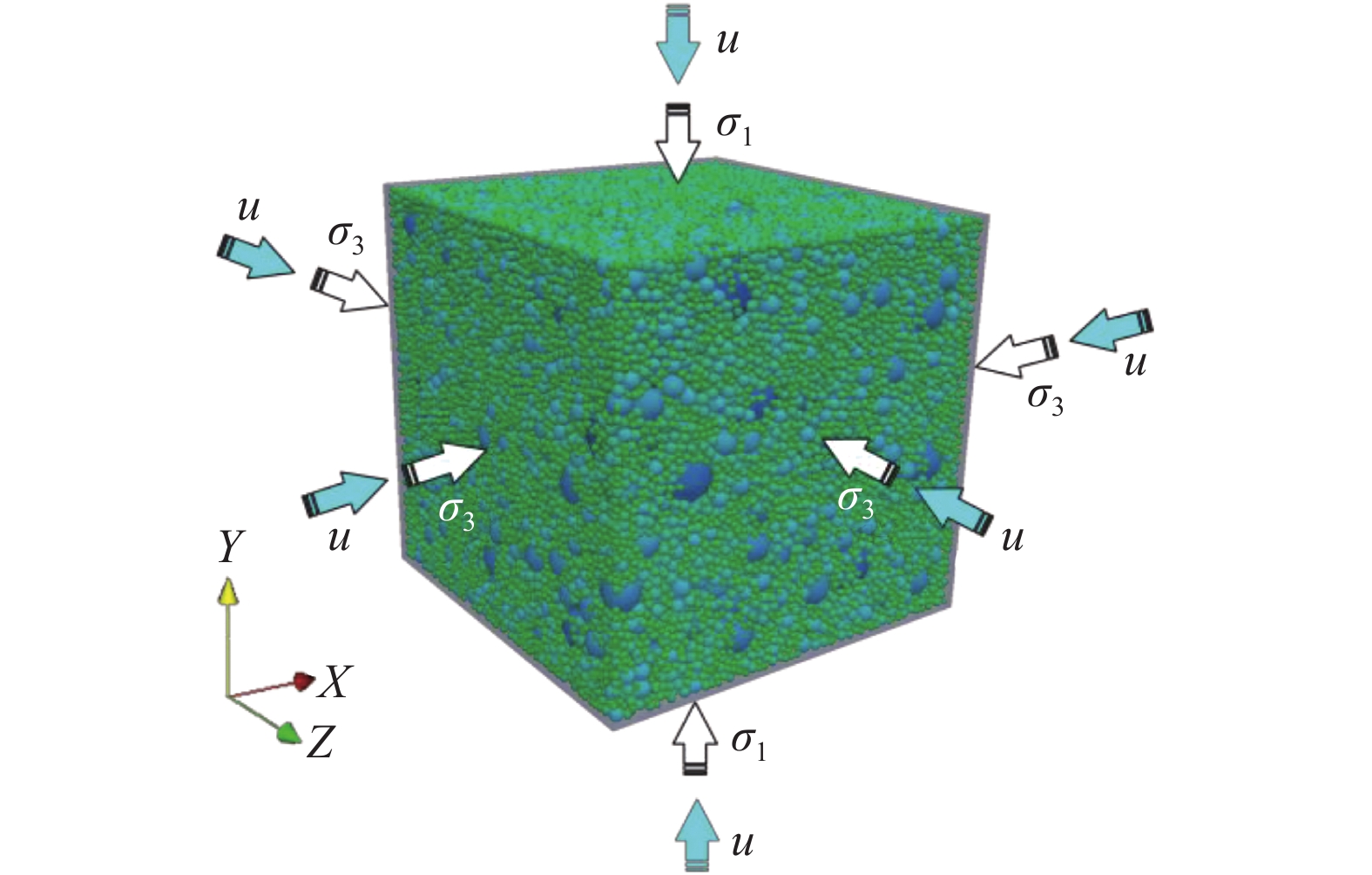 |
| 图3 模型图及边界条件 Fig. 3 Model and boundary condition |
相同级配条件下的直剪试验测得内摩擦角为31.7°。无黏性土的颗粒摩擦系数与材料摩擦系数接近,因此在模拟中依据直剪试验结果将颗粒摩擦系数设为0.62。泊松比参考既有地质资料和模拟试验结果[28]定为0.28。立方体模型受到3对无摩擦刚性墙的限制,若墙体刚度较低,与墙相邻的颗粒容易逸出[29],墙体的刚度通常比颗粒的刚度大几个数量级[30-32]。因此,确定墙体法向刚度为颗粒法向刚度的100倍。
2)等压固结
10月11日白格堰塞体平均高出江面40 m,重度为2000 kg/m3[33],因此设定400 kPa和800 kPa 两个围压值,其中400 kPa表征堰塞体中部或中下部靠近堰塞体外缘的土料,800 kPa表征堰塞体底部土料的最大围压。
在等压固结过程中,六面墙体以不超过0.2 mm/s的速度移动,当试样的应力值与预定围压400 kPa之差小于0.1%时,认为土样内部已经达到预定的应力。然后在400 kPa模型的基础上,按照同样的方法进行800 kPa的等压固结。
3)偏压固结
鉴于白格堰塞体内部的应力比难以确定,分别设定了0.50、0.75和1.00这3个应力比来表征不同的初始应力状态。
在偏压固结过程中,保持围压不变,缓慢增加轴向压力,直至达到既定初始应力状态为止。
2.2 水位条件白格堰塞湖溃前水位最高上升36.4 m,最大孔隙水压力为364 kPa。模拟过程中,流体边界条件设为压力边界,且立方体各面的流体压力量值同步增加(图3)。初始流体压力边界条件设为0 kPa,然后每200时间步更新一次,经过20万步后,增加至最大孔隙水压力364 kPa。模拟应力路径如图4所示。其中失稳线(IL)依据材料的峰值强度确定。
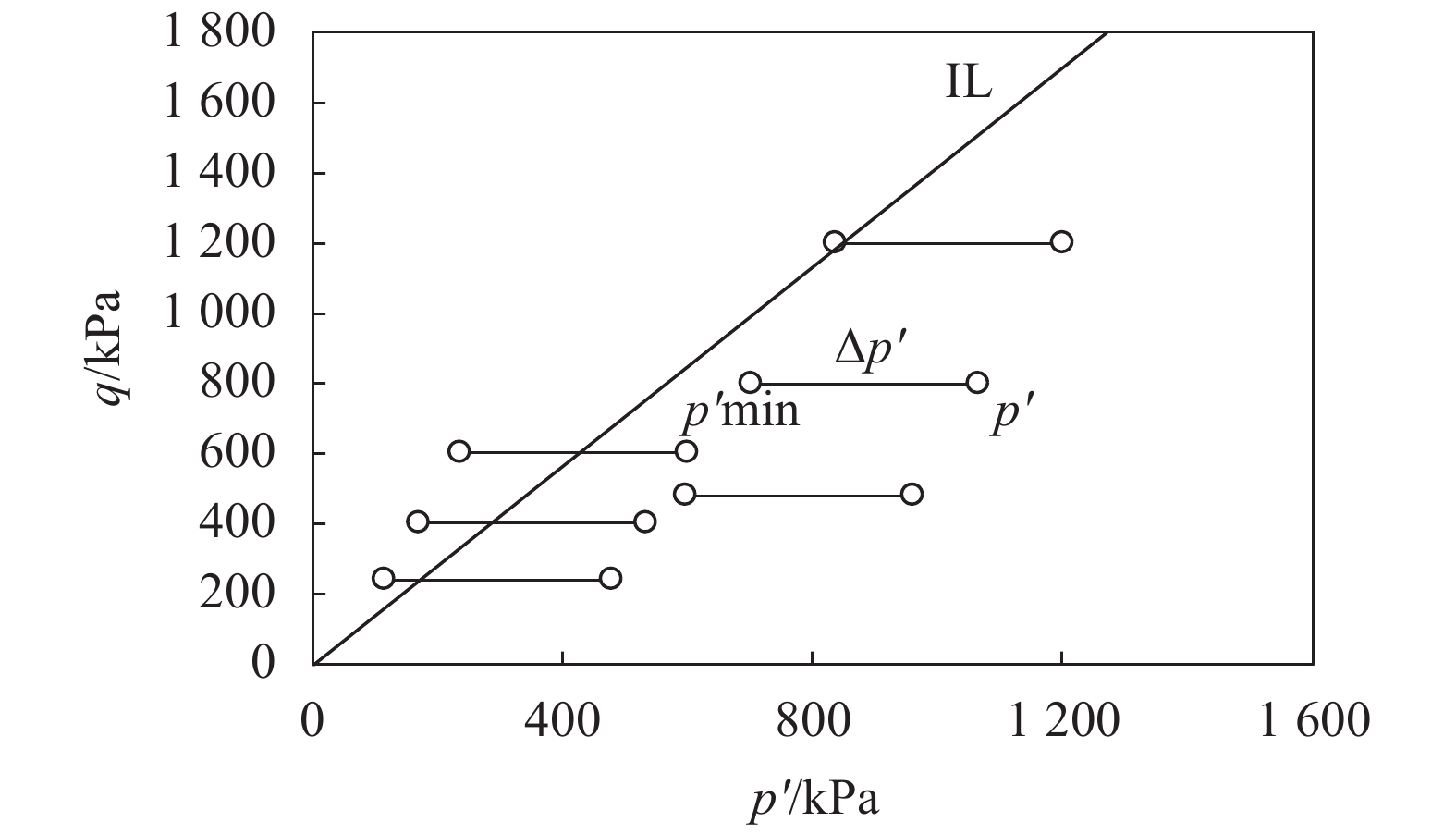 |
| 图4 模拟应力路径 Fig. 4 Stress path of simulation |
3 模拟结果 3.1 应力比变化规律
图5为400 kPa和800 kPa两种围压条件下,应力比q/p'随平均有效应力p'的变化曲线,其中图5(a)及以下各图中的黑色实心填充点均为初始围压400 kPa条件下孔压达到200 kPa时的数据。
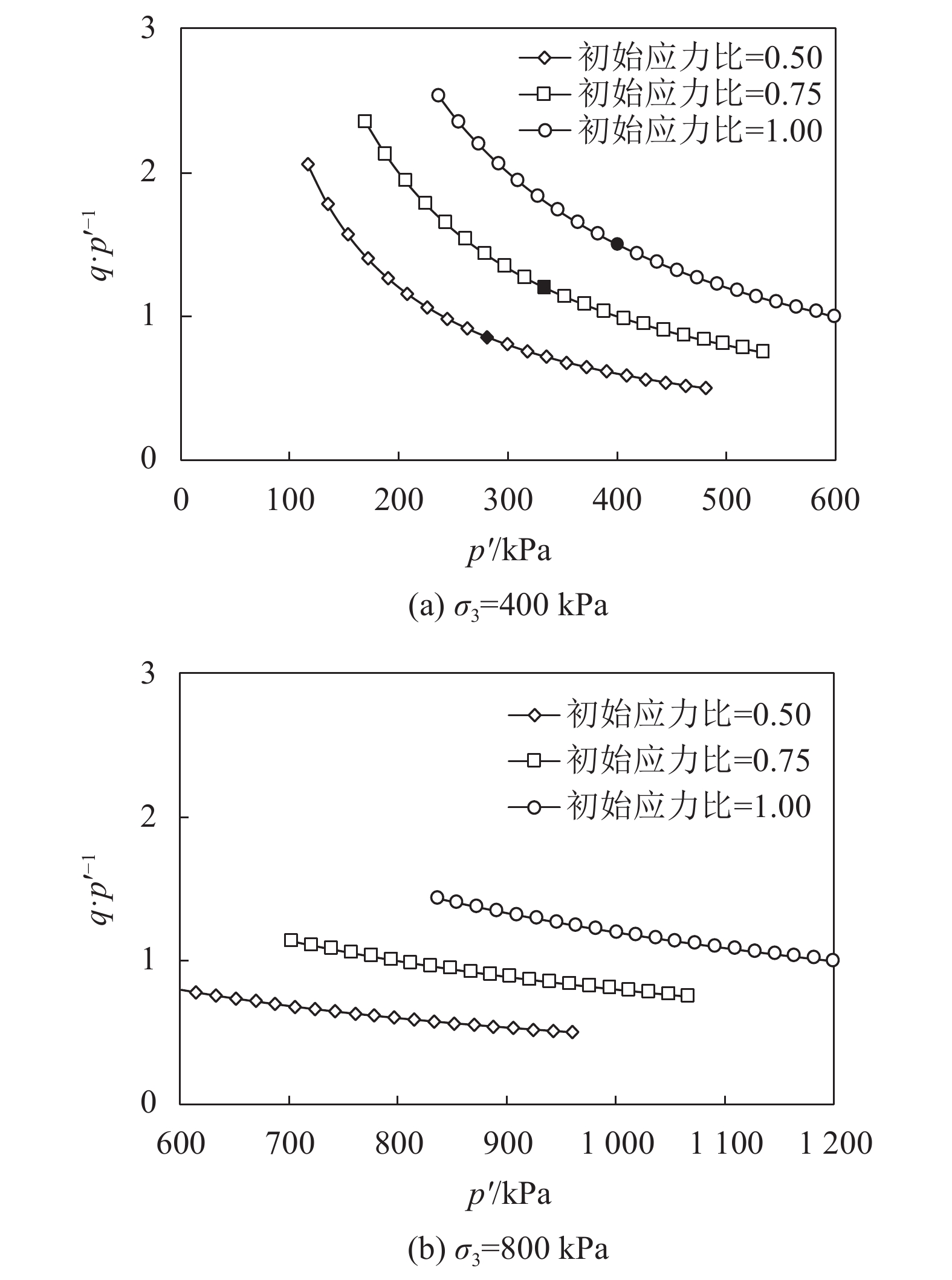 |
| 图5 q/p'随p'变化曲线 Fig. 5 Relationship between q/p' and p' |
从图5中可以看出:
1)同一围压条件下,不同初始应力比之间q/p'与p'的关系相近,应力比增加速率基本相同。
2)在初始阶段,随着孔压的增大,平均有效应力不断降低,应力比逐渐增大,且基本呈线性增大;当孔压增长到一定值后,平均有效应力与应力比呈现非线性关系,且随着平均有效应力的降低,应力比增幅加大(图5(a))。
3.2 宏观变形规律湖水位壅高条件下的宏观变形规律主要是通过图2所示的不同应力路径条件下的轴应变及体应变的变化规律,分析堰塞体各位置因初始应力条件和孔压变化范围的不同而展现出不同的变形特征。
1)轴应变特征
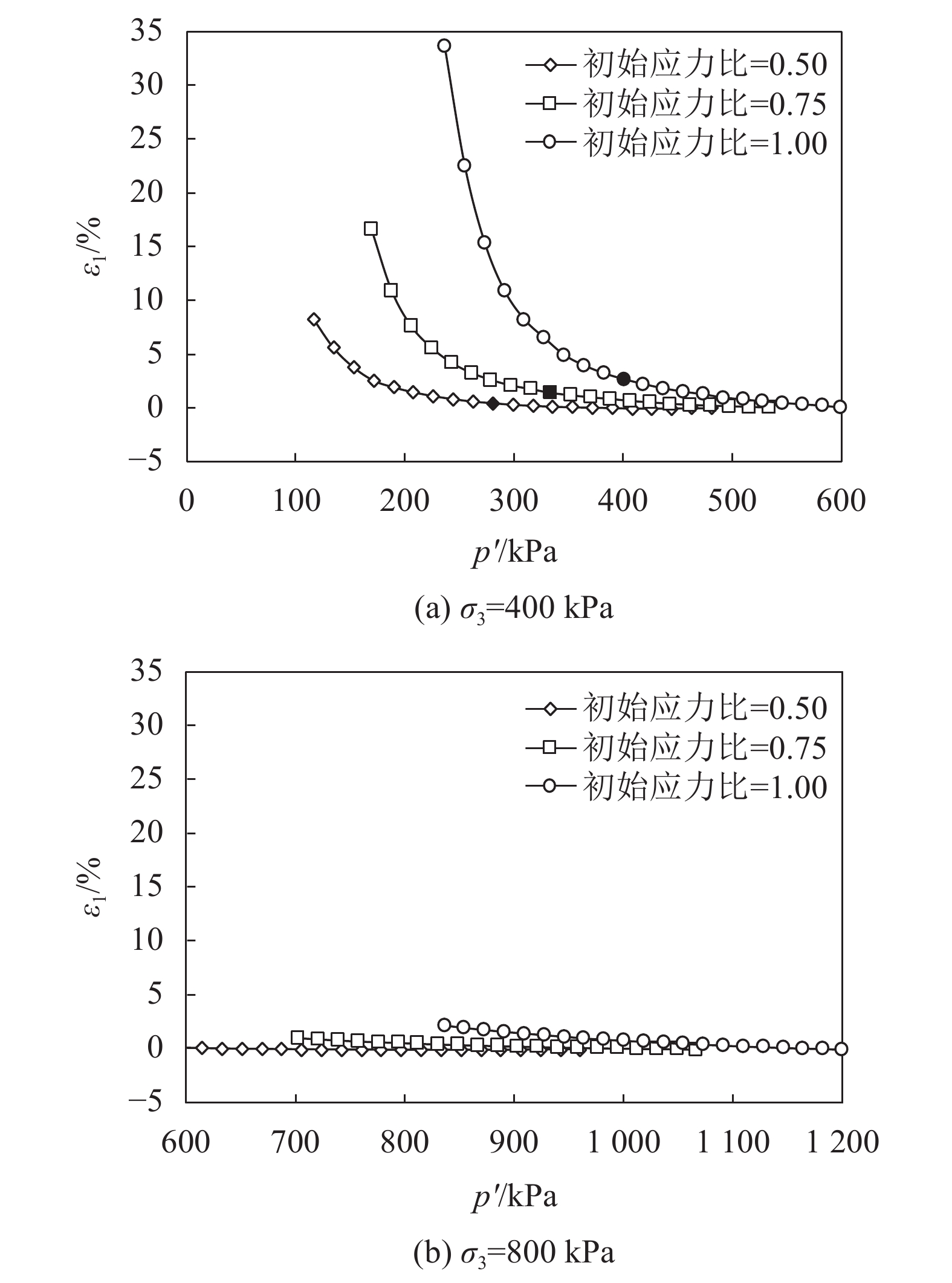
图6为400 kPa和800 kPa两种围压条件下,初始应力比分别为0.50、0.75和1.00时,轴应变
 |
|
图6 |
在400 kPa的围压下,当孔压达到200 kPa时,平均有效应力与轴向应变基本呈线性关系,且初始应力比越高,轴向应变越大,但轴向应变整体量值偏小,不超过3%。当孔压超过200 kPa后,平均有效应力与轴向应变之间开始呈现非线性关系,并且初始应力比越高,越早呈现非线性关系,且最大轴向应变接近35%。
在800 kPa的围压下,在漫顶之前,即孔压达到364 kPa时,水位的抬升会略微增加轴向应变,但整体量值较小,不超过3%,且平均有效应力与轴向应变基本成线性关系。在800 kPa的围压下,平均有效应力与轴向应变线性变化阶段的规律与400 kPa围压下的相同,均是初始应力比越大,该线性曲线的坡比越陡。
在堰塞体内部的应力状态分布中,同一高程条件下,靠近边缘位置的围压变小,应力比增大。据此对比分析400 kPa和800 kPa围压下的平均有效应力与轴向应变关系图,可以推测,在堰塞体中部,漫顶之前水位的抬升会带来轴向应变的增加,但应变量较小;在接近堰塞体边缘,在相同的平均有效应力下,抬升的水位较高,从而会导致较大的应变。
2)体应变特征
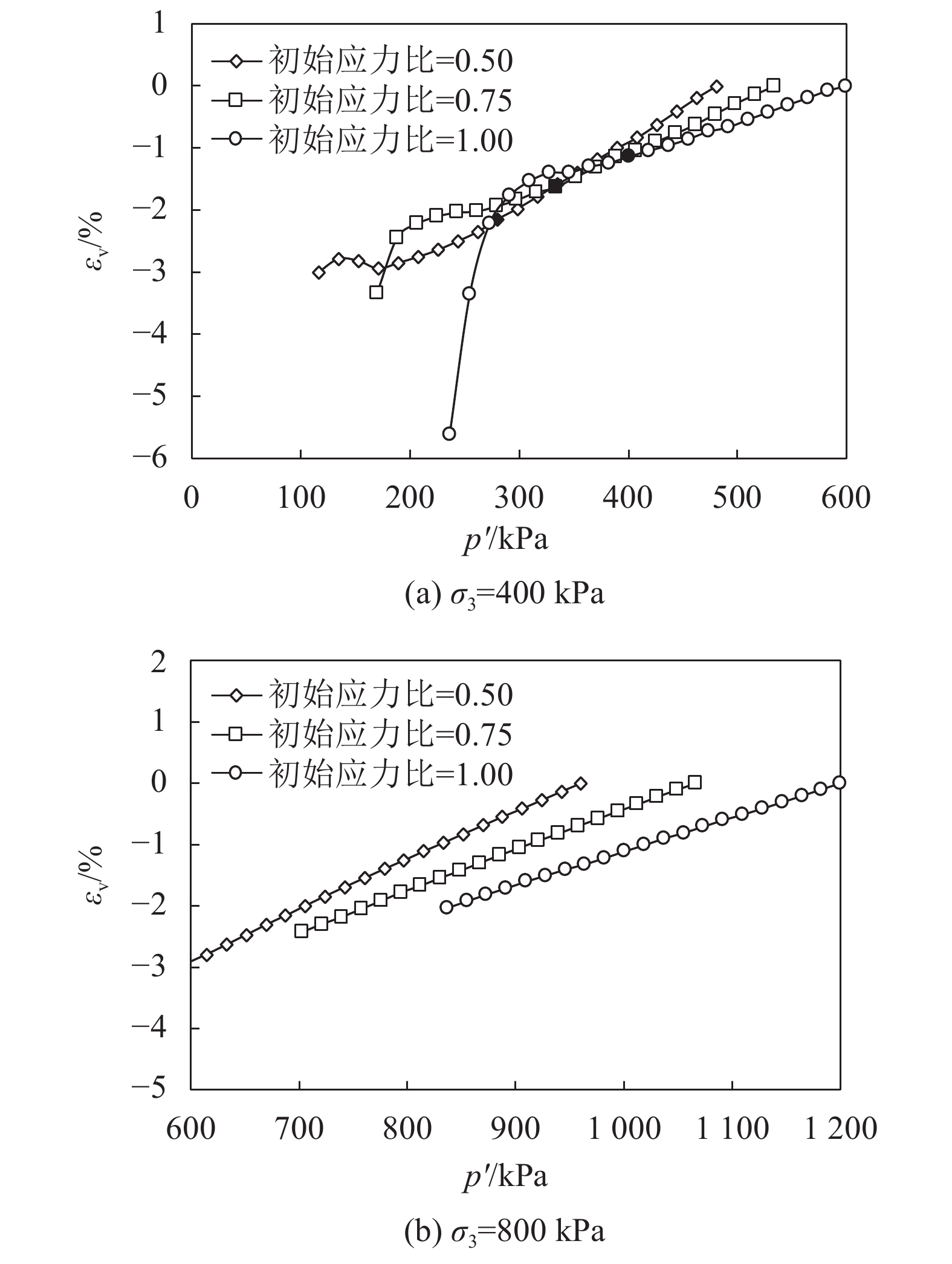
图7为400 kPa和800 kPa两种围压条件下,初始应力比分别为0.50、0.75和1.00时,体应变εv随平均有效应力变化的曲线。在线性变化阶段,400 kPa和800 kPa围压条件下的规律基本相同,均是初始应力比越大,坡比越缓,且最终的体应变越小。
 |
|
图7 |
在400 kPa的围压下,随着孔隙水压力的增加,体应变会由线性变化阶段转化到非线性变化阶段,并且初始应力比越高,体应变越大。在400 kPa的围压下,应力比越大,体应变εv随平均有效应力变化的曲线达到拐点时的孔隙水压力越小。这表明在相同的孔隙水压力条件下,应力比越大,土样越容易发生破坏。
在孔压增加过程中,随着平均有效应力的降低,体应变均呈现出增大的特征,但具体量值较小,这表明随着水位的壅高堰塞体体积可能会因平均有效应力降低而略微增加。
3)轴应变与体应变关系
图8为400 kPa和800 kPa两种围压条件下,体应变
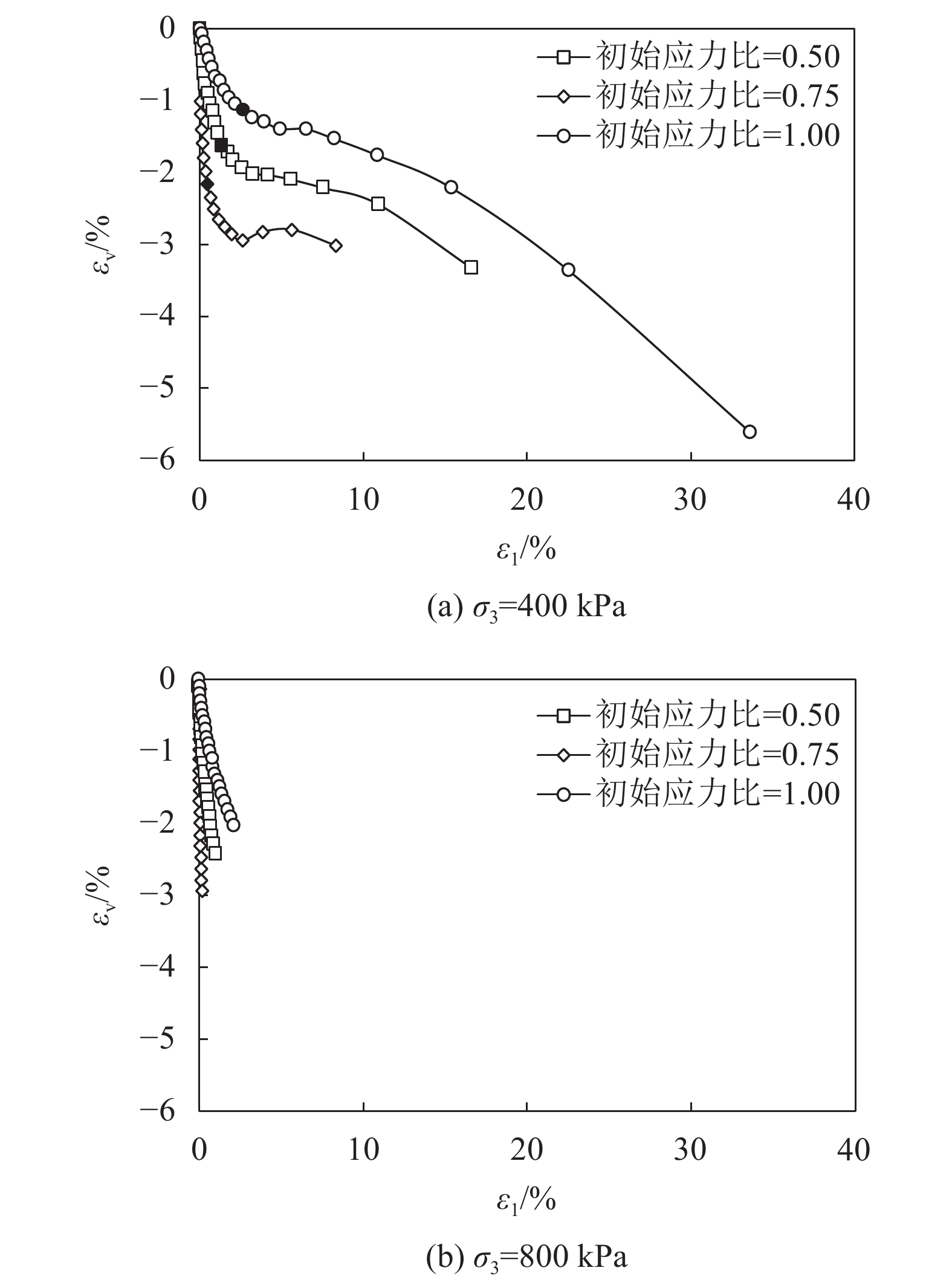 |
|
图8 |
3.3 微观力学机理
堰塞体主要为颗粒物质构成,颗粒之间的接触力链构成颗粒物质的骨架,是确定颗粒物质力学性质的主要因素[34]。分析颗粒接触力概率分布,有助于从统计角度认识颗粒的接触力链分布规律及颗粒物质力学性质的变化。
图9分别为围压400 kPa和800 kPa条件下归一化法向力fn/<fn>的概率密度函数P(fn),其中,fn为颗粒间法向接触力,<fn>为颗粒间平均法向接触力。
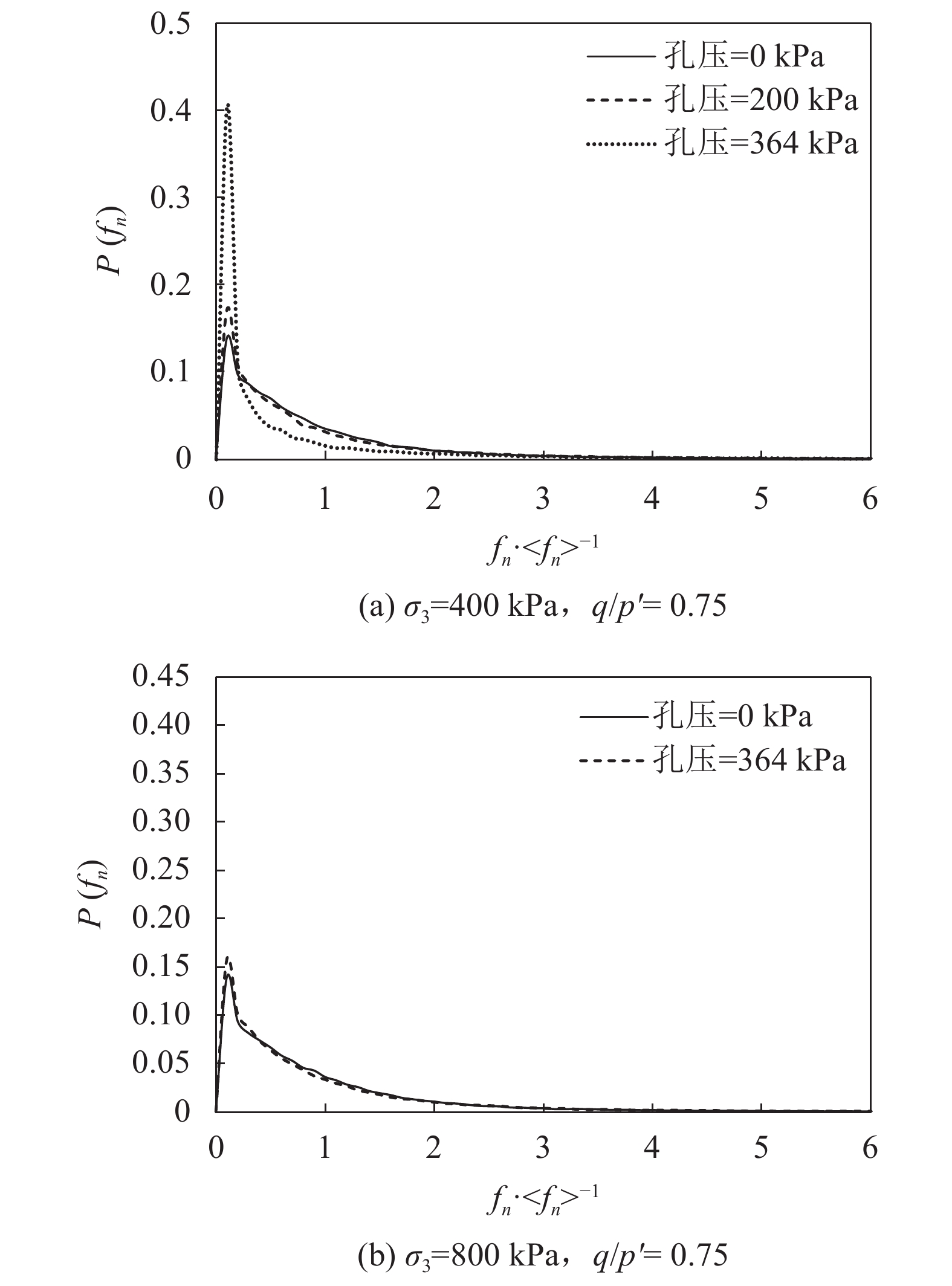 |
| 图9 颗粒接触力分布规律 Fig. 9 Normalized normal contact force distribution |
图10为400 kPa围压下、初始应力比为0.75的接触力云图。因为相同围压条件下,不同初始应力比的概率密度函数基本相同,这里仅列出初始应力比q/p'= 0.75条件下的概率密度函数进行对比分析。
 |
|
图10 |
不同围压条件下,在施加孔隙水压力之前,接触力概率密度函数基本相同,均是在fn/<fn>=0.1位置的概率密度最大,这表明该模拟中的概率密度函数受围压和初始应力比的影响较小。接触力分布云图中(图10(a)),强接触力的方向与最大主应力的方向基本一致,而弱接触力的分布方向受最大主应力影响相对较小,在各个方向都有分布。
施加孔隙水压力过程中,在达到失稳线之前,随着孔压的增长,接触力概率密度函数略有变化,均只是fn/<fn>=0.1位置的概率略有增加,但增加量较小。这表明该模拟中的概率密度函数在孔压增加的初始阶段受孔压的影响较小。在接触力分布云图中(图10(b)),强接触的位置与方向变化相对而小,而弱接触力的分布却产生了明显变化,水平向的接触力明显变稀,减少。
随着孔隙水压力的增大,在应力路径越过失稳线后,概率密度函数产生了较大的变化,弱接触力链(fn/<fn><1)的概率大幅增加,其中fn/<fn>=0.1位置的概率急剧增加约2.4倍,强接触力链(fn/<fn>>1)概率显著降低。这表明在经过失稳线后,材料的微观结构产生了较大的变化。从而导致较大变形。在接触力分布云图中(图10(c)),强弱接触的位置与方向均产生了较大的变化,垂向的弱接触力减少,水平向的弱接触力更是大幅减少,显著抽稀,整体的接触力分布明显以竖向为主。
4 结 论以白格堰塞体为实例,通过基于DEM–PFV的流固耦合模拟方法,开展了湖水位壅高条件下的堰塞体土料常剪应力剪切试验敏感性数值模拟,分析了湖水位壅高过程中的堰塞体土料的变形特性。
研究表明湖水位壅高条件下堰塞体土料变形特性与土料在堰塞体中的位置紧密相关。相同围压条件下,接近堰塞体上游外缘的土料初始应力比高、抬升水位高,更易在湖水位壅高过程中穿过失稳线,导致颗粒之间的接触力分布结构产生较大的变化,并引发较大的变形,甚至破坏。并且大变形区的厚度与范围受到初始应力状态及最高湖水位条件的限制。
敏感性模拟中,不同应力路径下所采用的颗粒摩擦系数均相同,以此分析堰塞体土料的变形时,暗含了均匀性的假设。实际上堰塞体具有较强的非均匀性,这会导致模拟结果与实际存在一定误差,但这不影响本研究中的规律性成果。
研究成果表明,DEM–PFV流固耦合方法可以较好地模拟室内试验过程,不仅可以模拟出宏观现象变化,还可以观察常剪应力路径中的微观结构变化,有助于从微观尺度分析常剪应力路径下各宏观现象的机理。
| [1] |
Nie Gaozhong,Gao Jianguo,Deng Yan. Preliminary study on earthquake induced dammed lake[J]. Chinese Journal of Quaternary Sciences, 2004, 24(3): 293-301. [聂高众,高建国,邓砚. 地震诱发的堰塞湖初步研究[J]. 第四纪研究, 2004, 24(3): 293-301. DOI:10.3321/j.issn:1001-7410.2004.03.008] |
| [2] |
Yang Yang,Cao Shuyou. Experimental study on breach growth mechanisms of natural barrier dams[J]. Chinese Journal of Hydraulic Engineering, 2012, 43(Supp2): 60-67. [杨阳,曹叔尤. 堰塞坝溃决机理试验研究[J]. 水利学报, 2012, 43(增刊2): 60-67. DOI:10.13243/j.cnki.slxb.2012.s2.001] |
| [3] |
Xing Aiguo,Xu Nana,Song Xinyuan. Numerical simulation of lake water down-stream flooding due to sudden breakage of Yigong landslide dam in Tibet[J]. Chinese Journal of Engineering Geology, 2010, 18(1): 78-83. [邢爱国,徐娜娜,宋新远. 易贡滑坡堰塞湖溃坝洪水分析[J]. 工程地质学报, 2010, 18(1): 78-83. DOI:10.3969/j.issn.1004-9665.2010.01.011] |
| [4] |
Chen Zuyu,Zhang Qiang,Hou Jingming,et al. Back analysis on dam-breach flood of "10·10" Baige barrier lake on Jinsha River[J]. Yangtze River, 2019, 50(5): 1-4. [陈祖煜,张强,侯精明,等. 金沙江“10·10”白格堰塞湖溃坝洪水反演分析[J]. 人民长江, 2019, 50(5): 1-4. DOI:10.16232/j.cnki.1001-4179.2019.05.001] |
| [5] |
Costa J E,Schuster R L. The formation and failure of natural dams[J]. Geological Society of America Bulletin, 1988, 100(7): 1054-1068. DOI:10.1130/0016-7606(1988)100<1054:TFAFON>2.3.CO;2 |
| [6] |
Sun Qicheng,Wang Guangqian,Hu Kaiheng. Quake lakes in the Wenchuan Earthquake and challenging mechanical problems[J]. Chinese Journal of Physics, 2009, 38(4): 248-253. [孙其诚,王光谦,胡凯衡. 汶川地震堰塞体及相关力学问题[J]. 物理, 2009, 38(4): 248-253. DOI:10.3321/j.issn:0379-4148.2009.04.005] |
| [7] |
Chang D S,Zhang L M,Xu Y,et al. Field testing of erodibility of two landslide dams triggered by the 12 May Wenchuan earthquake[J]. Landslides, 2011, 8(3): 321-332. DOI:10.1007/s10346-011-0256-x |
| [8] |
Okeke A C U,Wang F. Critical hydraulic gradients for seepage-induced failure of landslide dams[J]. Geoenvironmental Disasters, 2016, 3(1): 9. DOI:10.1186/s40677-016-0043-z |
| [9] |
Liu Handong,Li Xiaochao,Liu Shun,et al. Zhouqu catastrophic mudslide barrier dam stability analysis[J]. Yellow River, 2013, 35(8): 116-119. [刘汉东,李小超,刘顺,等. 舟曲特大山洪泥石流堰塞坝稳定性分析[J]. 人民黄河, 2013, 35(8): 116-119. DOI:10.3969/j.issn.1000-1379.2013.08.037] |
| [10] |
Chai Hejun,Dong Yun,Li Shaoxuan,et al. Analysis of natural rock filled dam break mode and environmental affections[J]. Chinese Journal of Geological Hazards and Environment Preservation, 2005, 16(2): 172-176. [柴贺军,董云,李绍轩,等. 大型天然土石坝的溃坝方式及环境效应分析[J]. 地质灾害与环境保护, 2005, 16(2): 172-176. DOI:10.3969/j.issn.1006-4362.2005.02.014] |
| [11] |
Ma J,Xiong X,Yang J,et al. Element tests on hydraulic-mechanical behavior of saturated/unsaturated landslide dam materials[J]. Japanese Geotechnical Society Special Publication, 2020, 8(9): 360-365. DOI:10.3208/jgssp.v08.j30 |
| [12] |
Yang Jiangtao,Shi Zhenming,Zhang Qingzhao,et al. Discrete element method (DEM) study on mechanical properties of dam materials[J]. Chinese Journal of Engineering Geology, 2018, 26(Supp1): 631-638. [杨江涛,石振明,张清照,等. 堰塞坝坝体材料力学特性的离散元方法 (DEM) 研究[J]. 工程地质学报, 2018, 26(增刊1): 631-638. DOI:10.13544/j.cnki.jeg.2018192] |
| [13] |
Chu J,Leong W K,Loke W L,et al. Instability of loose sand under drained conditions[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2012, 138(2): 207-216. DOI:10.1061/(asce)gt.1943-5606.0000574 |
| [14] |
Dong Quanyang,Cai Yuanqiang,Wang Jun,et al. Experimental study of instability of loose sand[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(3): 623-630. [董全杨,蔡袁强,王军,等. 松散砂土不稳定性试验研究[J]. 岩石力学与工程学报, 2014, 33(3): 623-630. DOI:10.13722/j.cnki.jrme.2014.03.022] |
| [15] |
Monkul M M,Yamamuro J A,Lade P V. Failure,instability,and the second work increment in loose silty sand[J]. Canadian Geotechnical Journal, 2011, 48(6): 943-955. DOI:10.1139/t11-013 |
| [16] |
Xu Qiang,Zheng Guang,Li Weile,et al. Study on successive landslide damming events of Jinsha River in Baige Village on Octorber 11 and November 3,2018[J]. Chinese Journal of Engineering Geology, 2018, 26(6): 1534-1551. [许强,郑光,李为乐,等. 2018年10月和11月金沙江白格两次滑坡-堰塞堵江事件分析研究[J]. 工程地质学报, 2018, 26(6): 1534-1551. DOI:10.13544/j.cnki.jeg.2018-406] |
| [17] |
Cundall P A,Strack O D L. A discrete numerical model for granular assemblies[J]. Géotechnique, 1979, 29(1): 47-65. DOI:10.1680/geot.1979.29.1.47 |
| [18] |
Šmilauer V,Chareyre B.Dem formulation[EB/OL].(2015-11-19) [2020-04-16].http://yade-dem.org/doc/.
|
| [19] |
Šmilauer V,Catalano E ,Chareyre B,et al.Yade Documentation 2nd ed[EB/OL].(2015-11-20) [2020-04-16].http://yade-dem.org/doc/ DOI:10.5281/zenodo.34073.
|
| [20] |
Catalano E,Chareyre B,Cortis A,et al.A pore-scale hydro-mechanical coupled model for geomaterials[C]//Particles 2011 II International Conference on Particle-Based Methods.Barcelona:CIMNE,2011:798–809.
|
| [21] |
Catalano E,Chareyre B,Barthélemy E. Pore-scale modeling of fluid-particles interaction and emerging poromechanical effects[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2014, 38(1): 51-71. DOI:10.1002/nag.2198 |
| [22] |
Chareyre B,Cortis A,Catalano E,et al. Pore-scale modeling of viscous flow and induced forces in dense sphere packings[J]. Transport in Porous Media, 2012, 92(2): 473-493. DOI:10.1007/s11242-011-9915-6 |
| [23] |
Tsuji Y,Kawaguchi T,Tanaka T. Discrete particle simulation of two-dimensional fluidized bed[J]. Powder Technology, 1993, 77(1): 79-87. DOI:10.1016/0032-5910(93)85010-7 |
| [24] |
Hosn R A,Sibille L,Benahmed N,et al. A discrete numerical model involving partial fluid-solid coupling to describe suffusion effects in soils[J]. Computers and Geotechnics, 2018, 95: 30-39. DOI:10.1016/j.compgeo.2017.11.006 |
| [25] |
Wautier A,Bonelli S,Nicot F. DEM investiga-tions of internal erosion:Grain transport in the light of micromechanics[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2019, 43(1): 339-352. DOI:10.1002/nag.2866 |
| [26] |
Tong A T,Luong N H P.Numerical model of hydro–mechanical coupling DEM–PFV and application for simulation of settlement of soil saturated in embankment due to static loading[M].CIGOS 2019,Innovation for Sustainable Infrastructure.Singapore:Springer,2020:745-750.
|
| [27] |
Zhang F,Li M,Peng M,et al. Three-dimensional DEM modeling of the stress–strain behavior for the gap-graded soils subjected to internal erosion[J]. Acta Geotechnica, 2019, 14(2): 487-503. DOI:10.1007/s11440-018-0655-4 |
| [28] |
Zhao Chuan,Jiang Linlin,Li Xiaopeng,et al. Sliding features of “10·11” largescale landslide in Jinsha River based on DEM[J]. Journal of Shenyang University, 2019, 31(4): 324-330. [赵川,蒋琳琳,李晓鹏,等. 基于DEM的“10·11”金沙江大型山体滑坡运动特性分析[J]. 沈阳大学学报(自然科学版), 2019, 31(4): 324-330. DOI:10.16103/j.cnki.21-1583/n.2019.04.012] |
| [29] |
O’Sullivan C.Particulate discrete element modelling:A geomechanics perspective[M].Boca Raton:CRC Press,2011.
|
| [30] |
Minh N H,Cheng Y P. A DEM investigation of the effect of particle-size distribution on one-dimensional compression[J]. Géotechnique, 2013, 63(1): 44-53. DOI:10.1680/geot.10.p.058 |
| [31] |
Minh N H,Cheng Y P,Thornton C. Strong force networks in granular mixtures[J]. Granular Matter, 2014, 16(1): 69-78. DOI:10.1007/s10035-013-0455-3 |
| [32] |
Gong J,Liu J,Cui L. Shear behaviors of granular mixtures of gravel-shaped coarse and spherical fine particles investigated via discrete element method[J]. Powder Technology, 2019, 353: 178-194. DOI:10.1016/j.powtec.2019.05.016 |
| [33] |
Wang Lichao,Wen Mingsheng,Feng Zhen,et al. Researches on the Baige landslide at Jinshajiang River,Tibet,China[J]. The Chinese Journal of Geological Hazard and Control, 2019, 30(1): 1-9. [王立朝,温铭生,冯振,等. 中国西藏金沙江白格滑坡灾害研究[J]. 中国地质灾害与防治学报, 2019, 30(1): 1-9. DOI:10.16031/j.cnki.issn.1003-8035.2019.01.01] |
| [34] |
孙其诚,厚美瑛,金峰.颗粒物质物理与力学[M].北京:科学出版社,2011.
|
 2020, Vol. 52
2020, Vol. 52