长期以来,学者们认为基于失速颤振和经典颤振的挥舞/摆振/扭转耦合位移的发散不稳定运动是回转叶片(如风力机和直升机叶片)结构断裂失效的重要原因,其中挥舞/扭转(弯扭)运动造成的失效是其中表现之一[1-2]。而近年来,尾缘襟翼结构被广泛用于叶片气弹减载和颤振控制。Haselbach[3]提出了一种基于壳体单元模型的先进叶片建模方法,其中尾缘区域中的粘结线通过实心砖元件离散化,这可以提高风轮机叶片的结构预测的可靠性。Llorente等[4]提出了一种新的实验方法,重点研究了具有尾缘锯齿的风力机叶片的空气动力性能的变化,以及具体的设计过程和预测方法。Chen等[5]设计了一种尾缘流量控制装置并讨论了其性能,包括通过求解旋转框架内的3维雷诺平均方程,在风轮上安装微插片并在尾缘设计微射流单元,以达到减载目的。张文广等[6]以NREL–5MW风力机为研究对象,实现了智能叶片风力机建模及多目标尾缘襟翼控制,研究了尾缘襟翼在风力机主动降载和功率控制方面的效果。张广兴[7]将风力机叶片描述为展向分布尾缘襟翼的复合材料悬臂梁叠层板,通过瑞利–里茨法实现了结构建模,建立了气弹模型,实现了振动频率分析和主动振动控制。穆安乐等[8]将风力机叶片简化为展向分布尾缘襟翼的复合材料悬臂梁叠层板,通过瑞利–里茨法实现了结构建模,并结合Theodorsen气动力,建立了气弹模型,最后采用模型预测控制算法实现了主动振动控制。
然而很少有学者注意到造成叶片断裂失效的隐性故障:在常规工况下,一种由于长期处于“低幅–高频率”振动[9-10]条件下的叶片,会形成隐性的裂纹缺陷,该缺陷使得叶片体在极端颤振条件下,更容易造成断裂失效。该高频振动在湍流时的尾缘处容易产生[10],或者在柔性叶片的气动力矩表现为低幅、高频振荡[11]时的失速状态下容易产生。Zuheir等[12]也基于有限元分析,证实了尾缘处存在的低幅、高频振动效应。
作者项目组成员在前期工作中发现:高频信号的可能频率范围确定为复合材料层合结构的2阶至5阶固有频率之间。其一,当外因激励频率小于复合材料叶片的1阶固有频率时,不会发生持续的等幅高频振动(1阶频率时的共振)现象,而当外因激励频率等于复合材料叶片的1阶固有频率时,可以发生共振,但不会出现微幅共振现象;其二,当外因激励频率大于叶片的6阶固有频率时,将不会有共振现象发生,而可能发生发散不稳定现象,同时在解耦算法Galerkin法[12]的应用中,对于风力机复合材料叶片而言,Galerkin法的保留振型在5阶范围内即可以充分满足精度要求。
由于振动的高频特性,诸多智能控制算法由于迭代次数太大或者寻优难度问题而失效;一般的线性控制方法,也仅仅能进一步实现幅度的衰减,在抑制高频方面效果较弱。作者基于一种沿叶片展长分布的尾缘襟翼结构,经由步进电机驱动,并通过基于LMI设计的H∞控制方法,实现了“低幅–高频”振动控制。其实质是:通过加入步进电机硬件,并结合鲁棒控制方法,改变了整个气弹系统的频率结构,在相同的外界激励情况下,使得新系统能够避开原来气弹系统的2阶至5阶固有频率范围内的共振。
1 气弹系统方程为简化复合材料结构参数的计算,叶片采用固定弦长的实心复合材料叶片梁,翼型采用二次拟合的NACA64418翼型[13],如图1所示。
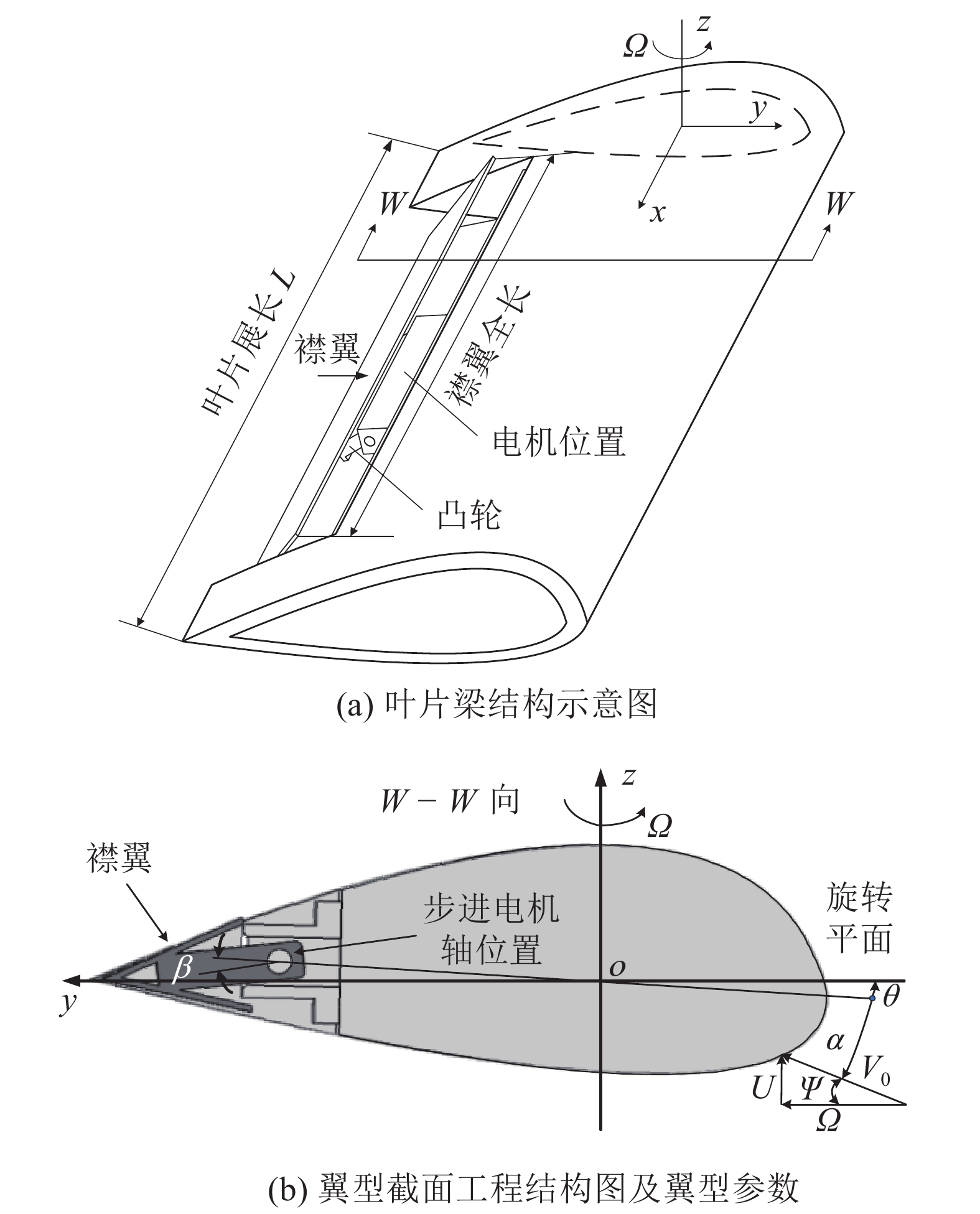 |
| 图1 叶片梁结构及翼型运动参数 Fig. 1 Structure of blade beam and airfoil motion parameters |
图1中:
复合材料铺层,以弦向为对称,采用基于周向反对称刚度(CAS)的铺层设计。在CAS铺层下,叶片展现单一的弯扭耦合位移,即挥舞/扭转耦合位移[14]。则单一截面的挥舞
| $ \begin{aligned}[b] &\left[ {{{GJ}} + \frac{1}{2}{m_{\rm{c}}}{\varOmega ^2}K_{\rm{A}}^2\left( {{L^2} - {x^2}} \right)} \right]\theta '' + {K_{\rm{c}}}{\textit{z}}''' -\\ & \;\;\;\;\;\;{m_{\rm{c}}}{\varOmega ^2}K_{\rm{A}}^2x\theta ' - {m_{\rm{c}}}K_{\rm{m}}^2\ddot \theta'' - {m_{\rm{c}}}{\varOmega ^2}\left( {K_{{\rm{m}}2}^2 - K_{{\rm{m}}1}^2} \right)-\\ & \;\;\;\;\;\; {m_{\rm{c}}}{\varOmega ^2}\left( {K_{{\rm{m}}2}^2 - K_{{\rm{m}}1}^2} \right)\theta = M \end{aligned} $ | (1) |
| $ \begin{aligned}[b] {K_{\rm{c}}}\theta ''' + EI{\textit{z}}'''' +& {m_{\rm{c}}}\ddot {\textit{z}} - \frac{1}{2}{m_{\rm{c}}}{\varOmega ^2}\left[ {{\textit{z}}''} \left( {{L^2} - {x^2}}\right)+\right. \\ &\Big. { {\textit{z}}'\left( { - 2x} \right)} \Big] = F \end{aligned} $ | (2) |
式中,
文献[15]展示了一种悬臂振动2D翼型的基于尾缘襟翼的准稳态气动力。作者将文献[15]中襟翼激励气动方程中的绝对风速改为风力机的相对风速,将其中的变桨角度替换为风力机叶片的攻角
| $ {\;\;\;\;\;\begin{aligned}[b] F =& \frac{1}{2}{\rho _{\rm{a}}}\bigg\{ {\text{π} b[{V_0}(\ddot {\textit{z}}/{V_0} - \dot \theta ) - b\ddot \theta /2]}+ \bigg.\\ & \left. {2\text{π} \dot {\textit{z}} + 2\text{π} \bigg[V_0^2\frac{{{C_{{\rm{l}}\beta }}}}{{{C_{{\rm{l}}\alpha }}}}(\psi + 1)\beta - V_0^2\frac{{{C_{{\rm{l}}\beta }}}}{{{C_{{\rm{l}}\alpha }}}}\theta- b{V_0}\dot \theta \bigg]} \right\} \end{aligned}} $ | (3) |
| $ \begin{aligned}[b] M = {\rho _{\rm{a}}}b\bigg[\frac{{\text{π} b{V_0}(\dot \theta - \ddot {\textit{z}}/{V_0})}}{4} + \frac{{\text{π} b{V_0}\dot \theta }}{4} + \frac{{3\text{π} {b^2}\ddot \theta }}{{16}}\bigg] + {\rho _{\rm{a}}}\text{π} V_0^2\frac{{{C_{{\rm{m}}\beta }}}}{{{C_{{\rm{m}}\alpha }}}}\beta \end{aligned} $ | (4) |
式中:ρa为空气密度;
Galerkin法常用来离散化并求解系统(1)的偏微分方程组[12],弯扭耦合位移分别描述为:
| $ {\;\;\;\;\;\;\textit{z}}\left( {x,t} \right) = {{{{\boldsymbol{Z}}}}^{\rm{T}}}\left( x \right){q_{\textit{z}}},\;\theta \left( {x,t} \right) = {{\boldsymbol{\varTheta}} ^{\rm{T}}}\left( x \right){q_\theta } $ | (5) |
| $ \begin{array}{l} {\;\;\;\;\;\;{\boldsymbol{Z}}^{\rm{T}}}\left( x \right) = \left[ {{{\textit{z}}_1}\left( x \right), \cdots ,{{\textit{z}}_i}\left( x \right), \cdots ,{{\textit{z}}_N}\left( x \right)} \right],\\ {\;\;\;\;\;\;{\boldsymbol{\varTheta}} ^{\rm{T}}}\left( x \right) = \left[ {{\theta _1}\left( x \right), \cdots ,{\theta _i}\left( x \right), \cdots ,{\theta _N}\left( x \right)} \right] \end{array} $ | (6) |
式中,
| $ \left\{ \begin{array}{l}{\textit{z}_i}\left( x \right) = {\left( {x/L} \right)^{{\rm{1 + }}i}}\left\{ {6 + {i^2}{{\left( {1 - x/L} \right)}^2} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\left. {i\left[ {5 - 6x/L + {{\left( {x/L} \right)}^2}} \right]} \right\}/\left[ {i\left( {1 + i} \right)\left( {2 + i} \right)\left( {3 + i} \right)} \right],\\ {\theta _i}\left( x \right) = \sin \left( {i\text{π} x/L} \right)\end{array}\right. $ | (7) |
襟翼全长为
| ${{\boldsymbol{M}}_0}\ddot {\boldsymbol{X}} + {{\boldsymbol{C}}_0}\dot {\boldsymbol{X}} + {{\boldsymbol{K}}_0}{\boldsymbol{X}} = {{\boldsymbol{Q}}_0}{\boldsymbol{\beta}} $ | (8) |
式中,
将式(8)转换为1阶系统,得到:
| $\dot {\boldsymbol{Y}} = {{\boldsymbol{A}}_0}{\boldsymbol{Y}} + {{\boldsymbol{B}}_0}{\boldsymbol{\beta}} $ | (9) |
式中,状态变量
振型函数
叶片结构参数和运动参数如下:L=5 m,U=15 m/s,c=0.6 m,
| 表1 两种方法前4阶频率f 比较 Tab. 1 Comparisons of the first four-order frequencies f based on two approaches |
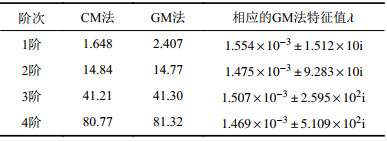 |
另外,Stefan等[17]也提出了一种精确计算悬臂结构自由振动主模态频率
| $ \begin{aligned}[b] &{\left( {2\text{π} f} \right)^2} = \frac{{ - \left( {GJ{m_{\rm{c}}}{g^2} - EI{m_{\rm{c}}}K_{\rm{m}}^2{g^4}} \right)}}{{2m_{\rm{c}}^2K_{\rm{m}}^2}} \pm \\ &\frac{{\sqrt {{{\left( {GJ{m_{\rm{c}}}{g^2} - EI{m_{\rm{c}}}K_m^2{g^4}} \right)}^2} + 4m_{\rm{c}}^2K_{\rm{m}}^2\left( {GJ \cdot EI - K_{\rm{c}}^2} \right){g^6}} }}{{2m_{\rm{c}}^2K_{\rm{m}}^2}} \end{aligned} $ | (10) |
式中,参数
从表1的结果对比可以看出:在60°铺层角时,两种方法的前4阶频率结果相近,特别是高阶次的2~4阶频率结果非常接近,高阶频率的误差不超过0.68%。同样在铺层角度(0°~90°)范围内,每隔15°计算了复合材料结构参数,分析了前3阶自由振动的频率,并将GM与CM法进行了对比,如图2所示。由图2可以看出:1阶频率均比较接近,而高阶频率的误差不超过0.7%。GM法的振型函数选择的有效性及保留振型项数
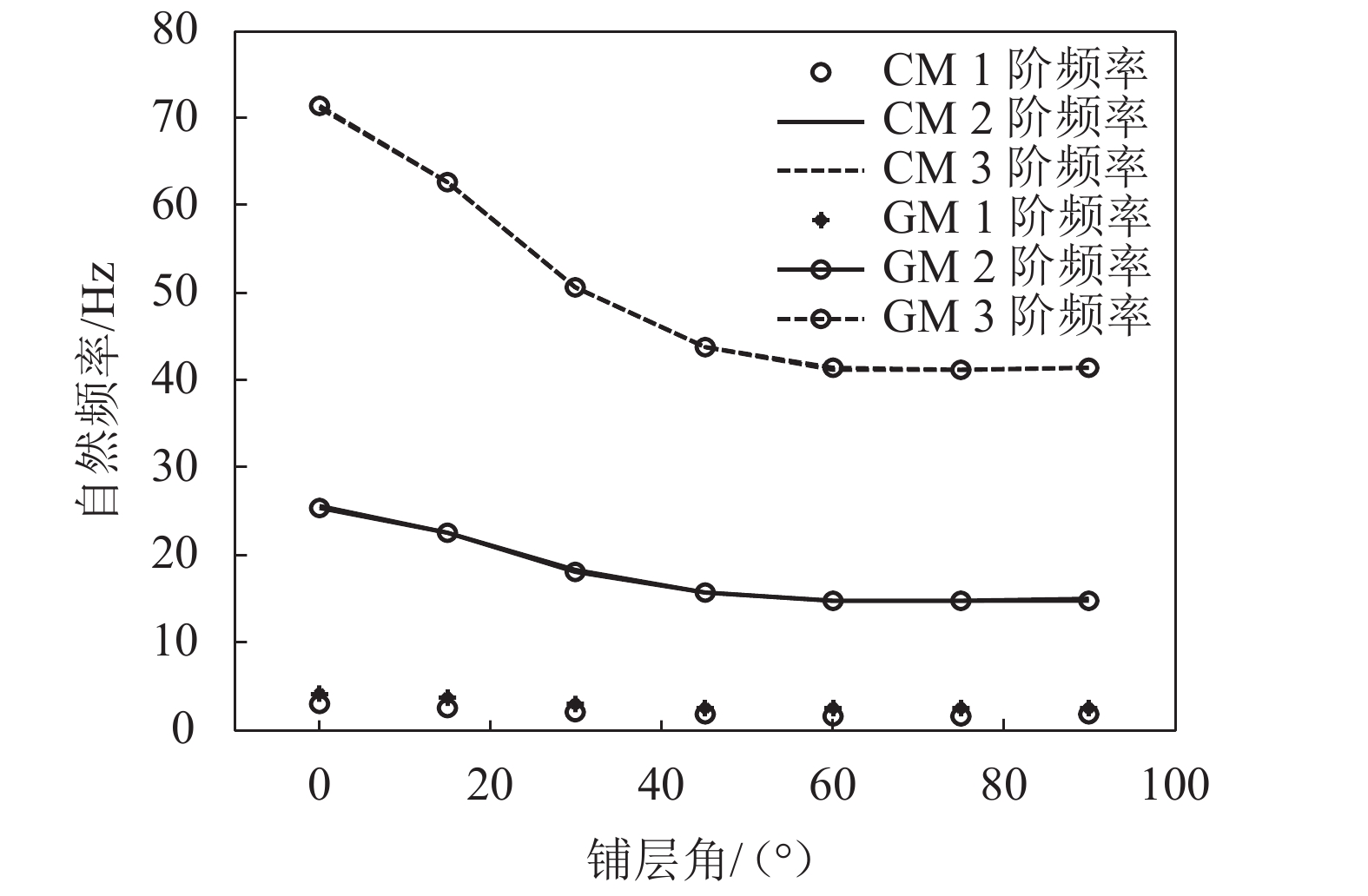 |
| 图2 前3阶自然频率对比 Fig. 2 Comparisons of the first three-order natural frequencies |
2.2 基于工程应用的方程改进
图1中的轻质结构质量可以忽略,但步进电机质量和动态驱动效应不能忽略。假设步进电机质量为
| $\left\{ {\begin{array}{*{20}{l}} {\dot {\boldsymbol{Y}} = {{\boldsymbol{A}}_0}{\boldsymbol{Y}} + {{\boldsymbol{B}}_1}\omega + {{\boldsymbol{B}}_0}{\boldsymbol{\beta}} } \\ {{\boldsymbol{Z}} = {{\boldsymbol{C}}_1}{\boldsymbol{Y}} + {{\boldsymbol{D}}_1}{\boldsymbol{\beta}} } \end{array}} \right.$ | (11) |
式中:
改进后的系统方程(11),无法通过常规的智能控制方法来求解,本设计采用一种H∞控制理论可实现优化控制。
3对于系统方程(11),给定鲁棒性能系数
| $\left[ {\begin{array}{*{20}{c}} \begin{gathered} {{\boldsymbol{A}}_0}{{\boldsymbol{P}}_1} + {{\boldsymbol{P}}_1}{\boldsymbol{A}}_0^{\rm{T}} + {{\boldsymbol{B}}_0}{{\boldsymbol{P}}_2} + {\boldsymbol{P}}_2^{\rm{T}}{\boldsymbol{B}}_0^{\rm{T}} + {\gamma ^{ - 2}}{{\boldsymbol{B}}_1}{\boldsymbol{B}}_1^{\rm{T}} \end{gathered} &{{{\left( {{{\boldsymbol{C}}_1}{{\boldsymbol{P}}_1} + {{\boldsymbol{D}}_1}{{\boldsymbol{P}}_2}} \right)}^{\rm{T}}}} \\ {{{\boldsymbol{C}}_1}{{\boldsymbol{P}}_1} + {{\boldsymbol{D}}_1}{{\boldsymbol{P}}_2}}&{ - {\boldsymbol{I}}} \end{array}} \right] < 0$ | (12) |
则H∞控制的状态反馈控制器可以设计为:
| ${\boldsymbol{\beta}} = {\boldsymbol{KY}} = {{\boldsymbol{P}}_2}{\boldsymbol{P}}_1^{ - 1}{\boldsymbol{Y}}$ | (13) |
式中,
控制目标设计为:对于任意扰动
| ${\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\int_0^\infty {\left[ {\sum\limits_{j = 1}^{4N} {Y_i^2 + {\rho ^2}{{\boldsymbol{\beta}} ^2}} } \right]} {\rm{d}}t < {\gamma ^2}\int_0^\infty {{\omega ^2}} {\rm{d}}t}$ | (14) |
式中:鲁棒控制参数
在控制输出表达式
| ${\;\;\;\;\;\;\; \boldsymbol{Z}} = {{\boldsymbol{C}}_1}{\boldsymbol{Y}} + {{\boldsymbol{D}}_1}{\boldsymbol{\beta}} = {\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{Y}}_1}}&{{{\boldsymbol{Y}}_2}}& \cdots &{{{\boldsymbol{Y}}_{4N}}}&{\rho {\boldsymbol{\beta}} } \end{array}} \right]^{\rm{T}}}$ | (15) |
因此,
| ${\;\;\;\;\;\;\;\;\;\;\;\;\;\left\| {\boldsymbol{Z}} \right\|_2^2} = \int_0^\infty {\left[ {\sum\limits_{j = 1}^{4N} {Y_i^2 + {\rho ^2}{{\boldsymbol{\beta}} ^2}} } \right]} {\rm{d}}t < \gamma {\left\| \omega \right\|_2}$ | (16) |
所以,使得闭环系统内部稳定的且满足式(16)的H∞控制器则正好是满足控制目标设计(14)的控制器
LMI不等式(12)的求解是一个复杂的问题,这是一个线性矩阵不等式约束的最优化问题,可以采用MATLAB的YALMIP工具箱简化求解过程,在选定鲁棒控制参数
为降低全状态反馈时状态变量检测的误差影响,提出了一种利用状态重构和状态观察器来改善系统性能的思路。由于本挥舞/扭转耦合系统的能观性矩阵始终满秩,故可以设置系统观察器。基于状态观察器的状态重构方案如图3所示。
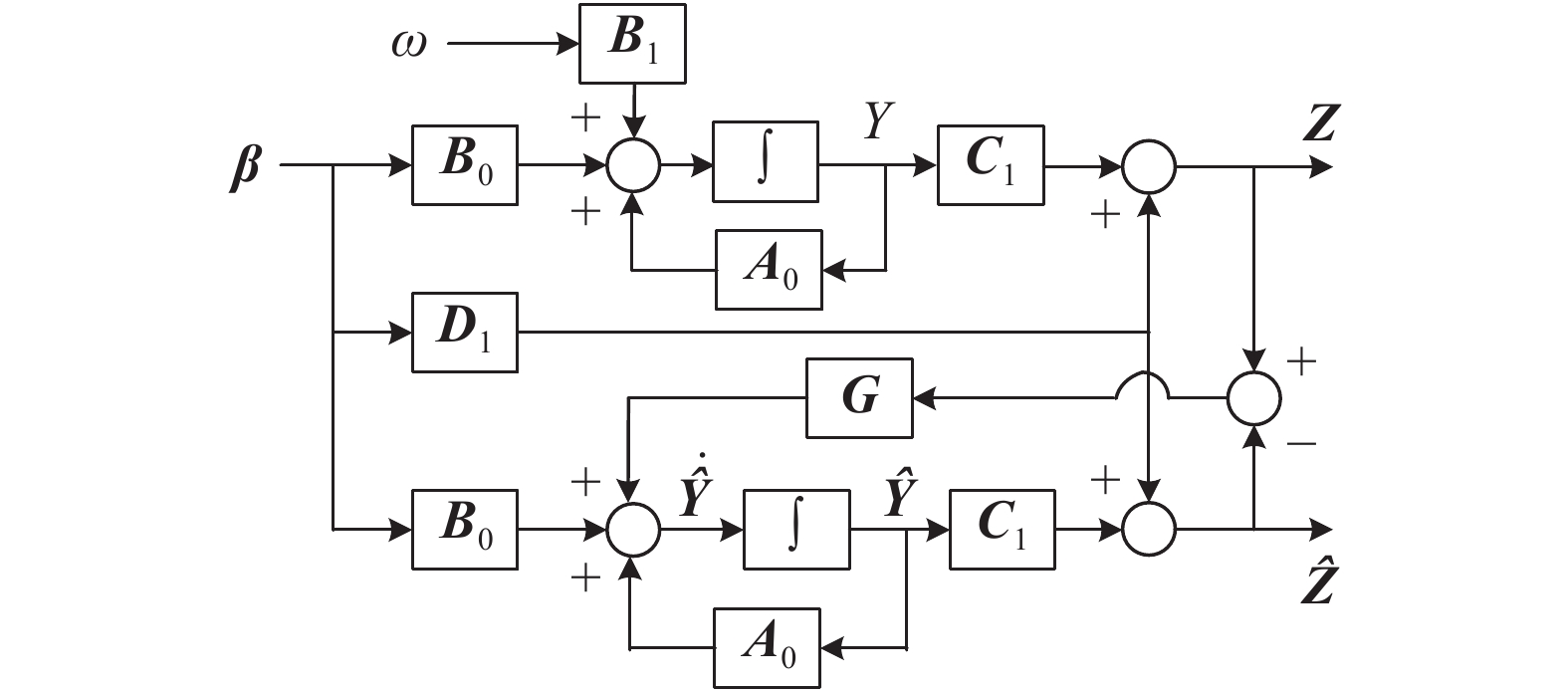 |
| 图3 基于状态观察器的状态重构方案 Fig. 3 State reconstructing scheme based on state observer |
图3中,观察器增益为
| ${\;\;\;\;\;\;\;\;\;\;\;\left\| {\hat {\boldsymbol{Z}}} \right\|_2^2 = \int_0^\infty {\left[ {\sum\limits_{j = 1}^{4N} {\hat {\boldsymbol{Y}}_i^2 + {\rho ^2}{\beta ^2}} } \right]} {\rm{d}}t < \gamma {\left\| \omega \right\|_2}}$ | (17) |
从而使得
图4为无控制情况下的挥舞/扭转位移。由图4可以看出两个位移均处“低幅–高频”振动状态。虽然对于扭转位移而言,振动频率更高,但其幅度数量级非常小(
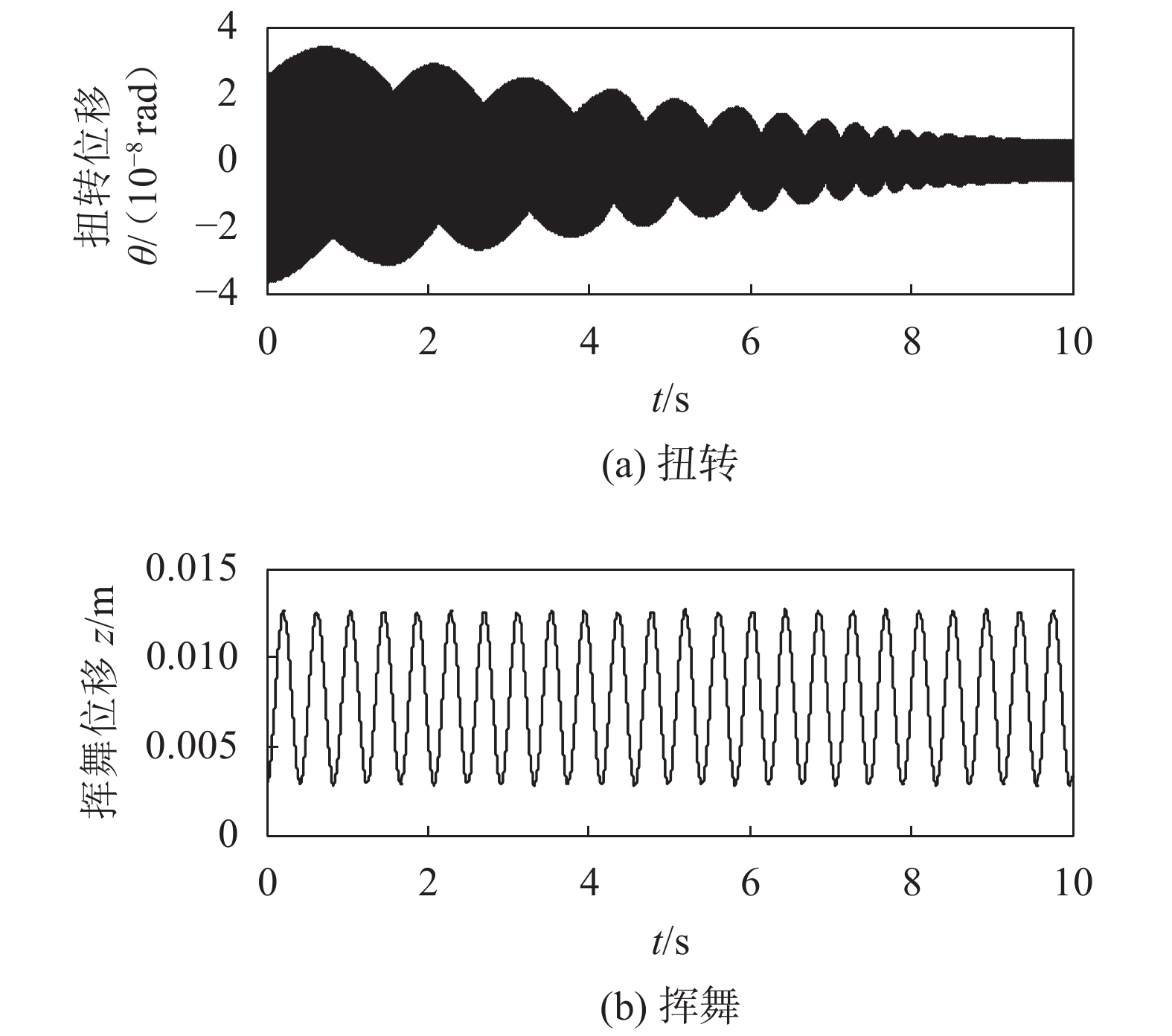 |
| 图4 无控制的挥舞/扭转高频振动位移 Fig. 4 Flap-wise/twist displacements of high frequency vibration without control |
针对图4中的高频振动案例,取鲁棒控制参数
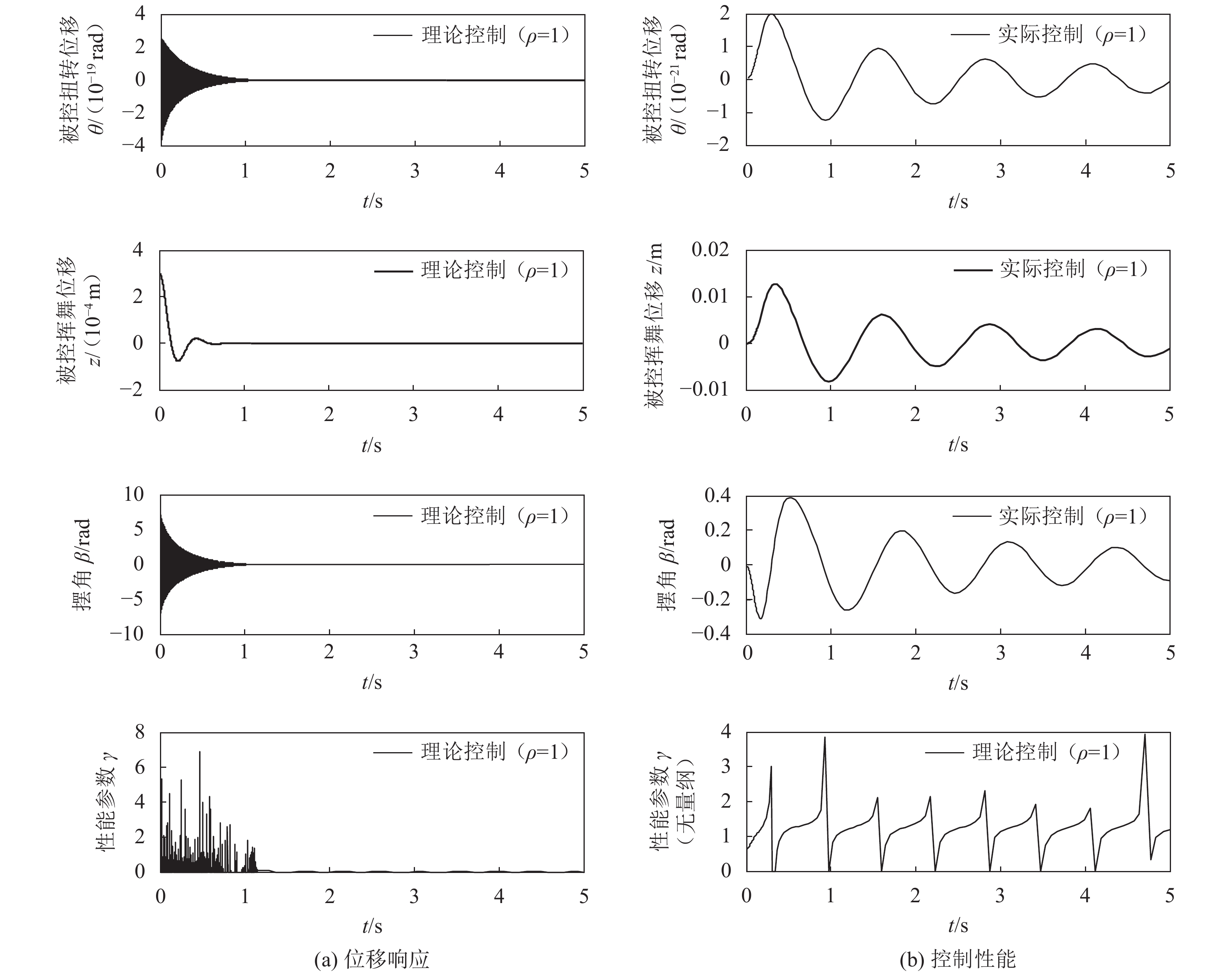 |
| 图5 H∞ 控制下的位移响应以及控制性能 Fig. 5 Displacement responses and control performance under H∞ controller |
图5(b)为控制性能对比,包括控制输入信号和鲁棒性能两方面的对比。从控制器输入(襟翼摆角
鲁棒控制参数
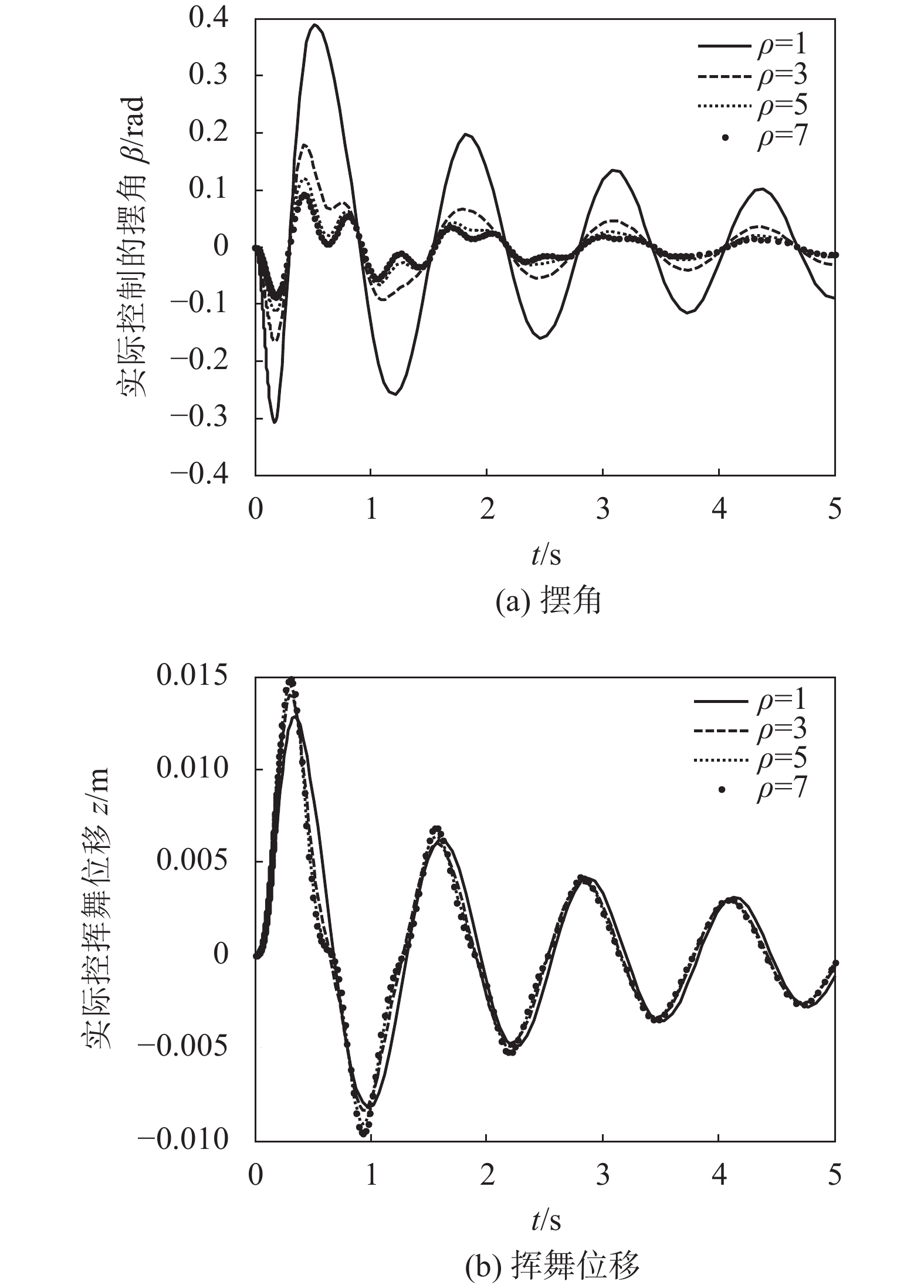 |
|
图6 不同
|
另外,本设计中鲁棒控制参数
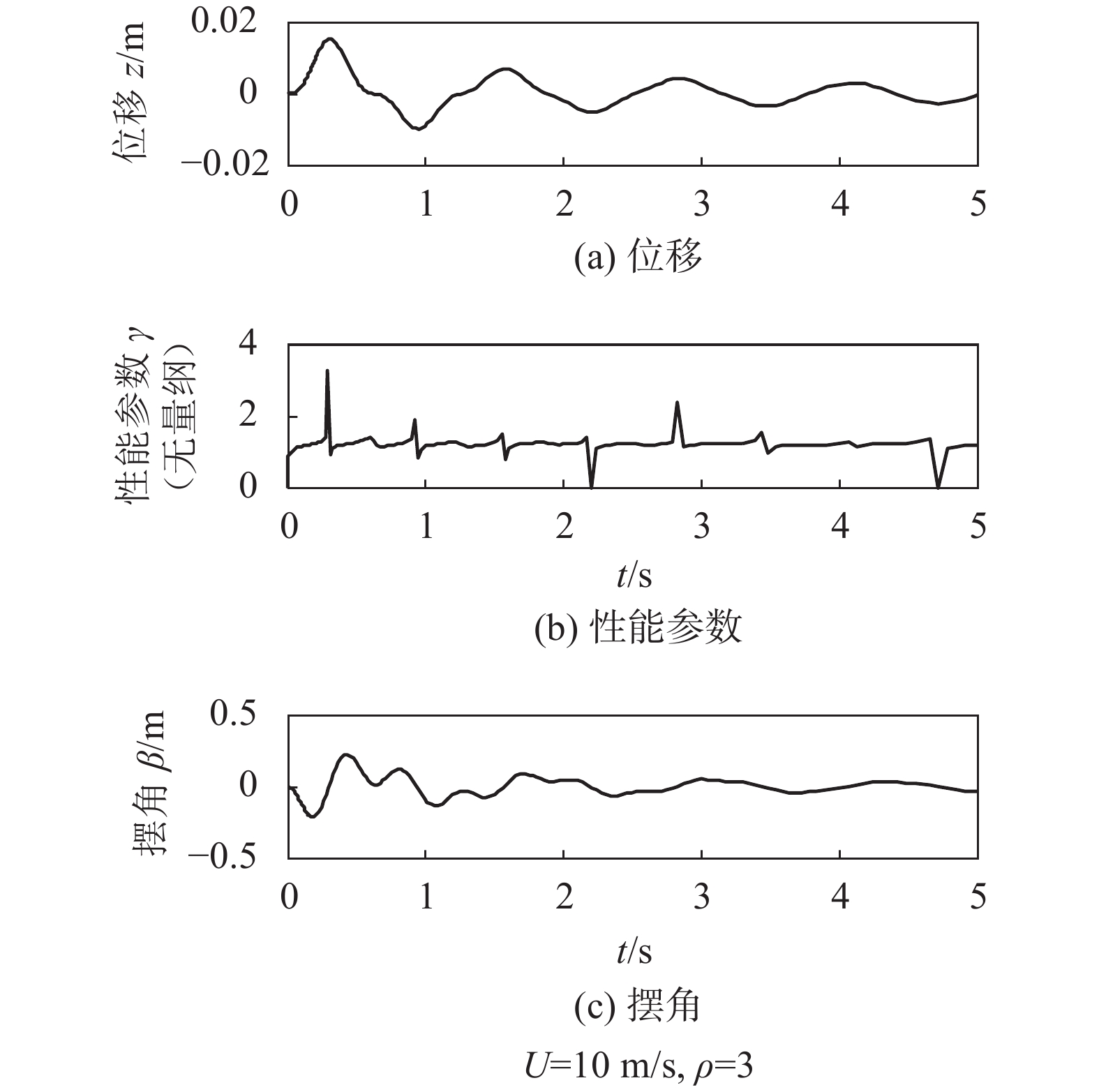 |
|
图7 |
需要说明的是:鉴于改进后的系统方程(11)的控制难度,难以找到适合的其他主动控制方法,故本设计缺少与其他主动控制方案的对比,然而与一些优秀的被动控制方案相比,可以间接论证本方案的有效性。作者所在项目组成员在文献[22]中,研究了基于形状记忆合金(SMA)的被动控制,也能获得较好的幅度控制结果;随着SMA在复合材料母体中的含量的增加,幅度控制效果甚至更加显著,但无论何种情况,基于SMA的被动控制的时域响应时间会延长,此为不利因素。故相对于本文的主动控制,其效果在伯仲之间。
4 基于工程应用的过程控制实验由于常规工控设备的控制器(如PLC)CPU主频和内存等性能的局限、控制器独立程序编制的难度,大多数高性能的智能控制控制算法无法直接在控制器硬件中实现,因此存在着工程应用的局限。OPC技术是一种能把MATLAB/SIMULINK (MS) 仿真环境与PLC连接起来实时数据通信的技术[23-24]。为检验过程控制性能,即检验本文提出的H∞控制算法在实际的控制器硬件系统中的有效性、实时性和可靠性,本设计采用基于S7–300PLC、WinCC组态软件、MS 环境的“实时OPC技术”来实现基于硬件的控制算法工程应用、数据通讯、虚拟仿真技术。
常规的OPC技术仅仅实现MS仿真环境和S7–300PLC的数据通讯功能,实时OPC技术能将智能控制算法在控制器硬件中完美实现,能将基于SIMULINK构架的算法程序转换为PLC控制器程序,从而实现与仿真环境的联机通讯和算法的执行。具体步骤如下:1)采用Simulink® PLC CoderTM工具,将嵌入SIMULINK的MATLAB代码(以S-function形式嵌入)作为一个整体,直接编译成与硬件无关的IEC 61131结构化文本(ST);2)以ST形式生成的代码具有专业手写代码的清晰性和高效性。在此基础上作适当修改,修改为适合于S7–300PLC运行的“新ST”文本;3)将新ST文本编译并部署到S7–300PLC上直接应用,或者转化成梯形图程序后再应用;4)由于PLC扫描周期的限制,如果扫描周期过长,则可以启动冗余控制器系统来分部运行控制算法。5)H∞控制理论完全在S7–300控制器硬件中运行;叶片系统的虚拟仿真过程完全在MS环境实现;WinCC作为OPC服务器,一方面与客户端S7–300通讯,另一方面与客户端MS环境的叶片系统模型通讯。MS中的OPC toolbox模块库,具有相关的OPC读写模块,借助于OPC服务器,可实现与S7–300的读写操作。
以图5中鲁棒控制参数
 |
| 图8 控制柜系统及过程控制性能检验 Fig. 8 Controller hardware system and performance test for process control |
5 结 论
1)高频振动分析是建立在92%展长分布的尾缘襟翼驱动的实心CAS铺层的旋转复合材料叶片梁的基础上;气动力是基于一种新颖的、适合于襟翼结构的准稳态气动力模型。气弹方程离散化通过Galerkin方法实现,并通过对比验证了该方法的有效性。
2)分别基于理论H∞控制和实际H∞控制实现了低幅–高频振动的控制,实际控制基于步进电机驱动。H∞控制基于LMI设计,基于YALMIP工具箱的LMI求解可以简化计算,基于状态观察器的状态重构方案获得了良好的鲁棒性能。
3)探讨了H∞控制算法中鲁棒控制参数取值的影响,为同类H∞控制提供了依据;同时也描述了不同鲁棒控制参数下襟翼结构的步进电机驱动效应,且鲁棒性能稳定,为叶片襟翼结构的物理实现和系统控制驱动提供了可行性方案。
4)基于实时OPC技术实现了本文提出的H∞控制算法的过程控制性能检验。保证了控制算法在实际的控制器硬件系统中的有效性、实时性和可靠性,也为其它高性能智能控制算法的工程应用提供了可行性方案。
| [1] |
Li Nailu,Balas M J,Nikoueeyan P,et al. Stall flutter control of a smart blade section undergoing asymmetric limit oscillations[J]. Shock and Vibration, 2016, 2: 1-14. DOI:DOI:10.1155/2016/5096128 |
| [2] |
Hayat K,de Lecea A G M,Moriones C D,et al. Flutter performance of bend–twist coupled large-scale wind turbine blades[J]. Journal of Sound and Vibration, 2016, 370: 149-162. DOI:10.1016/j.jsv.2016.01.032 |
| [3] |
Haselbach P U. An advanced structural trailing edge modelling method for wind turbine blades[J]. Composite Structures, 2017, 180: 521-530. DOI:10.1016/j.compstruct.2017.08.029 |
| [4] |
Llorente E,Ragni D. Trailing-edge serrations effect on the performance of a wind turbine[J]. Renewable Energy, 2020, 147: 437-446. DOI:10.1016/j.renene.2019.08.128 |
| [5] |
Chen Hao,Qin Ning. Trailing-edge flow control for wind turbine performance and load control[J]. Renewable Energy, 2017, 105: 419-435. DOI:10.1016/j.renene.2016.12.073 |
| [6] |
Zhang Wenguang,Bai Xuejian. Modeling of a smart blade wind turbine and its multi-target control with trailing edge flaps[J]. Journal of Chinese Society of Power Engineering, 2018, 38(4): 321-328. [张文广,白雪剑. 智能叶片风力机建模及多目标尾缘襟翼控制[J]. 动力工程学报, 2018, 38(4): 321-328. DOI:10.3969/j.issn.1674-7607.2018.04.011] |
| [7] |
Zhang Guangxing.The active flow control of high-aspect-ratio wind turbine blade based on trailing-edge flaps[D].Xi’an:Xi’an University of Technology,2017. 张广兴.基于尾缘襟翼的大展弦比风力机桨叶的主动流动控制[D].西安:西安理工大学,2017. |
| [8] |
Mu Anle,Zhang Guangxing,Li Nailu,et al. Modal predictive flow control of wind turbine blades based on distribured flaps[J]. Journal of Vibration and Shock, 2018, 37(14): 79-85. [穆安乐,张广兴,李迺璐,等. 基于分布式襟翼风力机桨叶的模型预测振动控制[J]. 振动与冲击, 2018, 37(14): 79-85.] |
| [9] |
Bolin K,Bluhm G,Eriksson G,et al. Infrasound and low frequency noise from wind turbines:Exposure and health effects[J]. Environmental Research Letters, 2011, 6(3): 035103. DOI:10.1088/1748-9326/6/3/035103 |
| [10] |
Jianu O,Rosen M A,Naterer G. Noise pollution prevention in wind turbines:Status and recent advances[J]. Sustainability, 2012, 4(6): 1104-1117. DOI:10.3390/su4061104 |
| [11] |
Liu Xiong,Lu Cheng,Liang Shi,et al. Vibration-induced aerodynamic loads on large horizontal axis wind turbine blades[J]. Applied Energy, 2017, 185(2): 1109-1119. |
| [12] |
Zuheir S,Abdullah O I,Al–Maliki M. Stress and vibration analyses of the wind turbine blade[J]. Journal of Mechanical Engineering Research and Developments, 2019, 42(4): 14-19. DOI:10.26480/jmerd.04.2019.14.19 |
| [13] |
Wang Xudong,Chen Jin,Shen Wenzhong,et al. Integration study on airfoil profile for wind turbines[J]. China Mechanical Engineering, 2009, 20(2): 211-213. [王旭东,陈进,Shen Wenzhong,等. 风力机叶片翼型型线集成设计理论研究[J]. 中国机械工程, 2009, 20(2): 211-213. DOI:10.3321/j.issn:1004-132X.2009.02.020] |
| [14] |
Liu Tingrui,Ren Yongsheng. Nonlinear aeroelastic response analysis of rotor blade modeled as composite thin-walled structure[J]. Acta Energiae Solaris Sinica, 2012, 33(1): 105-112. [刘廷瑞,任勇生. 基于复合材料薄壁结构的转子叶片非线性气弹时域响应分析[J]. 太阳能学报, 2012, 33(1): 105-112. DOI:10.3969/j.issn.0254-0096.2012.01.018] |
| [15] |
Singh S N,Yim W. State feedback control of an aeroelastic system with structural nonlinearity[J]. Aerospace Science and Technology, 2003, 7(1): 23-31. DOI:10.1016/S1270-9638(02)00004-4 |
| [16] |
Hodges D H,Pierce G A.Introduction to structural dynamics and aeroelasticity[M].Cambrige:Cambrige University Press,2002,55–75.
|
| [17] |
Stefan Dancila D,Armanios E A. The influence of coupling on the free vibration of anisotropic thin-walled closed-section beams[J]. International Journal of Solid and Structures, 1998, 35(23): 3105-3119. DOI:10.1016/S0020-7683(97)00365-X |
| [18] |
刘金琨.机器人控制系统的设计与MATLAB仿真:先进设计方法[M].北京:清华大学出版社.2017.
|
| [19] |
龚仲华.S7–200/300/400 PLC应用技术——提高篇[M].北京:人民邮电出版社.2012.
|
| [20] |
Yu Ziqing.Numerical simulation of free vibration of piezoelectric composite cantilever blade[D].Qingdao:Shandong University of Science & Technology,2016. 于子晴.压电复合材料悬臂叶片自由振动数值模拟[D].青岛:山东科技大学,2016. |
| [21] |
Yuan Quanyong,Li Chun,Yang Yang,et al. Research on comparison of the fractal characteristics of turbulent wind[J]. Acta Energiae Solaris Sinica, 2018, 39(7): 2027-2035. [袁全勇,李春,杨阳,等. 湍流风分形特性对比研究[J]. 太阳能学报, 2018, 39(7): 2027-2035.] |
| [22] |
刘廷瑞.风力机叶片动力失速气弹稳定性分析及颤振抑制[M].里加:金琅学术出版社.2017.
|
| [23] |
Liu Tingrui. Flutter suppression of blade section based on model prediction control[J]. Transactions of the Institute of Measurement and Control, 2020, 42(9): 1-13. |
| [24] |
Zhang Lieping,Zeng Aiqun,Zhang Yunsheng.On remote real-time communication between MATLAB and PLC based on OPC technology[C]//Proceedings of the 26th Chinese Control Conference.Zhangjiajie:IEEE,2007,544–548.
|
 2021, Vol. 53
2021, Vol. 53

