System Transformation Scheme of Self-anchored Suspension Bridge of Non-extension Suspender Cables and Numerical Simulation of Cable Saddle
-
摘要: 为降低自锚式悬索桥体系转换施工费用、提高施工效率、简化分析过程，以抛物线理论为依据，推导出主缆垂度的影响参数，结合各参数的可控性、敏感性，通过调整主索鞍顶推和吊杆张拉策略，提出3阶段2轮张拉吊索不接长体系转换方案。为在有限元计算时精确模拟方案中主、散索鞍施工状态，将索鞍圆心点与塔顶或散索鞍底座中心点建立刚臂和主从约束两个边界，通过激活、钝化刚臂模拟索鞍临时固定和滑移状态，通过设置索鞍圆心点强制位移模拟索鞍超顶状态。以双塔3跨和独塔2跨2座自锚式悬索桥为例，根据现场实际情况分别制定了2套吊索不接长体系转换方案，并建立有限元模型对2座桥梁体系转换过程进行模拟和分析。结果表明：自锚式悬索桥主跨是避免吊索接长的关键桥跨，主缆跨径和主缆长度是影响主缆垂度、避免吊索接长的关键可控参数；通过增大主缆初期变形可有效避免吊索接长，实施方案为张拉主跨长出段吊索使主索鞍超前就位，以改变主缆跨度；提前施工部分二期恒载、加劲梁在第1轮吊索张拉后脱架，以增加主缆弹性伸长。由2座桥梁实例分析结果可知，体系转换前期主索鞍可控滑移、超前就位，后期对称张拉桥塔两侧吊索，使主缆和主索鞍间的抗滑移安全系数和桥塔应力均变化平稳，所提方案和索鞍模拟方法达到了预期目的，可为同类型自锚式悬索桥体系转换提供参考。Abstract: To reduce the construction cost, improve the construction efficiency and simplify the analysis process of system transformation of a self-anchored suspension bridge, the influencing parameters of the main cable sag were derived based on the parabola theory, and by adjusting the cable saddle pushing and suspender cable tensioning strategies, a three-stage and two-round system transformation theme of non-extension suspender cables in combination with the controllability and sensitivity of each parameter was proposed. To simulate the construction status of the main and splay cable saddles in the scheme in the finite element calculation, the center point of the cable saddle and the tower top point or the center point of the splay cable saddle base were used to establish two boundaries, namely, the rigid arm and the principal and subordinate constraints. The temporary fixing and sliding status of the cable saddle were simulated by activating and deactivating the rigid arm, and the over-pushing status of the cable saddle was simulated by setting the forced displacement of the cable saddle center point. Taking two examples with a two-tower-three-span bridge and a single-tower-two-span bridge, according to the actual situation of the site, two sets of system transformation schemes of non-extension suspender cables were formulated respectively, and the FEM was established to simulate and analyze the system transformation process of the two bridges. The results of parameter analysis showed that the main span of the self-anchored suspension bridge was the key span to avoid the extension suspender cables, and the main cable span and main cable length were the key controllable parameters that affect the sag of main cables and avoid the extension suspender cables. The extension suspender cables can be effectively avoided by increasing the initial deformation of the main cable. The construction scheme was to change the span of the main cable by tensioning suspender cables to the main span longer segments to make the cable saddles reach the designated position in advance, and to increase the elastic elongation of the main cable by pouring the part of the secondary dead load and tensioning suspender cables in the first round to make the stiffening beam leave from the scaffold. The analysis results of two bridge examples showed that in the early stage of the system transformation, the main cable saddles were in the controllable slip state and the designated position in advance, and in the later period, the suspender cables on both sides of the tower were tensioned symmetrically, so that the anti-slip safety factor and the bridge tower stress changed steadily, and the establishing process of the scheme was simplified. The proposed scheme cable saddle simulation method has achieved the expected purpose, which can provide a reference for the system transformation of self-anchored suspension bridges of the same type.
-
自锚式悬索桥主要采用先梁后缆的施工方法，在施工中通过张拉吊索，使加劲梁由临时支架支撑转换至缆索系统支撑；通过顶推主索鞍，平衡主索鞍两侧主缆水平分力，使桥塔处于安全状态[1-2]。在已建成的自锚式悬索桥中，有双塔3跨自锚式悬索桥，如：黄河桃花峪大桥采用主跨和边跨吊索均从桥塔开始向跨中或者散索鞍侧张拉，主索鞍分3次顶推[3]；扬州万福大桥采用吊索从塔根向跨中张拉，中跨中部吊索采用多次循环张拉，并对主梁进行临时压重[4]。有独塔2跨自锚式悬索桥，如：猎德大桥采用主跨先长索后短索，边跨吊索交替张拉、先中索再短索、长索，以吊索无应力索长控制张拉[5]；福州鼓山大桥采用主跨与边跨吊索交替张拉，主、边跨吊索先由桥塔向锚跨张拉，之后边跨剩余7对吊索由锚跨向桥塔张拉[6]。以上各种桥梁均安全、顺利地完成了结构的体系转换。学者和工程师们同时也对自锚式悬索桥的体系转换原则[3,5]、吊索张拉顺序[3-6]、计算分析方法[7-8]、施工中的临时措施[4]、受力特点[9-10]、索力和主缆线形变化规律[11-12]等方面进行了深入的研究。但在施工过程中，以上桥梁均需制作接长杆件，对吊索进行临时接长，此举增加了施工费用并且影响施工效率。
在主索鞍顶推控制方面，齐东春等[13]提出了主索鞍平衡条件的合理模式，指出顶推量和时间主要由塔底应力及主缆抗滑移安全系数控制。在已有的自锚式悬索桥体系转换方案中，主索鞍顶推也均按此原则，将索鞍顶推作为配合吊索张拉的手段，根据不同的吊索张拉顺序和张拉力，伺机对主索鞍进行顶推[3-6]。在施工过程中，何为等[14]提出“小步快跑”原则，即对主索鞍采取多次少量的顶推控制方法；孙胜江等[15]提出主索鞍“可控状态自由滑移”的控制方法，即主索鞍在梁体施工过程中可以自由滑动。以上控制方法均将注意力集中在通过顶推主索鞍来改善桥塔受力，而对主索鞍顶推后改变主缆跨度，进而改变主缆垂度这一现象没有深入的研究。在数值仿真计算方面，张海顺等[16]提出采用降温法对主索鞍顶推过程进行模拟；路韡等[17]提出在体系转换过程中，滑动式散索鞍滑移边界的处理会对成桥吊索力产生明显的影响。因此，为制定吊索不接长的体系转换方案，需重新考虑主索鞍顶推策略，并建立精确的主、散索鞍顶推、滑移模型。
本文首先提出自锚式悬索桥吊索不接长的原理，以悬索桥主缆线形抛物线理论为依据，推导出主缆线形由空缆状态至成桥状态变化的影响参数，结合各参数的可控性和敏感性，调整主索鞍顶推和吊杆张拉策略，提出自锚式悬索桥吊索不接长体系转换方案。然后，结合主索鞍和滑动式散索鞍在施工中的状态，讨论了主、散索鞍的数值模拟方法。最后，以双塔3跨和独塔2跨2座自锚式悬索桥为例，证明该体系转换方案和主、散索鞍模拟方法的可行性。
1. 吊索不接长体系转换方案
在体系转换过程中，伴随吊索的逐对、逐轮张拉，主缆会发生显著的几何非线性变形，由空缆状态逐渐到达成桥状态，加劲梁被吊索逐渐提离临时支架[18]。在此过程中吊索是否接长，要看主缆与加劲梁对应吊点位置之间的距离是否超出吊索可调节范围，若主缆变形充分，线形接近成桥状，则可以减小甚至避免吊索接长。本文提出的吊索不接长方案的基本原理是在自锚式悬索桥体系转换过程的初期尽可能通过合理的施工工序增大主跨主缆变形，使吊索在首轮安装、张拉工况不采用临时接长，就能够锚固在加劲梁上。由于主缆变形量远大于加劲梁，因此体系转换过程中主缆线形是控制吊索是否接长的重要参数。分段悬链线法[19-20]能够根据各吊索索力和各段吊索间主缆无应力长度精确计算出施工各阶段的主缆线形，但缆索布置形式在不同桥跨结构中各不相同，该理论不便于揭示主缆线形变化的一般规律。考虑到自锚式悬索桥主跨跨度普遍在400 m以下[21]，主缆跨中垂度是主缆线形重要的控制参数[18]，主缆线形可采用抛物线理论对主缆垂度进行分析。
1.1 抛物线理论的主缆长度
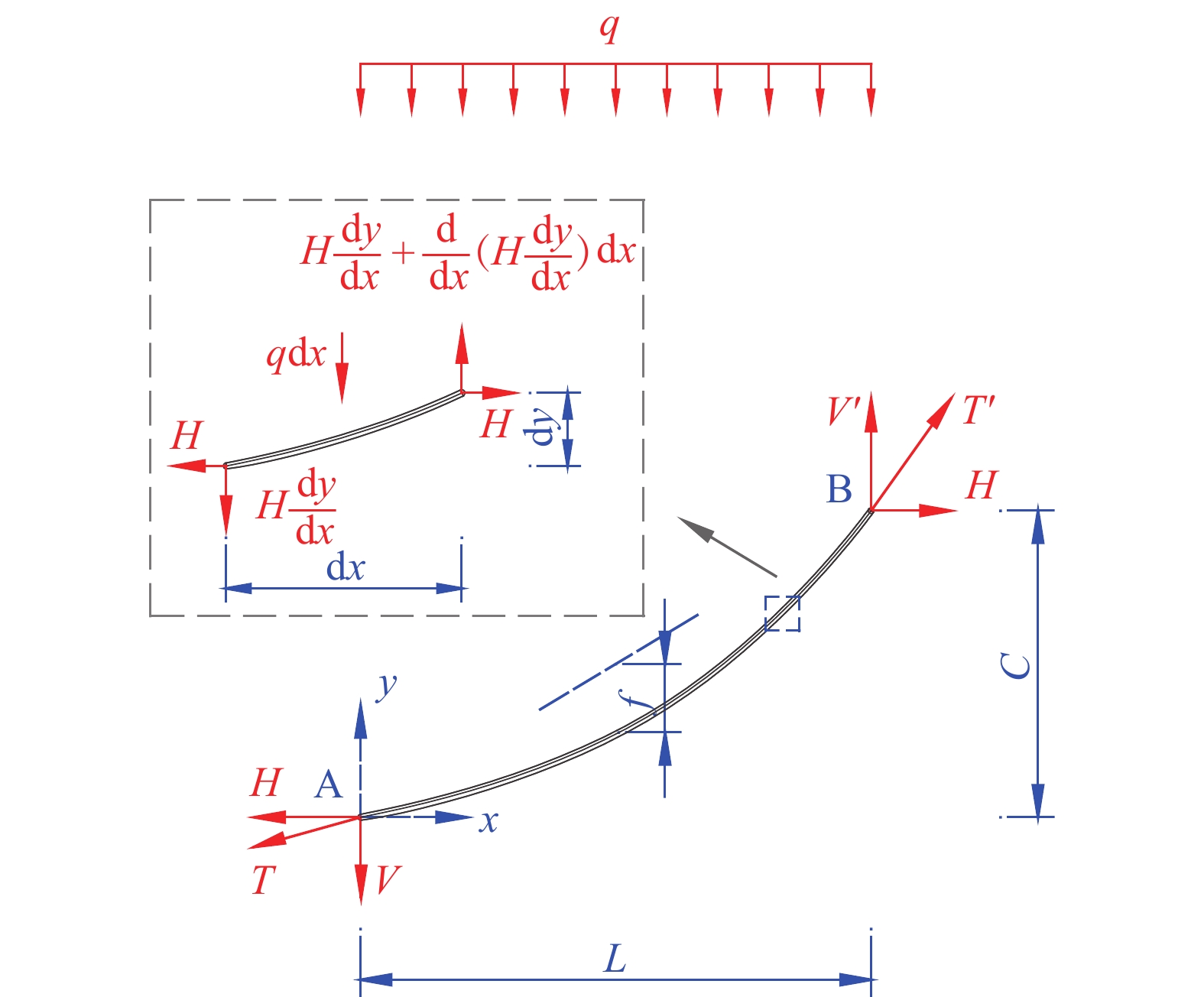
抛物线理论中，假定主缆自重较梁体自重小，且所有恒载简化为沿跨度均布[22-23]；不考虑主缆弹性伸长对均布荷载的影响，其主缆线形计算如图1所示。图1中：A、B两点之间为一段主缆，设在跨径L内的均布荷载为q；跨中垂度为f；高差为C；抗拉刚度为EA，其中，E为主缆弹性模量，A为主缆面积；T、T'分别为A、B两点主缆拉力；V、V'分别为A、B两点的竖向分力；H为主缆的水平分力。
图 1 抛物线理论下主缆线形计算图Fig. 1 Main cable shape calculation diagram under parabolic theory
下载:
全尺寸图片
对主缆取微元，在竖向建立平衡方程得：
$$ \frac{{\text{d}}}{{{\text{d}}x}}\left(H\frac{{{\text{d}}y}}{{{\text{d}}x}}\right) - q = 0 $$ (1) 对式（1）进行二次积分，并代入A、B两点边界条件(0,0)、(L,C)得：
$$ y = - \frac{{qx}}{{2H}}(L - x) + \frac{C}{L}x $$ (2) 代入跨中几何条件
$\left(\dfrac{L}{2},\dfrac{C}{2} - f\right)$ 得：$$ y = - \frac{{4fx}}{{{L^2}}}(L - x) + \frac{C}{L}x $$ (3) 由于主缆微元长度为：
$$\qquad\qquad {\text{d}}s = \sqrt {{{({\text{d}}x)}^2} + {{({\text{d}}y)}^2}} = \sqrt {1 + {{\left(\frac{{{\text{d}}y}}{{{\text{d}}x}}\right)}^2}} {\text{d}}x $$ (4) 故主缆长度为：
$$ S = {\int_{\text{0}}^L {\left[1 + {{\left(\frac{{{\text{d}}y}}{{{\text{d}}x}}\right)}^2}\right]} ^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}{\text{d}}x = \frac{{{L^2}}}{{16f}}\left[ {{D_1}{D_3} - {D_2}{D_4} + {D_5}} \right] $$ (5) 式中，
$ {D_1} = \dfrac{{C + 4f}}{L} $ ，$ {D_2} = \dfrac{{C - 4f}}{L} $ ，$ {D_3} = \sqrt {1 + D_1^2} $ ，${D_4} = \sqrt {1 + D_2^2}$ ，$ {D_5} = \ln \dfrac{{{D_1} + {D_3}}}{{{D_2} + {D_4}}} $ 。主缆弹性伸长
$\Delta S $ 和水平分力$H $ 分别为：$$ \qquad\qquad \Delta S = \;\int {\frac{{T{\text{d}}s}}{{EA}}} = \;\int_0^x {\frac{{H{{{\text{d}}s} \mathord{\left/ {\vphantom {{{\text{d}}s} {{\text{d}}x}}} \right. } {{\text{d}}x}}}}{{EA}}} {\text{d}}x = \frac{{HS}}{{EA}} $$ (6) 式中：H为主缆水平分力，
$H = \dfrac{{q{L^2}}}{{8f}} $ ；S为主缆长度。1.2 主缆垂度的影响参数
由式（5）可知，f 仅与L、S和C 3个参数相关。在主缆由空缆状态变化到成桥状态的过程中，由于索鞍在主缆架设时设置预偏，L会在该过程中发生变化。由于主缆在空缆状态下仅承受主缆自重（
$ {q}_{空} $ ）的作用，而在成桥状态下还需承受加劲梁自重（$ {q}_{梁} $ ）和二期恒载（$ {q}_{二} $ ）作用，S会在该过程中变长。除此之外，梁体压缩和桥塔压缩也会分别改变L和C，但压缩量相对主缆伸长量和主索鞍预偏量通常会小一个数量级以上，且属于被动参数不能在体系转换过程中参与主动控制，故在下文方案制定中不再考虑。现将式（5）中
$ f $ 看作是S和L的函数，并分别对其求偏导数，可得式（8）、（9）：$$ {\qquad\quad\;\;\frac{{{\text{d}}f}}{{{\text{d}}S}} = \frac{{16n_{\text{f}}^2}}{{{D_2}{D_4} - {D_1}{D_3} - {D_5}{\text{ + }}{D_6}}}} $$ (7) $$\qquad\qquad \frac{{{\text{d}}f}}{{{\text{d}}L}} = \frac{{2{n_{\text{f}}}{D_5}}}{{{n_{\text{c}}}({D_3} - {D_4}) - 4{n_{\text{f}}}({D_3} + {D_4}) + {D_5}}} $$ (8) 式中，
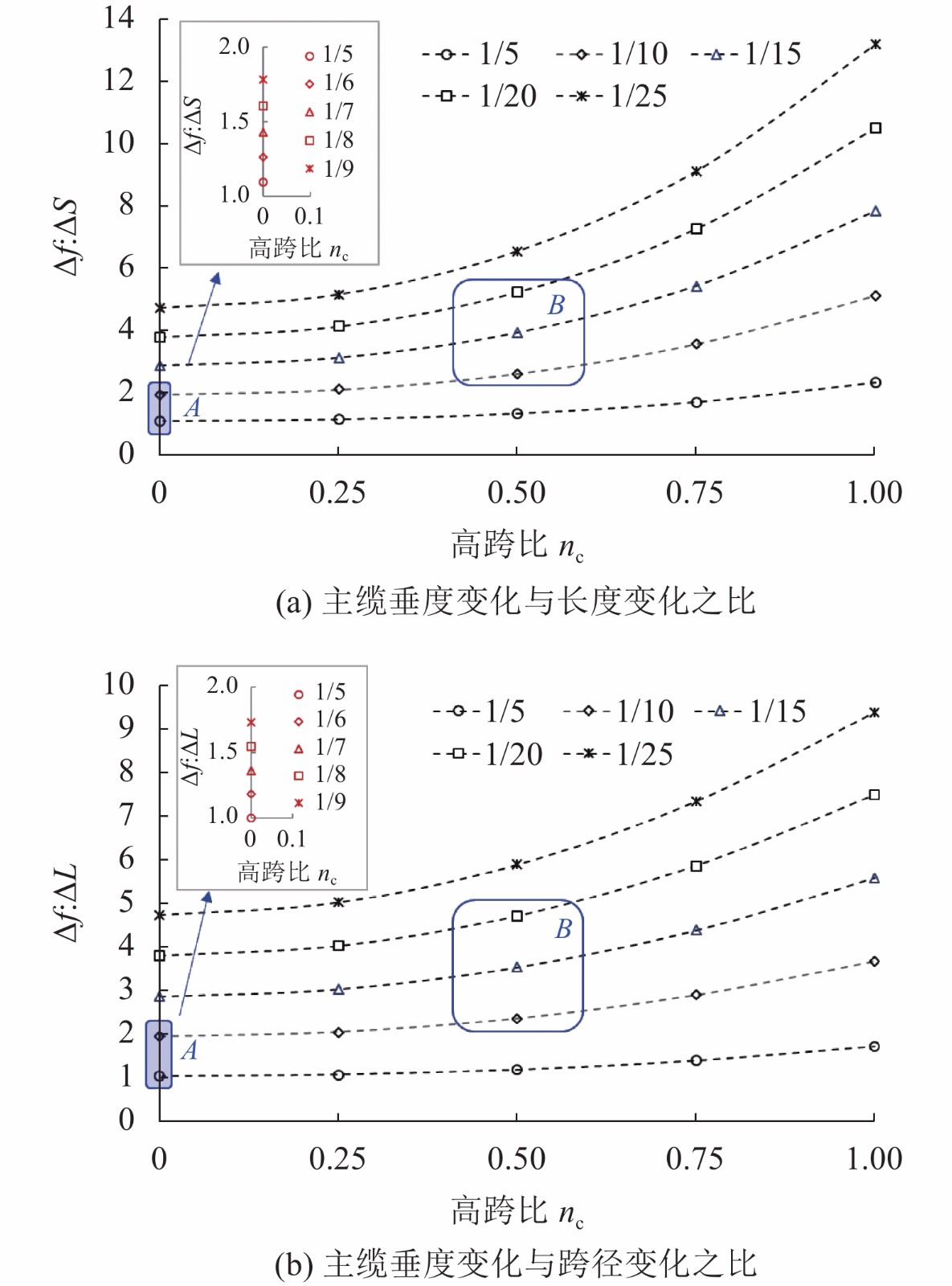
$ {D_6}{\text{ = }}4{n_{\text{f}}}\left[ {({D_3} + {D_4})(1 + \dfrac{1}{{{D_3}{D_4}}}) + \dfrac{{D_1^2}}{{{D_3}}} + \dfrac{{D_2^2}}{{{D_4}}}} \right] $ ，$ n_{{\text{ f}}}^{}{\text{ = }}\dfrac{f}{L} $ ，$ n_{\text{c}}^{}{\text{ = }}\dfrac{C}{L} $ 。选取不同矢跨比（
$ n_{\text{f}}^{} $ ）和高跨比（$ n_{\text{c}}^{} $ ）值分别代入式（8）、（9），可得主缆垂度变化和主缆长度变化之比（Δf /ΔS）与主缆垂度变化和跨径变化之比（Δf /ΔL）,如图2所示。图2中，根据中国已建桥梁数据[21]可知，双塔3跨自锚式悬索桥中跨$ n_{\text{f}}^{} $ 主要在1/9～1/5，若两主塔等高，则$ n_{\text{c}}^{} $ 为0，则Δf /ΔS和Δf /ΔL集中于区域A。双塔3跨自锚式悬索桥的边跨$ n_{\text{f}}^{} $ 和独塔2跨自锚式悬索桥主、边跨$ n_{\text{f}}^{} $ 主要在1/20～1/10，$ n_{\text{c}}^{} $ 主要在0.4～0.6，则Δf /ΔS和Δf /ΔL集中于区域B。
图 2 不同矢跨比和高跨比变化下主缆垂度变化与主缆长度和跨径变化之比Fig. 2 Variation curves of ratio of the sag variation to length and span variation of main cable under different sag-span ratio and high-span ratio下载:
全尺寸图片
由图2可知：
1）主缆长度增长，主缆垂度增大，主缆长度变化与主缆垂度变化呈正相关；矢跨比越小，主缆长度变化对主缆垂度影响越显著。在体系转换过程中，随着梁体自重逐渐由主缆承担，主缆会弹性伸长，垂度也会逐渐增大。在区域A，当矢跨比为1/5和1/9时，Δf/ΔS分别为1.10和1.78；在区域B该变化更为显著，当矢跨比
$ n_{\text{f}}^{} $ 为1/15、$ n_{\text{c}}^{} $ 为0.5时，Δf /ΔS为3.9。2）主缆跨径增大，主缆垂度减小，主缆跨径变化与主缆垂度变化呈负相关；矢跨比越小，主缆跨径变化对主缆垂度影响越显著。在体系转换过程中，随着主索鞍逐渐向主跨方向顶推，使得主跨跨径减小，边跨跨径增大，进而使主跨垂度增大，边跨垂度减小。在区域A，当
$ n_{\text{f}}^{} $ 为1/5和1/9时，Δf /ΔL分别为1.00和1.91；在区域B，该变化更为显著，当$ n_{\text{f}}^{} $ 为1/15、$ n_{\text{c}}^{} $ 为0.5时，Δf/ΔL为3.5。由以上分析可知：伴随主缆弹性伸长和主索鞍顶推，主跨主缆垂度会显著增大；而在主缆变长、跨度变大，一正一负2个参数作用下，边跨主缆垂度则变化较小。因此，在体系转换过程中自锚式悬索桥主跨是避免吊索接长的关键桥跨，主缆跨径和主缆长度是影响主缆垂度的关键可控参数。
对已建桥梁体系转换方案[3-6]分析可知：由于主索鞍不能尽早到达成桥位置，使主缆不能充分变形，是造成吊索接长的主要原因；在加劲梁脱架后，二期恒载施工使主缆不能尽早充分伸长，是造成吊索接长、支座易出现负反力的重要原因。
1.3 体系转换方案
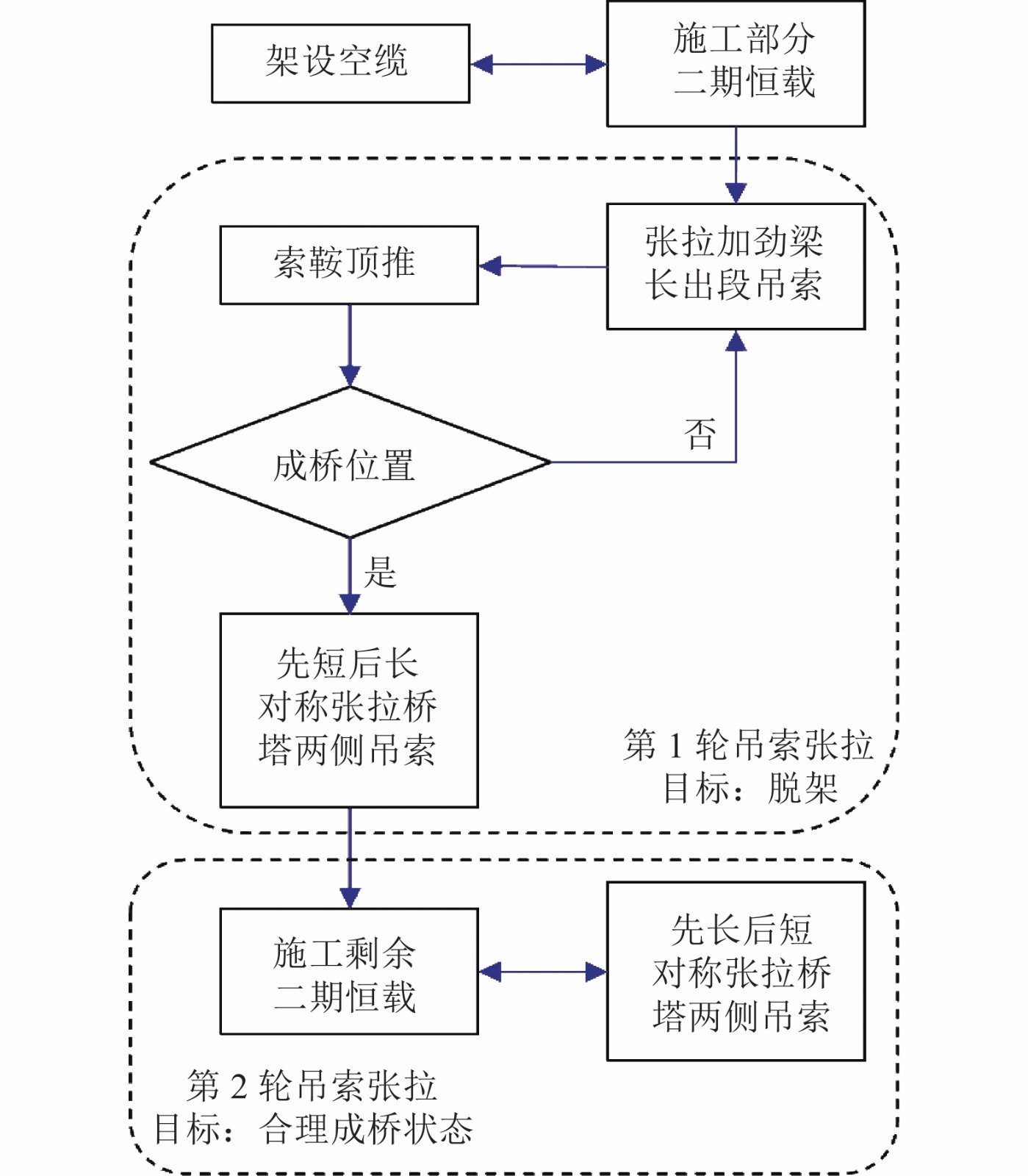
为在体系转换过程中不接长吊索，需尽早增加主跨主缆垂度。在吊索张拉初期主索鞍到达成桥位置，即主索鞍超前就位，减小主跨跨径；提前施工部分二期恒载，使加劲梁在吊索第1轮张拉后脱架，增加主缆弹性伸长；吊索张拉变形控制在张拉下限，避免主缆在张拉吊点位置发生过大的几何变形。由此提出3阶段2轮张拉吊索不接长体系转换方案，如图3所示。
图 3 体系转换流程图Fig. 3 System transformation flow chart下载:
全尺寸图片
由图3可知：第1阶段中，部分二期恒载施工可根据实际情况与空缆架设并行交叉施工，以增大第1轮中吊索张拉力，进而增大加劲梁脱架后主缆的弹性伸长，使支座在吊索张拉过程中不易脱空[24]。第2阶段中，通过逐对张拉主跨长出段吊索并配合主索鞍进行滑移顶推，使主索鞍在第1轮吊索张拉前期到达成桥位置，以增大主缆垂度；计算吊索张拉力时，控制吊索竖向位移在成桥位置和张拉控制下限之间，即可避免吊索接长，也避免了对个别吊索超张拉造成主缆在该吊点产生较明显的几何非线性变形，进而造成后续吊索需要接长的情况。第3阶段中，剩余二期恒载施工与第2轮吊索张拉可调整先后顺序，但不建议并行施工。
为判断体系转换方案的可行性，设在加劲梁自重
$ {q}_{梁} $ 和部分二期恒载（$ {{q}^{\prime }} _{二}^{} $ ）作用下主缆的弹性伸长为$ \Delta S' $ ，在A、B两点之间主索鞍和滑移式散索鞍纵向预偏距离之和为$ \Delta L' $ ，可得在第1轮吊索张拉后由主缆弹性伸长和跨径变化引起的主缆垂度变化量$ \Delta f' $ 为：$$ \Delta f' = \Delta S' \cdot \frac{{{\text{d}}f}}{{{\text{d}}S}}{\text{ + }}\Delta L' \cdot \frac{{{\text{d}}f}}{{{\text{d}}L}} $$ (9) 再用
$ \Delta f' $ 与主缆在空缆状态（$ {f}_{空} $ ）和成桥状态（$ {f}_{成} $ ）下垂度的差值（Δ）进行比较，判断Δ是否在吊索调节范围内，即可知吊索是否需要接长。$${\qquad\quad\;\;\varDelta=f_{\text {成 }}-f_{\text {空 }}-\Delta f^{\prime}=\Delta f-\Delta f^{\prime}} $$ (10) 2. 索鞍数值模拟
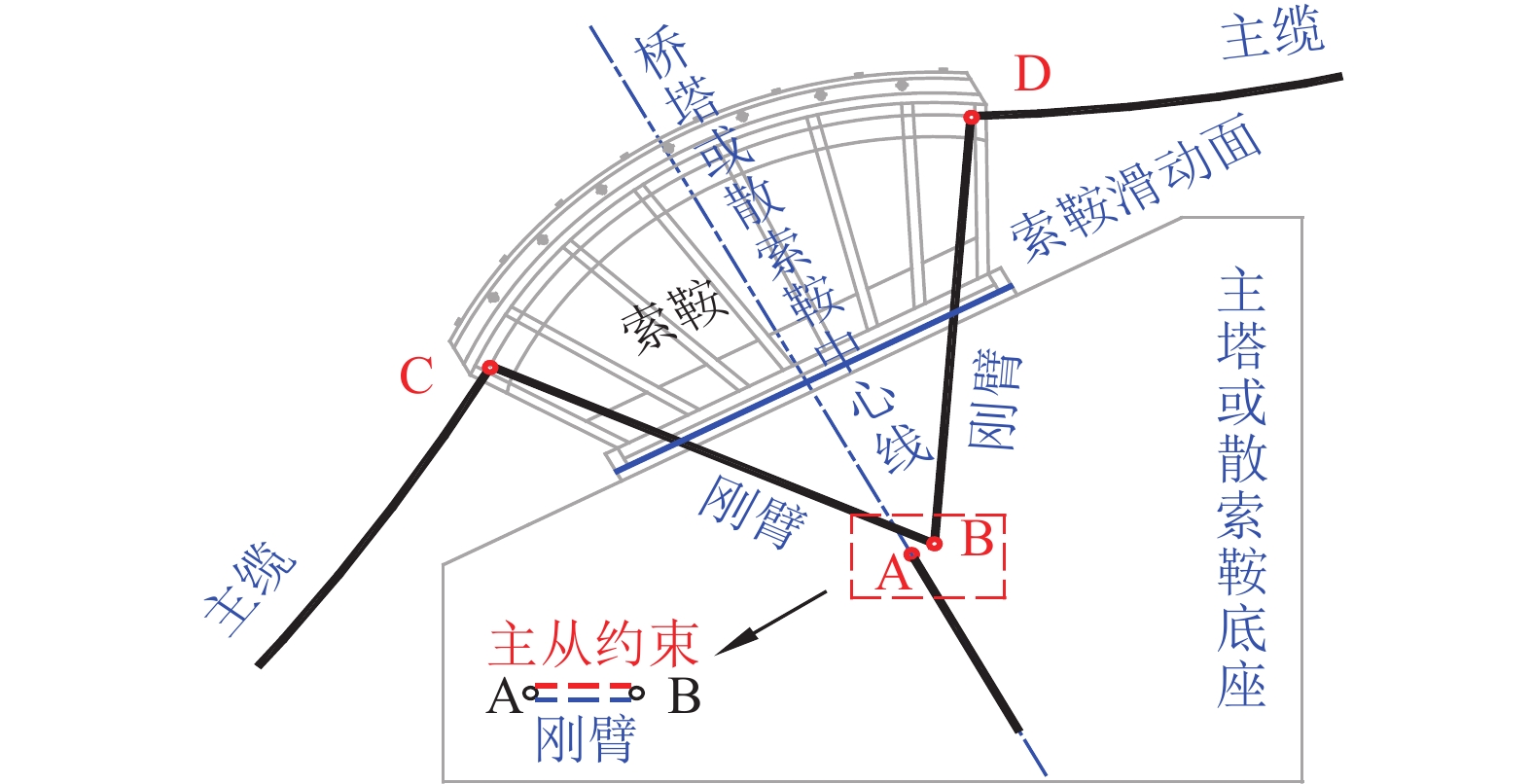
在施工中采用主索鞍可控自由滑移[15]的方式使主索鞍超前就位；如主索鞍没有滑移到预定位置时，通过千斤顶进行顶推。在已建成的桥梁中，也有为了减少主索鞍顶推次数，在施工时适当对主索鞍进行超顶，即顶推前、后主索鞍两侧水平分力的合力出现反向[13]。滑动式散索鞍沿滑动面滑动，减小了主缆跨径和高差；在空缆架设时，散索鞍需向锚跨预偏并临时锁定，而在体系转换过程中释放临时约束。综上所述，对主、散索鞍在体系转换过程中的滑移、顶推和超顶状态，均需在数值仿真计算中进行准确模拟，索鞍有限元模型如图4所示。
图 4 索鞍有限元模型Fig. 4 Finite element model of cable saddle下载:
全尺寸图片
图4中：C、D两点为主缆在成桥状态时与索鞍的切点位置，B点为索鞍圆心点，A点为桥塔塔顶或散索鞍底座中心点。A、B两点通过刚臂和主从约束连接，其中主从约束仅释放滑动面方向约束。当索鞍需固定时，激活刚臂；索鞍需自由滑动时，钝化刚臂；索鞍需超顶时，钝化刚臂，并在B点施加强制位移。
3. 实例分析
3.1 概述
双塔3跨和独塔2跨自锚式悬索桥立面布置如图5所示。
图 5 双塔3跨和独塔2跨自锚式悬索桥立面布置图Fig. 5 General layout of a two-tower-three-span and a single-tower-two-span self-anchored suspension bridges下载:
全尺寸图片
1）双塔3跨自锚式悬索桥
某双塔3跨混凝土自锚式悬索桥桥跨布置形式为（24+65+158+65+24） m，桥梁全长336 m，立面布置如图5（a）所示。图5（a）中：加劲梁采用单箱三室混凝土鱼腹式梁结构，梁高2.2 m；桥塔采用门式结构，塔高50.993 m；该桥塔、梁结构均采用C50混凝土；全桥共设2道主缆，每道主缆由37根索股组成，主缆横向间距为19 m，主缆经滑动式散索鞍锚固于锚箱；吊索采用销接式、铅垂布置，标准段间距为6 m，桥塔两侧吊索间距为7 m；每个吊点设1根吊索，共计41对；吊索锚头调节范围为–90～218 mm。
2）独塔2跨自锚式悬索桥
某独塔2跨自锚式悬索桥桥跨布置形式为（50+115+85+50） m，主桥全长300 m，立面布置如图5（b）所示。图5（b）中：钢梁采用Q345qD钢材，为带挑臂的单箱三室正交异性板结构，梁高2.666 m；桥塔采用C55混凝土，塔高77 m；全桥共设2道主缆，每道主缆由19根索股组成，横向间距为17 m，主缆经滑动式散索鞍锚固于钢箱梁；吊索采用销接式、铅垂布置，纵向间距为6 m，每个吊点设1根吊索，共计31对[24]；吊索锚头调节范围为–115～255 mm。双塔3跨和独塔2跨自锚式悬索桥计算参数见表1。
表 1 双塔3跨和独塔2跨自锚式悬索桥计算参数Table 1 Calculating parameters of two types of self-anchored suspension bridges参数名称 双塔数值 独塔数值 主跨长L主/m 158.000 115.170 边跨长L边/m 56.500 85.000 主跨垂度 f主/m 26.333 12.775 边跨垂度 f边/m 3.166 7.012 主跨高差C主/m 0.000 51.200 边跨高差C边/m 26.958 48.860 主索鞍预偏d主/mm 269.0 160.0 散索鞍预偏d边/mm 39.4 28/24 二期恒载q二/(kN·m–1) 96.7 98.6 加劲梁自重q/(kN·m–1) 461.9 96.6 主缆弹性模量E/GPa 197 197 主缆面积A/m2 0.0729 0.0353 注：1. 独塔散索鞍预偏数值28/24分别表示北山路侧、南山路侧；2. 计算时二期恒载、加劲梁自重需按一半计算。 3.2 主缆垂度分析
首先，根据式（5）和（6）计算S和ΔS，并反算出
$ {f}_{空} $ 和Δf；然后，按式（8）、（9）计算成桥状态下的影响参数；最后，按式（10）、（11）计算并判断Δ是否小于吊索锚杯可调节范围，即可确定第1轮吊索张拉后是否需要对吊索进行接长，其主缆垂度计算结果见表2。计算过程中缆索系统架设时施工的二期恒载按40%计，主索鞍超前就位，预偏距离全部计入；主缆弹性伸长量和滑动式散索鞍滑移量按($ {q}_{梁} $ +0.4$ {q}_{二} $ )与($ {q}_{梁} $ +$ {q}_{二} $ )比值进行计算。表 2 双塔3跨和独塔2跨自锚式悬索桥主缆垂度计算结果Table 2 Main cable sag calculation results of two types of self-anchored suspension bridges计算参数 双塔结果 独塔结果 成桥主跨主缆长S主/m 169.026 128.906 成桥边跨主缆长S边/m 62.949 99.050 主跨主缆弹性伸长ΔS主/m 0.390 0.235 边跨主缆弹性伸长ΔS边/m 0.145 0.180 主跨Δf主/m 1.152 0.922 边跨Δf边/m –0.243 0.216 主跨df主∶dS主 1.262 2.241 边跨df边∶dS边 4.557 3.472 主跨df主∶dL主 –1.183 –2.018 边跨df边∶dL边 –4.100 –2.998 主跨Δ主/m 0.075 0.193 边跨Δ主/m 0.123 0.209 由表2计算结果可知，两座桥梁主、边跨Δ值均小于吊索锚头调节范围，吊索无需接长。由于计算过程中忽略了桥塔、加劲梁压缩变形，其结果偏保守。
3.3 体系转换方案
按图3并结合数值仿真计算，得到两座桥梁的体系转换方案见表3、4。
表 3 双塔3跨自锚式悬索桥体系转换方案Table 3 System transformation scheme of the two-tower-three-span self-anchored suspension bridge施工阶段 施工内容 备注 1 主缆架设，部分二期恒载施工 主、散索鞍临时锁定 2 安装索夹、吊索 — 3 ～ 7 从短至长，分别逐对、对称张拉
$21^{\#} $吊索，直至 $17^{\#} $（ $17'^{\#} $）吊索；
主、散索鞍自由滑动先张拉主跨长出段
对应吊索，并使主索
鞍超前就位8 ～ 15 分别逐对、对称张拉 $1^{\#} $（ $1'^{\#} $）、
$16^{\#} $（ $16'^{\#} $）吊索直至 $8^{\#} $（ $8'^{\#} $）、
$9^{\#} $（ $9'^{\#} $）吊索梁体实现脱架，
完成第1轮张拉16 拆除临时支架 — 17 ～ 27 从桥塔向两侧先长索后短索
分别逐对、对称张拉完成第2轮张拉 28 剩余二期恒载施工 — 由表3可知：在施工阶段1、2中，主缆架设与部分二期恒载并行交叉施工；在施工阶段3～16中，通过张拉主跨长出段对应的
$21^{\#} $ 至$17^{\#} $ （$17'^{\#} $ ）吊索，主索鞍处于可控自由滑动状态，使主索鞍在施工阶段7便到达了成桥位置，在首轮吊索张拉后梁体脱离支架；在施工阶段17～27中，以调整吊索力和加劲梁线形为主要目的。由表4可知：施工阶段3～21中，仅通过张拉主跨长出段对应的
$5^{\#} $ 吊索，主索鞍便到达了成桥位置；而在施工阶段9，再次回到主跨长出段对$4^{\#} $ 吊索进行张拉，其目的是通过调整主索鞍两侧水平分力以改善塔底应力。表 4 独塔2跨自锚式悬索桥体系转换方案Table 4 System transformation scheme of the single-tower-two-span self-anchored suspension bridge施工阶段 施工内容 备注 1 主缆架设，部分二期恒载施工 主、散索鞍
临时锁定2 安装索夹、吊索 — 3 张拉 $5^{\#} $吊索，
主、散索鞍自由滑动先张拉主跨长出
段对应吊索，并使主
索鞍超前就位4 ～ 8 分别逐对、对称张拉 $6^{\#} $（ $31^{\#} $）
吊索，直至 $10^{\#} $ （ $27^{\#} $）吊索— 9 张拉 $4^{\#} $吊索 调整主索鞍两侧
水平分力10 ～ 17 逐对、对称张拉 $11^{\#} $（ $25^{\#} $）
吊索，直至 $18^{\#} $ （ $19^{\#} $）吊索梁体实现脱架，
完成第1轮张拉18 ～ 20 逐对张拉 $3^{\#} $吊索，直至 $1^{\#} $吊索 梁体实现脱架，
完成第1轮张拉21、22 拆除临时支架，
剩余二期恒载施工— 23 ～ 40 从桥塔向两侧先长索后短索
逐对、对称张拉完成第2轮张拉 3.4 体系转换结果分析
由表3、4并通过数值仿真计算得到两座自锚式悬索桥体系转换计算结果，并对结果进行分析。
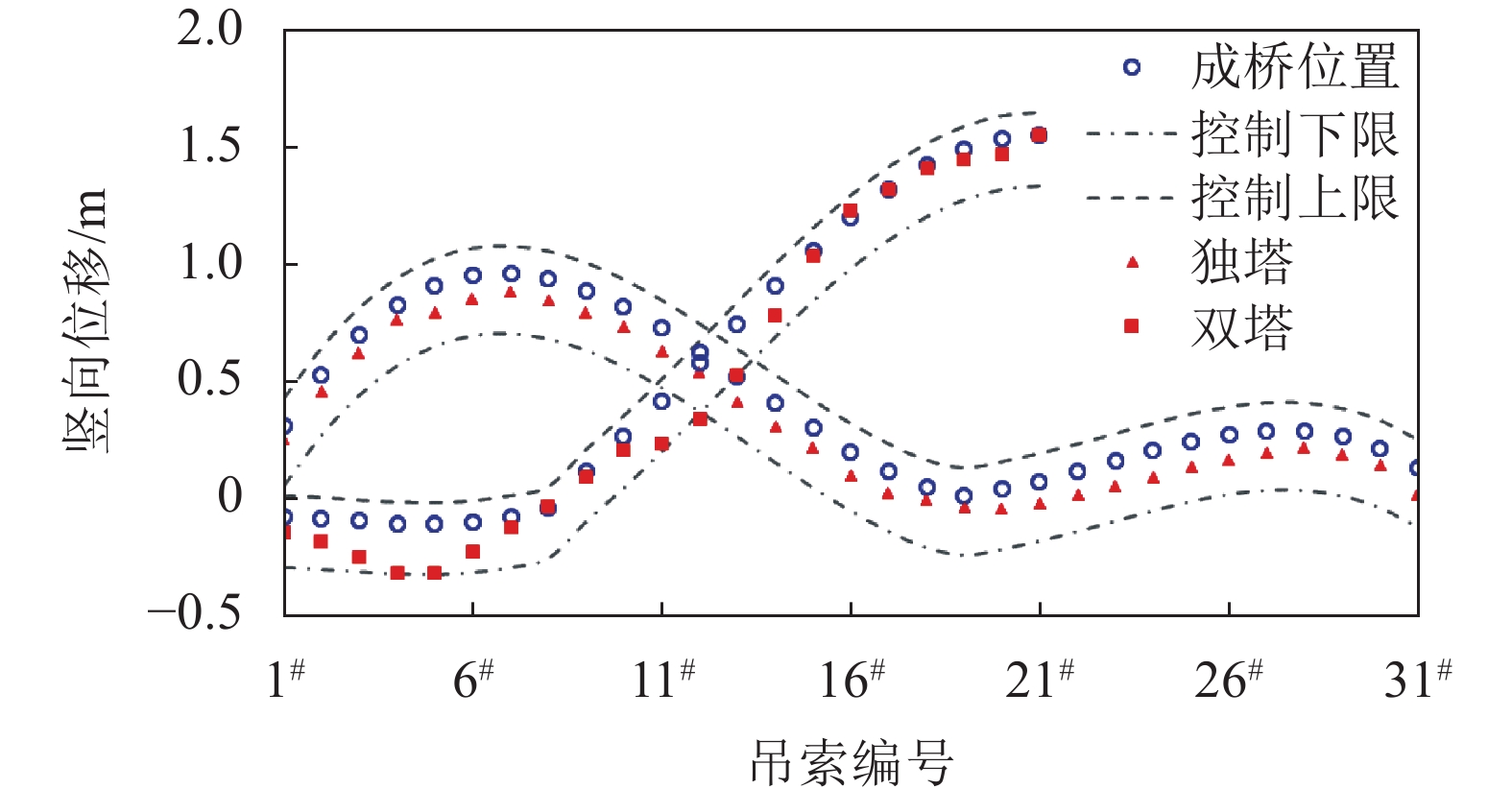
1）第1轮吊索竖向位移
两座自锚式悬索桥第1轮吊索竖向位移如图6所示。由图6可见：控制上限表示在成桥状态下吊索锚环上缘与锚杯上缘平齐时的竖向位移，控制下限表示在成桥状态下吊索锚环下缘与锚杯下缘平齐时的竖向位移。两座自锚式悬索桥在第1轮张拉过程中，吊索竖向位移在控制上、下限范围内，全部吊索均无需接长。
图 6 第1轮张拉后吊索的竖向位移Fig. 6 Vertical displacement of hanger cable in first-round tensioning下载:
全尺寸图片
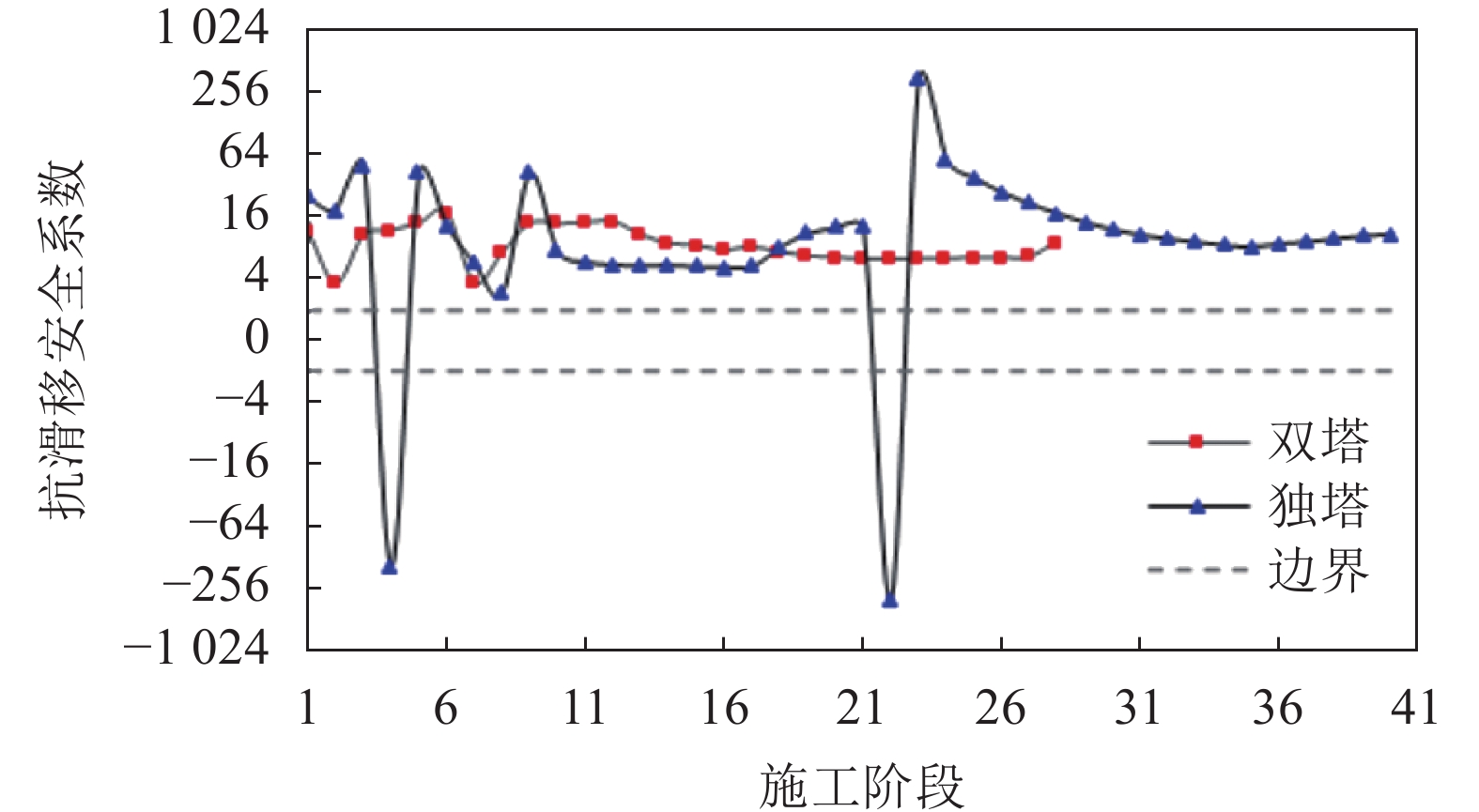
2）抗滑移安全系数
两座自锚式悬索桥主缆与鞍座间的抗滑移安全系数如图7所示。图7中，正值表示主缆轴力边跨侧为紧边拉力，负值表示主缆轴力主跨侧为紧边拉力。两座自锚式悬索桥在体系转换过程中，主缆的抗滑移系数均大于规范[25]要求的限值2。由图7可见：对于独塔自锚式悬索桥，在施工阶段3，张拉主跨长出段
$5^{\#} $ 吊索，主索鞍滑至成桥位置；在施工阶段4，张拉时主跨侧$6^{\#} $ 吊索张拉力大于边跨侧$31^{\#} $ 吊索，使安全系数发生反向变化；在施工阶段9，通过张拉主跨长出段$4^{\#} $ 吊索改善了索鞍两侧主缆的受力，使得安全系数由2.9提高至41.9；在施工阶段22，施工剩余二期恒载，安全系数发生反向变化。对于双塔自锚式悬索桥，在施工阶段3～7，张拉主跨长出段吊索，主索鞍逐渐滑至成桥位置。主索鞍到达成桥位置后，再逐对、对称张拉吊索时，可通过调整主、边跨吊索张拉力来调整抗滑移系数安全系数。
图 7 不同施工阶段主缆与鞍座间的抗滑移安全系数Fig. 7 Safety factors for slippage between main cable and saddle in different construction stages下载:
全尺寸图片
3）桥塔应力历程
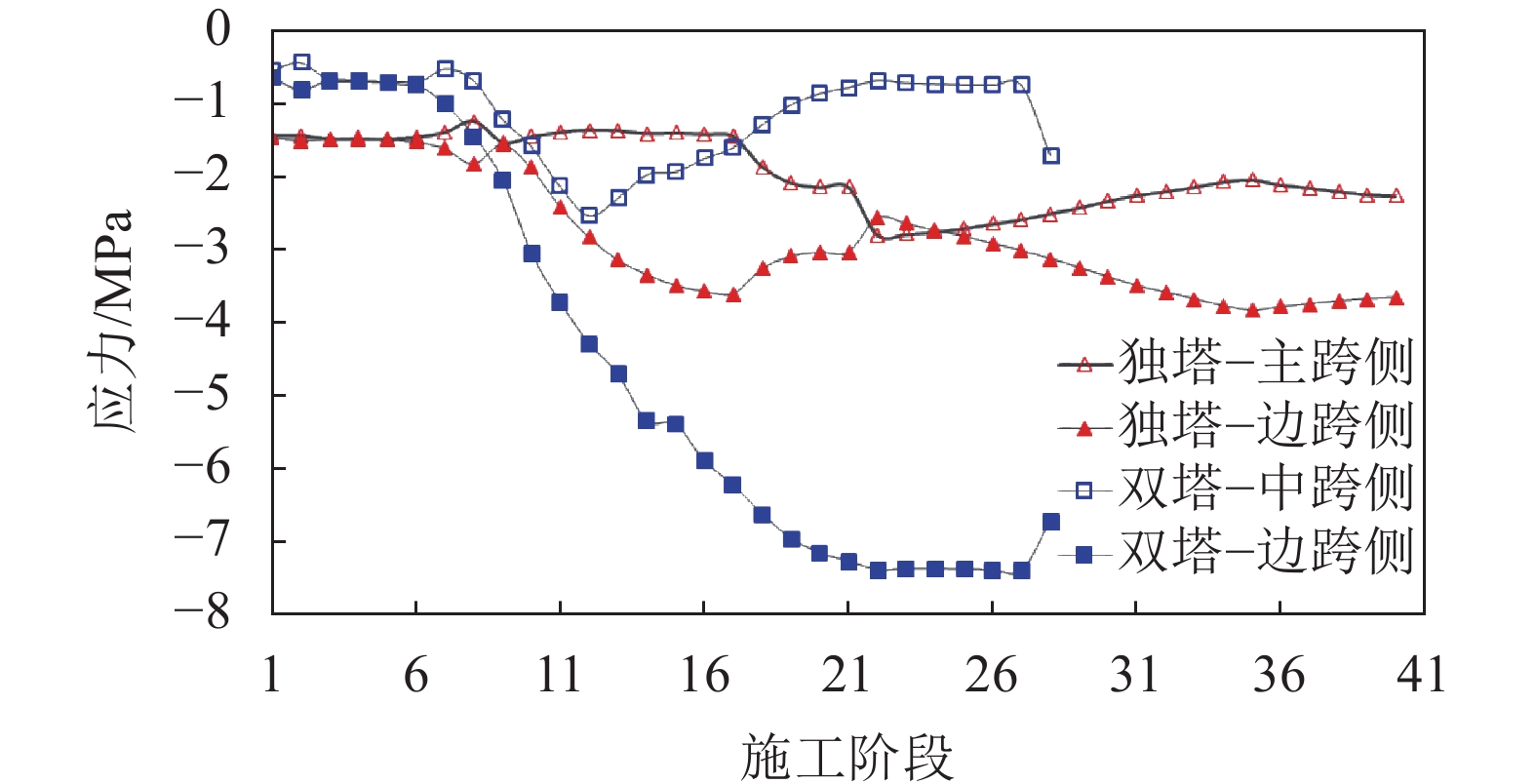
两座自锚式悬索桥塔、梁交界处的桥塔应力如图8所示。由图8可见，两座自锚式悬索桥在体系转换过程中，塔梁交界处的桥塔应力始终处于受压状态，桥塔应力变化平稳，没有伴随主索鞍顶推桥塔应力出现交替变化的情况。
图 8 塔、梁交界处的桥塔应力历程Fig. 8 Variation of stresses in towers at junction of tower and girder下载:
全尺寸图片
通过以上分析可知，本文提出的吊索不接长体系转换方案及索鞍数值模拟方法可行，主缆与鞍座间的抗滑移安全系数和桥塔应力变化平稳，数值仿真计算过程简单。
4. 结 论
以悬索桥主缆抛物线理论为依据，推导出主缆垂度的影响参数，提出3阶段2轮张拉吊索不接长体系转换方案，并以双塔3跨、独塔2跨2座自锚式悬索桥为例进行分析，得出如下结论：
1） 自锚式悬索桥主跨是避免吊索接长的关键桥跨，主缆跨径和主缆长度是影响主缆垂度、避免吊索接长的关键可控参数。
2） 提出吊索不接长的体系转换方案，重点在第1轮吊索张拉时，先逐对张拉主跨长出段吊索，使主索鞍超前就位；再调整吊索力使吊索竖向位移在成桥位置和张拉控制下限之间；第1轮吊索张拉后，使加劲梁脱架，增加主缆弹性伸长，进而增大主缆垂度，从而达到吊索不接长的目的。
3） 对主、散索鞍建立刚臂和主从约束两个边界，通过对刚臂的激活与钝化、设置索鞍节点强制位移，模拟了索鞍在体系转换过程中滑移、固结、超顶的状态。
4） 所提方案已在文中双塔3跨、独塔2跨2座自锚式悬索桥体系转换中使用，2座桥梁均安全、顺利竣工，该方案对类似工程实践具有借鉴意义。
-
图 1 抛物线理论下主缆线形计算图
Fig. 1 Main cable shape calculation diagram under parabolic theory
下载:
全尺寸图片
图 2 不同矢跨比和高跨比变化下主缆垂度变化与主缆长度和跨径变化之比
Fig. 2 Variation curves of ratio of the sag variation to length and span variation of main cable under different sag-span ratio and high-span ratio
下载:
全尺寸图片
图 3 体系转换流程图
Fig. 3 System transformation flow chart
下载:
全尺寸图片
图 4 索鞍有限元模型
Fig. 4 Finite element model of cable saddle
下载:
全尺寸图片
图 5 双塔3跨和独塔2跨自锚式悬索桥立面布置图
Fig. 5 General layout of a two-tower-three-span and a single-tower-two-span self-anchored suspension bridges
下载:
全尺寸图片
图 6 第1轮张拉后吊索的竖向位移
Fig. 6 Vertical displacement of hanger cable in first-round tensioning
下载:
全尺寸图片
图 7 不同施工阶段主缆与鞍座间的抗滑移安全系数
Fig. 7 Safety factors for slippage between main cable and saddle in different construction stages
下载:
全尺寸图片
图 8 塔、梁交界处的桥塔应力历程
Fig. 8 Variation of stresses in towers at junction of tower and girder
下载:
全尺寸图片
表 1 双塔3跨和独塔2跨自锚式悬索桥计算参数
Table 1 Calculating parameters of two types of self-anchored suspension bridges
参数名称 双塔数值 独塔数值 主跨长L主/m 158.000 115.170 边跨长L边/m 56.500 85.000 主跨垂度 f主/m 26.333 12.775 边跨垂度 f边/m 3.166 7.012 主跨高差C主/m 0.000 51.200 边跨高差C边/m 26.958 48.860 主索鞍预偏d主/mm 269.0 160.0 散索鞍预偏d边/mm 39.4 28/24 二期恒载q二/(kN·m–1) 96.7 98.6 加劲梁自重q/(kN·m–1) 461.9 96.6 主缆弹性模量E/GPa 197 197 主缆面积A/m2 0.0729 0.0353 注：1. 独塔散索鞍预偏数值28/24分别表示北山路侧、南山路侧；2. 计算时二期恒载、加劲梁自重需按一半计算。 表 2 双塔3跨和独塔2跨自锚式悬索桥主缆垂度计算结果
Table 2 Main cable sag calculation results of two types of self-anchored suspension bridges
计算参数 双塔结果 独塔结果 成桥主跨主缆长S主/m 169.026 128.906 成桥边跨主缆长S边/m 62.949 99.050 主跨主缆弹性伸长ΔS主/m 0.390 0.235 边跨主缆弹性伸长ΔS边/m 0.145 0.180 主跨Δf主/m 1.152 0.922 边跨Δf边/m –0.243 0.216 主跨df主∶dS主 1.262 2.241 边跨df边∶dS边 4.557 3.472 主跨df主∶dL主 –1.183 –2.018 边跨df边∶dL边 –4.100 –2.998 主跨Δ主/m 0.075 0.193 边跨Δ主/m 0.123 0.209 表 3 双塔3跨自锚式悬索桥体系转换方案
Table 3 System transformation scheme of the two-tower-three-span self-anchored suspension bridge
施工阶段 施工内容 备注 1 主缆架设，部分二期恒载施工 主、散索鞍临时锁定 2 安装索夹、吊索 — 3 ～ 7 从短至长，分别逐对、对称张拉
$21^{\#} $吊索，直至 $17^{\#} $（ $17'^{\#} $）吊索；
主、散索鞍自由滑动先张拉主跨长出段
对应吊索，并使主索
鞍超前就位8 ～ 15 分别逐对、对称张拉 $1^{\#} $（ $1'^{\#} $）、
$16^{\#} $（ $16'^{\#} $）吊索直至 $8^{\#} $（ $8'^{\#} $）、
$9^{\#} $（ $9'^{\#} $）吊索梁体实现脱架，
完成第1轮张拉16 拆除临时支架 — 17 ～ 27 从桥塔向两侧先长索后短索
分别逐对、对称张拉完成第2轮张拉 28 剩余二期恒载施工 — 表 4 独塔2跨自锚式悬索桥体系转换方案
Table 4 System transformation scheme of the single-tower-two-span self-anchored suspension bridge
施工阶段 施工内容 备注 1 主缆架设，部分二期恒载施工 主、散索鞍
临时锁定2 安装索夹、吊索 — 3 张拉 $5^{\#} $吊索，
主、散索鞍自由滑动先张拉主跨长出
段对应吊索，并使主
索鞍超前就位4 ～ 8 分别逐对、对称张拉 $6^{\#} $（ $31^{\#} $）
吊索，直至 $10^{\#} $ （ $27^{\#} $）吊索— 9 张拉 $4^{\#} $吊索 调整主索鞍两侧
水平分力10 ～ 17 逐对、对称张拉 $11^{\#} $（ $25^{\#} $）
吊索，直至 $18^{\#} $ （ $19^{\#} $）吊索梁体实现脱架，
完成第1轮张拉18 ～ 20 逐对张拉 $3^{\#} $吊索，直至 $1^{\#} $吊索 梁体实现脱架，
完成第1轮张拉21、22 拆除临时支架，
剩余二期恒载施工— 23 ～ 40 从桥塔向两侧先长索后短索
逐对、对称张拉完成第2轮张拉 -
[1] Wollmann G P,Ochsendorf J A,Billington D P.Self-anchored suspension bridges[J].Journal of Bridge Engineering,2001,6(2):156–158. doi: 10.1061/(asce)1084-0702(2001)6:2(156 [2] 周绪红,武隽,狄谨.大跨径自锚式悬索桥受力分析[J].土木工程学报,2006,39(2):42–45. doi: 10.3321/j.issn:1000-131X.2006.02.009 Zhou Xuhong,Wu Jun,Di Jin.Mechanical analysis for long-span self-anchored suspension bridges[J].China Civil Engineering Journal,2006,39(2):42–45 doi: 10.3321/j.issn:1000-131X.2006.02.009 [3] 李传习,柯红军,杨武,等.黄河桃花峪自锚式悬索桥体系转换方案的比较研究[J].土木工程学报,2014,47(9):120–127. doi: 10.15951/j.tmgcxb.2014.09.040 Li Chuanxi,Ke Hongjun,Yang Wu,et al.Comparative study on the optimal system transformation schemes for Taohuayu self-anchored suspension bridge[J].China Civil Engineering Journal,2014,47(9):120–127 doi: 10.15951/j.tmgcxb.2014.09.040 [4] 叶庆旱,肖颉,覃勇刚.扬州万福大桥主梁体系转换研究[J].桥梁建设,2016,46(3):57–62. Ye Qinghan,Xiao Jie,Qin Yonggang.Research of system transformation of main girder of Wanfu bridge in Yangzhou[J].Bridge Construction,2016,46(3):57–62 [5] 柯红军.广州猎德大桥体系转换施工方法的确定及实施[J].桥梁建设,2010,40(2):80–83. Ke Hongjun.Determination and implementation of construction method for system transformation of Liede bridge in Guangzhou[J].Bridge Construction,2010,40(2):80–83 [6] 唐贺强,王旋,胡佳安.福州鼓山大桥施工监控[J].桥梁建设,2010,40(5):74–77. Tang Heqiang,Wang Xuan,Hu Jiaan.Construction monitoring and control of Gushan bridge in Fuzhou[J].Bridge Construction,2010,40(5):74–77 [7] 向中富,蒋俊秋,陈桂成,等.自锚式悬索桥体系转换实用计算分析[J].哈尔滨工业大学学报,2021,53(3):164–169. doi: 10.11918/201912069 Xiang Zhongfu,Jiang Junqiu,Chen Guicheng,et al.Practical calculation analysis of system transformation of self-anchored suspension bridge[J].Journal of Harbin Institute of Technology,2021,53(3):164–169 doi: 10.11918/201912069 [8] 周德,张羽龙,王宁波,等.独塔对称自锚式悬索桥简化解析解研究[J].铁道科学与工程学报,2022,19(3):760–767. doi: 10.19713/j.cnki.43-1423/u.T20211031 Zhou De,Zhang Yulong,Wang Ningbo,et al.Simplified analytical solution of symmetrical self-anchored suspension bridge with single tower[J].Journal of Railway Science and Engineering,2022,19(3):760–767 doi: 10.19713/j.cnki.43-1423/u.T20211031 [9] Wang Xiaoming,Wang Huan,Sun Yuan,et al.Process-independent construction stage analysis of self-anchored suspension bridges[J].Automation in Construction,2020,117:103227. doi: 10.1016/j.autcon.2020.103227 [10] 张俊平,黄海云,刘爱荣,等.空间缆索自锚式悬索桥体系转换过程中受力行为的全桥模型试验研究[J].土木工程学报,2011,44(2):108–115. doi: 10.15951/j.tmgcxb.2011.02.003 Zhang Junping,Huang Haiyun,Liu Airong,et al.An overall bridge model test study on the mechanical behaviors in the process of system transformation of self-anchored suspension bridge with spatial cable system[J].China Civil Engineering Journal,2011,44(2):108–115 doi: 10.15951/j.tmgcxb.2011.02.003 [11] 王桢,吴海军,周志祥,等.大跨径自锚式悬索桥吊索索力相邻影响分析[J].土木工程学报,2016,49(6):51–60. doi: 10.15951/j.tmgcxb.2016.06.006 Wang Zhen,Wu Haijun,Zhou Zhixiang,et al.Analysis on near influence of cable force in large-span self-anchored suspension bridges[J].China Civil Engineering Journal,2016,49(6):51–60 doi: 10.15951/j.tmgcxb.2016.06.006 [12] 王桢,吴海军,周志祥,等.大跨径自锚式悬索桥主缆位移特性分析[J].土木工程学报,2015,48(7):102–111. doi: 10.15951/j.tmgcxb.2015.07.011 Wang Zhen,Wu Haijun,Zhou Zhixiang,et al.Displacement characteristics analysis on the main cable of large-span self-anchored suspension bridge[J].China Civil Engineering Journal,2015,48(7):102–111 doi: 10.15951/j.tmgcxb.2015.07.011 [13] 齐东春,王昌将,沈锐利,等.悬索桥施工中鞍座顶推的研究[J].中国工程科学,2010,12(7):68–73. doi: 10.3969/j.issn.1009-1742.2010.07.015 Qi Dongchun,Wang Changjiang,Shen Ruili,et al.Saddle pushing analysis in suspension bridge construction[J].Engineering Sciences,2010,12(7):68–73 doi: 10.3969/j.issn.1009-1742.2010.07.015 [14] 何为,项贻强,徐兴.悬索桥施工中索鞍顶推的小步快跑原则[J].浙江大学学报(工学版),2007,41(1):134–138. doi: 10.3785/j.issn.1008-973X.2007.01.024 He Wei,Xiang Yiqiang,Xu Xing.Frequent short steps saddle pushing principle in suspension bridge construction[J].Journal of Zhejiang University(Engineering Science),2007,41(1):134–138 doi: 10.3785/j.issn.1008-973X.2007.01.024 [15] 孙胜江,王雷刚.悬索桥主索鞍可控状态自由滑移控制[J].桥梁建设,2010,40(1):67–70. Sun Shengjiang,Wang Leigang.Controllable state control of free movement of tower saddle of suspension bridge[J].Bridge Construction,2010,40(1):67–70 [16] 张海顺,王玉银.悬索桥吊索张拉及索鞍顶推降温法数值分析[J].铁道工程学报,2017,34(11):39–44. doi: 10.3969/j.issn.1006-2106.2017.11.009 Zhang Haishun,Wang Yuyin.Cooling method numerical analysis of suspender cable tension and cable saddle pushing[J].Journal of Railway Engineering Society,2017,34(11):39–44 doi: 10.3969/j.issn.1006-2106.2017.11.009 [17] 路韡,王力,谢科,等.独塔自锚式悬索桥吊索力影响参数敏感性分析[J].中国安全生产科学技术,2020,16(9):110–115. Lu Wei,Wang Li,Xie Ke,et al.Sensitivity analysis on influencing parameters of hanger cable force for single-tower self-anchored suspension bridge[J].Journal of Safety Science and Technology,2020,16(9):110–115 [18] 路韡,杨子江,刘世忠,等.西宁文汇桥加劲梁体系转换方案优化[J].桥梁建设,2020,50(3):111–116. doi: 10.3969/j.issn.1003-4722.2020.03.018 Lu Wei,Yang Zijiang,Liu Shizhong,et al.Optimization of system transformation schemes for stiffening girder of Wenhui bridge in Xining[J].Bridge Construction,2020,50(3):111–116 doi: 10.3969/j.issn.1003-4722.2020.03.018 [19] 沈锐利.悬索桥主缆系统设计及架设计算方法研究[J].土木工程学报,1996,29(2):3–9. doi: 10.3321/j.issn:1000-131X.1996.02.001 Shen Ruili.Calculation methods for design and erection of cable curve of suspension bridge[J].China Civil Engineering Journal,1996,29(2):3–9 doi: 10.3321/j.issn:1000-131X.1996.02.001 [20] 唐茂林,强士中,沈锐利.悬索桥成桥主缆线形计算的分段悬链线法[J].铁道学报,2003,25(1):87–91. doi: 10.3321/j.issn:1001-8360.2003.01.018 Tang Maolin,Qiang Shizhong,Shen Ruili.Segmental catenary method of calculating the cable curve of suspension bridge[J].Journal of the China Railway Society,2003,25(1):87–91 doi: 10.3321/j.issn:1001-8360.2003.01.018 [21] Xu Fuyou,Zhang Mingjie,Wang Lei,et al.Self-anchored suspension bridges in China[J].Practice Periodical on Structural Design and Construction,2017,22(1):4016018. doi: 10.1061/(asce)sc.1943-5576.0000304 [22] 唐茂林.大跨度悬索桥空间几何非线性分析与软件开发[D].成都:西南交通大学,2003. Tang Maolin.3D geometric nonlinear analysis of long-span suspension bridge and its software development[D].Chengdu:Southwest Jiaotong University,2003 [23] 史建三.悬索桥大缆架设计算的索长分析法[J].桥梁建设,1993,23(4):30–37. [24] 路韡,杨子江,刘世忠,等.罗家沟自锚式悬索桥体系转换方案研究[J].兰州交通大学学报,2020,39(5):1–5. doi: 10.3969/j.issn.1001-4373.2020.05.001 Lu Wei,Yang Zijiang,Liu Shizhong,et al.Study on the system transformation of Luojiagou self-anchored suspension bridge[J].Journal of Lanzhou Jiaotong University,2020,39(5):1–5 doi: 10.3969/j.issn.1001-4373.2020.05.001 [25] 中华人民共和国交通运输部.公路悬索桥设计规范:JTG/T D65-05—2015[S].北京:人民交通出版社,2016.
