Research on “Grid–Source–Storage–Vehicle” Dynamic Threshold Energy Management Based on Fuzzy Petri Nets
-
摘要: 轨道交通作为电力系统的主要用能对象之一,每年消耗大量电能用于电力机车牵引。因此,降低牵引能耗、提升供能系统的弹性与效能对促进碳达峰、碳中和具有重要的现实意义。轨道交通“网–源–储–车”协同供能系统在传统牵引供电架构的基础上引入了储能系统与新能源发电系统,然而,如何实现牵引负荷、储能系统及新能源发电系统的高效能源自洽,减少双向波动性与不确定性对能量管理系统的影响成为了新的难题。为实现以上目标,减轻牵引负荷对牵引网的功率冲击,延长储能系统的使用寿命,本文提出了一种基于模糊Petri网(fuzzy Petri nets,FPN)的“网–源–储–车”动态阈值能量管理策略。该策略在“网–源–储–车”基本功率分配框架的基础上,设定了多工况下牵引供电系统与储能系统、新能源发电系统的动态能量交互规则,可适用于不同架构的“网–源–储–车”协同供能体系;在此基础上,以电力机车功率与储能系统寿命作为模糊Petri网的输入参数,经过模糊化、Petri网推理、反模糊化等操作后实现对放电阈值的自适应动态调整。本文以某牵引变电所实测数据作为测试案例,仿真结果表明:相较于基于固定阈值的能量管理策略,基于模糊Petri网的动态阈值管理策略能够有效提升能量回馈效率与再生制动能量储存效率,同时,增加光伏发电系统的利用电度,降低电力机车经由接触网从电力系统取能的平均功率及储能系统的平均放电深度;对延长储能系统的预计寿命、提升协同供能系统的能量利用效率与运行经济性具有积极意义。Abstract: As one of the main power customers of the power system, rail transit consumes a large amount of electricity for electric locomotive traction every year. Therefore, reducing the traction energy consumption and improving the resilience and efficiency of the energy supply system are of great practical significance to promote carbon peaking and carbon neutrality. On the basis of the traditional traction power supply structure, the rail transit “grid-source-storage-vehicle” collaborative energy supply system introduces the energy storage system (ESS) and the renewable energy generation system. However, self-consistency of the three (load, the ESS and the renewable energy generation) and reducing the influence of two-way volatility and uncertainty on the energy management systems have become new issues. In order to achieve the above goals, reduce the power impact of the traction load on the traction network, and prolong the service life of the ESS, a “grid-source-storage-vehicle” dynamic threshold energy management strategy based on the fuzzy Petri networks (FPN) was proposed in this paper. Based on the basic power distribution framework of “grid-source-storage-vehicle”, a dynamic energy interaction rules were set in this strategy between the traction power supply system, the ESS and the renewable energy generation system under multiple operating conditions, which could be applied to the “grid-source-storage-vehicle” collaborative energy supply system with different structures. On this basis, the power of electric locomotive and the life of the ESS were taken as the input parameters of the FPN. After that, the adaptive dynamic adjustment of the discharge threshold was realized after the operations of fuzzification, Petri networks reasoning, and de-fuzzification. In this paper, the measured data of a traction substation was taken as a test case. The simulation results showed that, compared with the energy management strategy based on fixed thresholds, the energy feedback efficiency and regenerative braking energy storage efficiency could be effectively improved by the dynamic threshold management strategy based on FPN. At the same time, the utilization of photovoltaic power generation system is increased. The average energy taken by electric locomotives from the power system and the average discharge depth of the ESS are reduced as well, which could prolong the expected life of the ESS and improve the energy utilization of the collaborative energy supply system. To sum up, this strategy has positive significance for extending the expected life of the ESS and improving the energy utilization efficiency and operating economy of the collaborative energy supply system.
-
Keywords:
- rail transit /
- energy storage system (ESS) /
- fuzzy Petri nets /
- dynamic threshold
-
截至2021年底,中国电气化铁路总里程已达15万千米,电气化率为73.3%,电力机车保有量达1.35万台[1]。为降低牵引能耗,响应国家“双碳”战略,基于功率融通架构的轨道交通“网–源–储–车”协同供能系统通过可再生能源与再生制动能量的就地消纳[2],实现高效能、高弹性能源自洽[3-4]。作为“网–源–储–车”协同供能系统的控制中枢,能量管理系统(energy management system,EMS)需要解决电力系统、牵引供电系统、储能系统(energy storage system,ESS)及新能源系统在多工况下的能量分配协同问题[5],缓解双向波动性与不确定性对系统的影响。
从现有文献来看,基于规则类的EMS系统较为完备,复杂程度较低,具有较高的可行性[6-7]。马茜等[8]提出一种适用于地面固定式储能系统的固定阈值能量管理策略,通过设定充放电功率阈值从而控制储能系统的工况切换,但受行车组织方式的影响,会造成“削峰填谷”的峰、谷覆盖面积过低[9-10]及再生制动能量的流失。Gao[11]、Yang[12]等针对城轨储能系统提出了一种基于电压稳定控制的能量管理策略,以电压波动量为基本判据控制能量输出。但电气化铁路牵引功率远高于城轨铁路,其网压波动剧烈,用电压作为控制变量并不合适[13]。邓文丽等[14]建立了多阈值能量管理策略,但在列车运行中牵引功率、储能介质荷电状态的测量均存在一定误差[15-16],且没有自适应效果;诸斐琴[17]、杨浩丰[18]等利用牵引计算预测下一区间牵引能耗,根据储能系统荷电状态设定放电阈值,但该方法计算复杂,难以做到在线优化[19];刘宇嫣等[20]基于模糊控制的EMS系统,将变电站及储能设备的电量变化量及储能设备的实时电量作为模糊系统的输入量,从而实时调整充电与放电阈值。需要注意的是,频繁的深度充放电过程还会对储能介质使用寿命造成影响[21-22],而目前已有的自适应阈值控制策略并未考虑寿命因素的影响,不利于系统长期经济运行。综上所述,现有的能量管理策略在应用场景、复杂程度、智能程度及考虑因素完备性上难以直接适配“网–源–储–车”协同供能系统。
模糊Petri网(fuzzy Petri nets,FPN)是一种融合模糊控制的模型化控制方法,以图形方式阐述控制流程及判别方法,具有鲁棒性强、过程直观等特点,在控制领域应用广泛[23-24],可降低功率、寿命及荷电状态的量测误差对能量管理系统的影响,而目前尚未有学者将该方法引入能量管理系统中。基于以上考虑,为提升再生制动能量的利用效率及延长储能系统的使用寿命,本文提出一种基于模糊Petri网的动态阈值能量管理策略,该方案能够根据外界牵引功率与储能系统的寿命实时动态调整储能系统放电阈值,降低行车组织安排对储能系统利用效率的影响,同时,减缓储能系统的寿命衰减,增加可再生能源利用电度,提升“源–网–储–车”协同供能系统的安全、可靠、经济运行能力。
1. “网–源–储–车”系统基本运行模式
基于功率融通架构的轨道交通“网–源–储–车”协同供能系统在传统结构的基础上增设功率互联设备、储能系统及新能源系统,可实现电能跨区域、跨时间传输,基本结构如图1所示[25]。为实现协同供能系统的高效运行,需要根据列车的基本运行工况,设计不同工况下的能量交互策略及基本工作流程,实现电力系统、牵引供电系统、储能系统及新能源系统的能源自洽。
1.1 牵引工况能量分配策略
电力机车作为“源–网–储–车”协同供能系统的用能主体,需要利用接触网从外界取能。然而列车牵引功率巨大,仅靠新能源系统及储能系统完全供给能量需要配置巨大的功率容量,极大增加配置成本[26]。因此,牵引工况下的电能主要由新能源发电系统、储能系统及电力系统共同供给。为保障系统的安全运行,需要根据电量、功率等参数设计基本运行约束,则在第k个采样区间需要满足的约束如下:
$$\left\{ \begin{gathered} \int_{k - 1}^k {{P_{{\rm{tr}}}}{{\rm{d}}}t = } \int_{k - 1}^k {({P_{{\rm{ess}}}} + {P_{{\rm{ev}}}} + {P_{{\rm{po}}}} - {P_{{\rm{loss}}}})} {{\rm{d}}}t, \\ \int_{k - 1}^k {{P_{{{\rm{re}}}}}{{\rm{d}}}t = } \int_{k - 1}^k {({P_{{\rm{ess}}}} - {P_{{\rm{ev}}}} + {P_{{{\rm{po}}}}} + {P_{{{\rm{loss}}}}})} {{\rm{d}}}t, \\ 0 \leqslant {P_{{{\rm{ev}}}}}(t) \leqslant {P_{{{\rm{ev}}}\_\max }}(t), \\ {P_{{{\rm{ess}}\_{\rm{ab}}\_{\rm{max}}}}} \leqslant {P_{{{\rm{ess}}}}}(t) \leqslant {P_{{{\rm{ess}}\_{\rm{fb}}\_{\rm{max}}}}}, \\ S _{{\rm{SOC}}\_{{\rm{MIN}} }} \leqslant S {_{{\rm{SOC}}}({t})} \leqslant S _{{\rm{SOC}}\_{{\rm{MAX }}}}, \\ {I_{{{\rm{ess}}\_{\rm{ab}}\_{\rm{max}}}}} \leqslant {I_{{{\rm{ess}}}}}(t) \leqslant {I_{{{\rm{ess}}\_{\rm{fb}}\_{\rm{max}}}}} \\ \end{gathered} \right. $$ (1) 式中,Ptr与Pre分别为牵引与再生制动功率,Pess为储能系统功率,Pev为新能源功率,Ppo为牵引供电系统从电力系统取能或能馈功率,Ploss为线路损失功率,Pev_max(t)为t时刻新能源发电最大功率,Pess_ab_max与Pess_fb_max分别为储能系统最大储能和能馈功率,SSOC为储能系统荷电状态,
$ S _{{\rm{SOC}}\_{{\rm{MIN}} }} $ 与$S _{{\rm{SOC}}\_{{\rm{MAX }}}} $ 分别为SSOC上下阈值,Iess为储能系统工作电流,Iess_ab_max与Iess_fb_max分别为储能和能馈电流最大阈值。为积极发挥“削峰填谷”的效果,一方面,当牵引功率大于放电阈值Pthr时,储能系统、新能源系统及电力系统共同输出有功功率并满足功率平衡等式,等式如下:
$${\;\;\;\;\;\;\;\; {P_{{{\rm{tr}}}}}(t) = {P_{{{\rm{ess}}}}}(t) + {P_{{{\rm{ev}}}}}(t) + {P_{{{\rm{po}}}}}(t) - {P_{{{\rm{loss}}}}} }$$ (2) 另一方面,若牵引功率未达到放电阈值或储能系统荷电状态越限,此时牵引功率由电力系统单独供给,新能源发电能量将由储能系统进行吸收,功率方程如下:
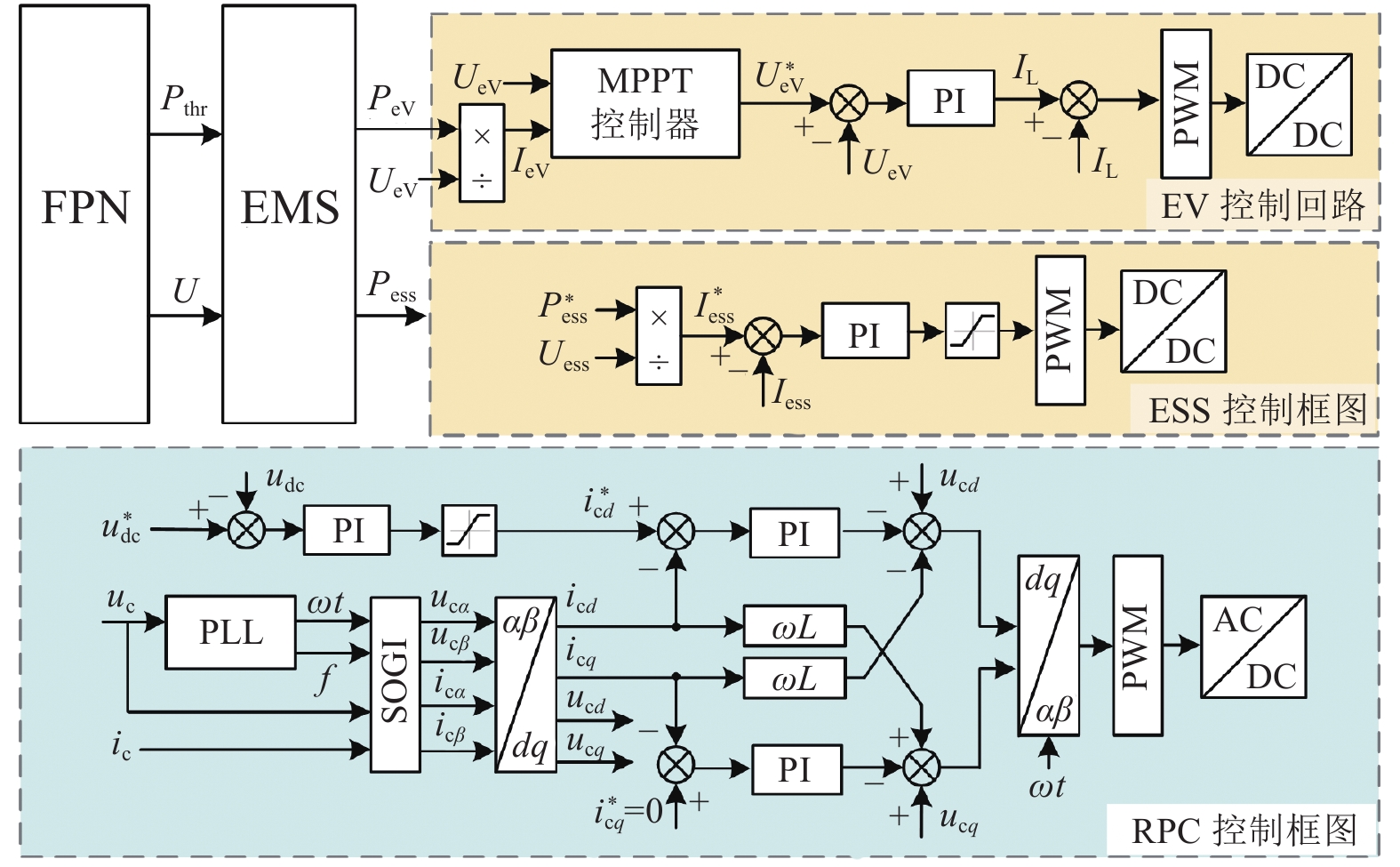
$$\begin{aligned}[b]& {P_{{{\rm{tr}}}}}(t) = {P_{{{\rm{po}}}}}(t) - {P_{{{\rm{loss}}}}}{\text{ }}({P_{{{\rm{tr}}}}} \lt {P_{{{\rm{thr}}}}}) \vee {P_{{{\rm{ess}}}}}(t) = \\&\qquad {P_{{{\rm{ev}}}}}(t),{\text{ }}S _{\rm{SOC}} \lt S _{{\rm{SOC}}\_{{\rm{MIN}} }} \end{aligned}$$ (3) 需要注意的是,为实现功率的可控流动,各DC/DC变换器均采用电压电流双环控制策略,各子系统根据EMS指导功率及当前直流母线网压,计算目标电流,输入双环控制系统,从而实现可控功率流动,如图2所示。
图2中,Uev、Iev分别为光伏发电系统电压与电流,IL为电感电流,udc为RPC直流母线电压,uc、ic分别为RPC控制电压与电流,ucα、ucβ、icα和icβ分别为正交坐标系下的控制电压与电流,ucd、ucq、icd和icq分别为dq坐标系下的控制电压与电流,另外,参考物理量以“*”表示。
1.2 再生制动工况能量分配策略
当电力机车进行再生制动时,其动能将转化为电能,并由受电弓反馈给接触网。为提升再生制动能量利用效率,将其由储能系统进行吸收,多余再生制动能量将返送电力系统,功率平衡方程如下:
$${\;\;\;\;\;\;\; {P_{{{\rm{re}}}}}(t) = {P_{{{\rm{ess}}}}}(t) - {P_{{{\rm{ev}}}}}(t) + {P_{{{\rm{po}}}}}(t) + {P_{{{\rm{loss}}}}} }$$ (4) 当储能系统荷电状态达到上阈值时,储能系统退出工作,新能源系统不再向直流母线馈能,列车再生制动能量全部返送电力系统,功率平衡方程如下:
$$ {\;\;\;\;\left\{ \begin{gathered} {P_{{{\rm{re}}}}}(t) = {P_{{{\rm{po}}}}}(t) + {P_{{{\rm{loss}}}}}{\text{, }}S _{{\rm{SOC}}} \gt S _{{\rm{SOC}}\_{{\rm{MAX }}}}; \\ {P_{{{\rm{ess}}}}}(t) = {P_{{{\rm{ev}}}}}(t) = 0{\text{, }}S _{{\rm{SOC}}} \gt S _{{\rm{SOC}}\_{{\rm{MAX }}}} \\ \end{gathered} \right.} $$ (5) 当供电臂内没有功率需求时(如机车惰行),储能系统将吸收新能源发电能量,减少弃光弃风等资源浪费,功率平衡方程如下:
$$ \left\{ \begin{gathered} {P_{{{\rm{re}}}}}(t) = {P_{{{\rm{po}}}}}(t) = 0,{\text{ }}S _{{\rm{SOC}}} \in [S _{{\rm{SOC}}\_{{\rm{MIN}} }},S _{{\rm{SOC}}\_{{\rm{MAX }}}}];{\text{ }} \\ {P_{{{\rm{ess}}}}}(t) = {P_{{{\rm{ev}}}}}(t),{\text{ }}S _{{\rm{SOC}}} \in [S _{{\rm{SOC}}\_{{\rm{MIN}} }},S _{{\rm{SOC}}\_{{\rm{MAX }}}}] \\ \end{gathered} \right. $$ (6) 综上所述,各工况下的功率分配见表1。
表 1 多工况功率分配Table 1 Multi-condition power distribution列车工况 功率平衡方程 基本判据 牵引 $ {P}_{\text{tr} }={P}_{\text{po} }-{P}_{\text{loss} } $,
${P}_{\text{ess} }={P}_{\text{ev} }(储能系统充电) $牵引功率小于阈值 ${P_{ {{\rm{tr}}} } } = {P_{ {{\rm{ess}}} } } + {P_{ {{\rm{ev}}} } } + {P_{ {{\rm{po}}} } } - {P_{ {{\rm{loss}}} } }$ 牵引功率大于阈值 ${P}_{\text{tr} }={P}_{\text{po} }-{P}_{\text{loss} }$,
${P}_{\text{ess} }={P}_{\text{ev} }(储能系统充电) $牵引功率大于阈值,
SSOC越限再生制动 ${P_{ {{\rm{re}}} } } = {P_{ {{\rm{ess}}} } } - {P_{ {{\rm{ev}}} } } + {P_{ {{\rm{po}}} } } + {P_{ {{\rm{loss}}} } }$ SSOC
未越限$ {P_{ { {\rm{re} } } } } = {P_{ { {\rm{po} } } } } + {P_{ { {\rm{loss} } } } } $,
${ {P_{ { {\rm{ess} } } } } = {P_{ { {\rm{ev} } } } } = 0 \qquad }$SSOC
越限惰行/空闲 ${P}_{\text{re} }={P}_{\text{po} }=0$,
$ {P}_{\text{ess} }={P}_{\text{ev} }(储能系统充电) $SSOC
未越限${P_{ { {\rm{re} } } } } = {P_{ { {\rm{po} } } } } = 0$,
$ {P_{ { {\rm{ess} } } } } = {P_{ { {\rm{ev} } } } } = 0 $SSOC
越限1.3 能量管理系统工作流程
完成制定各工况下的能量分配策略后,完善参数输入及后续数据处理环节。一方面,为实现放电阈值随牵引功率及储能系统寿命动态调整的效果,先对数据进行定义及处理。当列车运行时,牵引变电所可测得牵引网电压及电流,得到t时刻的列车牵引功率Ptr(t)或制动功率Pre(t),进行1阶平滑处理如下:
$$ \left\{ \begin{gathered} {P_{{{\rm{tr}}}}}(t) = \frac{{\Delta t}}{\tau }{P_{{{\rm{or}}}}}(t) + \frac{{\tau - \Delta t}}{\tau }{P_{{{\rm{or}}}}}(t - \Delta t),{P_{{{\rm{or}}}}} \gt0; \\ {P_{{{\rm{re}}}}}(t) = \frac{{\Delta t}}{\tau }{P_{{{\rm{or}}}}}(t) + \frac{{\tau - \Delta t}}{\tau }{P_{{{\rm{or}}}}}(t - \Delta t),{P_{{{\rm{or}}}}} \leqslant0 \\ \end{gathered} \right. $$ (7) 式中,Por为通过测量得到的t时刻的原始列车功率,τ为时间常数,∆t为采样时间间隔。
另一方面,根据储能系统剩余寿命近似经验公式[27],将不同放电深度下的寿命损失折算到100%放电深度下,从而得到剩余寿命参考值L,即:
$$ L = 1 - \dfrac{{\displaystyle\sum\limits_{k=1}^{\infty} {\dfrac{{{N_{{{\rm{pls}}}}}(D_{{100{\text{%}} }})}}{{{N_{{{\rm{pls}}}}}(D(t))}}} }}{{{N_{{{\rm{pls}}}}}(D_{{100{\text{%}} }})}},{\text{ }}L \in [0,1] $$ (8) 式中,Npls(D(t))为t时刻在放电深度D(t)下储能系统最大循环寿命,Npls(D100%)为100%放电深度下ESS最大循环寿命。Npls(D(t))采用4阶曲线拟合,如下:
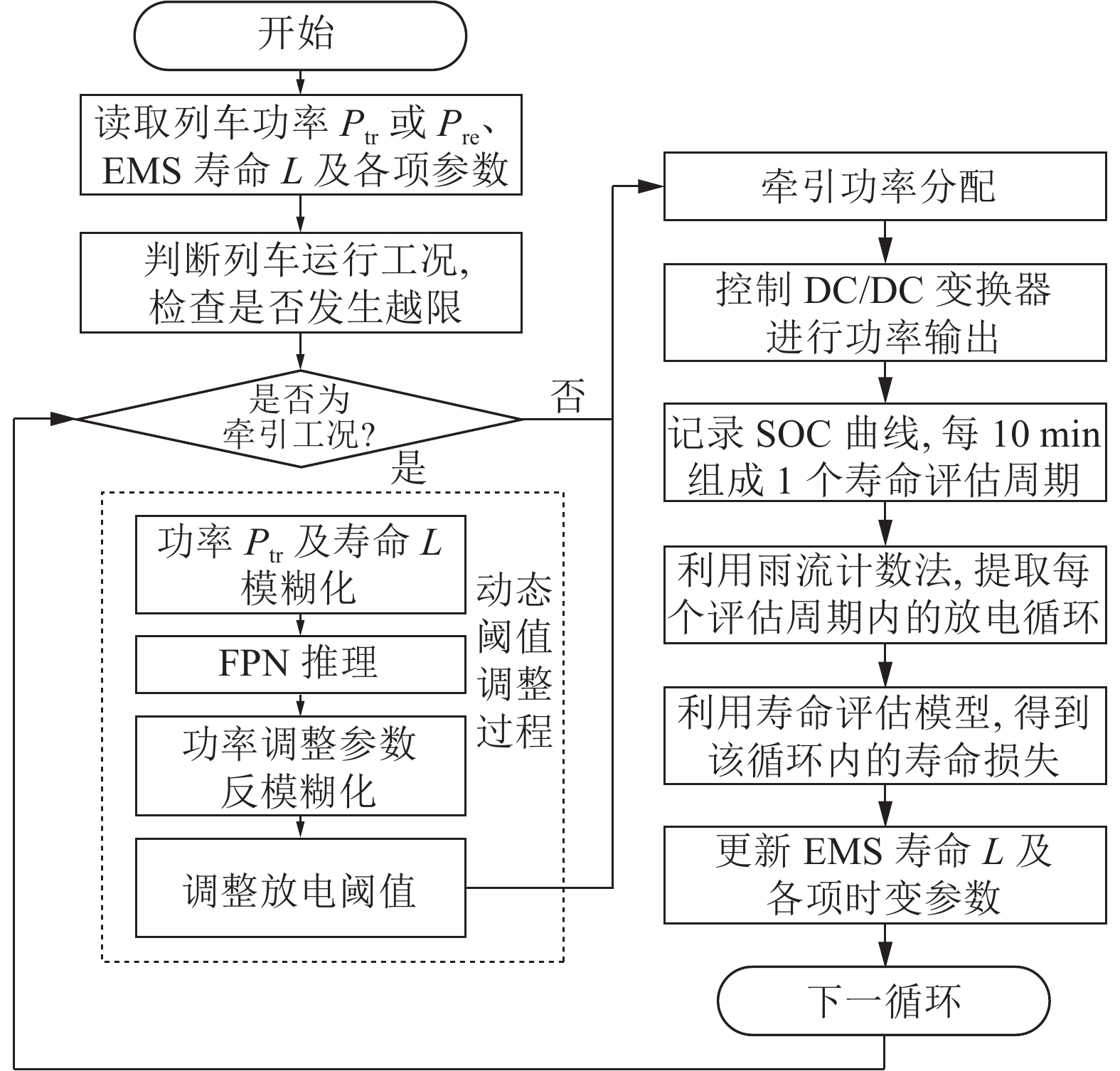
$$ \begin{aligned}[b] {N_{{{\rm{pls}}}}}(D(t)) =& aD(t)_{}^4 + bD(t)_{}^3+ \\& cD(t)_{}^2 + dD(t)_{}^1 + e \end{aligned} $$ (9) 式中,a、b、c、d和e均为拟合参数。当完成基本参数的初始化后,各参数输入模糊Petri网中,得到t时刻的动态阈值Pthr(t);再根据牵引工况进行功率分配及能量输出。完成功率分配后,利用雨流计数法等方式提取放电循环深度,更新储能系统寿命及储能系统SSOC数值,并开始下一循环。能量管理流程如图3所示。
2. 基于FPN的ESM动态阈值调整模型
FPN是一种融合模糊控制的模型化控制方法。一方面,FPN以图形方式阐述控制流程及判别方法,使得复杂控制逻辑形象化;另一方面,FPN以模糊控制作为基础,对降低功率、寿命及荷电状态的量测误差的影响具有积极作用。
2.1 输入量的模糊化
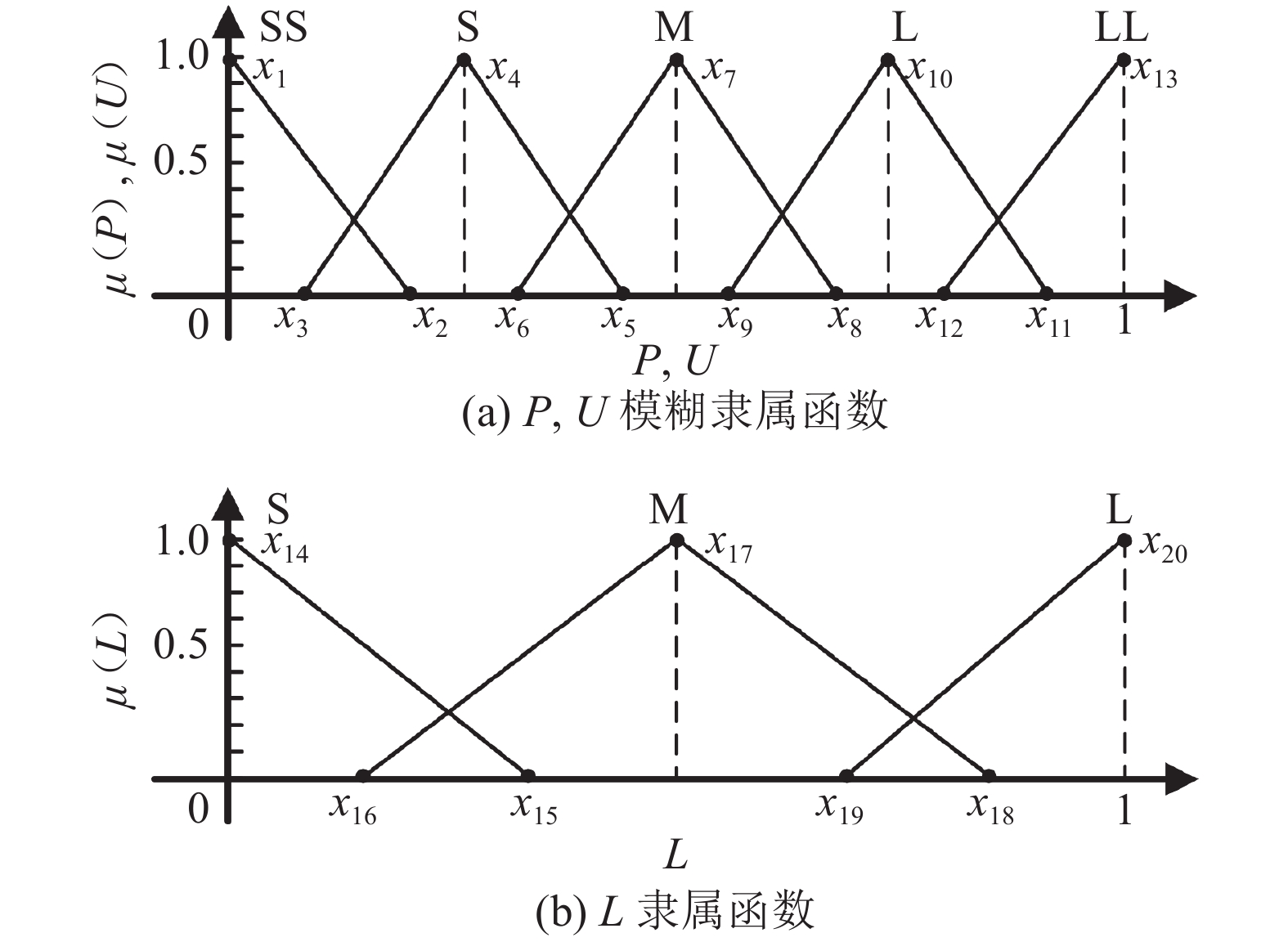
FPN的输入、输出均为模糊量,因此,需要对牵引功率及储能系统寿命进行模糊化处理。输入量模糊隶属函数μ (L)、μ (P)与输出量模糊隶属函数μ (U)均采用三角隶属函数,如图4所示。牵引功率输入量P及阈值调整参数输出量U均采用逻辑语言“SS、S、M、L、LL”来表示“非常小、小、中等、大、非常大”,ESS寿命输入量L采用逻辑语言“S、M、L”表征“小、中、大”,x为三角隶属函数特征点,用于调整函数覆盖范围,隶属函数如图4所示。
作为FPN的输入,需要将牵引功率映射到[0,1]区间以便于模糊描述,映射规则如下:
$$ {P}_{\text{fu}}^{}=\left\{ \begin{array}{l}\dfrac{{P}_{\text{tr}}-{P}_{\text{down}}}{{P}_{\text{up}}-{P}_{\text{down}}}\text{,}\text{ }\dfrac{{P}_{\text{tr}}-{P}_{\text{down}}}{{P}_{\text{up}}-{P}_{\text{down}}}\in [0,1];\\ {P}_{\text{fu}}^{}=1,\text{ }\dfrac{{P}_{\text{tr}}-{P}_{\text{down}}}{{P}_{\text{up}}-{P}_{\text{down}}} \gt 1;\\ {P}_{\text{fu}}^{}=0,\text{ }\dfrac{{P}_{\text{tr}}-{P}_{\text{down}}}{{P}_{\text{up}}-{P}_{\text{down}}} \lt 0\end{array}\right. $$ (10) 式中,Pfu为模糊功率参数,Pup与Pdown分别为功率映射区间上下界。当得到Pfu后,还需通过三角隶属函数进行运算,得到不同模糊子集的隶属程度。需要注意的是,储能系统剩余寿命已在[0,1]区间,无需进行映射操作。
2.2 FPN的控制模型
FPN拥有多种表示方法[28],本文采用一个7元数组进行表示,设存在m个库所,n个变迁节点,o个命题,则FPN表示为:
$$ {\rm{FPN}} = (P,T,D,{\boldsymbol{\alpha ,\beta },{\boldsymbol{T}}_{\rm{h}},{\boldsymbol{U}}}) $$ (11) 式中:P为库所(place)的集合,
$P = \{ {p_1},{p_2},\cdots,{p_m}\}$ ,用于表示功率、寿命基本参数状态,用“○”图形表示,其中包含的节点数量为托肯(token),用“●”表示;T为变迁节点的集合,$T = \{ {t_1},{t_2},\cdots,{t_n}\}$ ,用于表征库所的状态变化,用“|”表示;D为命题集合,$D = \{ {d_1}, {d_2},\cdots,{d_o}\}$ ,用于反映命题规则,表征P与T的有向关系;${\boldsymbol{\alpha }}$ 为库所对应命题的可信度,$\;{\boldsymbol{\beta }}$ 表征库所节点和命题之间的对应关系;Th为各变迁节点的定义阈值,${\boldsymbol{T}}_{\rm{h}} = [{\lambda _1},{\lambda _2},\cdots,{\lambda _n}]$ ,是能否变迁的判别条件;U为规则置信度矩阵,${\boldsymbol{U}} = {\rm{diag}}({\mu _1},{\mu _2},\cdots,{\mu _n})$ 。在该模型中,为表征模糊功率、模糊寿命及模糊阈值调整参数的对应关系,需要建立基本的模糊规则,见表2。根据表2中规则,若储能系统寿命的模糊度为S,牵引功率的模糊度为SS,则阈值调整参数的的模糊度为SS,其他对应关系可类推。
表 2 阈值调整模糊规则Table 2 Threshold adjustment fuzzy rules牵引功率P 阈值调整参数U 寿命 L=S 寿命 L=M 寿命 L=L SS SS SS S S SS S M M S M L L M L LL LL L LL LL 需要注意的是,在FPN的推理环节中,各模糊规则会进行交叉、复合,经过多重运算后得到输出参数的各模糊子集的权重值。以模糊寿命库所
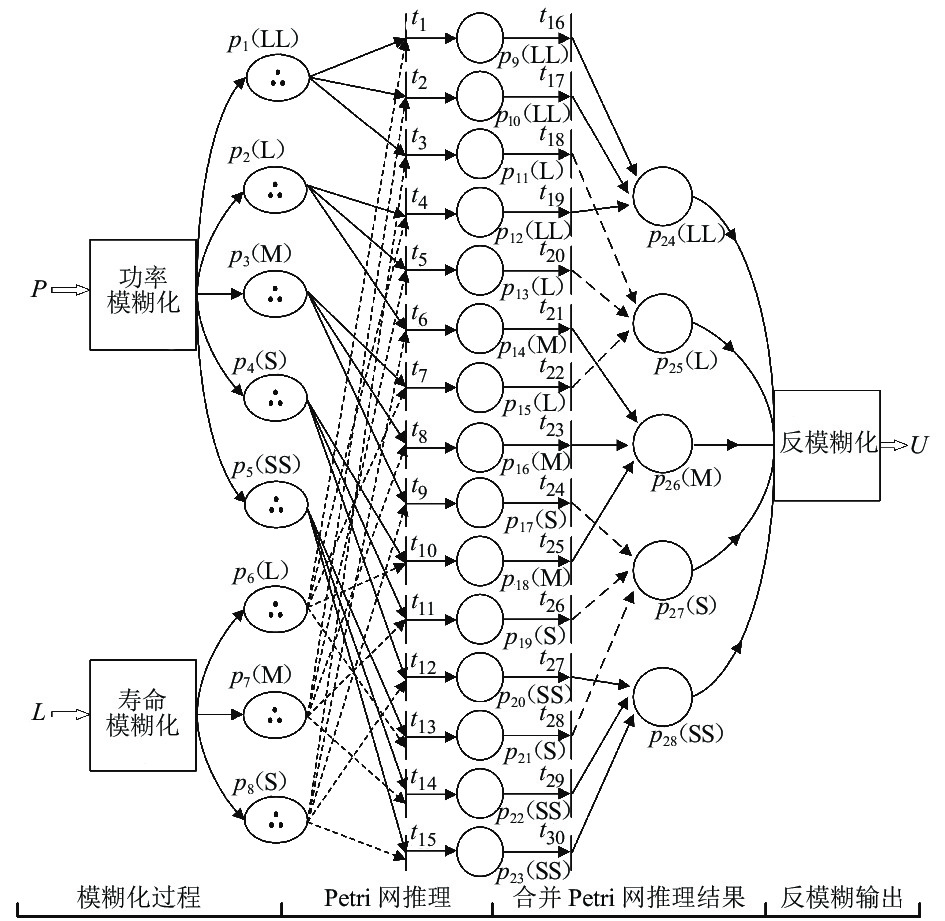
$\{ {p_1}, {p_2},\cdots, {p_8}\}$ 到结果库所$\{ {p_{24}},{p_{25}},\cdots,{p_{28}}\}$ 的变迁为例,若省去中间推理环节,FPN可看作是多条产生式规则的复合,即:$$ \begin{aligned}[b]& R(i){\text{: IF }}{p_1}{\text{(}}i{\text{) AND }}{p_2}{\text{(}}i{\text{)}}{\text{AND }}\cdots{\text{AND }}{p_8}{\text{(}}i{\text{)}} \\& {\text{ THEN }}{p_{24}}{\text{(}}i{\text{) AND }}{p_{25}}{\text{(}}i{\text{) AND}}\cdots{\text{AND }}{p_{28}}{\text{(}}i{\text{) }} \end{aligned}$$ (12) 综上所述,基于FPN的阈值调整模型如图5所示。该模型由4层结构组成,当采集牵引功率与储能系统寿命后,首先,进行模糊化处理,为
$ \{ {p_1},{p_2},\cdots,{p_5}\} $ 及$ \{ {p_6},{p_7},{p_8}\} $ 两个模糊寿命库所赋予初始托肯,各库所根据所含托肯数目及线路变迁阈值自动进行推理,推理结果存放在中间结果库所$ \{ {p_9},{p_{10}},\cdots,{p_{23}}\} $ 中;再通过变迁$ \{ {t_{16}},{t_{17}},\cdots,{t_{30}}\} $ 对中间推理结果进行汇总,得到功率调整参数U的各模糊子集隶属函数的对应数值;最后,通过反模糊化处理得到最终数值。2.3 FPN的推理
当完成模糊化过程后,系统会赋予模糊功率库所初始托肯数值M0,即:
$$ {\;\;\;\;\;{M_0} = ({M_0}({p_1}),{M_0}({p_2}),\cdots,{M_0}({p_8}))} $$ (13) 根据表2所罗列的阈值调整模糊规则,从初始输入量到中间库所
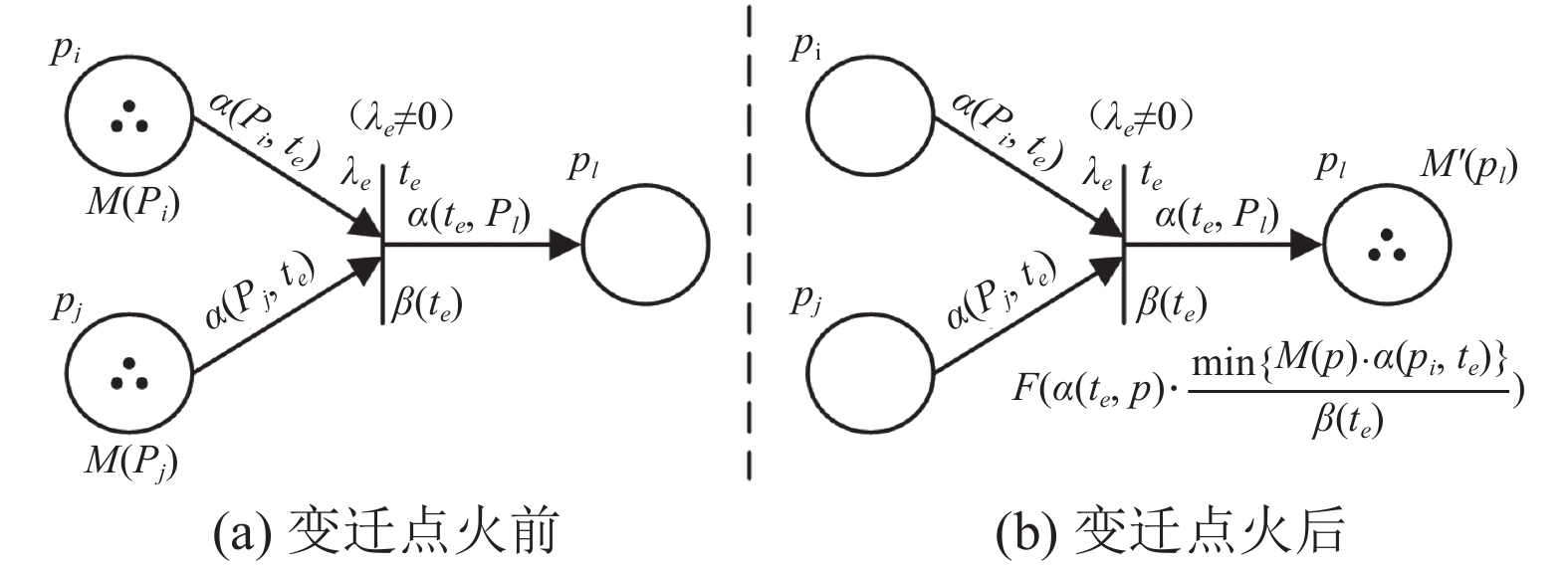
$ {\text{\{}}{p_9},{p_{10}},\cdots,{p_{23}}{\text{\} }} $ 的推理采用如下产生式规则:$$ \begin{aligned}[b] {R_{1 - 15}}: {\text{ IF }}&{p_i}{\text{ AND }}{p_j}{\text{ THEN }}{p_l}, \\& {\text{ }}{p_i} \in \{ {p_1},\cdots,{p_5}\} ,{p_j} \in \{ {p_6},{p_7},{p_8}\} , \\& {\text{ }}{p_l} \in \{ {p_9},{p_{10}},\cdots,{p_{23}}\} \\ \end{aligned}$$ (14) 式中,
$ {R_{1 - 15}} $ 为初始输入量到中间库所的推理规则,i、j、l均为序号角标。库所与变迁的对应关系由命题进行表示(如p1对应t1),而每一个命题都具有置信度$ \alpha $ ,若某变迁的所有前向库所满足条件式(15),则代表该变迁可以发生。$${\;\;\;\;\; M({p_i}) \cdot \alpha ({p_i},{t_e}) \geqslant {\lambda _e},{\text{ }}{t_e} \in T,\forall {p_i} \in {}^ \bullet {t_e} }$$ (15) 式中,e为序号角标,
$ M({p_i}) $ 为库所pi的托肯值,$ \alpha ({p_i},{t_e}) $ 为库所到变迁的置信度,$ {\lambda _e} $ 为变迁的阈值,$ {}^ \bullet {t_e} $ 为变迁te的前集。当满足变迁条件时,变迁te会产生新标志
$ M' $ ,并赋予给te的后向库所pl托肯值,推理过程如图6所示。其计算方法如下:
$${\;\;\;\;\; M'({p_l}) = F\left(\alpha ({t_e},p) \cdot \frac{{\min \{ M(p) \cdot \alpha ({p_i},{t_e})\} }}{{\beta ({t_e})}}\right)} $$ (16) 式中,F(x)为映射函数,定义如下:
$$ F(x) = \left\{ \begin{gathered} x,{\text{ }}x \in (0,1); \\ 1,{\text{ }}x \geqslant 1 \\ \end{gathered} \right. $$ (17) 从中间库所
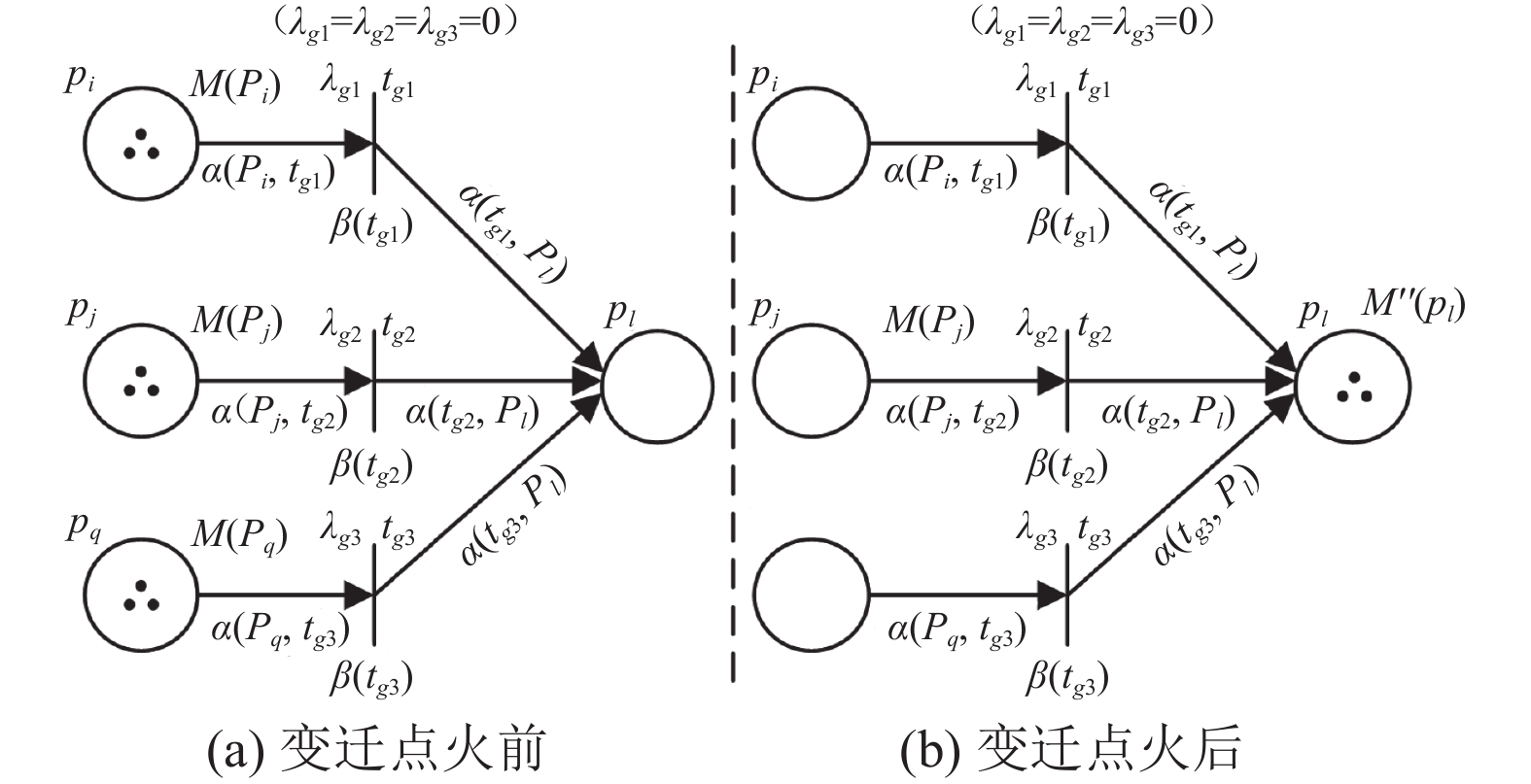
${{\{ }}{p_9},{p_{10}},\cdots,{p_{23}}{{\} }}$ 到结果库所${{\{ }}{p_{24}},{p_{25}},\cdots, {p_{28}}{{\} }}$ 的推理采用如下规则:$$\begin{aligned}[b] {R_{16 - 30}}: {\text{ IF }}&{p_i}{\text{ OR }}{p_j}{\text{ OR }}{p_q}{\text{ THEN }}{p_l}, \\& {\text{ }}{p_i}{\text{, }}{p_j}{\text{, }}{p_q} \in \{ {p_9},{p_{10}},\cdots,{p_{23}}\} ,{\text{ }}{p_i} \ne {p_j} \ne {p_q}, \\& {\text{ }}{p_l} \in \{ {p_{24}},{p_{25}},\cdots,{p_{28}}\} \\[-10pt] \end{aligned}$$ (18) 式中,
$ {R_{16 - 30}} $ 为中间库所到结果库所的推理规则,i、j、q、l均为序号角标。此时变迁条件与式(15)相同。设g为变迁序号,当发生变迁后,变迁会产生新的标志$ M'' $ 并赋予给后向库所pl的新托肯值,推理过程如图7所示。其计算方法如下:
$$ M''({p_l}) = F(\alpha ({t_g},p) \cdot \frac{{\max \{ M(p) \cdot \alpha (p,{t_g})\} }}{{\beta ({t_g})}}) $$ (19) 2.4 FPN的结果输出
经模糊化、推理、合并等步骤后,FPN将功率调整参数U的各模糊子集对应函数的数值以托肯的形式存储在结果库所
$ \{ {p_{24}},{p_{25}},\cdots,{p_{28}}\} $ 中。需要注意的是,该托肯表示各模糊子集对调整参数U的隶属程度,仍然属于模糊量,需要经过反模糊化处理才能使用。本文采取加权平均法进行反模糊化处理,得到阈值调整参数U,即:$$ U = \frac{{\displaystyle\sum\limits_{i=24}^{28} {M({p_i}) \cdot {\mu _{{p_i}}}(M({p_i}))} }}{{\displaystyle\sum\limits_{i=24}^{28} {{\mu _{{p_i}}}(M({p_i}))} }} $$ (20) 式中:
${\mu _{{p_i}}}(M({p_i})) $ 为第i个库所中托肯所对应的模糊隶属函数数值;该参数用于调整放电阈值波动范围Prange。设t时刻的阈值调整参数为U(t),放电阈值基准值为Pbase,动态阈值Pthr可表示如下:$$ {P_{{{\rm{thr}}}}}(t) = {P_{{{\rm{base}}}}} + U(t){P_{{{\rm{range}}}}} $$ (21) 当得到动态阈值后,根据牵引工况或再生制动工况下的能量分配策略,利用电压电流双环控制策略实现功率的可控输出、输入。
3. 算例分析
为验证基于FPN的可变阈值控制策略的有效性,将基于实际牵引供电系统数据,针对功率输出特性、储能系统寿命衰减、充放电特性及运行效率等参数进行横向比较,展示该策略的优越性。
3.1 仿真条件及参数
本文以装配钛酸锂电池储能系统与光伏发电新能源系统的轨道交通协同供能系统作为研究对象,以某牵引变电所的实测功率数据与典型光伏日发电曲线为数据源,功率如图8所示,系统其他基本参数见表3。
表 3 系统基本参数Table 3 System basic parameters系统参数 数值 ESS额定功率/MW 3.2 ESS额定容量/kWh 331.2 ESS荷电状态范围 (0.25,0.85) 光伏发电装机容量/MW 2.0 固定放电阈值/MW 7.0 放电阈值基准值/MW 6.4 放电阈值波动范围/MW 6.4 牵引能量总电度/kWh 20 943.3 再生制动能量总电度/kWh 4 788.2 为了比较不同策略的能量利用效率,定义能量回馈效率ηfe和储能效率ηab来反映储能系统在列车牵引条件和再生制动条件下的能量利用水平,如下:
$$ \left\{ \begin{gathered} {\eta _{{{\rm{fe}}}}} = \frac{{\displaystyle\sum {{P_{{{\rm{fe}}}}}(t)\Delta t} }}{{\displaystyle\sum {{P_{{{\rm{tr}}}}}(t)\Delta t} }}, \\ {\eta _{{{\rm{ab}}}}} = \frac{{\displaystyle\sum {{P_{{{\rm{ab}}}}}(t)\Delta t} }}{{\displaystyle\sum {{P_{{{\rm{re}}}}}(t)\Delta t} }} \\ \end{gathered} \right. $$ (22) 式中,Pfe与Pab分别为ESS的能馈功率与储能功率,可通过对Pess数据进行筛选获得。
3.2 仿真结果
1)阈值调整效果
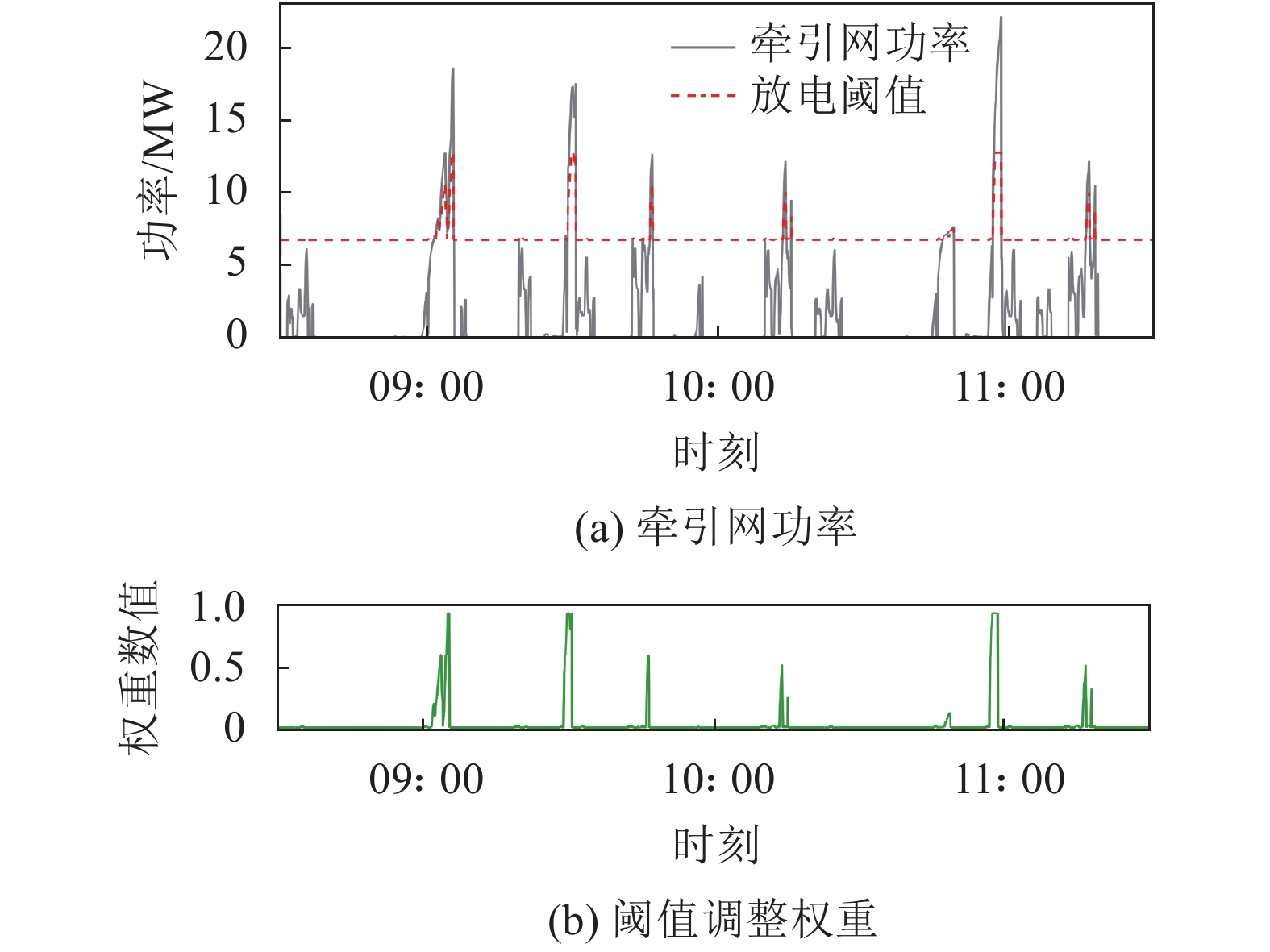
动态阈值的调整主要受外界牵引功率与ESS寿命两个因素的影响。一方面,由于牵引功率波动剧烈,可通过对放电阈值进行相应调整,从而降低牵引网的功率冲击及避免频繁地低功率放电,在较小的时间范围内可以观测到阈值的动态调整过程,该过程如图9所示。从图9可看出,随着牵引功率的波动,功率调整参数U经过FPN的推理,实现放电阈值在调整范围内动态变化。
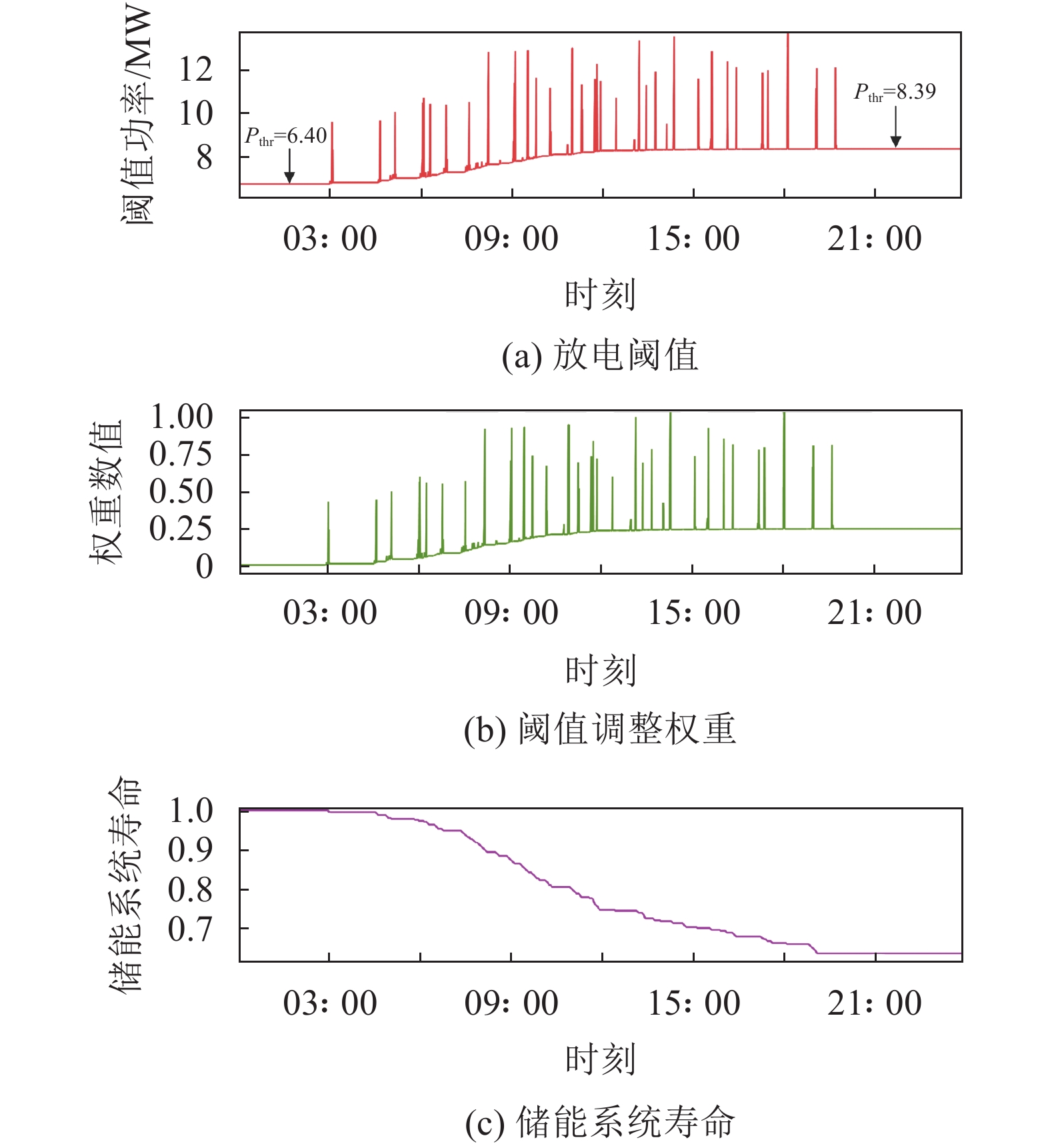
另一方面,由于储能系统在长期运行下存在明显的寿命衰减,FPN需要对放电阈值进行相应抬升从而降低平均放电深度,但由于储能系统寿命衰减缓慢,在单日的时间尺度下难以观测到寿命对放电阈值的影响。因此本文将储能系统寿命衰减速度进行提升以模拟500 d连续运行所带来的寿命衰减,结果如图10所示。根据图10可看出,随着寿命的快速衰减,阈值调整权重逐渐增加,使得放电阈值基准值由6.40 MW逐步提升至8.39 MW以降低储能系统的放电频率,从而延长储能系统寿命。
2)功率输出特性
为验证复杂工况下的储能系统与光伏发电系统配合的有效性,需要分析在正常寿命衰减速率下的短时功率输出,结果如图11所示。由图11的储能系统功率输出曲线可知,仅当牵引功率大于可变放电阈值时,储能系统会进行相应放电,并与光伏系统进行配合输出,降低牵引能耗16.514%。当列车处于再生制动状态时,储能系统会积极吸收再生制动能量,利用效率可达58.134%。
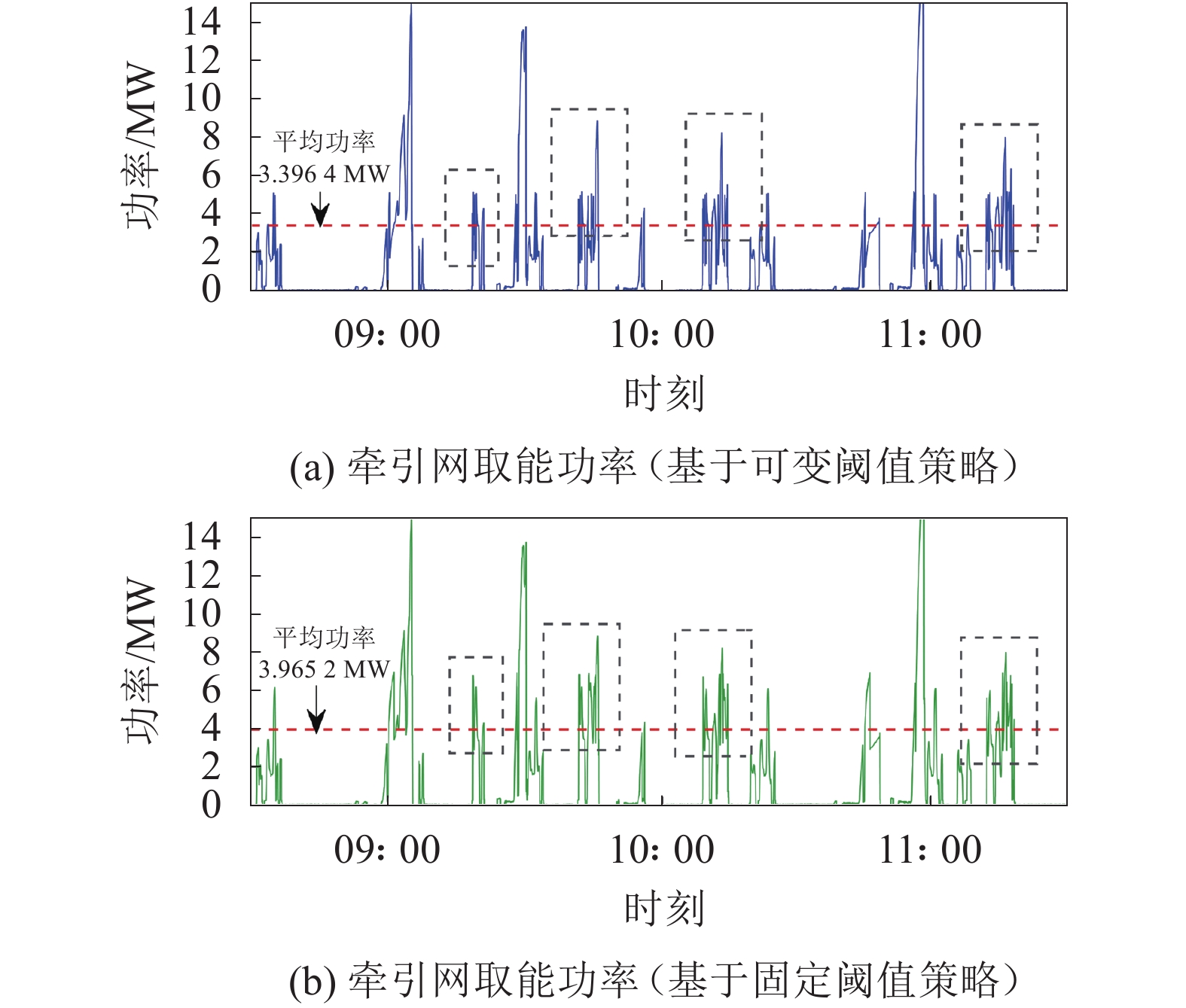
同时,由于动态阈值的引入,使得更多储存电能可运用于峰值功率的削减中,牵引网取能功率如图12所示。由图12可知,相较于固定阈值策略,基于FPN的可变阈值策略中电力机车经由接触网从电力系统取能的平均功率由3.965 MW下降至3.396 MW,降幅为14.3%。
与固定阈值策略相比,基于FPN的可变阈值策略由于采用了更加精准的放电策略,提升了光伏系统的能量利用效率,使得该策略在储能与能馈效率上具有明显优势,不同能量管理策略的汇总结果如表4所示。需要注意的是,由于储能系统能馈功率仍远低于峰值牵引功率,仅依靠能量的优化分配也不足以降低峰值功率,需要进一步提升储能系统输出功率与光伏系统装机容量。
表 4 不同能量管理策略结果对比Table 4 Comparison of results of different energy management strategies参 数 固定阈值策略 可变阈值策略 能馈效率/% 8.621 16.514 储能效率/% 43.311 58.134 ESS能馈电度/kWh 1 764.348 3 384.228 储能电度(再生)/kWh 2 073.835 2 783.598 储能电度(光伏、再生)/kWh 2 243.789 3 098.713 光伏发电利用电度/kWh 1 570.211 2 562.334 牵引网平均取能功率/MW 3.965 3.396 牵引网峰值取能功率/MW 18.007 18.007 储能系统在运行中需要削峰填谷及消纳可再生能源,但由于储能系统容量有限,且牵引网功率波动更为剧烈,运行工况更加复杂,因此,基于FPN的可变阈值策略给予削峰填谷功能更高优先度,以减少牵引网的功率波动,同时,采取更积极的放电策略,尽可能提升可再生能源利用效率。
3)寿命衰减特性
由于储能系统寿命存在对放电阈值的长期影响,因此需要从短期和长期两个尺度对寿命衰减进行分析。以单日寿命衰减为例,由于基于FPN的可变阈值策略采取了更加积极的放电策略,在放电次数、平均区间放电深度上均高于固定阈值策略,使得储能系统能馈效率提升92.02%(图4),但也相应增大了短时寿命损失,相应参数如表5所示。
表 5 短期寿命损失参数Table 5 Short term loss of life parameters参 数 固定阈值
策略可变阈值
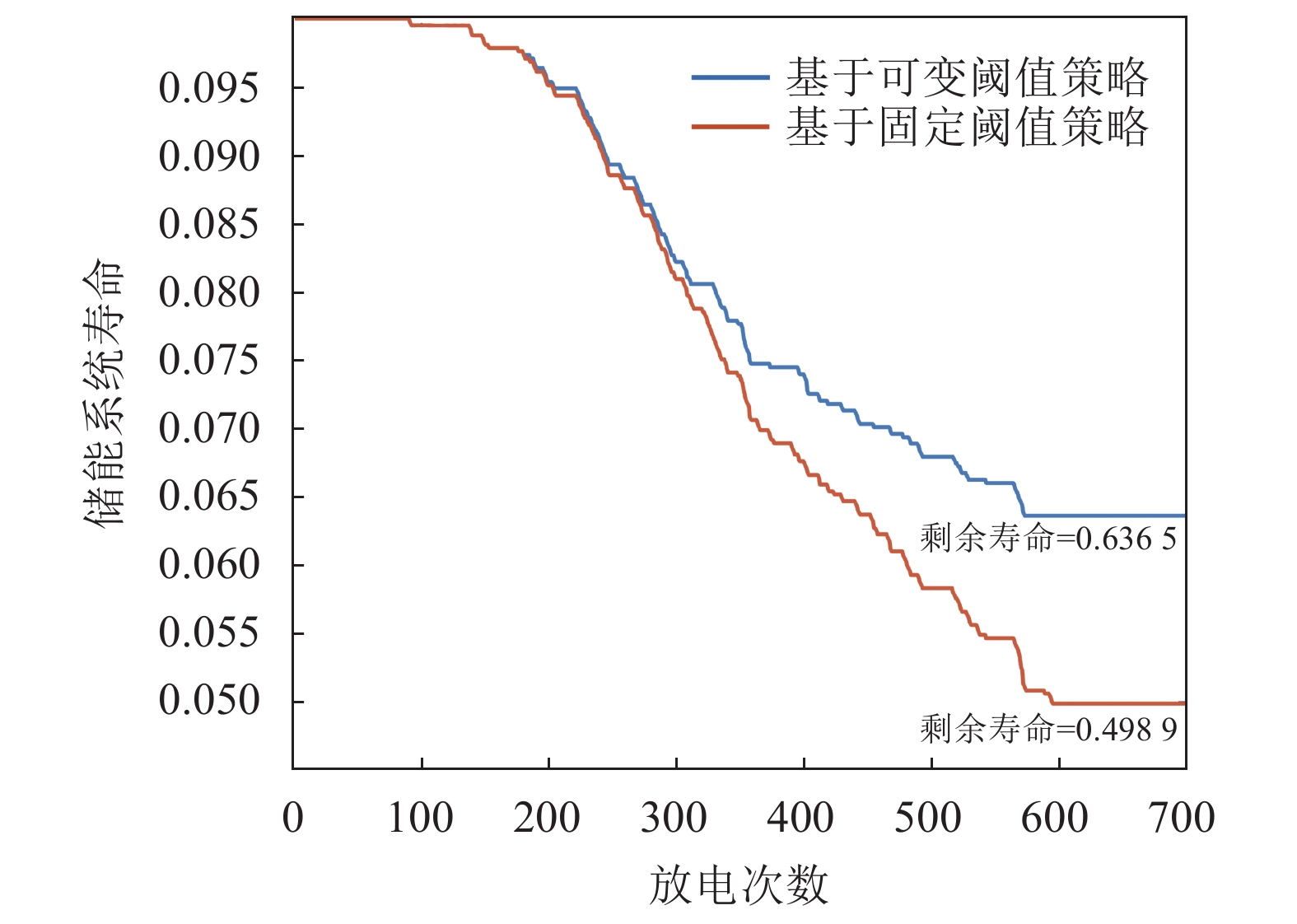
策略平均放电深度 0.021 0 0.023 0 平均荷电状态 0.724 0.608 平均放电频率 1.019 1.059 循环总次数 187 267 ESS剩余寿命/% 99.900 99.842 ESS寿命损失/% 0.100 0.158 从长期时间尺度来看,随着储能系统寿命的衰减,FPN网络会相应提升动态放电阈值以延长储能系统寿命,其长期寿命损失如图13所示。
由图13可知,随着放电次数增加,基于FPN的可变阈值策略的寿命衰减速度逐步减缓。该策略通过提升放电阈值降低单位采样区间的平均放电深度,达到延长储能系统寿命的效果。
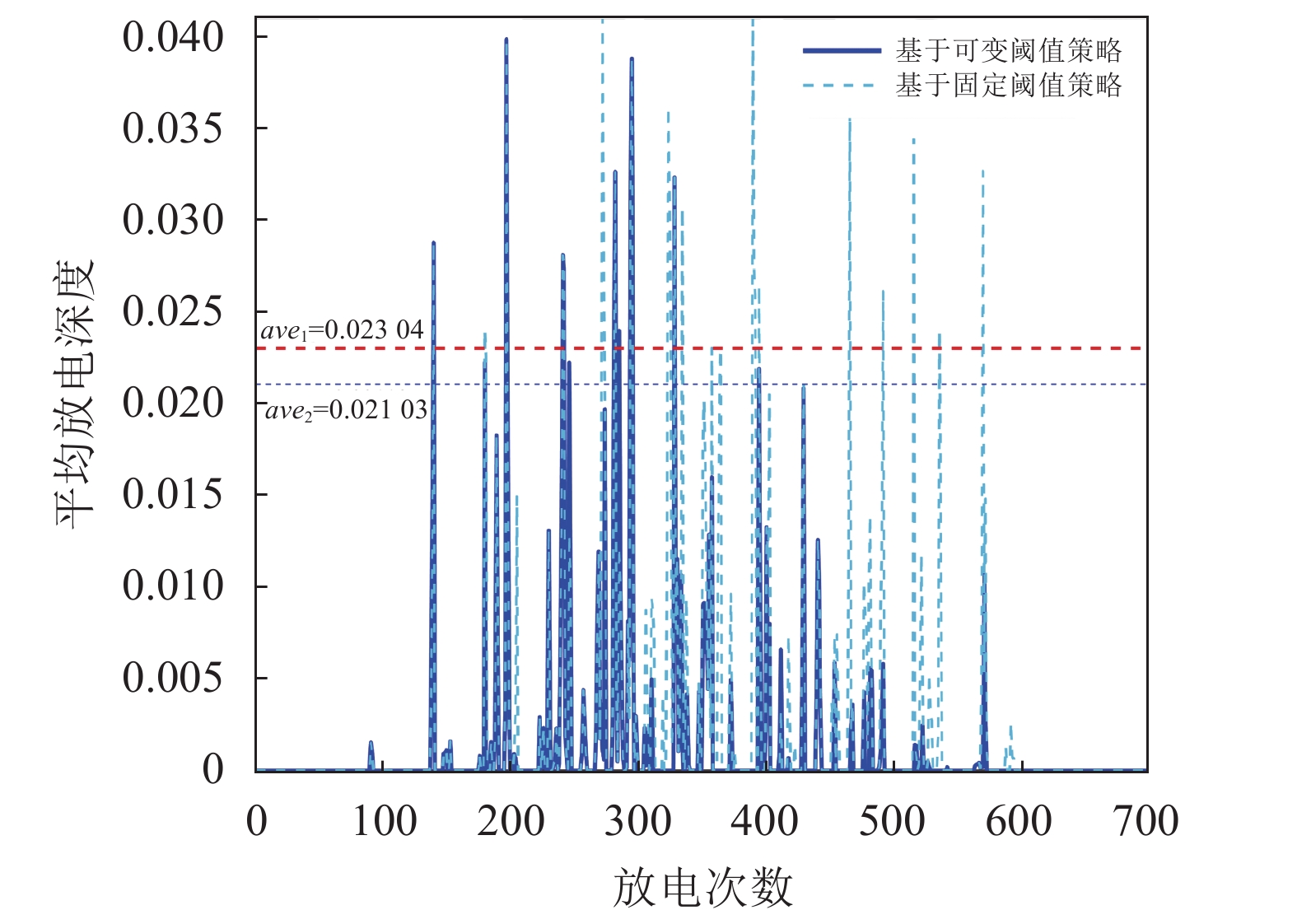
放电深度如图14所示。图14中,ave1为基于可变阈值策略的单位采样区间平均放电深度,ave2为基于固定阈值策略的单位采样区间平均放电深度。相较于固定阈值策略,基于FPN的可变阈值策略的平均放电深度有所降低。
表6为长期寿命损失仿真结果汇总,结果显示,经过500 d模拟放电后,基于固定阈值方案的ESS寿命损失是基于FPN动态阈值策略的137.86%,基于FPN的动态阈值策略有效降低了寿命损失。
表 6 长期寿命损失参数Table 6 Long term loss of life parameters参 数 固定阈值策略 可变阈值策略 ESS剩余寿命/% 49.890 63.652 ESS寿命损失/% 50.110 36.348 每计数间隔寿命损失/10–4 34.799 25.242 4. 结 论
本文提出了一种基于FPN的“网–源–储–车”动态阈值能量管理策略,在基本运行策略的基础上,该能量管理策略以牵引功率与储能系统寿命作为基本参数,经过模糊化、FPN推理、合并结果、反模糊化操作后,实现阈值的动态调整,并通过数值仿真对该策略进行验证,其主要结论如下:
1)该策略可以提升储能系统与光伏系统的调度积极性,有效提升储能系统储能与能馈效率,同时降低弃光现象的发生。
2)该策略能根据牵引功率实现储存电能的优化分配,降低电力机车经由牵引网从电力系统取能的平均功率。
3)该策略能够根据寿命衰减逐步提升动态放电阈值,降低平均放电深度,从而有效延长储能系统使用寿命。
然而,该策略主要平抑牵引负荷波动,仅将新能源发电系统作为储能系统的能量补充,从而造成一定的能量损失,因此,下一步研究还可考虑如何平抑源–荷双向波动性,提高可再生能源利用率;同时,由于该策略依赖当前状态下的系统功率参数,可结合各类列车功率预测算法[29],提升FPN系统的响应速度与准确性;此外,该策略还可适应不同架构的“网–源–储–车”协同供能系统,通过修改变换器控制系统,可适用于多种应用场景。
-
表 1 多工况功率分配
Table 1 Multi-condition power distribution
列车工况 功率平衡方程 基本判据 牵引 $ {P}_{\text{tr} }={P}_{\text{po} }-{P}_{\text{loss} } $,
${P}_{\text{ess} }={P}_{\text{ev} }(储能系统充电) $牵引功率小于阈值 ${P_{ {{\rm{tr}}} } } = {P_{ {{\rm{ess}}} } } + {P_{ {{\rm{ev}}} } } + {P_{ {{\rm{po}}} } } - {P_{ {{\rm{loss}}} } }$ 牵引功率大于阈值 ${P}_{\text{tr} }={P}_{\text{po} }-{P}_{\text{loss} }$,
${P}_{\text{ess} }={P}_{\text{ev} }(储能系统充电) $牵引功率大于阈值,
SSOC越限再生制动 ${P_{ {{\rm{re}}} } } = {P_{ {{\rm{ess}}} } } - {P_{ {{\rm{ev}}} } } + {P_{ {{\rm{po}}} } } + {P_{ {{\rm{loss}}} } }$ SSOC
未越限$ {P_{ { {\rm{re} } } } } = {P_{ { {\rm{po} } } } } + {P_{ { {\rm{loss} } } } } $,
${ {P_{ { {\rm{ess} } } } } = {P_{ { {\rm{ev} } } } } = 0 \qquad }$SSOC
越限惰行/空闲 ${P}_{\text{re} }={P}_{\text{po} }=0$,
$ {P}_{\text{ess} }={P}_{\text{ev} }(储能系统充电) $SSOC
未越限${P_{ { {\rm{re} } } } } = {P_{ { {\rm{po} } } } } = 0$,
$ {P_{ { {\rm{ess} } } } } = {P_{ { {\rm{ev} } } } } = 0 $SSOC
越限表 2 阈值调整模糊规则
Table 2 Threshold adjustment fuzzy rules
牵引功率P 阈值调整参数U 寿命 L=S 寿命 L=M 寿命 L=L SS SS SS S S SS S M M S M L L M L LL LL L LL LL 表 3 系统基本参数
Table 3 System basic parameters
系统参数 数值 ESS额定功率/MW 3.2 ESS额定容量/kWh 331.2 ESS荷电状态范围 (0.25,0.85) 光伏发电装机容量/MW 2.0 固定放电阈值/MW 7.0 放电阈值基准值/MW 6.4 放电阈值波动范围/MW 6.4 牵引能量总电度/kWh 20 943.3 再生制动能量总电度/kWh 4 788.2 表 4 不同能量管理策略结果对比
Table 4 Comparison of results of different energy management strategies
参 数 固定阈值策略 可变阈值策略 能馈效率/% 8.621 16.514 储能效率/% 43.311 58.134 ESS能馈电度/kWh 1 764.348 3 384.228 储能电度(再生)/kWh 2 073.835 2 783.598 储能电度(光伏、再生)/kWh 2 243.789 3 098.713 光伏发电利用电度/kWh 1 570.211 2 562.334 牵引网平均取能功率/MW 3.965 3.396 牵引网峰值取能功率/MW 18.007 18.007 表 5 短期寿命损失参数
Table 5 Short term loss of life parameters
参 数 固定阈值
策略可变阈值
策略平均放电深度 0.021 0 0.023 0 平均荷电状态 0.724 0.608 平均放电频率 1.019 1.059 循环总次数 187 267 ESS剩余寿命/% 99.900 99.842 ESS寿命损失/% 0.100 0.158 表 6 长期寿命损失参数
Table 6 Long term loss of life parameters
参 数 固定阈值策略 可变阈值策略 ESS剩余寿命/% 49.890 63.652 ESS寿命损失/% 50.110 36.348 每计数间隔寿命损失/10–4 34.799 25.242 -
[1] 中国国家铁路集团有限公司.中国国家铁路集团有限公司2021年统计公报[R].北京:中国国家铁路集团有限公司,2022. [2] 胡海涛,郑政,何正友,等.交通能源互联网体系架构及关键技术[J].中国电机工程学报,2018,38(1):12–24. doi: 10.13334/j.0258-8013.pcsee.171969 Hu Haitao,Zheng Zheng,He Zhengyou,et al.The framework and key technologies of traffic energy Internet[J].Proceedings of the CSEE,2018,38(1):12–24 doi: 10.13334/j.0258-8013.pcsee.171969 [3] 韦晓广,高仕斌,臧天磊,等.社会能源互联网:概念、架构和展望[J].中国电机工程学报,2018,38(17):4969–4986. doi: 10.13334/j.0258-8013.pcsee.180846 Wei Xiaoguang,Gao Shibin,Zang Tianlei,et al.Social energy Internet:Concept,architecture and outlook[J].Proceedings of the CSEE,2018,38(17):4969–4986 doi: 10.13334/j.0258-8013.pcsee.180846 [4] 何正友,向悦萍,廖凯,等.能源–交通–信息三网融合发展的需求、形态及关键技术[J].电力系统自动化,2021,45(16):73–86. doi: 10.7500/AEPS20210312006 He Zhengyou,Xiang Yueping,Liao Kai,et al.Demand,form and key technologies of integrated development of energy–transport–information networks[J].Automation of Electric Power Systems,2021,45(16):73–86 doi: 10.7500/AEPS20210312006 [5] 罗嘉明,韦晓广,高仕斌,等.高速铁路储能系统容量配置与能量管理技术综述与展望[J/OL].中国电机工程学报[2022 –03–23].http://www.pcsee.org/CN/abstract/abstract34276.shtml. Luo Jiaming,Wei Xiaoguang,Gao Shibin,et al.Summary and outlook of capacity configuration and energy management technology of high-speed railway energy storage system[J/OL].Proceedings of the CSEE[2022–03–23].http://www.pcsee.org/CN/abstract/abstract34276.shtml. [6] 王玙,杨中平,李峰,等.有轨电车混合动力系统能量交互型管理策略与容量配置协同优化研究[J].电工技术学报,2019,34(8):1780–1788. doi: 10.19595/j.cnki.1000-6753.tces.180552 Wang Yu,Yang Zhongping,Li Feng,et al.Energy management strategy with energy interaction and configuration optimization for the tram’s hybrid storage system[J].Transactions of China Electrotechnical Society,2019,34(8):1780–1788 doi: 10.19595/j.cnki.1000-6753.tces.180552 [7] Teleke S,Baran M E,Bhattacharya S,et al.Rule-based control of battery energy storage for dispatching intermittent renewable sources[J].IEEE Transactions on Sustainable Energy,2010,1(3):117–124. doi: 10.1109/TSTE.2010.2061880 [8] 马茜,郭昕,罗培,等.基于超级电容储能的新型铁路功率调节器协调控制策略设计[J].电工技术学报,2019,34(4):765–776. doi: 10.19595/j.cnki.1000-6753.tces.180095 Ma Qian,Guo Xin,Luo Pei,et al.Coordinated control strategy design of new type railway power regulator based on super capacitor energy storage[J].Transactions of China Electrotechnical Society,2019,34(4):765–776 doi: 10.19595/j.cnki.1000-6753.tces.180095 [9] 黄小红,赵艺,李群湛,等.电气化铁路同相储能供电技术[J].西南交通大学学报,2020,55(4):856–864. doi: 10.3969/j.issn.0258-2724.20181083 Huang Xiaohong,Zhao Yi,Li Qunzhan,et al.Co-phase traction power supply and energy storage technology for electrified railway[J].Journal of Southwest Jiaotong University,2020,55(4):856–864 doi: 10.3969/j.issn.0258-2724.20181083 [10] 鲍冠南,陆超,袁志昌,等.基于动态规划的电池储能系统削峰填谷实时优化[J].电力系统自动化,2012,36(12):11–16. Bao Guannan,Lu Chao,Yuan Zhichang,et al.Load shift real-time optimization strategy of battery energy storage system based on dynamic programming[J].Automation of Electric Power Systems,2012,36(12):11–16 [11] Gao Zongyu,Fang Jianjun,Zhang Yinong,et al.Control strategy for wayside supercapacitor energy storage system in railway transit network[J].Journal of Modern Power Systems and Clean Energy,2014,2(2):181–190. doi: 10.1007/s40565-014-0060-4 [12] Yang Zhihong,Yang Zhongping,Li Xuyang,et al.The real-time optimization of charge/discharge voltage threshold for energy storage system in urban rail transit[C]//Proceedings of the IECON 2017-43rd Annual Conference of the IEEE Industrial Electronics Society.Beijing:IEEE,2017:3930–3935. [13] 胡海涛,陈俊宇,葛银波,等.高速铁路再生制动能量储存与利用技术研究[J].中国电机工程学报,2020,40(1):246–256. Hu Haitao,Chen Junyu,Ge Yinbo,et al.Research on regenerative braking energy storage and utilization technology for high-speed railways[J].Proceedings of the CSEE,2020,40(1):246–256 [14] 邓文丽,戴朝华,韩春白雪,等.计及再生制动能量回收和电能质量改善的铁路背靠背混合储能系统及其控制方法[J].中国电机工程学报,2019,39(10):2914–2924. doi: 10.13334/j.0258-8013.pcsee.181069 Deng Wenli,Dai Chaohua,Han Chunbaixue,et al.Back-to-back hybrid energy storage system of electric railway and its control method considering regenerative braking energy recovery and power quality improvement[J].Proceedings of the CSEE,2019,39(10):2914–2924 doi: 10.13334/j.0258-8013.pcsee.181069 [15] 陈霖华,陈剑,徐志强,等.基于实时电路模型的储能系统锂离子电池状态估算[J].中南大学学报(自然科学版),2021,52(2):458–464. Chen Linhua,Chen Jian,Xu Zhiqiang,et al.State estimation of lithium ion battery in energy storage system based on real time circuit model[J].Journal of Central South University (Science and Technology),2021,52(2):458–464 [16] 吴春芳.动力电池SOC估算综述[J].电源技术,2017,41(12):1795–1798. doi: 10.3969/j.issn.1002-087X.2017.12.039 Wu Chunfang.Review of state of charge estimation for power battery[J].Chinese Journal of Power Sources,2017,41(12):1795–1798 doi: 10.3969/j.issn.1002-087X.2017.12.039 [17] 诸斐琴,杨中平,林飞,等.基于加速时间预测的现代有轨电车储能系统能量管理与容量配置优化研究[J].电工技术学报,2017,32(23):158–166. Zhu Feiqin,Yang Zhongping,Lin Fei,et al.Research on acceleration-time-prediction-based energy management and optimal sizing of onboard energy storage system for modern trams[J].Transactions of China Electrotechnical Society,2017,32(23):158–166 [18] 杨浩丰,刘冲,李彬,等.基于列车运行工况的城轨地面式混合储能系统控制策略研究[J].电工技术学报,2021,36(增刊1):168–178. Yang Haofeng,Liu Chong,Li Bin,et al.Research on control strategy of urban rail ground hybrid energy storage device based on train operating condition[J].Transactions of China Electrotechnical Society,2021,36(Supp1):168–178 [19] 王青元,冯晓云,朱金陵,等.考虑再生制动能量利用的高速列车节能最优控制仿真研究[J].中国铁道科学,2015,36(1):96–103. doi: 10.3969/j.issn.1001-4632.2015.01.14 Wang Qingyuan,Feng Xiaoyun,Zhu Jinling,et al.Simulation study on optimal energy-efficient control of high speed train considering regenerative brake energy[J].China Railway Science,2015,36(1):96–103 doi: 10.3969/j.issn.1001-4632.2015.01.14 [20] 刘宇嫣,杨中平,林飞,等.城轨地面式混合储能系统自适应能量管理与容量优化配置研究[J].电工技术学报,2021,36(23):4874–4884. doi: 10.19595/j.cnki.1000-6753.tces.210853 Liu Yuyan,Yang Zhongping,Lin Fei,et al.Study on adaptive energy management and optimal capacity configuration of urban rail ground hybrid energy storage system[J].Transactions of China Electrotechnical Society,2021,36(23):4874–4884 doi: 10.19595/j.cnki.1000-6753.tces.210853 [21] 刘畅,卓建坤,赵东明,等.利用储能系统实现可再生能源微电网灵活安全运行的研究综述[J].中国电机工程学报,2020,40(1):1–18. Liu Chang,Zhuo Jiankun,Zhao Dongming,et al.A review on the utilization of energy storage system for the flexible and safe operation of renewable energy microgrids[J].Proceedings of the CSEE,2020,40(1):1–18 [22] 丁明,徐宁舟,毕锐,等.基于综合建模的3类电池储能电站性能对比分析[J].电力系统自动化,2011,35(15):34–39. Ding Ming,Xu Ningzhou,Bi Rui,et al.Modeling and comparative study on multiple battery energy storage systems[J].Automation of Electric Power Systems,2011,35(15):34–39 [23] 刘敦楠,王佳妮,华婧雯,等.基于模糊Petri网的能源互联网场景特征识别方法[J].电网技术,2020,44(10):3725–3734. Liu Dunnan,Wang Jiani,Hua Jingwen,et al.Feature identification method of energy Internet scene based on fuzzy Petri net[J].Power System Technology,2020,44(10):3725–3734 [24] 孟飞翔,雷英杰,余晓东,等.基于直觉模糊Petri网的知识表示和推理[J].电子学报,2016,44(1):77–86. doi: 10.3969/j.issn.0372-2112.2016.01.012 Meng Feixiang,Lei Yingjie,Yu Xiaodong,et al.Knowledge representation and reasoning using intuitionistic fuzzy Petri nets[J].Acta Electronica Sinica,2016,44(1):77–86 doi: 10.3969/j.issn.0372-2112.2016.01.012 [25] 胡海涛,葛银波,黄毅,等.电气化铁路“源–网–车–储”一体化供电技术[J].中国电机工程学报,2022,42(12):4374–4391. doi: 10.13334/J.0258-8013.PCSEE.210255 Hu Haitao,Ge Yinbo,Huang Yi,et al.“Source–network–train–storage” integrated power supply system for electric railways[J].Proceedings of the CSEE,2022,42(12):4374–4391 doi: 10.13334/J.0258-8013.PCSEE.210255 [26] 袁佳歆,曲锴,郑先锋,等.高速铁路混合储能系统容量优化研究[J].电工技术学报,2021,36(19):4161–4169. Yuan Jiaxin,Qu Kai,Zheng Xianfeng,et al.Optimizing research on hybrid energy storage system of high speed railway[J].Transactions of China Electrotechnical Society,2021,36(19):4161–4169 [27] 韩晓娟,程成,籍天明,等.计及电池使用寿命的混合储能系统容量优化模型[J].中国电机工程学报,2013,33(34):91–97. doi: 10.13334/j.0258-8013.pcsee.2013.34.015 Han Xiaojuan,Cheng Cheng,Ji Tianming,et al.Capacity optimal modeling of hybrid energy storage systems considering battery life[J].Proceedings of the CSEE,2013,33(34):91–97 doi: 10.13334/j.0258-8013.pcsee.2013.34.015 [28] 杨健维,何正友,臧天磊.基于方向性加权模糊Petri网的电网故障诊断方法[J].中国电机工程学报,2010,30(34):42–49. doi: 10.13334/j.0258-8013.pcsee.2010.34.005 Yang Jianwei,He Zhengyou,Zang Tianlei.Power system fault-diagnosis method based on directional weighted fuzzy Petri nets[J].Proceedings of the CSEE,2010,30(34):42–49 doi: 10.13334/j.0258-8013.pcsee.2010.34.005 [29] 魏波,胡海涛,王科,等.基于实测数据和行车运行图的高铁牵引变电站负荷预测方法[J].电工技术学报,2020,35(1):179–188. doi: 10.19595/j.cnki.1000-6753.tces.181892 Wei Bo,Hu Haitao,Wang Ke,et al.Research on traction load forecasting method for high-speed railway traction substation based on measured data and train timetable[J].Transactions of China Electrotechnical Society,2020,35(1):179–188 doi: 10.19595/j.cnki.1000-6753.tces.181892


 下载:
下载: